中国数学问题提出能力培养的发展路径与启示

李沐慧徐斌艳

中国数学问题提出能力培养的发展路径与启示

李沐慧1，徐斌艳1，2

（1．华东师范大学 教师教育学院，上海 200062；2．华东师范大学 课程与教学研究所，上海 200062）

当下中国基础教育正值深化改革之际，培养创新型人才不可空言无补，从学科入手，从基础抓起，培养学生问题提出能力是关键．分析20世纪以来中小学数学课程纲领性文件，得出中国培养学生问题提出能力的发展路径分为3个阶段：1902—1977年教学方法层面的酝酿萌生期，1978—2000年目标驱动之下的初步探索期，2001—2018年自上而下式统筹的稳步发展期．结合研究结果，得出培养学生问题提出能力的基本经验与启示有：保护低龄儿童提问意识，逐步推进提问能力发展；创设多样提问教学情境，运用策略揭示提问过程；深度剖析提问思维本质，推进问题提出评价研究．

数学课程；问题提出；能力培养；发展路径

1 问题提出

问题对学科发展而言至关重要，培养学生问题提出能力是社会对教育创新的迫切需求．一百年前的巴黎数学家大会上，著名的“希尔伯特23问”引领了超过一个世纪的数学学科发展，其中仍有许多问题至今令人殚心竭虑．希尔伯特说：“只要一门科学分支充满着大量问题，它就充满生命力．缺少问题则意味着死亡或者独立发展的终止．”[1]1938年，爱因斯坦在《物理学的进化》中也指出：“提出一个问题往往比解决一个问题更重要……提出新的问题……需要有创造性的想象力，而且标志着科学的真正进步．”[2]20世纪80年代初，全美数学教师理事会（NCTM）在美国乃至世界范围内掀起了以“问题解决”为核心的数学教育改革，人们在反思其后的10年教学实践中发现“不关注问题的产生和表达会制约学生的数学思维发展”[3]．自此，“问题提出”开始作为相对独立的数学活动为数学教育界所研究．NCTM在《学校数学课程与评价标准》（1989）中提出了增加“问题提出”活动的教学要求，指出教师在课堂教学中应重视学生提出数学问题的活动，提供学生从给定情境中提出问题的机会[4]．20世纪90年代，随着教育改革的推进和知识经济社会的发展，中国数学教育界开始了有关学生问题提出能力培养的研究[5]．研究发现，“问题提出”除了能够训练学生的数学推理等能力，对激发数学学习兴趣、创造力，提升交流表达能力，培养合作学习能力都大有裨益[6]．

课程文件是指导教材编写、课程实施的基础，是教学变革的有力表征．因此，探究学生数学问题提出能力的培养与发展，课程文件是最初始也是最根本的研究切入点之一．然而，现有的数学问题提出文本类研究大多集中在教材编写的比较层面，很少实质性探究教材如何包含问题提出[7]．例如，在哪些数学内容教学中适合渗透问题提出，以及如何评价数学教材与课程标准关于问题提出能力要求是否一致等，这些问题都使得对数学课程文件的分析研究尤为必要．其实，随着研究的不断深入，中国数学课程文件对“问题提出”的教学要求已经愈加细化具体．2001年，《全日制义务教育数学课程标准（实验稿）》分学段对“问题提出”教学提出了相应的具体目标．例如，要求一～三年级的学生“能在教师的指导下，从日常生活中发现和提出简单的数学问题，并尝试解决”[8]．《义务教育数学课程标准》（2011年版）和《普通高中数学课程标准》（2017年版）明确提出要增强学生“发现和提出问题的能力、分析和解决问题的能力”[9–10]．即便如此，最新研究发现，学生的问题提出能力仍存在地区差异和提升空间[11]．对中国数学教育研究者而言，问题提出一直以舶来品的身份在国内数学教育研究中发展，而分析百年来的课程文件，能够发现中国数学问题提出教育的本源所在，立足于“编题”“变式”等中国数学教育特色，是培养中国学生问题提出能力的既有基础与实践抓手．创新始于问题，学生缺乏问题意识、提不出高质量问题的现象再无改观，创新型人才培养则如无源之水、无本之木．为此，研究者尝试从数学课程文件出发，探索中国学生数学问题提出能力培养的发展路径，结合业内学者对当下数学问题提出现状的评价，为未来中国学生问题提出能力培养提供新的启示．

2 研究设计

2.1 研究对象

研究问题1的样本为中国20世纪以来官方发布的34个数学课程纲领性文件，包括数学课程标准、教学大纲等．它们对当时的数学教材编写、课程实施等有指导性作用，具体如表1所示．

表1 研究对象

研究问题2的参与者为10位国内数学教育领域的学者．为挖掘课程标准研制、编写、使用过程背后的故事，更加全面、客观地分析义务教育阶段和高中教育阶段培养学生问题提出能力的实际状况与困境，加深对课程文件的理解认识，研究采用半结构、一对一的方式，深度访谈了4位高校数学教育学者、3位数学特级教师、2位数学教研员和1位数学教材编委（具体受访人员作虚拟化处理）．

2.2 研究问题

（1）1902年来中国数学课程文件中学生“数学问题提出能力”的内涵演变呈现出怎样的特点？具体要求发生了怎样的变化？

（2）如何解读课程要求下中国数学问题提出教育的现状与未来？

2.3 研究方法

研究选取内容分析法作为问题1的主要研究方法．内容分析是对书面资料进行总结和报告的过程，即抽取书面资料和信息的核心内容．严格来讲，它是对书面资料的内容进行系统分析、检验和验证的过程[14]．其次，参考泰勒课程原理设计编码框架[15]，对所有课程文件进行筛选编码并完成一致性检验，得到共计113个问题提出的有效词条，研究流程如图1所示．

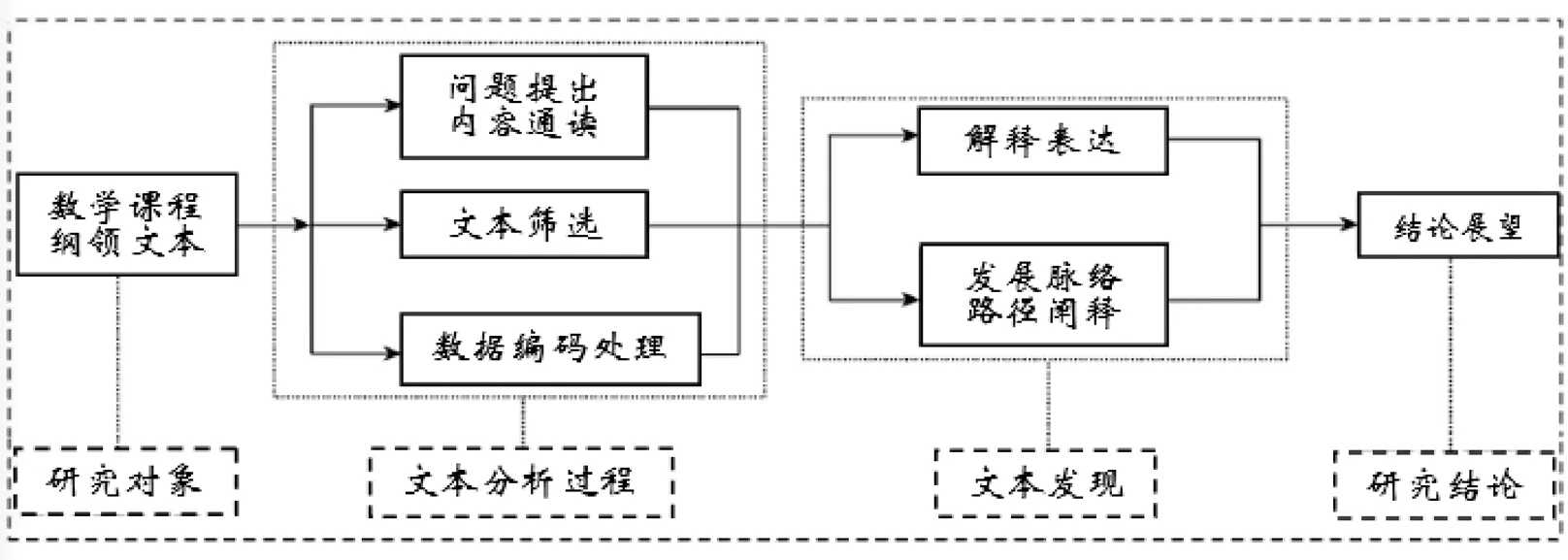
图1 问题1研究流程

研究问题2所涉及的访谈主要围绕问题提出以下3方面（6个问题）展开：内涵与价值、发展与评价、培养与困境．同时，针对受访者不同的身份特征，设计了部分针对性问题．研究分析了访谈文本中的关键词和主要观点，阐述国内数学教育领域围绕“问题提出能力培养”的代表性思想，访谈提纲详见表2．

表2 访谈提纲

3 研究结果

3.1 问题提出能力培养的发展路径

19世纪90年代，中国正值动荡的清末时期．在此期间，数学课程内容与形式上的新旧交替将中国近代数学教育推向了一个又一个高潮．1949年以后，中国又经历了多次数学教育改革，包括学习苏联时期、教育大革命时期、调整提高时期、“文革”时期、巩固发展时期、全面改革时期[16]．随着课程体系的日渐完善，以学生为本，以逻辑为序等兼具人性化和科学化的课程特征愈加鲜明．参考有关中国数学教育发展的史料文献，结合编码分析和解释性分析（如图2所示）．研究得出：1902—2018年，中国数学课程文件中关于学生问题提出培养可划分为以下3个阶段．

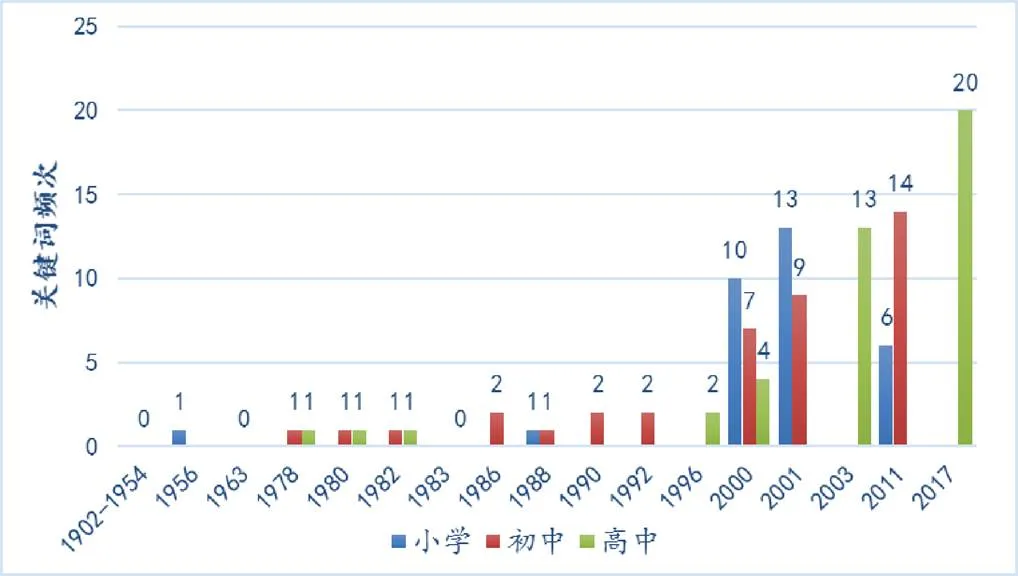
图2 各个学段课程文件中“问题提出”关键词频

（1）1902—1977年：教学方法层面的酝酿萌生期．

从数据看，1902—1977年间中国数学课程对“问题提出”几乎没有任何关注，仅在1956年《小学算术教学大纲（修订草案）》的教学指示中出现过1次，具体表述为：“在算术教学中可以利用小学历史、地理、自然等科目里的材料，把它们编成应用题让儿童解答……还必须使儿童逐渐练习自己编一些类似在课堂上解答过的应用题．”[12]可见，“编题”是早期教育文件中对问题提出的理解，这与台湾地区学者采用的“拟题”“布题”等措辞相近，但与西方学者的表述略有不同．20世纪末，从西方兴起的数学问题提出教育研究采用的是“problem formulation”“problem finding”“problem generation”等词[17]，与中国以“题目”为目标的操作性导向不同，以上英文词源更多地体现了提问行为过程与创新发现的重要性．

从语义分析，1956年大纲中的这一教学指示虽然将儿童提问局限于仿照编应用题的简单层面，却是首次关注到了提问从教师主体向学生主体的转变，并且强调用跨学科素材提问，以实现数学知识的灵活应用．波利亚归纳了教师提问的基本方法：从一个普通而自然的问题开始，逐渐深入到更加特殊和具体的问题，引发学生的思维反应[18]．实践中，优秀的中国数学教师已经将类似的编题思路和方法运用得炉火纯青，而大纲要求让学生练习模拟教师编题，实则是要求教师恰当地展现自己编题时的思维方法．用弗赖登塔尔的话说，与其说让学生学习数学，不如说让学生学习数学化，即数学地组织现实世界的过程[19]．可惜在后续的三十多年中，这条单薄却具有突破性的教学指示没有得到重视与发展，淹没在文海之中，此谓教学方法层面上的酝酿萌生．

（2）1978—2000年：目标驱动之下的初步探索期．

统计显示，1978—1999年“问题提出”如星星之火般零散分布于课程文件，且表述多为一句带过，并无详细解读．其中，小学课程文件中的相关词频仅为1，初、高中课程文件中分别为10和5，且相邻年份的课程文件在排版表述上没有什么变化与新意．2000年，中国数学课程全面改革拉开序幕，很多探索性工作已经完成．在2000年的小、初、高3本数学课程大纲中，“问题提出”有关内容体现多达21处，其中特别注重培养小学生从生活实践中发现问题的能力．

排版分布上，研究对这一时期“问题提出”内容在文件中的“地理位置”进行了分析，得出1978—2000年、2001—2018年两个时间段的分布图（如图3所示）．可见，不同时期课程文件中“问题提出”涉及的层面不同．1978—2000年的课程文件在“目标、内容、方法”3个方面涉及了学生问题提出能力的培养．所有表述中，以内容和方法为主，分别占据了48.6%和40.5%．

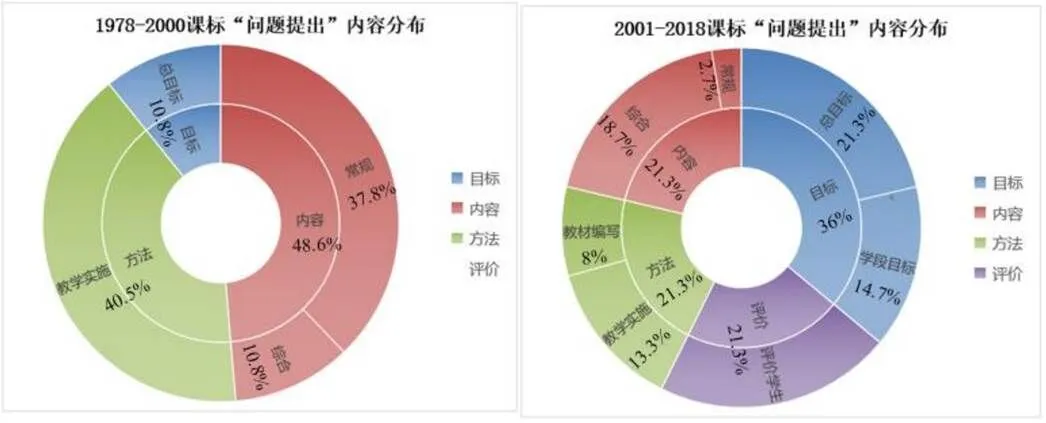
图3 “问题提出”排版分布

就内容而言，这一时期的6部大纲就问题提出内容的编写呈现“爬楼梯”与“下基层”的双重走势．培养要求的级别从教学注意点上升为教学目标，加之表述方式的更新繁复，此为“爬楼梯”．后阶段大纲在前者基础上，结合具体教学内容，提出“类比法”等操作层面的具体培养手段，此为“下基层”，这为培养学生数学问题提出能力自上而下地落实提供了有效指导．1978年大纲在教学注意点中首次提及了“发现问题—提出问题—解决问题”的学生能力链式培养思路[12]．1982年大纲提出培养学生把实际问题转化为数学问题并加以合理解决的能力．自此，“将实际问题数学化”成为课程培养学生问题提出能力的重要目标．在此基础上，后续大纲就具体的数学知识点增添了有关要求．1988年、1992年、2000年3部初中教学大纲也前呼后应，贯彻“坚持理论联系实际”的思想，强调教学要从学生熟悉的生活、生产和其它学科的实际问题出发，进行科学抽象和逻辑推理，使学生受到把实际问题抽象成数学问题的训练．2000年大纲首次将“问题提出”与“创新意识和实践能力”挂钩，指出“在教学中要激发学生学习数学的好奇心和求知欲，通过独立思考，不断追求新知，发现、提出、分析并创造性地解决问题，使数学学习成为再发现、再创造的过程”[8]．

总的来说，这一时期的课程文件受实用主义教育理念影响，以“将实际问题抽象成数学问题”教学目标为导向，跳出了“提问即编题”的狭义内涵．同时，课程对问题提出的来源与质量也有所要求，并在教学实施中结合具体教学内容给予了教师案例指导，此谓目标驱动之下的初步探索．

（3）2001—2018年：自上而下统筹的稳步发展期．

这一时期的“问题提出”已经缓缓从帷幕中走出，正式亮相．2001年起，义务教育阶段和高中阶段课程标准分开编写，4本课程标准中“问题提出”相关词汇出现了18次以上，在2017年版高中标准更是达到20次．诚然，相较于浩如烟海的成千词句，这些词句数量还很少，但在惜字如金的课程标准中，每个词、每句话都体现了中国数学课程对“问题提出”教育价值的肯定与重视．因此研究通过解释性分析，列举了不同时期课程文件中与“问题提出”有关的核心概念、重要观点，得出结论如图4所示．

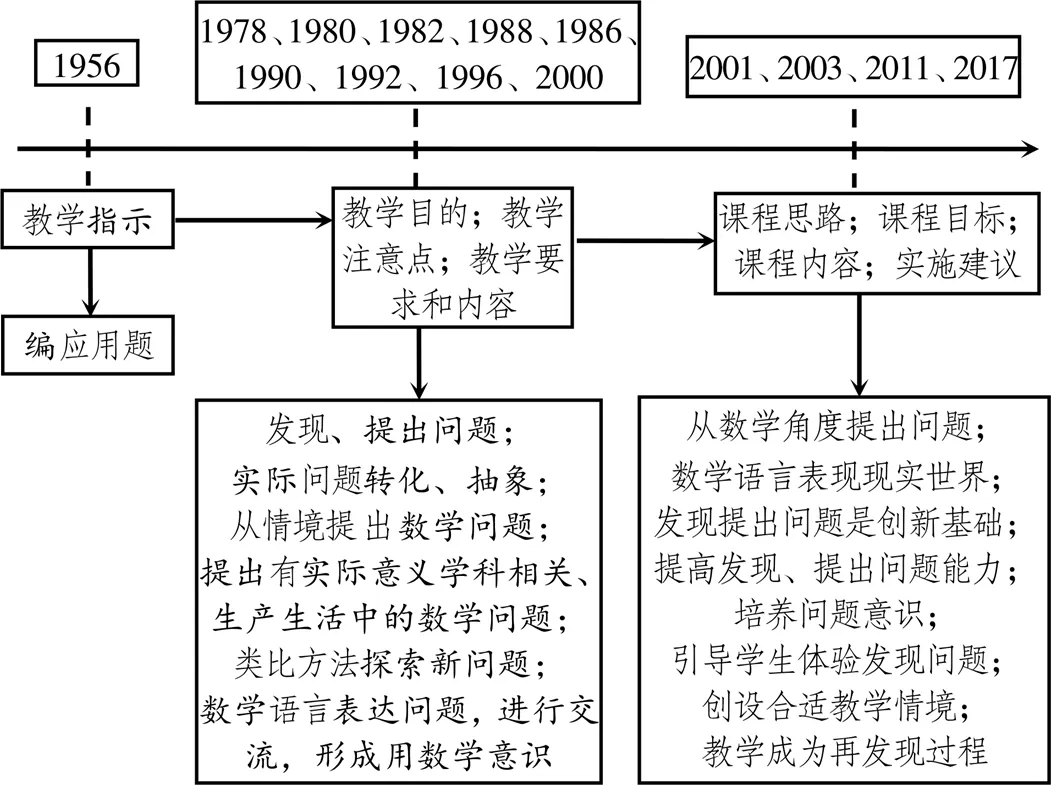
图4 “问题提出”内容变化发展

该时期“问题提出培养”已在课程的“目标、内容、方法、评价”4个方面均有体现，且比例相当，分别为36%、21%、22%、21%．在目标层面上，文件明确表述了要提高数学地提出、分析和解决问题（包括简单实际问题）的能力．就此，问题提出似乎与问题解决有并驾齐驱之势．在内容层面上，课程将培养学生问题提出的载体从常规课程转向数学探究、数学建模等多样的综合性课程．在方法层面上，课程强调教法的同时，还给出了教材编写意见，要求教材应注意创设情境，从实例出发，展现数学知识的发生、发展过程，使学生能够从中发现问题、提出问题．更重要的是，课程标准中明确给出了针对学生问题提出的评价建议，特别针对综合课程，要求教师应采取灵活的方式记录、保留和分析学生提出问题的表现．可惜，在重重目标和诸多建议的闪光灯下，课程标准并没有给出一个具体的评价实例，其操作指导力仍有待提升．

总的来说，此时期“问题提出培养”以能力为标杆，要求提高学生发现、提出问题的能力，从数学、生活等多角度提出问题．另外，课程文件还明确指出发现问题是创新的基础，需要超越操作层面培养学生的问题意识，为此教师需要引导学生体验发现问题，创设合适情境，将教学成为再发现的过程，此谓自上而下统筹的稳步发展．

3.2 课程要求下中国问题提出教育的现状与未来

通过访谈，学者们从内涵与价值、发展与现状、培养与困境等方面解读了课程要求下中国学生问题提出培养的教育现状及未来启示（如表3），分析访谈文本得出以下结论．

表3 访谈结果分析

3.2.1 内涵与价值

问题提出的内涵存在广义和狭义之争，10位学者中有5位接纳问题提出的广义内涵，1位认可狭义内涵，另4位无明确偏向．半数学者认为不仅从情境中提问，猜想、对教材知识的质疑等都属于提问范畴．譬如，学者G1认为问题提出能力是一种综合性、创新型能力，很多数学活动（如数学建模前期）都会涉及，而给情境让学生编题则属于相对狭隘的问题提出．G4说：“猜想、疑惑也属问题的范畴，就像每个行当有科班也有杂牌一样，表现形式不同而已．给出情境让学生提问比较局限，这种一定要以问号结尾的主体形式融入课堂实在很难．”G2则持不同观点，指出得从problem posing一词出发去理解，提问是指通过一个现实情境，提出一个新的、有效的数学问题．质疑不属于问题提出，否则只是泛泛提出一些观点，或者质疑某个命题，看到的不是数学问题，因为问题总有条件、有目标．研究认为，这里提问内涵的广义、狭义之分没有对错之别，关乎选择的视角．从研究视角出发对概念严谨性、操作可行性的要求势必削弱问题提出覆盖的范围，而从实际现状出发，形式多样化的问题提出更利于营造相对宽松的环境，促进真实问题的产生[20]．

学者们分别从数学学习和综合素养两个方面肯定了提问培养的教育价值．从数学学习的角度，8位学者认为提问是学生必备的数学核心能力之一，提出新问题是解决问题的重要落脚点．G5说：“问题解决就应该包含问题提出，但是长期以来关注解题，对这块淡化严重，好在目前课标中这块内容已经有所体现了．”G2和J2从学科发展角度，肯定了问题对促进数学学科发展，特别是在中国数学发展中不可替代的作用．G2感慨：“希尔伯特的23问，古希腊几何3大难题这些重要的问题才是推动数学发展轨迹的关键点．中国数学的发展不能总是跟在别人后面修修补补．”从综合素养的角度，7位学者评价指出“提问是创新的基础”．Z3说：“学生缺乏创新能力最主要的是不会提出问题，仅仅会做题永远是被动地学习！”可见，虽然课程文本中问题提出内容占比不大，但在数学教育工作者的心中，培养学生问题提出能力是一项迫在眉睫、不可小觑的任务．

3.2.2 发展与评价

社会诉求、教育改革是近些年对学生问题提出能力关注热切的主要原因，其次也受国际前沿教育研究的影响．几乎所有学者对现阶段中国学生、教师问题提出能力持有消极评价，这点不容乐观．研究源自实践，服务于实践，正如G1这样看待问题提出的评价研究：“结果可能会不尽如人意，优秀学生反应还好，但是一些差一点的学生都不知道往哪个方向想．现状调查研究应该帮助我们了解中国学生提问能力到底强在哪里，弱在哪里．”同样，变式教学作为中国传统数学教育特色，本应是促进学生灵活思考问题、独立创造问题的沃土，但访谈中7位学者对此持保留态度．Z1这样评价：“变式教学本身就是有套路的，是牵着学生走，学生也没有受过提问训练．变式的题目也不是都有价值的，要脱离问题本身，类比联想才更重要．”J2也表示：“敢于将完整的，包括错误的思路过程展现给学生才是教师变式过程中难得的，学生缺乏从错误中学习的经验．”可见，就问题提出能力而言，中国还出于认识反省阶段，课程标准作为教育政策指向的诠释性文本，重视、新增问题提出相关内容是个好兆头．

3.2.3 培养与困境

如何落实培养学生问题提出能力，受访专家们给出了各方面丰富建议．G5从宏观视角提出“观念层面评价先行”“教师培训按章取法”“研究领域摸清认识”3条建议．Z1、Z2从课堂实施出发，认为教学生提问需要结合恰当的具体知识，比如解析几何这种类比和联想性强的内容．Z3则强调课堂教学设计的起点要好，教学梯度和宽窄要适中，对问题要有预计．J1就教材编写介绍说：“人教04版教材对问题提出就很重视，第一次在正文中设置了一些观察、思考、探究栏目．看过问题三百个，不会提问也会模．但是教科书与课堂教学不一样，一字一句都需斟酌，目前不可能呈现直接让学生提问的内容话语，因为教科书呈现有一个循序渐进的过程，且讲究艺术，在最初不是告诉学生要提问，而是引导学生如何提问．”

同时，受访学者一致表示当下培养学生问题提出能力阻力大，而归根结底是考核评价机制的原因．G2认为学生接受一段时间的提问训练，可能提问能力、解题能力、成绩都会有所提升．但可悲的现实情况是：没有这个胸怀容忍类似的研究，实际教学中有时间和能力尝试教学生提问的教师少之又少．

4 研究结论与启示

中国数学课程文件中问题提出能力培养的发展路径可分为3个阶段：教学方法层面的酝酿萌生期、目标驱动之下的初步探索期、自上而下统筹的稳步发展期．该发展路径显示问题提出已被视为一项基本的学习能力，中国对学生数学问题提出能力培养的要求越来越高，这给未来基础数学教育工作带来了新的挑战与压力．就当下的问题提出培养现状，不少学者认为问题提出的广义内涵可能更有助于学生的数学学习和思维发展，过于拘谨地看待问题提出行为很可能会落入狭隘的“研究怪圈”．所有学者都肯定了问题提出培养的价值，认为善于提问是创新特质的具体表现．面对学生薄弱的问题提出现状，学者们认为需要教师和教师教育工作者合作，在思想和行动上实现“双重突破”．

不难发现，中国学生的数学问题提出培养存在课程要求与现实情况“脱节”的现象．以2001年为界点，课程文件早已实现学生问题提出培养从“行为习惯”向“能力意识”的形态转变．反观当下，学生自我提问的习惯似乎并没有养成，其问题意识、问题提出能力的培养也顿足不前．针对类似现象，美国学者分析认为，尽管将问题提出整合到数学课程中的呼吁很高，但教材编写和实际课堂给予学生的提问经验远远少于解题经验[21]．中国学者在访谈中又将此二次归因于相对单一的评价机制．诚然，一项研究难以解答课程文件如何落实进教材等问题，也无法影响国家层面的评价机制，但聚焦实践，针对研究结论得出的具体问题，从课程安排、课堂教学、教育研究3个方面进行反思，得出以下启示．

（1）保护低龄儿童提问意识，逐步推进提问能力发展．

课程文件在各个学段对学生问题提出能力培养的重视程度不同，会使得学生问题提出能力发展无法顺利完成进阶，导致文件要求与现实情况“脱节”．研究统计显示，中国小学数学课程教育阶段对培养学生数学问题提出能力的重视较为不足[22]，课程文件中对小学生问题提出培养的相关表述较少，实际渗透力略显薄弱．初高中阶段有关学生问题提出培养的表述较多，要求更高．其实，低龄儿童的问题最为本初和重要，是生命个体内部矛盾的真实反映，表达了认知的发生、发展过程[23]．有研究表明：儿童在陌生刺激和多样情景中能够接触延伸环境的机会，从而触发偶然的学习[24]．然而随着年龄增长，儿童渐渐变得不愿甚至不敢提问，批判质疑、交流表达等行为也随之减少，久而久之提问意识磨灭殆尽．就此现状，课程文件应针对问题提出能力在各个学段的培养安排上逐步推进，避免断崖式发展．同时，研究还发现百年来的课程文件对学生问题提出能力的培养很少告诉教师该如何针对具体内容进行教学活动设计和课堂实施．因此，建议未来课程文件中的相关表述能够进一步阐明问题提出的内涵价值，同时结合知识内容在教学实施意见或附录处给出具体的操作指示．

（2）创设多样提问教学情境，运用策略揭示提问过程．

积极落实课程标准中的问题提出培养目标，需要学校、教师解放对课程培养、课堂教学的总体把握．保护学生提问的热情意志，创造多样的提问教育环境，是对创新人才诉求的极大支持．现今，中国数学课程实施中，部分教师出于多种因素，会持有一种“围绕既定任务，依照轨道开展”的执念．其实，学生提问的过程虽然复杂但也是智慧的珍宝，看似滴水不漏的教学过程也许是真正需要打破的盒子．同样，问题提出培养的教学实践涉及诸多方面[25]．首先，关于问题提出情境设计，游戏情境、半结构化情境、涉及现实生活和人际交往的情境是重要资源，能够促进学生自然而然地提出创造性问题[26]，对此中国学者认为情境设计需要以辨别学生层次、课型时段为前提，以预设问题数量种类为保障．其次，关于提问策略，其经典代表是美国学者Brown和Walter提出的“否定假设”法（what-if-not）[27]，中国学者也十分倾心于这一策略．研究访谈中有学者表示，如果教师能够展现自己运用策略提出问题的完整过程，乃至错误的经历，对学生而言是不可多得的提问模仿经验．最后，关于课堂实施，需要教师克服畏惧心理，提升掌控课堂自信心，增强培养学生证伪和逆向思维的意识．因此，问题提出培养需要从教材编写、方法策略、活动设计、课堂实施等多方面入手，打破约束过强的条条框框，才能培养真正意义上的提问者．

（3）深度剖析提问思维本质，推进问题提出评价研究．

问题提出的评价问题是难以攻克的教学障碍，也是数学问题提出的研究要点．“评价先行”是破除重“答”轻“问”僵局的关键．早期的评价方法大多基于经验，依靠对问题的复杂度、难度和新颖度的主观判断来考察学生的问题提出表现[28]．后来基于不同视角，研究者似乎不再执着于问题的优劣，转向对提问行为的认知特征、问题情境来源的探索，因此对学生所提问题的分类标准也开始多样化．再后来，研究者们开始使用一些较为严格的分析手段，通过设计复杂任务或者认知评价工具分析问题提出能力及过程．近年来，研究者们对问题提出的评价研究有了新观点，开始尝试对问题多维分析后给出综合性评价[29]．以上评价方式在剖析提问思维本质上还不够深入，也鲜有涉及中小学教师对学生问题提出能力的评价，这需要未来更多的研究继续探索，做出贡献，才能借助评价更好地推进学生问题提出能力的发展．

5 结语

朱子有言：“读书无疑者需教有疑．”培养学生的问题提出能力、创新精神需要大量人力物力投入，不是一朝一夕、寥寥几人就能实现的．因此，从基础教育改革的大背景出发，关注问题提出这一年轻领域，是对培养新时代下新人才的积极响应，也是对当下数学教育课程部分弊端的些许思量．

[1] 胡作玄．现代数学的巨人——纪念希尔伯特诞生120周年[J]．自然辩证法通讯，1982，5（1）：70．

[2] 爱因斯坦．物理学的进化[M]．周肇威，译．长沙：湖南教育出版社，2007：66．

[3] 夏小刚．国内外数学问题提出教学研究的回顾与反思[J]．数学教育学报，2005，14（3）：17–20．

[4] 全美数学教师理事会．美国学校数学教育的原则和标准[M]．蔡金法，译．北京：人民教育出版社，2014：1–200．

[5] 汪秉彝，吕传汉．创新与中小学数学教育[J]．数学教育学报，2000，9（4）：34–37．

[6] 王萍萍，鲍建生，周超．中小学生数学创造力培养的研究述评——聚焦课堂[J]．数学教育学报，2018，27（6）：22–28．

[7] SINGER F M, ELLERTON N, CAI J. Mathematical problem posing: From research to effective practice [M]. New York: Springer, 2015: 3–34.

[8] 中华人民共和国教育部．全日制义务教育数学课程标准（实验稿）[M]．北京：北京师范大学出版社，2001：1–102．

[9] 中华人民共和国教育部．义务教育数学课程标准（2011年版）[M]．北京：北京师范大学出版社，2012：1–132．

[10] 中华人民共和国教育部．普通高中数学课程标准（2017年版）[M]．北京：人民教育出版社，2018：1–180．

[11] 宋乃庆，胡睿，蔡金法．用问题提出和问题解决测试小学生对平均数的理解[J]．数学教育学报，2020，29（3）：1–8．

[12] 课程教材研究所．20世纪中国中小学课程标准·教学大纲汇编（数学卷）[M]．北京：人民教育出版社，2001：1–685．

[13] 中华人民共和国教育部．普通高中数学课程标准（实验）[M]．北京：人民教育出版社，2003：1–122．

[14] 刘易斯．教育研究方法[M]．程亮，译．上海：华东师范大学出版社，2015：692–716．

[15] 施良方．泰勒的《课程与教学的基本原理》——兼述美国课程理论的兴起与发展[J]．华东师范大学学报（教育科学版），1992（4）：1–24．

[16] 代钦，松宫哲夫．数学教育史——文化视野下的中国数学教育[M]．北京：北京师范大学出版社，2011：319–329．

[17] YUAN X, SRIRAMAN B. An exploratory study of relationships between students’ creativity and mathematical problem-posing abilities [M] // SRIRAMAN B, LEE K H. The elements of creativity and giftedness in mathematics. Rotterdam: Sense Publishers, 2011: 5–28.

[18] 波利亚．怎样解题——数学思维的新方法[M]．涂泓，冯承天，译．上海：上海科技教育出版社，2011：16–17．

[19] 弗赖登塔尔．作为教育任务的数学[M]．陈昌平，唐瑞芬，译．上海：上海教育出版社，1995：3–68．

[20] 祝玉兰，曾小平．中小学数学创设情境与提出问题的策略[J]．数学教育学报，2004，13（4）：93–94．

[21] CAI J. An investigation of U.S. and Chinese students’ mathematical problem posing and problem solving [J]. Mathematics Education Research Journey, 1998, 10 (1): 37–50.

[22] 李欣莲，宋乃庆，陈婷，等．小学数学教师“问题提出”表现研究[J]．数学教育学报，2019，28（2）：1–6．

[23] 袁宗金．儿童提问的本体价值[J]．教育科学研究，2010（2）：18–21．

[24] PRUDENCE H, JESUS R. Programming common stimuli to promote generalized question-asking: A case demonstration in a child with autism [J]. Journal of Positive Behavior Interventions, 2001, 3 (4): 199–210.

[25] 温建红．论数学教学中学生提出问题的意义及培养策略[J]．数学教育学报，2014，23（1）：20–23．

[26] ENGLISH L D. Children’s problem posing within formal and informal contexts [J]. Journal for Research in Mathe- matics Education, 1998, 29 (1): 83–106.

[27] BROWN S I, WALTER M I. The art of problem posing [M]. Mahwah: Lawrence Erlbaum Associates Publishers, 2005: 66–109.

[28] ELLERTON N F. Children’s made up mathematics problems: A new perspective on talented mathematicians [J]. Educational Studies in Mathematics, 1986 (17): 261–271.

[29] 夏小刚，汪秉彝，吕传汉．中小学生提出数学问题提出能力的评价再探[J]．数学教育学报，2008，17（2）：8–11．

The Development Path and Enlightenment of the Mathematical Problem-Posing Ability Training in China

LI Mu-hui1, XU Bin-yan1, 2

(1. College of Teacher Education, East China Normal University, Shanghai 200062, China; 2. Institute of Curriculum and Instruction, East China Normal University, Shanghai 200062, China)

At the moment when China’s basic education is deepening its reform, the cultivation of innovative talents cannot be empty words. Starting from the subject and the basics, it is the key to cultivate students’ problem-posing ability. By analyzing the programmatic documents of mathematics curriculum in primary and secondary schools since the 20th century, it is concluded that the development path of cultivating students’ problem-posing ability in China is divided into three stages: the gestation period of teaching methods from 1902 to 1977, the goal-driven initial exploration period from 1978 to 2000, and the steady development period of top-down overall planning from 2001 to 2018. Combined with the research results, the basic experience and enlightenment of cultivating students’ problem-posing ability are drawn as follows: protecting the awareness of young children’s problem-posing, and gradually promoting the development of problem-posing ability; creating a variety of problem-posing teaching situations, and using strategies to reveal the problem-posing process; deeply analyzing the nature of problem-posing thinking to promote the research on problem-posing evaluation.

mathematics curriculum; problem-posing; ability cultivation; development path

G632.4

A

1004–9894（2022）01–0091–06

李沐慧，徐斌艳．中国数学问题提出能力培养的发展路径与启示[J]．数学教育学报，2022，31（1）：91-96．

2021–10–07

教育部人文社会科学重点研究基地重大项目——中国学生数学素养测评研究（16JJD880023）

李沐慧（1994—），女，江苏南京人，博士生，主要从事数学教学、数学问题提出研究．

[责任编校：陈汉君、陈隽]