知识与核心素养视角下中法图形与几何比较研究——基于法国2018版与中国2011版义务教育课程标准
2022-02-18张玉环吴佳桧
张玉环,吴佳桧
知识与核心素养视角下中法图形与几何比较研究——基于法国2018版与中国2011版义务教育课程标准
张玉环,吴佳桧
(河南大学 数学与统计学院,河南 开封 475004)
自2017年以来,“数学核心素养”成为教育界的核心语词和焦点论域,决定着学生在数学上的全面、可持续发展.“图形与几何”不仅是数学的重要组成部分,也是学生进行认知的核心.以法国2018版和中国2011版义务教育数学课程标准为研究对象,首先对两国图形与几何领域知识内容的呈现形式以及知识广度、深度、难度的设定情况进行对比分析;其次基于内涵界定和知识分布两个层面探析两国图形与几何领域主要涉及的数学核心素养;最后结合中国义务教育数学课程标准实际给出启示:适当调整“测量”模块的比重,加强学生与他人有效的数学交流,贯彻算法与编程辅助几何学习.
数学知识与核心素养;数学课程标准;图形与几何;比较研究
1 研究缘起
进入21世纪,世界各国对提高公民素养积极响应,素养的提高离不开基础教育.面对新世纪对人才培养提出的各方面挑战,各国纷纷对数学课程进行改革,出台了适合本国国情的课程改革政策文件[1].当今世界信息高度共享,为顺应时代潮流、紧跟时代步伐,中国也将迎来新一轮的义务教育课程改革.历次课程改革常以数学课程改革为突破口,认为数学课程内容的选择是首要问题[2],作为中国义务教育数学课程标准设置的4大领域之一,“图形与几何”对训练学生的逻辑思维能力有着其它领域难以取代的作用[3].近年来,国内学者从不同角度进行了课程标准的中外比较,取得了不少有价值的结果,涉及到的类型有课程标准整体架构的比较[4]、课程标准理念与目标的比较[5]、课程内容的比较[6]、基于课程标准的能力要求比较[7].其中课程内容研究是教育理论工作者关注的热门话题[8],主要就课程内容设置,知识内容广度、深度、认知分布,以及学段划分等方面进行探讨,涉及的领域涵盖函数[9]、概率与统计[10]、图形与几何[11–12]、微积分[13]等多方面.在中国知网中以“课程内容+比较研究”为主题词可以检索到180篇期刊论文,其中涉及图形与几何领域的仅有10篇,可见目前国内对图形与几何领域的比较研究还有待进一步加强.不少学者基于课程标准的能力要求进行了中外对比,就数学能力的发展历史、现状以及内涵界定差异等方面进行探讨,既包括多个能力的整体分析[14],又涵盖单个能力的细致对比[15].特别地,严虹[16]在对5国初中数学课程标准能力要求进行对比时,试图从内容标准与数学能力深度融合的视角探析各国特色,结论是融合效果并不明显且富有主观色彩,但在内容和方法上为进一步探究内容标准与数学能力的融合提供了宝贵的经验.
目前,国内对于课程标准的比较研究多是从内容标准或核心素养的单方面视角进行剖析,较少综合两个角度进行研究,特别是基于知识分布探析核心素养的特性与内容体现的文献更为罕见.此外,还未有学者对法国2018版课程标准进行比较研究.法国是一个非常重视数学文化及传统的国家,一直以来也处于数学强国的地位,从古至今数学家不断涌现,如费马、柯西等学者均在数学领域闪耀着光辉,为数学发展开辟了新道路,研究法国数学基础教育颇有意义.为此,基于数学知识与核心素养双重视角对比中法义务教育数学课程标准图形与几何领域,注重对该主题主要涉及的数学核心素养做内涵界定与知识分布两方面的对比,以期对中国义务教育课程标准修订工作提供一定的启示与参考[17].
2 研究设计
2.1 研究对象
研究对象源于中国教育部2012年1月出版的《义务教育数学课程标准(2011年版)》(简称“中标”)[18]和法国教育部2018年10月公布的《义务教育数学课程标准(2018版)》(简称“法标”)中“图形与几何”领域.法国义务教育分为3个学段,即第二学段(cycle 2)、第三学段(cycle 3)、第四学段(cycle 4)[19],所包含的年级为一~三年级(CP、CE1、CE2)、四~六年级(CM1、CM2、6e)、七~九年级(5e、4e、3e)[20],为论述方便且能较好与中国对比,将3个学段称为第一学段、第二学段、第三学段.
2.2 研究问题
许多研究表明,课程标准中最主要、最核心的就是内容标准[2],研究者将主要探讨以下问题:中法两国义务教育图形与几何领域中知识内容的呈现形式,以及知识广度、深度、难度有何差异?中法两国义务教育图形与几何领域主要涉及的数学核心素养在内涵界定和知识分布上有何特点?
2.3 研究思路
以中法两国现行的数学课程标准文本为研究对象,主要采用定性和定量相结合的方法.首先,从知识内容层面出发,对其呈现形式以及广度、深度、难度进行对比分析.其次,基于核心素养层面对图形与几何领域主要涉及的数学核心素养做内涵界定与知识分布两方面的对比.数学能力是发展学生数学核心素养的关键所在,而10大核心概念所包含的思想、意识、观念是培养学生数学能力的重要指标,与法标的六大能力均是数学核心素养的重要体现.立足于中标提出的核心概念与法标提出的数学能力,对比中法两国图形与几何领域主要涉及的数学核心素养.知识是素养产生的本源,为素养的发展提供了理论依据,而素养也以知识为载体[21],为此,依据数学核心素养的特点,对其蕴含的最突出的知识内容进行汇总,展开知识分布层面的对比.
3 中法图形与几何领域知识内容比较与分析
3.1 知识内容呈现形式比较
在阐述图形与几何领域知识目标时,中国划分3个学段呈现,其中小学阶段主要涵盖“图形的认识”“测量”“图形的运动”“图形与坐标”4个部分,初中阶段分为“图形的性质”“图形的变化”“图形与坐标”3个部分,显而易见的事实是这些知识内容并没有细化到各个年级,而是作为每个学段的终极目标呈现,虽然凸显出内容结构的整体性,但笼统的内容要求不利于教师清楚地把握课程内容.教师是教学过程中的主力军,如果教师对学生各年级结束时应达到的内容要求还存有疑虑,将会直接影响到教学质量.
反观法国,不仅呈现出各学段的整体目标,而且还详细罗列出学生各年级结束时应掌握的知识内容及其目标要求,这一举措既保障了内容结构的整体性,又促使各年级知识内容之间的联系更加紧密.并结合具体实例将课程标准提到的知识内容逐一进行了剖析,为经验薄弱的教师把握课程内容提供行动指南的同时,也可促使课程标准规定的学生应达到的知识目标得到有效落实.
3.2 知识内容特性比较
知识内容的特性可以从知识广度、知识深度和知识难度来体现,以下逐一论述.
3.2.1 知识广度
知识广度研究的首要任务是对知识点进行统计,知识点有大有小,按最大知识点统计过于笼统,中间层次知识点没有界定标准,不易把控,为此统计尽可能小的知识点.
(1)知识模块的比较与分析.
①中法知识点数量比较.对中法两国课程标准图形与几何领域的知识点数量进行统计,结果见图1.
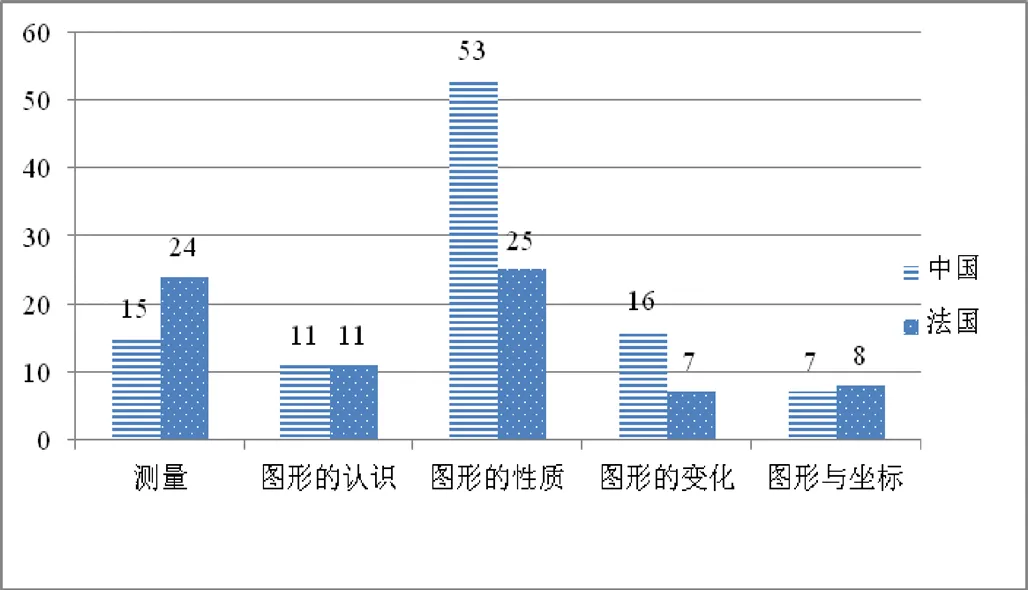
图1 基于模块的中法知识点汇总
如图1所示,“测量”“图形与坐标”模块法国的知识点数量多于中国,而“图形的性质”“图形的变化”模块中国的知识点数量要多于法国.整体上看,中国图形与几何领域知识点个数比法国多27个,即知识广度高于法国.显而易见的是,中法两国占比最高的均是“图形的性质”模块,尤其是中国占据整个内容的52%左右,包含53个知识点,处于该领域的核心地位.
②中法知识异同点比较.对中法两国课程标准图形与几何领域的知识异同点进行统计,结果见图2.
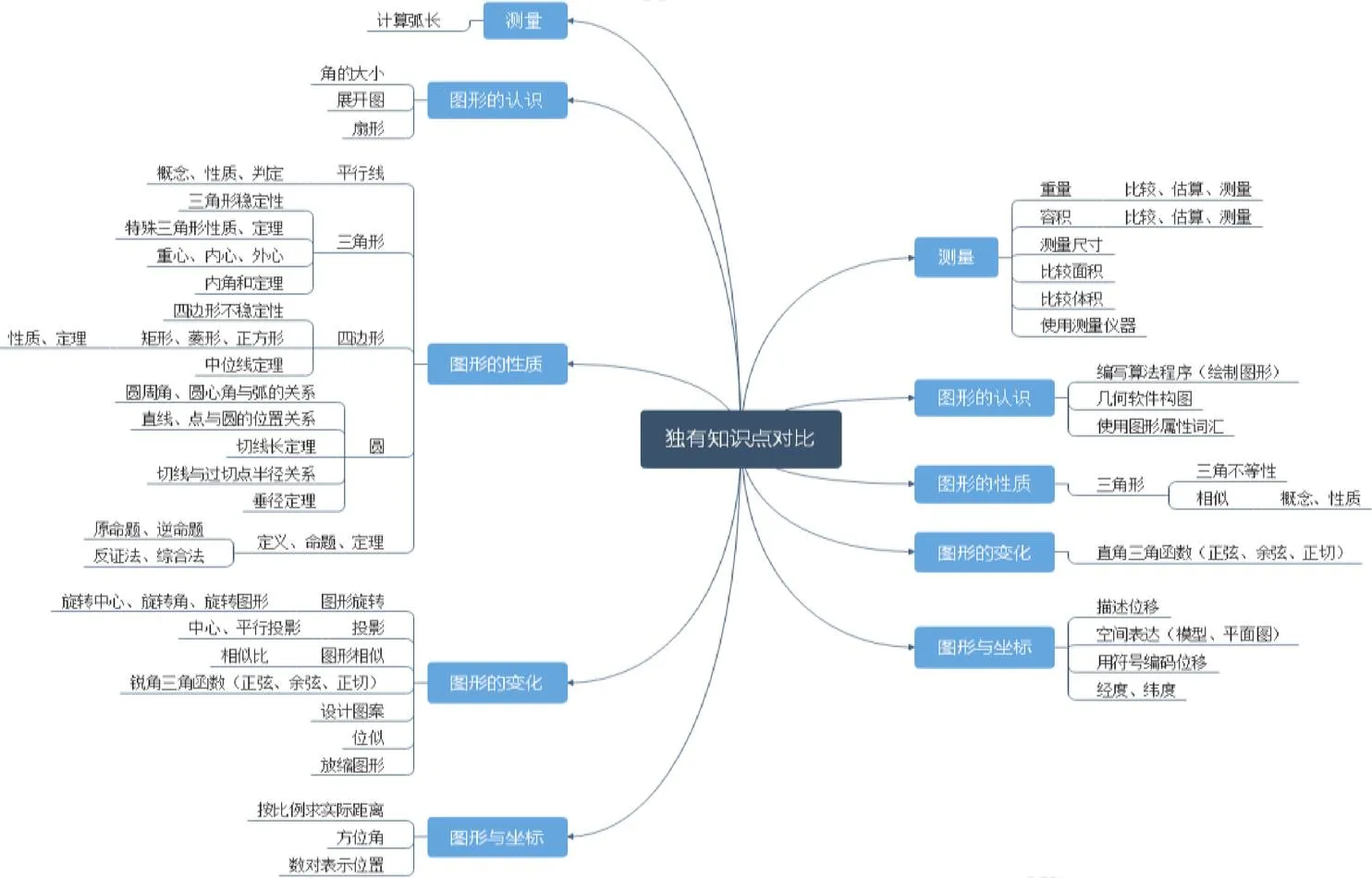
图2 中法两国独有知识点汇总
注:图中左侧为中国,右侧为法国.
如图2所示,“图形的性质”模块中国知识点分布较广,关于三角形、四边形、圆的相关性质、定理均有较全面的体现,而法国只是涵盖个别性质、定理.“图形的变化”模块中国在图形变换方面涉及内容较多,关于图形旋转、投影等知识在法国并未体现.在三角函数方面,中国要求在了解锐角三角函数的基础上掌握特殊三角函数值,而法国仅需了解直角三角函数.“测量”模块法国知识点分布较广,要求学生能够使用多种测量仪器,且能就显示内容进行读数,注重培养学生操作实践以及运用数学解决生活实际问题的能力.“图形的认识”模块法国渗透了算法与编程知识,显而易见的事实是现代信息技术融入几何教学的知识并未在中国涉及.“图形与坐标”模块,法国要求学生能够对平面图、模型进行空间表达,并掌握球体的经度、纬度,帮助学生增强数学学习的现实感和立体感.
(2)学段层面的比较与分析.
如图3所示,中法两国课程标准在第三学段知识点数量相差最大(中国72个,法国28个),知识点交集较小.中国知识点数量随学段逐渐升高,并在第三学段达到最大值,几乎是前两个学段知识点总和的2倍,呈“重末端”现状.相比较来说,法国在各个学段知识点数量比较均衡.

图3 基于学段的中法知识点汇总
3.2.2 知识深度
知识深度的研究依托课程标准对知识点描述时所用词语,以布卢姆教育目标分类学为基础,并结合中国义务教育对数学课程内容要求层次划分方式,将中法两国义务教育数学课程标准对内容要求描述时所用的蕴含递进关系的行为动词分为4个水平:了解、理解、掌握、活用,规定水平权重分别为1、2、3、4[22],如表1.利用公式

计算,其中d=1, 2, 3, 4依次表示了解、理解、掌握、活用4个深度水平;n表示第d个深度水平的知识点个数,n的总和即为本次统计的知识点总数.

表1 认知层次界定参照
(1)认知水平知识分布整体比较与分析.
统计中法两国课程标准在4个水平上的知识点个数,结果见图4.

图4 中法图形与几何认知水平的知识分布
如图4所示,中法两国课程标准要求学生达到“理解”水平的比例最高,在“掌握”水平要求均是最低的.“理解”和“掌握”水平两国差距不大,而在“了解”和“活用”水平分别相差7.16%和6.30%.中法两国课程标准在“了解”“理解”水平比例均高于“掌握”“活用”水平.总体上看,中法两国课程标准在4个水平上的分布情况差距不大.
(2)知识模块、学段的比较与分析.
如图5所示,中法两国课程标准知识深度基本稳定在认知层次2左右.“图形的认识”模块明显看出法国的知识深度高出中国0.540层次,该模块中国要求学生认识、了解图形即可,而法国要求学生会辨认基本图形的同时,还要求能运用几何软件构建图形.相对于中国用认识、了解等行为动词来描述“图形的认识”模块知识的认知要求,法国更多的为运用、构建层次.“图形的变化”模块法国知识深度高于中国0.610层次,这一模块中国知识点数量约是法国的两倍,但其行为动词绝大多数处于了解水平.如位似这一相同知识点,中国要求了解,而法国则要求认识、运用.

图5 基于模块的中法知识深度对比
如图6所示,中法两国课程标准知识深度均随学段的升高而上升,且法国递增的趋势逐渐变大,中国则逐渐趋于平缓,中法两国课程标准知识深度均在2.300层次上下浮动,法国3个学段的知识深度均高于中国.整体上看,法国的知识深度高出中国0.104层次(法国2.364,中国2.260).

图6 基于学段的中法知识深度对比
3.2.3 知识难度
对图形与几何的知识难度研究,首要任务是构建难度测量模型.参考国内相关的课程难度研究方法[23],再基于文献分析,最后确立了知识广度、知识深度的“二维度”难度线性模型:
=(1,2),
=11+22,0<1、2<1,1+2=1.
其中,1表示知识广度,2表示知识深度,模型系数:1=2=0.5.为了更合理地比较,对1、2进行标准化处理,即:1之值为各国课程标准包含的知识点个数与两国知识点总数之比,2之值为各国课程标准知识深度与两国课标知识深度之比,结果见图7.

图7 基于模块的中法知识难度对比
由图7可知,中国在“图形的变化”“图形的性质”这两个模块知识难度均高于法国.“图形与坐标”模块中法两国课程标准知识难度近乎相等且趋于0.500层次.“图形的性质”模块中国在知识内容的3个维度均高于法国,“图形的性质”可视为思维的体操,对发展学生逻辑思维、推理论证等能力有着不可估量的作用.法国在“测量”模块不仅知识点分布较广,且要求也不再是简单的了解层次,更多的是理解、掌握层次,也就造成了知识难度的差异.
如图8所示,中法两国课程标准在一、三学段知识难度近似相等,第二学段法国高于中国.中国的知识难度先减后增,呈“U”形;而法国先增后减,呈倒“U”形.整体上看,法国的知识难度高于中国,难度值分别为0.521、0.480.

图8 基于学段的中法知识难度对比
4 中法图形与几何领域数学核心素养比较与分析
数学核心素养的研究起步较早,却始终没有统一的界定.后来学界参照核心素养这个上位词的概念,给出明确界定,即学生应具备适应终身发展和社会发展需要的必备品格和关键的数学能力[21].这里的“数学能力”是数学核心素养的关键要素,占据核心地位.中标提出的十大核心概念所涉及的思想、意识、观念是塑造学生数学能力的重要指标,是发展学生数学核心素养的关键,其中图形与几何领域中主要涉及的有5部分,即空间观念、几何直观、模型思想、推理能力、运算能力.同样地,法标在“数学综述”部分提出的六大数学能力也均是学生数学核心素养的表现,其中图形与几何领域主要涉及的有4部分,即表征能力、建模能力、推理能力、计算能力.数学知识位居数学体系的核心,具有明显的数学特征,无论是培养数学能力还是思维品质,它都具有强大的纵向融合、横向联系的组织功能.为此,在剖析中法义务教育图形与几何领域主要涉及的数学核心素养内涵界定的基础上,依据数学核心素养的特点,对其蕴含的最突出的知识内容进行汇总,展开知识分布层面的对比.
4.1 关键素养的比较与分析
4.1.1 内涵界定对比
中标提出的空间观念、几何直观是数学教学中一直强调的数学核心素养,内容上和“图形与几何”领域关系紧密,而法标的表征能力内容上既涉及数与代数,又涵盖图形与几何领域,在此主要就图形与几何领域对两国关键素养进行内涵界定对比,具体对应见图9.

图9 中法关键素养内涵界定对应
如图9所示,几何直观与表征能力在内涵界定上一致性程度较高,二者均需要利用图形将复杂的数学问题变得简明、形象,从而降低问题的解答难度,达到预测结果的目的,本质上均是帮助学生更直观地理解数学,不同的是几何直观致力于运用几何模型去转化问题,而表征能力多是借助工具图(图画、示意图、简图、图表)将问题加以转化.空间观念与表征能力在内涵界定上一致性程度较弱,二者均需要进行实物与图形之间的转化,不同的是空间观念侧重空间想象,而表征能力侧重形式转化.
4.1.2 知识分布对比
按两国关键素养描述对课程标准知识内容进行划分并统计,结果见图10、图11.
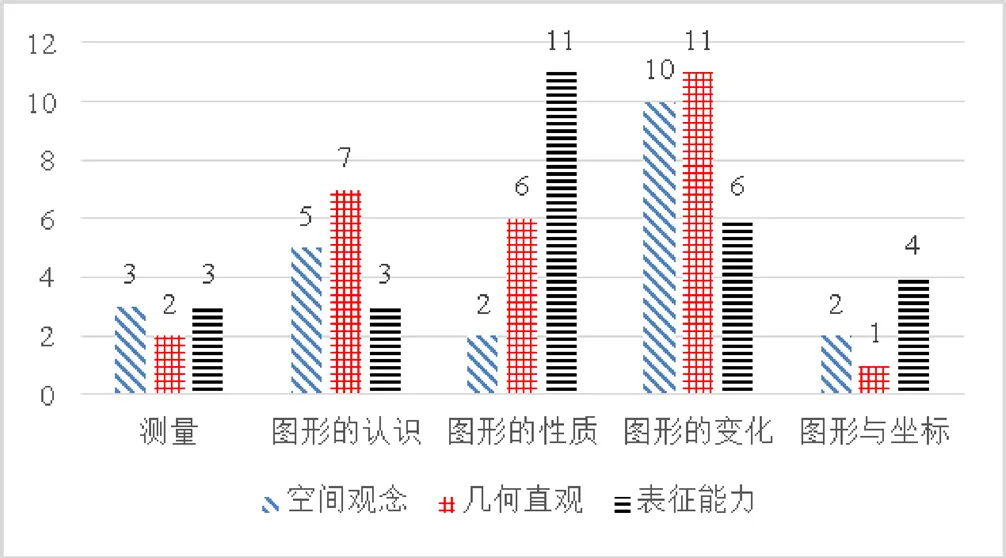
图10 基于模块的关键素养知识点汇总
如图10所示,不难发现“图形的认识”“图形的变化”模块中国空间观念与几何直观涵盖知识点数量均高于法国.空间观念旨在将三维空间的物体抽象成二维图形,研究的问题主要是位置关系、变化规律,几何直观是利用图形认识问题、启发思路[24],可见二者存在重叠部分,即均需要依托图形进行思考和想象,“图形的认识”是进行想象的前提,“图形的变化”是实现想象的工具.
“图形的性质”模块法国表征能力涵盖知识点数量远高于中国.表征能力实质上就是学生运用数学概念的能力,由学生对数学概念、规律的理解来支撑.另外徐斌艳在数学学科核心素养研究中指出表征能力为:“依托书面符号、图形、操作性模型等形式,表达要处理或学习的数学概念或关系,从而解决问题.”[25]这一观点也为上述发现提供了有力支撑.
如图11所示,中法两国对关键素养的重视程度随学段的升高逐渐凸显,其中空间观念在各学段中涉及到的知识点数量较为均衡,几何直观与表征能力的趋势图相近,且第三学段知识点数量高于前两个学段的总和.关键素养的培养需要较高的认知水平,小学阶段学生多处于具体形象思维阶段,对几何的认识多依赖于现实生活中的实物观察,更多的是保留对图形外观的记忆,建立几何直观、制作几何体以及对空间情境进行表征多需要借助抽象思维才可以实现.

图11 基于学段的关键素养知识点汇总
4.2 相似素养的比较与分析
4.2.1 中国“模型思想”对法国“建模能力”
(1)内涵界定对比.
如图12所示,模型思想与建模能力均期望学生能够体会建模和求解的一般过程,即从问题情境中敏锐地捕捉到数学信息,建立相关式子表示问题中的数量关系,并使用数学求解,将数学结果转译为现实结果并进行验证.不同的是,法国建模能力还要求学生能够基于情境信息进行模型归类.经对比发现中国模型思想偏向实用性,强调建模是应用数学知识的重要途径[26],注重提高学生的问题解决能力,法国建模能力注重培养学生类比推理、同化模型的意识.

图12 模型思想与建模能力内涵界定对应
(2)知识分布对比.
按模型思想与建模能力内涵描述对两国课程标准知识内容进行划分并统计,结果见表2.
由表2可知,中国模型思想在“图形的变化”模块知识点数量最多,为7个.模型思想的本质要求是使学生体会和理解数学与外部世界的联系,联系二者的桥梁就是数学模型,这里的模型多指方程式、函数以及各种图形,而绘制图形、建立函数等知识均体现在“图形的变化”中.法国的建模能力在“图形的认识”模块涵盖知识点最多,为6个.法国建模能力注重培养学生的几何思维,特意将能够运用几何模拟实际情境作为能力目标提出,依托图形分析问题的前提是有一定的图形认知.经对比发现,法国建模能力贯穿了算法与编程知识,实现了信息技术与几何内容的有效整合.

表2 模型思想与建模能力知识划分
注:“√”和“○”分别表示包含和不包含该知识点(下同)
4.2.2 中国“推理能力”对法国“推理能力”
(1)内涵界定对比.
如图13所示,中法两国推理能力期望学生在解决问题的过程中既能凭借直觉感知,调用所学知识和方法探索思路、发现结论,又能依托既定规则证明该结论.不同之处在于:①中国推理能力长期以来侧重于在几何教学的作图、证明、计算中培养,而法国推理能力在内容上呈现出跨学科性,即解决的问题可以涉及物理、经济等;②中国强调个人活动,即学生本人通过观察、实验、猜想、证明等数学活动发展推理能力[15];而法国强调合作交流,即学生在推理的过程中与教师、同学展开合作,解释猜想和结论的合理性以发展推理能力;③相比中国,法国还要求学生能够反驳一个判断,注重培养学生的辩证思维.
(2)知识分布对比.
按各国推理能力内涵描述对两国课程标准知识内容进行划分并统计,结果见表3.中法两国推理能力在“图形的性质”模块涵盖知识点最多,分别为15个和8个.
经对比发现,与圆有关的性质定理法国涉及较少,中国特意将其作为“图形的性质”模块中的核心要素进行详细阐述,并要求学生能够进行探索及证明,也就造成了“图形的性质”模块两国课程标准知识广度、深度上的差距.在“测量”模块,法国推理能力涵盖知识点数量高于中国,强调在估算中发展学生的推理能力,为学生提供了自主探索、合作交流的空间.
4.2.3 中国“运算能力”对法国“计算能力”
(1)内涵界定对比.
如图14所示,运算能力与计算能力均期望学生不仅能够依据法则和运算律进行简单的数值计算,代数式、方程的变形,以及逻辑演算(必要时可以借助计算器),并且能够对计算结果进行验证.不同的是中国运算能力要求学生寻求到的最佳解决路径可以体现其思维方式,注重算理,而法国计算能力强调数学技巧及工具的使用,注重算法.
(2)知识分布对比.
按运算能力与计算能力内涵描述对两国课程标准知识内容进行划分并统计,结果见表4.
中国运算能力与法国计算能力均在“测量”模块涵盖知识点最多,分别为6个和8个.经对比发现:法国计算能力所涉知识点多是数值、代数式的计算,且与生活实际联系更为紧密,如“重量”“容积”“尺寸”计算,均是现代社会公民必备的生活技能;中国运算能力所涉及的知识多是基于图形,侧重逻辑演算,这是因为中国运算能力是一个综合性的能力,与推理能力、建模能力相互渗透、相互支撑.
5 研究结论
5.1 知识内容异同
(1)知识内容呈现.
对中法两国义务教育数学课程标准图形与几何领域的知识内容比较可以看出,两国知识内容呈现形式差异较大,中国以学段为依托阐述其内容要求,法国既有学段层面的整体把握,又涵盖年级层面的细致分析.
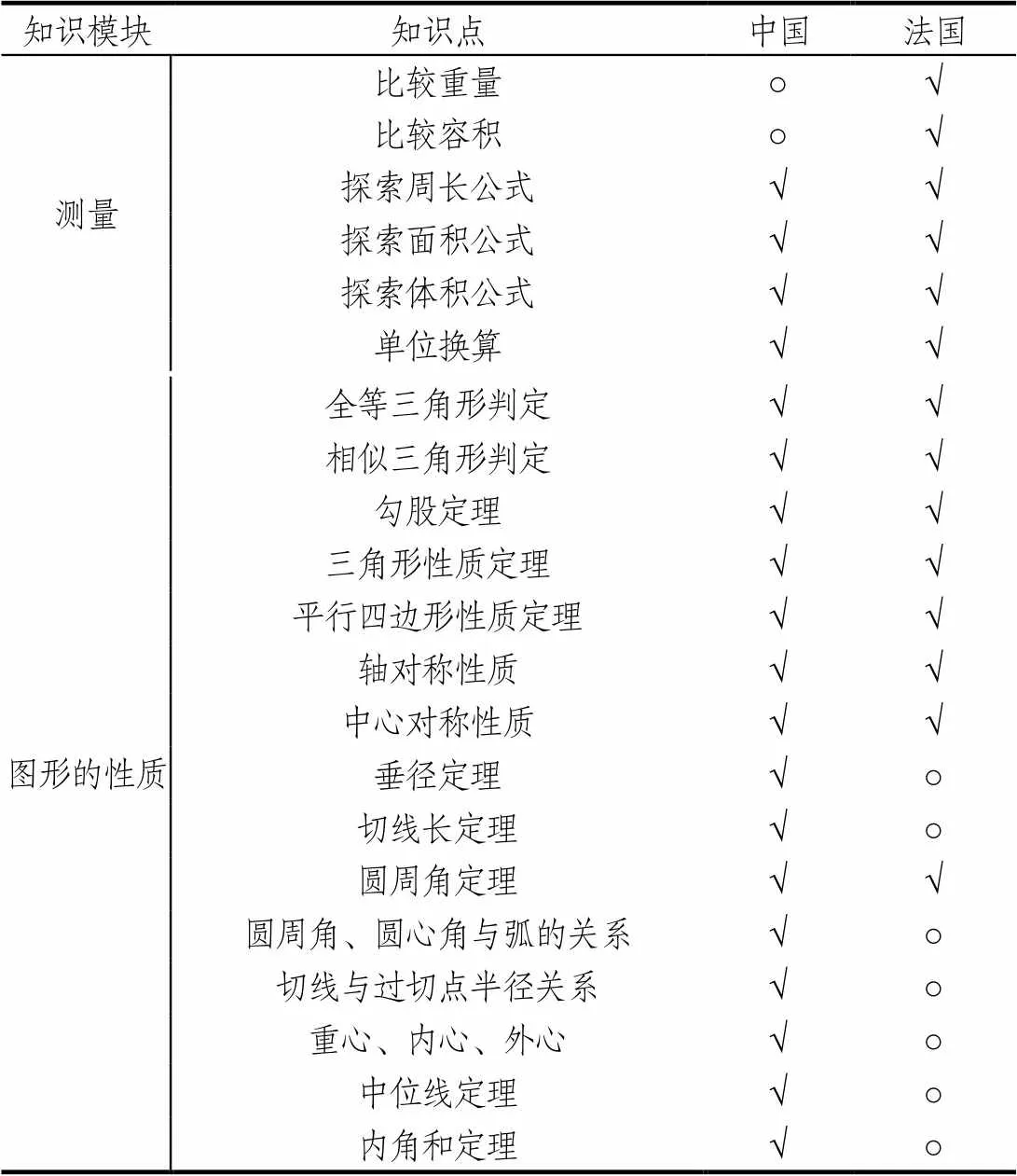
表3 推理能力知识划分
(2)知识广度、深度、难度.
从知识广度方面看,中国明显高于法国,形成这一差异的原因在于“图形的性质”模块,中国所含知识点数量高出法国两倍,该模块位于第三学段,这也是导致中国出现“重末端”现象的关键所在.

表4 运算能力与计算能力知识划分
两国认知水平分布整体差距不大,以至于中法两国知识深度能够基本稳定在认知层次2左右,但显而易见的事实是法国“活用”水平高于中国,可见法国既注重知识的掌握又强调知识的拓展及运用,而中国绝大多数处于“了解”水平,相比法国更注重知识掌握,也就形成了两国知识深度的差异.
两国知识难度差距较大,悬殊之处位于第二学段,究其原因主要在于法国为实现小学、初中两阶段知识内容有阶段性但又无明显界限的衔接,将“图形的性质”模块的部分知识归入第二学段进行学习,该模块的认知水平“理解”“掌握”层次居多,而在中国该模块专属于第三学段.

图14 运算能力与计算能力内涵界定对应
5.2 数学核心素养异同
(1)关键素养.
对中法两国的关键素养对比可以看出,中国的空间观念与几何直观侧重培养学生对几何图形的感知和运用能力,在“图形的变化”模块涵盖知识点最多;而法国的表征能力侧重培养学生运用图形语言转译数学思维的能力,这里的图形可以是几何模型,也可以是图画、示意图、图表等,在“图形的性质”模块涵盖知识点最多.特别地,几何直观与表征能力在内涵界定以及知识分布上一致性程度较高,空间观念与表征能力一致性程度相对较弱.这是因为表征能力与几何直观均是基于一定背景条件对图形进行整体把握的能力,而空间观念倾向于脱离背景想象图形的形状与关系.
(2)相似素养.
经对比发现,两国相似素养存在一定的差异:内涵界定层面,中国的模型思想注重提高学生的问题解决能力,法国的建模能力注重培养学生类比推理、同化模型的意识;中国的推理能力凸显了数学特性,强调个人活动,法国的推理能力呈现出跨学科性,强调合作交流;中国的运算能力强调算理,法国的计算能力强调算法.
知识分布层面,中国侧重在“图形的变化”模块发展学生的模型思想,法国侧重在“图形的认识”模块发展学生的建模能力;中法两国均侧重在“图形的性质”模块发展学生的推理能力,在“测量”模块发展学生的运算(计算)能力.
6 启示
以上对中法两国课程标准“图形与几何”领域的比较,发现了一些差异,存在差异是正常的,不必判定孰优孰劣,他山之石,可以攻玉.通过比较,也进一步了解到中国图形与几何方面的基本情况,得到以下几点启示.
6.1 适当调整“测量”模块的比重
从知识内容与核心素养的对比发现,中法两国义务教育数学课程标准对“测量”模块侧重程度不同.法国较为重视“测量”模块,知识内容的3个维度均高于中国,且涉及知识与学生生活联系更为紧密,如“比较、估算、测量重量”“比较、估算、测量容积”“测量尺寸”等知识,均是现代社会公民必备的生活技能,能够帮助学生认识到数学的价值、亲身体验到数学的应用,有助于调动学生操作实践的积极性,激起学生的参与意识,高效地理解与吸收知识.可见法国义务教育数学课程标准更强调几何课程的现实性与实践性,注重学生参与,突出数学的实用性.这一发现与曹一鸣在初中数学几何分布的国际比较中的结论相对契合,除中国内地外,新加坡、英国、美国等国家都非常注重测量[27].为此,在对义务教育数学课程标准修订过程中应重新审视几何内容,基于中国国情以及未来社会对学生的要求合理调整“测量”模块的比重,保障课程标准的时代性[28–31].
6.2 加强学生与他人有效的数学交流
随着人才需求的改变以及素质教育的推进,数学交流几乎融入到人类交流活动的各个领域,加强学生交流能力的培养已成为当前数学教育改革的一种发展趋势和潮流.法国推理能力特意将“能够听取他人的意见,开展合作”作为目标要求罗列出来,期望学生在推理的过程中既能解释自己的思路与方法,又能以尊重、欣赏的态度倾听他人的观点,就倾听中的疑惑或不同见解进行深入交流,这有利于发展学生的深层次思维,让学生学会多角度、多层面、多途径地探索和分析问题,同时也有助于增强学生的沟通意识、合作精神.特别地,法国义务教育数学课程标准特意将交流能力作为六大能力目标之一提出,倡导学生在进行自我审视的同时学会与他人展开合作,以达到共同进步的愿景,可见法国重视与他人交流,强调合作与共享.中国义务教育数学课程标准虽也提出“清晰地表达自己的想法”“学会与他人合作交流”的观点,但显而易见的事实是中国更加重视自我交流,强调自我审视与反思[23].为此,义务教育数学课程标准修订的过程中可以考虑在不弱化自我交流的基础上加强学生与他人有效的数学交流,帮助学生更深入地理解数学.
6.3 贯彻算法与编程辅助几何学习
21世纪以来,现代信息技术正以前所未有的速度快速发展,且已融入社会的方方面面,尤其对几何教学影响显著,信息技术可凸显几何的直观性,将其融入几何教学对提高学生的学习兴趣,探索除表象以外的知识有着不可忽视的作用[3],如今各国都非常关注信息技术在几何教学中的应用.“算法与编程”是信息技术教学过程中的一个重要模块,法国义务教育数学课程标准在课程内容中将“算法与编程”作为单独的一个领域罗列出来,要求学生在读懂算法指令、理解程序框图的基础上,设计出问题解决的算法,并利用软件执行程序解决问题,在义务教育结束时达到计算机三级的水平[19].特别地,法国将算法与编程知识融入到图形与几何领域,如“图形的认识”模块要求学生编写算法程序绘制图形、运用几何软件构建图形,实现了信息技术与几何内容的有效整合.目前中国义务教育对信息技术与几何内容的整合力度尚且匮乏,为此,义务教育数学课程标准修订的过程中可以考虑在图形与几何内容中融入算法与编程知识,以辅助学生几何学习.
[1] 康玥媛,曹一鸣.中英美小学和初中数学课程标准中内容分布的比较研究[J].课程·教材·教法,2013,33(4):118–122.
[2] 吴立宝,曹一鸣.初中数学课程内容分布的国际比较研究[J].教育学报,2013,9(2):29–36.
[3] 郭民.中英两国义务教育数学课程空间与图形的比较研究及启示[J].外国中小学教育,2012(2):44–47.
[4] 严虹.中美初中数学课程标准比较研究[J].教育探索,2015(10):150–153.
[5] 陈月兰.上海和日本高中数学课程标准中理念与目标比较分析[J].外国中小学教育,2017(11):71–75.
[6] 刘久成.五国小学数学课程内容的比较及启示——基于现行中美澳英日小学数学课程标准[J].外国中小学教育,2016(10):58–64.
[7] 斯海霞,朱雁.中小学数学核心能力的国际比较研究[J].比较教育研究,2013,35(11):105–110.
[8] 赵京波,曹一鸣.中外数学教育比较研究述评——基于CSSCI来源期刊(含扩展版)的可视化分析[J].教育理论与实践,2020,40(2):44–48.
[9] 严卿,胡典顺,汪钰雯,等.中美两国课程标准中高中函数内容的比较[J].数学教育学报,2015,24(4):19–24.
[10] 曹一鸣,王万松.高中概率统计内容设置的国际比较——基于15个国家数学课程标准的研究[J].数学教育学报,2016,25(1):1–4.
[11] 李淑文,史宁中.中日两国初中几何课程内容的比较研究[J].全球教育展望,2012,41(1):82–85.
[12] 刘长明,孙连举.中美两国数学课程标准中初中学段“空间与图形”领域的内容标准之比较[J].数学教育学报,2002,11(4):49–52.
[13] 张玉环,王沛.高中微积分课程国际比较研究——基于十个国家和地区的十四个课标研究[J].数学教育学报,2016,25(2):36–43.
[14] 李颖,谢思诗.中德两国高中生数学能力的分析及比较[J].教育探索,2015(12):153–157.
[15] 王薇.数学交流表达能力目标:中美两国的比较及启示[J].外国中小学教育,2016(11):59–64.
[16] 严虹.基于能力要求的初中数学课程国际比较研究[J].教学与管理,2018(30):80–83.
[17] 本刊编辑部.教育部启动义务教育课程修订工作[J].基础教育课程,2019(2):6–7.
[18] 中华人民共和国教育部.义务教育数学课程标准(2011年版)[M].北京:北京师范大学出版社,2012:1.
[19] Ministère de l'Éducation Nationale. CP, CE1, CE2, CM1, CM2, 6e, 5e, 4e, 3e Mathématiques REPÈRES ANNUELS de progression [EB/OL]. (2018–10–18) [2019–05–10]. http://eduscol.education.fr/pid38211/consultation-reperes-attendus. html.
[20] Ministère de l'Éducation Nationale. Programme des enseignements du cycle 2, cycle3, cycle 4 [EB/OL]. (2018–07–26) [2019–05–10]. https://eduscol.education.fr/pid23199/programmes-ressources-et-evaluations.html.
[21] 喻平.数学核心素养评价的一个框架[J].数学教育学报,2017,26(2):19–23.
[22] 陆吉健,曹一鸣.高中数学“方程与不等式”主题广度和深度的国际比较——基于九个国家数学课程标准的研究[J].教育科学研究,2017(6):63–67.
[23] 蒲淑萍,宋乃庆,邝孔秀.21世纪小学数学教材的国际发展趋势研究——基于对10个国家12套小学教材的分析[J].教育研究,2017,38(5):144–151.
[24] 史宁中.人是如何认识和表达空间的[J].小学教学(数学版),2019(3):13–16.
[25] 徐斌艳.数学学科核心素养研究[J].全球教育展望,2013,42(6):67–74.
[26] 黄健,鲁小莉,王鸯雨,等.20世纪以来中国数学课程标准中数学建模内涵的发展[J].数学教育学报,2019,28(3):18–23.
[27] 马迎秋,曹一鸣.初中数学教科书几何内容分布的国际比较研究[J].数学教育学报,2018,27(4):12–17.
[28] 史宁中,吕世虎,李淑文.改革开放四十年来中国中学数学课程发展的历程及特点分析[J].数学教育学报,2021,30(1):1-11.
[29] 沈中宇,刘思璐,邹佳晨.专家型数学教师的研究与展望——李业平教授访谈录[J].数学教育学报,2021,30(2):61-66.
[30] 路江江,王亚妮.高中数学教育中如何培养学生的数学核心素养——王尚志教授访谈录[J].数学教育学报,2021,30(2):67-70.
[31] 黄荣金,曹一鸣.中国数学教师合作学习的理论和实践:一个国际视角的审视[J].数学教育学报,2021,30(3):1-3.
A Comparative Study of Chinese and French Figures and Geometry from the Perspective of Mathematical Knowledge and Core Competencies——Based on the Compulsory Education Curriculum Standards of France (2018 Version) and China (2011 Version)
ZHANG Yu-huan, WU Jia-hui
(School of Mathematics and Statistics, Henan University, Henan Kaifeng 475004, China)
Since 2017, “mathematical core competencies” has become the core term and focus of the education field, which determines the comprehensive and sustainable development of students in mathematics. “Figures and geometry” is not only an important part of mathematics, but also the core of students’ cognition. Taking the compulsory education curriculum standards of France (2018 version) and China (2011 version) as the research objects, firstly, this study compares and analyzes the presentation forms of knowledge content in the fields of figures and geometry in the two countries, as well as the setting of knowledge breadth, depth and difficulty; Secondly, based on the definition of connotation and the distribution of knowledge, the core competencies of mathematics mainly involved in the fields of graphics and geometry in the two countries is analyzed; Finally, based on the mathematics curriculum standards for compulsory education in China, some suggestions are given: appropriately adjust the proportion of the “measurement” module, strengthen the effective mathematical communication between students and others, and implement algorithms and programming to assist geometry learning.
mathematical knowledge and core competencies; mathematics curriculum standards; figures and geometry; comparative study
G632.4
A
1004–9894(2022)01–0070–09
张玉环,吴佳桧.知识与核心素养视角下中法图形与几何比较研究——基于法国2018版与中国2011版义务教育课程标准[J].数学教育学报,2022,31(1):70-78.
2021–10–07
河南省2021年度教师教育课程改革课题研究项目——学科核心素养背景下职前数学教师评价素养现状及提升策略(2021-JSJYYB- 005);江苏省教育科学“十三五”规划2020年度课题——“教育数学”视角下数学学科教学改革研究——以中小学“微积分”为例(D/2020/01/30);河南大学2019年度本科教育教学改革研究与实践项目——数学师范类课程线上线下混合式教学的实践与研究(HDXJJG2019-20)
张玉环(1983—),女,河南商丘人,副教授,博士,硕士生导师,主要从事数学教育、教师教育研究.吴佳桧为本文通讯作者.
[责任编校:陈汉君、陈隽]
