怎样促进学生提出和解决高价值的数学问题——等腰三角形单元教学对比实验研究
2022-02-18吴增生郑燕红吴海燕王泽峰
吴增生,郑燕红,吴海燕,王泽峰
怎样促进学生提出和解决高价值的数学问题——等腰三角形单元教学对比实验研究
吴增生1,郑燕红2,吴海燕3,王泽峰4
(1.浙江省台州市仙居县教育教学研究中心,浙江 台州 318000;2.浙江省台州市仙居县安洲中学,浙江 台州 317300;3.浙江省台州市仙居县横溪镇新生中学,浙江 台州 317312;4.浙江省台州市天台县赤城中学,浙江 台州 317200)
近几十年来,对问题提出教学的研究卓有成效,问题提出与问题解决的认知关系、与数学与学生的学业成就关系、教学策略、教学模式等诸方面理论架构日趋成熟.但是教学实践案例研究不够广泛和深入,特别是用数据说明教学效果的案例很少.研究以初中“等腰三角形”单元内容为例,提出了“用大观念引领,基于单元整体教学设计,整合已有问题提出教学方法,促进学生提出和解决高价值的问题”的教学策略,在典型的城区学校和农村学校分别选择样本进行教学对比实验,收集数据并用SPSS20.0软件进行分析,并进一步进行效应量(ES)分析.结果表明,用这种教学策略能显著提高促进学生提出并解决高质量的数学问题.
等腰三角形;问题提出和解决;教学对比实验
1 研究背景
“提出问题”是科学研究中的一个重要环节,也是数学思考的开端.1989年,全美数学教师理事会(National Council of Teachers of Mathematics,简称NCTM)颁布的《学校数学课程与评价标准》提出“在数学教学中提供让学生提出问题的机会”的主张,这标志着把“问题的提出”正式作为数学教育的问题来研究,引发了问题提出教学法研究的蓬勃发展.研究者从问题提出与问题解决的关系、问题提出与数学学业水平的关系、问题提出的认知策略、问题提出教学模式及实践等方面展开研究,取得了丰富的成果.(1)问题提出与问题解决认知关系的研究.蔡金法等人进一步明确界定了问题提出教学的相关概念及不同表现形式,明确了问题提出与问题解决相融合的认知机制[1].Christou、Mousoulides、Pittalis和Pitta-Pantazi(2005)通过考察职前教师用动态几何软件工具在平行四边形研究中提出和解决问题能力的关系,发现这些职前教师在提出问题与解决问题活动中的认知表现符合蔡金法等人提出的上述理论框架.(2)问题提出与学生学业成就的研究.蔡金法等人研究发现,学生的问题提出活动可以发展学生的学业成就,反之,学生的高学业成就可以促进其提出好的数学问题(Cai和Hwang,2002;Cai等,2013),Silver(1997)研究发现问题提出促进学生的创造性思维能力,Kotsopoulos和Cordy(2009)等人以初中生为例,发现通过问题提出活动可以改进学生对数学知识的理解[1].(3)问题提出的策略和方法研究.Kilpatrick(1987)提出了一些数学问题提出策略:观念的联结、类比、一般化、反驳、换位思维法和观念组合法等,通过运用这些策略,可以帮助学生提出更多的好问题[2];Silver(1994)提出了两种提出问题的策略:一种是根据情境来提出问题,另一种是改编现有问题来提出新问题[3];Moore-Russo和Weiss(2011)基于数学家决定后续研究方向的常用变式思考方式,以几何内容为例,提出在已有问题基础上提出新问题的5种策略[1]:强化/弱化条件,强化/弱化结论,一般化,特殊化,反向思考.(4)问题提出教学的研究.Contreras(2003)提出的PPM(Problem Posed Model)教学模式认为教师可以通过例题来讲授提出问题的一般模式,激发学生提出问题[4];Kontorovich等人在后续研究中(2012)就课堂上学生特定的集体活动情境,提出了解释数学问题提出复杂性的综合性理论框架:任务的组织、学生的知识基础、问题提出的启发式与图式、小组工作的行为与互动模式及个体对适切性的考虑[5].由Ellerton(2013)提出[6]、并经Xie(2017)[7]等进一步完善的主动学习框架(active learning framework),有助于在真实、复杂的数学教学环境中确定问题提出的位置和师生的角色及其变化.此外,经过Hildebrand(1999)[8]、Contreras(2007)[9]、GonzaLes(1998)[10]、Yeap(2009)[11]、Schloemer(1994)[12]等研究者的努力,在问题提出的教学目标和教学方案、师生角色定位、学习任务设计等诸方面取得丰富的成果.English(1997)在小学五年级5个班级中进行问题提出训练实证研究,从五年级的150名学生中选出11位数感能力强而解决新颖问题弱的学生、4位数感能力弱而解决新颖问题强的学生以及12位两者都强的学生(共27人)参与为期一年的提出问题系统训练活动,通过前后访谈测评数据分析,发现进行问题提出训练的学生在“创造新问题,发展新内容和拓展问题结构”3个指标上取得了较好的发展[13].
Cifarelli和Cai(2005)提出的问题提出与问题解决认知循环理论,揭示了数学问题提出和问题解决的关系,在一般意义上为问题提出与问题解决融合教学提供了宏观的认知活动框架.Silver给出了两种提出问题的策略,明确了数学问题提出的基本分类和基本来源,为问题提出教学提供了可参照的方向.Moore-Russo和Weiss(2011)进一步细化了Silver的问题提出策略,提出了更具有操作性的问题提出方法,便于在教学中整合问题提出与解决活动,达成课程目标;Contreras、Kontorovich、Ellerton、Xie等人的教学模式研究,给出了可操作的教学设计和实施的方法,English(1997)的实证研究,为研究促进学生提出和解决问题能力的教学干预研究提供了有益的启发.
在国内,数学问题提出教学研究始于20世纪90年代,2001—2003年快速发展,然后趋于平稳[14].随着课程改革的深入,“四基”“四能”要求出现在2011版义务教育课程标准及2017版普通高中数学课程标准中,又出现了快速发展的势头.吕传汉、汪秉彝(2006)曾构建数学“情境—问题”的教学模式,给出了问题提出和解决的系统教学策略体系,建立了一个帮助教师设计提出问题情境的项目组,基于通常的课程,引领教师开发出了一系列的教学案例,在中国10个省市超过300所学校参与了该项目的培训与研究[15].蔡金法认为,问题提出教学研究中,对于用问题提出评估师生的数学思维,问题提出教学的理论框架,目前已经基本成型,目前缺的是具体的实践来实现这些理念[16].2019年,蔡金法带领浙江萧山的一批小学数学教师,开发了一批教学案例,发表于《小学数学教学》增刊上.此外,《数学教育学报》于2002—2003年集中发表了数学问题提出教学案例研究的论文.
已有研究表明,开展问题提出教学,能有效促进学生解决问题能力和创造性思维能力的发展(Cai和Hwang,2002;Cai等,2013;Silver,1997);而且也有了促进学生提出问题的策略框架(如吕传汉、汪秉彝提出的“情境—问题”策略,Silver提出的两条策略,Moore-Russo和Weiss基于几何内容的问题提出具体方法,English提出的发展学生问题提出和解决能力的训练框架,等等);通过训练,教师和学生也有能力提出问题.但是,研究中也发现了学生提出的问题质量往往不高,往往会提出非数学、不可解和不相关的问题[17].English(1997)提出的训练问题提出和解决能力的策略框架是针对班级中的部分同学进行的,不能直接迁移到通常课程的课堂教学中,在国内已有的实践研究中,至今很少发现基于数据分析的融合问题提出和解决教学实证研究,导致这些教学案例在改进学生学习、发展学生的问题提出和问题解决能力的效果方面说服力不足.
在许多案例中,教师把学生提出问题的数量作为首选目标,导致课堂满堂问(细节性而繁多的变式问题),没有帮助学生从宏观上基于单元提出研究主题,没有把问题提出与问题研究与解决很好地融合起来.如果说,小学阶段可以通过变式提问实现学生对数学结构的多元理解,改进学习,到了初中高中,这种基于细节的繁多提问会干扰学生的学习.
开展问题提出和解决教学,首先要引导学生提出和解决高价值的数学问题.美国很多学者对提出的问题进行了不同的分类,虽然涉及到提出问题的流畅性、延展性、独创性[18],蔡金法给出了“不好”的问题3个现象——“非数学、不可解和不相关”,但是还没有明确判断问题好坏的一般标准.事实上,“不好的问题”反面,即“数学的、可解的、相关的”是“好”的问题的基础,从数学学科本质上看,什么是“好”的问题?陈省身先生说过,一个好的数学家要知道什么叫好的数学,什么是不好或不太好的数学,有的数学是具有开创性的,有发展的,这就是好的数学;有些数学也蛮有意思,但渐渐变成游戏了[19].这说明,“发展性”是数学好问题的核心特征.此外,学生的学习是基于课程内容的,需要达成课程目标的,“与课程内容及目标的契合性”也应该是好问题的主要特征之一(这里实际上把蔡金法提出的“相关性”特征进行了进一步的可操作性的细化描述).因此,研究者将高价值的问题界定为具有“发展性,可解性,与课程内容及目标的契合性”3个特征的数学问题.问题的发展性指的是提出的问题具有创新性和内生性,能生成一系列新问题;问题的可解性指的是提出的问题在学生知识经验范围内是可解的;与课程内容及目标的契合性指的是,提出的问题反映数学的本质,反映相关课程的核心内容,有利于达成当前内容的课程目标.虽然创新性和情境性也是高价值问题的重要特征,但是在平时课堂中是体现在“发展性”中的.尽管依据课程内容进行的提出问题教学中,学生提出的是课本上的问题,但是对学生来说,如果是新颖的,这样的问题也是他的拓展和创新,问题既可以从现实情境中发现和提出,也可以基于数学内在发展的逻辑来提出.
其次,开展问题提出和解决教学,还要有促进学生提出高价值数学问题的切实有效的教学策略和方法.学生提出问题需要经验支撑,是具有领域特殊性的,需要基于具体内容的学习研究进行,从具体研究过程中形成“怎样研究一类对象”的大观念(Big Ides),引领学生有序地提出高价值的数学问题,这与Contreras(2003)提出的“通过例题讲授提出问题的一般方法”观点一脉相承,也与李怀军、张维忠提出的“以学科大概念为中心选择主题内容,创设情境,引导学生提出和解决问题”的观点一致[20].
数学问题提出,本质上是提出对事物的本质属性、普遍联系和一般规律的疑问,通过数学抽象实现数学化,引入研究对象,明确研究内容和研究目标,是对“在一定条件下能得到事物数量关系和空间形式的哪些属性、关系和规律”的问题表述.在提出数学问题的过程中,需要对情境中对象及其关系进行数学结构化抽象和逻辑推理,这需要直观想象、数学抽象、逻辑推理、数学运算、数学建模、数据分析等关键能力的支撑,它是数学学科核心素养的综合体现;同时也是引发这些数学核心素养相关活动的起点.因此,开展提出问题和解决问题活动,对促进学生数学核心素养的发展,有着重要的作用.
研究者以等腰三角形内容为主题,用数学学科大观念整合各种问题提出教学方法进行研究性单元整体教学设计,用下面3个策略引导学生提出并解决高价值的问题系列:(1)用学科大观念引领,创设现实情境和数学情境引导学生通过类比和联想提出主问题;(2)运用“类比,强化/弱化条件,强化/弱化结论,一般化,特殊化,反向思考”等策略引导学生从主问题中逐步分化出子问题系列,把总目标分解为一系列可达成的子目标,最终达成总目标,解决主问题;(3)通过对问题及其提出和解决过程的反思质疑和类比提出新问题,这与元认知相关.通过教学对比实验,基于数据分析,考察这些教学策略能否促进学生提出和解决特殊三角形内容中新的高价值问题.
2 研究设计
2.1 概念界定
2.1.1 “问题提出”
要在具体内容中实施“问题提出”教学,明确“在教育意义上什么是问题提出”是基础性的.在数学教育中,问题的提出指的是师生为了教学和学习目的而提出数学问题的活动,Cai和Hwang(2019)就数学问题提出从教师的角度和学生的角度做了全面的界定[21],将“问题提出”定义为“师生基于特定情境(问题情境)形成(或再形成)和表达问题(或任务)的活动”,并将教师问题提出分解为5种特定的智力活动:(1)教师自己根据给定的情境提出数学问题;(2)教师预测学生根据给定的情境可能提出的问题种类;(3)教师通过改变现有的问题来提出问题;(4)教师为学生设定能够提出问题的数学情境;(5)教师为学生提出可解决的数学问题.
2.1.2 几何图形研究的大观念
研究表明,专家在解决问题时,具备了围绕核心概念和原理的高度结构化的知识体系,而组织这种结构化知识体系的顶层组织结构、思想和观念称之为大观念,这种大观念有力地支撑了专家比新手具有更强大的提出问题和解决问题能力[22].几何大观念指的是:融合空间视觉和用语言符号表达的逻辑推理研究几何图形的属性及其关系,获得对空间本质的理性认识.具体体现为:如何研究一类图形及其关系的基本路径、内容和思想方法,比如如何通过抽象获得研究对象(从分析典型图形的构成要素及其关系入手),概念的定义方式(名义定义、发生式定义、属加种差定义等,它是确定图形的充分必要条件),几何图形的性质指的是什么(确定图形的必要条件——要素及相关要素各自及相互之间的稳定关系),判定是什么(确定图形的充分条件——要素之间的关系),用什么路径和方法(如抽象的思想、推理的思想、变换思想,定性研究与定量研究相结合的思想)研究等[23].几何图形研究的一般观念也体现在问题提出的层次性和系统性上:首先基于整体情境产生顶层目标,提出主问题;再根据研究思路逐步推进分化出指向总目标的子目标体系,从主问题出发提出层次清晰、指向主问题的子问题系列,通过总结、反思和质疑,提出新的、深层次的问题.
2.2 研究假设
在等腰三角形单元教学中,用几何图形研究大观念引领,创设现实情境和数学情境引导学生通过类比联想提出主问题;在图形特例研究的一般思路和图形变换思想引领下,运用“类比、强化/弱化条件、强化/弱化结论、一般化、特殊化、反向思考”等策略引导学生从主问题中逐步分化出子问题系列,并解决主问题;通过对问题及其提出和解决过程的反思质疑和类比提出新的研究问题.通过这样的教学,可以有效促进学生提出和解决高价值的数学问题.
2.3 样本与变量
选择城区和农村有代表性的两所初级中学作为实验学校,城区学校是某县城典型的大型普通初中,生源较好,农村学校是另一个县的大型普通农村初中,学生水平中等.在城区初中选择4个班级(共187人,其中男101人,女86人),两个实验班(95人,男49人,女46人),两个控制班(91人,男52人,女40人);农村初中选择两个班级共130人(男73人,女55人),一个班级为实验班(67人,男40人,女27人),另一个班级为控制班(63人,男33人,女30人),共选取样本317人.前两章(三角形和全等三角形)章测试成绩都没有显著性差异(>0.05).实验班和控制班由同一位教师执教(教龄10年以上的优秀教师),教学实验前对实验教师进行为期1天的培训,实验过程通过互联网进行伴随指导.通过这些措施,控制学生学业成绩基础变量和教师专业水平变量对教学效果的影响.着重分析实施这些教学策略对学生提出和解决高价值数学问题水平的影响.
2.4 教学对比实验
2.4.1 教学的内容
教学内容是人民教育出版社课程标准教科书(2012版)第13章第三单元“等腰三角形”.
2.4.2 控制班教学方案
控制班根据教材的规定进行常规教学.进行基于知识点的讲解式教学,第一课时为等腰三角形的性质,第二课时为等腰三角形的判定,学习知识点,讲解例题,进行配套练习和作业,习题课1课时,共3课时.
2.4.3 实验班教学方案
采用前文提出的教学策略进行单元整体教学.回顾与复习1课时,等腰三角形整体研究1课时,习题课1课时,共3课时.设计数学内在发展的逻辑情境和现实情境,基于三角形研究的路径、内容和方法引导学生类比直角三角形提出“研究等腰三角形”这一主问题.教师再依据几何图形研究的大观念引导学生规划研究路径,根据研究路径分化出子目标,提出子问题系列,逐步解决主问题.然后,反思和总结问题解决的思想与方法,形成经验,对问题提出和解决过程进行整体评价质疑,提出新问题.基于已有问题提出新问题的过程中采用Moore-Russo和Weiss的基于已有问题提出新问题的策略,通过类比、图形的特殊化和一般化、反向思考(从性质定理的逆命题出发提出判定的问题)等方法提出子问题系列,通过这些子问题的解决最终系统地解决主问题:“怎样研究等腰三角形?能得到哪些研究结论?”在解决了这一主问题后,基于研究过程的反思和总结,可以进一步提出等边三角形和等腰直角三角形(通过特殊化)、含有30°角的直角三角形(通过分割和类比)及不等边三角形(通过一般化)等研究问题.这些将作为评估学生提出和解决高价值问题能力问卷调查中的主要任务.等腰三角形的研究思路如图1所示,教学过程中问题提出过程如图2表示.

图1 等腰三角形研究思路
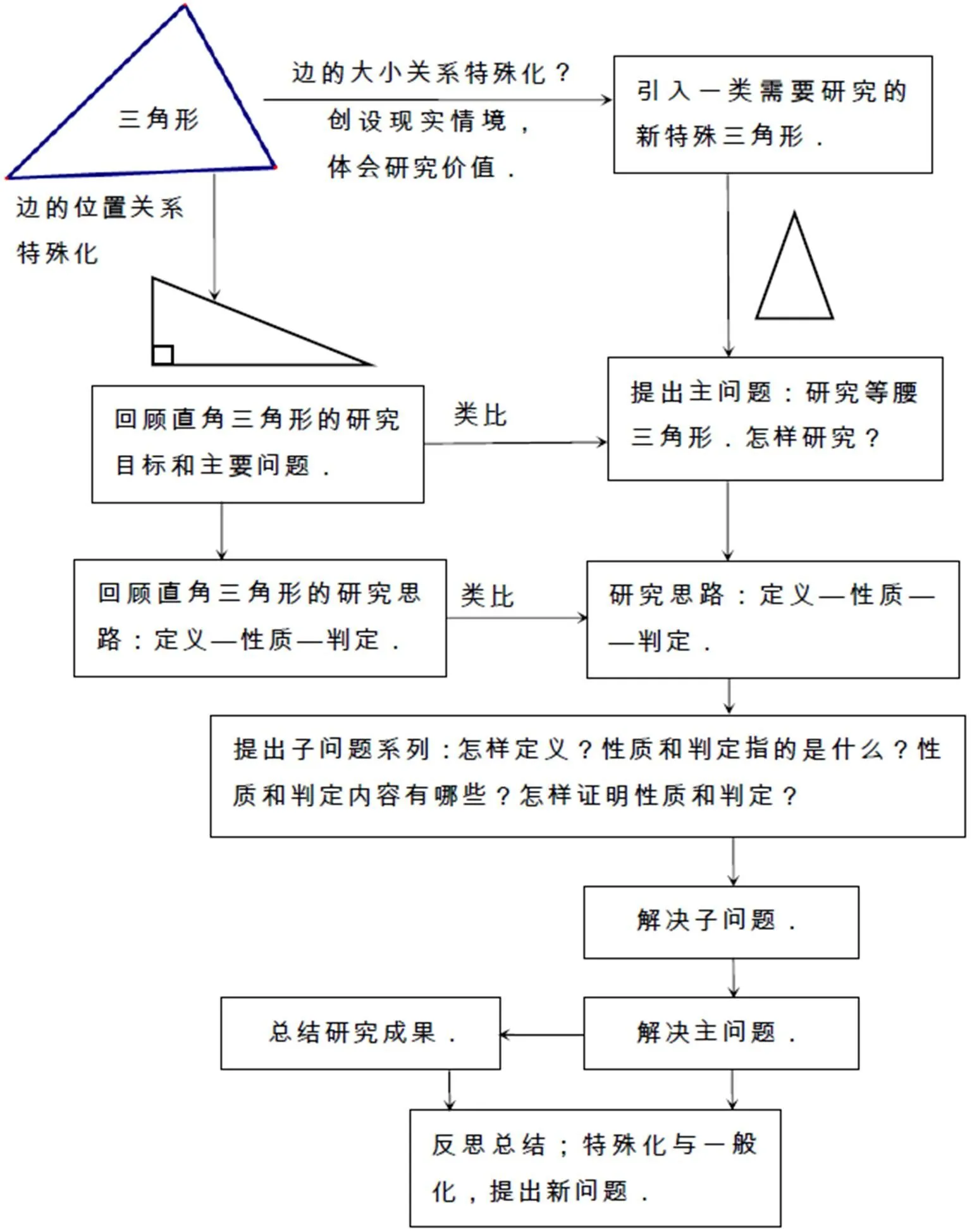
图2 等腰三角形教学中问题提出和解决活动过程
2.4.3 实验班教学过程
*预备教学
总结“三角形”“全等三角形”两章内容的学习经验,比如:如何引入研究对象(从现实情境中引入三角形和全等三角形);从哪些角度定义三角形和全等三角形的(从三角形的边、角基本元素关系角度给出充分必要条件);从哪些角度研究性质(从三角形的边、角这些基本元素和中线、高线和角平分线等相关元素的关系角度探索其不变性);怎样研究三角形全等的判定条件(从三角形的基本元素和相关元素关系出发,寻找能判定三角形全等的充分条件);按照什么路径研究三角形的:给出定义—研究性质—研究关系—研究特例(教科书中安排了对直角三角形两锐角关系的研究,研究的路径是:给出定义—研究性质—研究判定).设计这一预备学习活动的目的是通过复习回顾形成“研究一类几何图形”的数学活动经验,形成几何图形研究的大观念.
*实施正式教学活动
(1)提出主问题.教师创设数学情境和现实情境,运用适当的指导语引导学生引入等腰三角形,提出主问题:研究等腰三角形的空间结构特征.
教师:前面我们在研究三角形的基本性质中,研究了直角三角形这种几何图形,你认为它是由一般的三角形怎样特殊化得到的?类似地,你能提出需要研究的、新的、特殊的三角形吗?
学生:
问题1:研究有一个角为60°的三角形(三角形内角的特殊化);
问题2:研究有一个角为45°的三角形(三角形内角的特殊化);
问题3:研究两边相等的三角形(三角形边的大小关系的特殊化);
……
教师评价启发:在提出的特殊三角形中,两边相等的三角形在现实中出现得比较多(展示生活中等腰三角形形象的图片),因此,首先来研究等腰三角形.
设计意图:创设数学和现实情境,在图形特例研究大观念引领下,通过特殊化和类比引入研究对象.
(2)明确研究目标.教师运用适当的指导语引导学生分析主问题中的研究对象的构成(或决定)要素和相关要素,提出从哪些方面研究主问题.
教师:要研究等腰三角形,你觉得要研究哪些内容?可以类比前面直角三角形和全等三角形来提出要研究的问题.
学生:
问题1 什么是等腰三角形,等腰三角形有哪些性质?怎样判定?
师生活动:教师引导学生回顾等腰三角形的定义,介绍顶角、腰、底边等概念.并进一步提出研究等腰三角形性质和判定问题.
问题2 研究等腰三角形的性质,性质指的是什么?
问题3 研究等腰三角形的判定,判定指的是什么?
教师评价总结:对于一类几何图形,明确定义、研究基本性质和判定,是研究的基本内容.主要从边、角等基本要素以及中线、高线和角平分线等相关要素研究.
设计意图:通过等腰三角形的要素分析,明确研究内容和目标,提出研究的主问题.
(3)规划研究路径.教师通过指导语引导学生规划研究的思路和基本方向.
教师:要用推理的方法研究等腰三角形的性质和判定,类比直角三角形,你能从研究方案的角度提出哪些问题?
学生:
问题1 从哪里出发研究性质和判定?——从定义出发,即从“三角形的两边相等”这个条件出发.
问题2 研究的思路是什么?定义—性质—判定.
教师评价启发:下面,从定义出发,从边、角等基本要素和中线、高线、角平分线等角度研究它们各自的关系,得到三角形的性质.
设计意图:通过类比提出怎样研究的问题,规划研究的思路.
(4)建构等腰三角形性质研究的子问题系统.教师通过指导语引导学生提出性质研究的子问题并加以解决.
教师:从等腰三角形的两边相等这一条件出发,要研究性质,你能提出哪些问题?
学生:
问题1 边有什么性质?
教师评价:这是定义.那么,除此以外还能提出哪些研究问题?
学生:
问题2 角有什么性质?
问题3 中线、高线、内角平分线有什么性质?
教师评价启发:大家能提出这些性质的猜想吗?是怎样发现这些性质的?
学生活动:
用测量、观察和对折实验的方法发现性质:等腰三角形的两底角相等,顶角的平分线、底边上的中线和高线重合,两腰上的中线、高线及两底角的平分线长相等,等等.
教师引导学生进一步通过质疑直观发现的可靠性,提出问题4:为了确定猜想是否正确,需要证明.怎样证明这些猜想?
引导学生进行一步提出派生性问题:
证明几何命题的步骤有哪些?已知条件是什么?结论是什么?
学生活动:独立地证明猜想,写出已知、求证和证明,进行证明过程的交流和质疑,并进一步证明等腰三角形的轴对称性,理解等腰三角形的性质是它的轴对称性在它的构成要素、相关要素上的反映.
设计意图:在图形研究的大观念引领下,理解图形的性质指的是什么,提出性质的研究问题;通过直观观察、想象、归纳的方法提出性质猜想,通过演绎推理证明猜想,得到性质.从而解决性质研究的主问题.
(5)构建等腰三角形判定研究的子问题系统.教师引导学生类比直角三角形研究,依据研究思路,提出等腰三角形判定的子问题,并逐一加以解决.
教师:研究等腰三角形的判定,要解决哪些问题?
学生:
问题1 什么是等腰三角形的判定?满足什么条件的三角形是等腰三角形?
问题2 可以从哪些方面提出等腰三角形的判定?
问题3 可能有哪些判定?
教师启发:能从三角形的构成要素和相关要素出发,找到可以判定三角形两边相等的最少条件吗(从角的关系找,从中线、高线和内角平分线关系找)?
学生活动:通过类比直角三角形的研究,指出从角、中线、高线、角平分线角度通过考察性质定理的逆命题提出判定猜想:有两个角相等的三角形是等腰三角形;一边上的中线、高线和其对角平分线中有两条重合的三角形是等腰三角形(学生可能提出“三线合一”条件,教师引导减少条件得到这个猜想).
教师启发:先从等腰三角形的基本要素边和角的角度研究其判定,在得到等腰三角形判定的猜想后还需要做什么?
学生活动:独立证明提出的判定猜想,画出图形,写出已知、求证及证明过程,进行交流与质疑.
教师启发:现在来研究从三角形的相关元素关系出发研究等腰三角形的判定.
学生活动:学生分组研究,提出猜想,给出证明.
设计意图:在图形研究的大观念引领下,理解图形特例的判定指的是什么,提出判定的研究问题;通过对性质定理的逆向思考,从考察其逆命题中提出判定的猜想.并通过演绎推理证明猜想,解决判定研究的子问题.
(5)引导学生反思总结.教师在等腰三角形的定义、性质、判定等探究环节结束后,引导学生及时地进行反思总结.
定义环节总结:
教师:得到了等腰三角形的定义,能总结一下是怎么得到的吗?
学生:类比直角三角形定义,从边的大小关系的特殊化得到的.
性质研究环节总结:
教师:等腰三角形的性质的条件和结论分别是什么?能总结你的研究过程吗?从哪些方面总结?
学生:等腰三角形性质的条件是“两边相等”,结论是“这两边所对的内角相等,底边上的高线、中线和顶角平分线重合”,这些性质是等腰三角形的轴对称性在等腰三角形的构成要素和相关要素上的反映,是通过观察、归纳提出猜想,再证明的方法研究的.
判定环节总结:
教师:等腰三角形判定的条件和结论分别是什么?能总结你的研究过程吗?从哪些方面总结?你能总结等腰三角形的研究思路、研究内容和研究方法吗?
学生:
等腰三角形判定的条件是“两个角相等”结论是“等角所对的边相等”;条件是“一边上的中线、高线与它的对角的平分线中有两条重合”结论是“其余两边相等”.
等腰三角形的研究思路是:定义—性质—判定.
等腰三角形的研究内容是:性质和判定;从边、角和“三线”角度考虑.
研究方法是:通过直观观察和归纳发现结论,提出猜想,证明猜想;交换性质定理的条件与结论位置,提出判定猜想.一般到特殊的思想,轴对称变换思想、类比的思想.
在等腰三角形研究整体完成后,引导学生总结研究过程及知识结构如图3.

图3 等腰三角形研究活动总结
设计意图:通过分阶段的反思总结,进一步提炼图形特例的研究思路、研究内容、研究方法,发展学生的元认知,为后继学习提供可迁移的问题提出和解决活动经验.
2.5 数据分析方法
2.5.1 设计前后测访谈题目
为了检验这种教学方法能否促进学生在特殊三角形研究领域提出和解决高价值的问题,设计教学前后的两次书面访谈任务作为评价工具.在等腰三角形内容教学前,安排一次前置性访谈I,在等腰三角形内容教学后,安排教学后访谈Ⅱ.两次访谈时间均为60分钟.
访谈I:类比直角三角形,你能通过特殊化提出新的特殊三角形进行研究吗?请你把三角形特殊化后得到尽可能多的新三角形,提出研究问题,选择一类特殊的三角形进行研究,写出研究报告.
访谈Ⅱ:类比直角三角形和等腰三角形,你能发现新的特殊三角形吗?请写出尽可能多的新三角形,画出图形,提出研究问题,选择一类特殊三角形进行研究,写出研究报告.
2.5.2 访谈结果的数字化编码方案
收集学生提出的问题及其解决过程,进行数字化编码(方案事前由研究者设计,编码由非实验教师实施),在数字化编码的基础上,用SPSS20.0分析前后访谈的相关性和均值差异.
提出问题成绩从提出问题的数量和质量两方面进行赋分编码,编码的具体方案为:根据提出符合前文提出的高价值特征的问题数量,每个问题记1分,提出有创新性的主问题每个问题加1分.如在访谈I中提出含45º角的直角三角形研究问题,含有30º的直角三角形等研究问题,含有60º角的直角三角形研究问题,都计1分.如果提出含有50º角的直角三角形,由于在学生认知水平上不可解,则不得分.如果是提出两锐角互余的三角形研究问题,由于实质上是直角三角形研究问题,缺乏发展性,则不得分.如果提出等腰三角形、等边三角形、不等边三角形等问题,因为从新的特殊化角度提出问题,具有创新性和发展性,每个问题记2分.在访谈Ⅱ中,如果提出等边三角形的研究问题得1分,提出等腰直角三角形(或含有45º角的直角三角形)研究问题得2分(因为同时考虑了边的特殊化和角的特殊化),提出含有30º的等腰三角形得1分,如果提出不等边三角形的研究问题得2分,等等.由于提出问题访谈具有开放性,采用按照学生实际提出问题的数量和质量编码方法,不设总分限制.
解决问题的成绩包含定义、性质、判定的数学表达的全面性、准确性,以及推理过程的逻辑性.具体编码方案为:定义0~2分,定义准确2分,基本准确1分,不准确0分;性质0~4分,准确描述性质2分,不够准确1分,不相关0分,证明过程按照严谨性给0~2分;判定0~4分,准确表述2分,不够准确1分,不相关0分,证明过程根据其严谨性给0~2分;提出与教科书不一样的性质和判定加1分,能给出正确证明的,再加3分.满分14分.
2.5.3 数据分析方法
首先用SPSS20.0进行相关检验,分析317位学生的前后测成绩相关性,问题提出的前后测及问题解决的前后测均在0.01水平上显著相关,具有较好的信度.在此基础上,采用SPSS20.0对实验样本和控制样本的问题提出成绩增量和问题解决成绩增量的均值进行独立样本检验分析,并在此基础上进一步计算效应量值(ES Cohen’s),

分析实验样本与控制样本在提出和解决问题成绩增量之间差异,其中的值为0.2以上,0.5以上,0.8以上分别对应着小、中、大的效应.
3 研究结果
用SPSS20.0分析城区学校及农村学校的前测成绩,发现问题提出与问题解决成绩均没有显著性差异(>0.1).再计算问题提出和问题解决的成绩增量(后测成绩—前测成绩),用SPSS20.0进行独立样本检验,城区组结果如表1、表2,农村组结果如表3、表4.

表1 城区学校成绩增量组统计量

表2 城区学校成绩增量独立样本检验

表3 农村学校成绩增量组统计量

表4 农村学校成绩增量独立样本检验
由表1、表2可知,城区学校中,实验样本的在特殊三角形研究领域中问题提出和问题解决成绩提升增量显著地好于控制样本(<0.05).由表3、表4可知,在农村学校,实验样本的在特殊三角形研究领域中问题提出和问题解决成绩提升增量显著地好于控制样本(<0.05).
进一步计算Cohen’s进行效应量()检验,问题提出的增量值和问题解决的增量值Cohen’s计算结果如表5、表6.
问题提出增量中,城区实验样本与控制样本的值为0.56,说明这些教学策略取得中效果,农村实验样本和控制样本值0.81,说明这些教学策略取得大效果.问题解决增量中,城区实验样本与城区控制样本值为0.65,农村实验样本与农村控制样本的值为0.54,说明这些教学策略取得中效果.

表5 问题提出增量Cohen’s d计算

表6 问题解决增量Cohen’s d计算
4 研究结果的讨论
上述数据分析显示,通过研究提出的问题提出和解决教学策略组织教学,可以显著促进学生提出和解决有价值的问题.产生这种效应的原因如下.
第一,根据Cifarelli和Cai(2005)的问题提出和问题解决认知循环发展理论设计问题提出和问题解决相融合的教学宏观结构,让学生完整经历了问题的发现、提出、分析和解决过程,可以帮助学生更深刻地理解问题提出与问题解决的关系,学会从反思和总结已有问题提出和解决过程中总结经验,有利于提出和解决新的有价值的问题.通过给学生创造提出问题和解决问题的机会,让学生在问题提出和解决实践中形成问题意识,形成问题提出和解决的活动经验.
第二,在等腰三角形的教学过程中,让学生完整地经历等腰三角形的性质、判定的研究过程,基于几何图形的直观想象进行概念的形成、性质和判定的语言概括并通过逻辑推理建立知识结构的过程,这符合几何推理能力发展基于视觉空间与语言符号推理相结合的认知原理【Duval(2017)[24],Tall D,等(2012)[25]】,可以比较有效地提高学生的几何推理能力,支撑了等腰三角形研究中几何问题解决活动.
第三,在等腰三角形的研究中,引导学生通过类比提出新的研究问题,发展等腰三角形的知识内容,通过子问题系列细化等腰三角形研究,形成有序分级的问题系统,这符合English(1997)提出的发展学生“创造新问题,发展新内容和拓展问题结构”能力的提出和解决问题能力的训练框架,有利于学生提出和解决问题能力的发展.
第四,对三角形与全等三角形的回顾与复习是用几何图形研究的大观念指导的,这种大观念可以让学生领会组织几何知识及问题提出和解决的“几何直观和语言符号表达的逻辑推理相结合”的顶层观念,引导学生从研究对象的引入和定义、研究思路的规划、研究内容的确定、研究方法的总结等诸方面对已有的三角形及直角三角形研究过程进行整体回顾和整理,获得一类几何图形及其特例研究的大观念,这种通过复习活动获得的几何特殊图形研究大观念,为学生引入新的特殊三角形,提出主问题,提出和解决子问题,最终解决主问题提供了思考的方向标和导航框架.
第五,等腰三角形研究主问题提出过程中,实际上以从一般三角形到直角三角形的特殊化为参照,采用了Kilpatrick(1987)提出的类比策略及Moore-Russo和Weiss (2011)提出的基于已有问题提出新问题的特殊化变式提问方法,类比直角三角形进行,这也为在等腰三角形研究经验基础上通过特殊化引入新的特殊三角形,提出新问题提供了经验支撑.
正是由于上述原因,实验班学生能提出新的一类特殊三角形的研究问题,在几何特殊图形研究的大观念引领下,进行系统的研究,解决新问题,写出研究报告.由于控制班采用了基于知识点的碎片化教学,没有提供提出问题、进行系统研究并最终解决问题等活动机会,也没有几何特殊图形研究大观念的指导,导致学生在面对“没有具体题目”情境时,束手无策,不知道朝着什么方向思考.
5 研究的意义和局限
5.1 研究的意义
首先,研究根据问题提出教学的相关理论,通过教学实践再次验证了Cifarelli和Cai的问题提出和解决交替融合策略的可行性和有效性及Kilpatrick、Silver、Moore-Russo和Weiss、English等人提出的问题提出教学策略的有效性.
其次,研究提出了用几何图形研究的大观念作为学生提出和解决问题的方向标和导航框架,基于单元内容进行教学整体设计,综合运用各种促进学生提出问题的策略和方法,为学生提出和解决高价值的问题提供了方法论上的支撑,能有效促进学生在反思总结的基础上通过类比和特殊化进一步提出新的特殊三角形的研究问题,并能进行系统研究.这是研究的创新点,也可以作为问题提出和解决的新策略应用在今后在课堂中,引导学生提出高价值的问题并加以系统研究与解决.
研究提出的“高价值数学问题”的特征是“发展性、可解性、与数学内容及其学习目标的契合性”,这一观点可以为判断教师和学生提出问题的价值提供一种参照.
最后,研究为等腰三角形内容的问题提出教学提供了一个典型的教学案例,而且这一案例的教学效果具有实证数据的证据支撑.
5.2 局限和展望
虽然研究者考虑到了中国的城乡学校二元差异,分别从城区和农村选择了有代表性的初中学校,对317名学生,6个班级(城区4个班级,农村2个班级)进行教学对比实验,但研究过程并没不包括农村偏远学校,今后需要进一步研究偏远地区学校是否适合这种问题提出教学;其次,总体上学生提出问题的水平还不够高,可能需要长期坚持这种教学方法才能产生更好的总体效果;第三,大观念对数学问题的提出起到了很好的导航作用,但这种专家具有的一般观念是分领域的,今后需要根据不同的内容进行分别研究并进行教学实践验证;第四,研究通过综合应用问题提出的相关理论和几何图形研究的大观念进行问题提出教学研究,影响教学效果的因素可能既有给学生提供问题提出和解决机会的作用,同时还有数学大观念的引领作用,今后需要深入研究这些要素各起到什么作用.
6 研究结论
研究表明,以等腰三角形单元内容为主题,用“怎样研究一类几何图形”的大观念为引领,采用单元整体教学,综合应用Cifarelli和Cai的问题提出和解决交替融合策略,Kilpatrick、Silver、Moore-Russo和Weiss、English等人提出的提出问题教学策略,能显著提高学生提出和解决高价值的数学问题的能力.这些教学策略在等腰三角形内容中可以进一步具体化为:用几何图形特例研究大观念引领,创设现实情境和数学情境引导学生通过类比联想提出主问题;在图形特例研究整体思路和图形变换思想引领下,运用“类比、强化/弱化条件、强化/弱化结论、一般化、特殊化、反向思考”等策略引导学生从主问题中逐步分化出子问题系列,分步解决子问题,最终解决主问题;通过对问题解决过程的反思质疑和类比提出新的研究问题.
研究不仅为这些已有的教学策略的有效性提供了有确定证据的教学实践案例阐释,而且,首次提出了“用数学大观念整合各种问题提出教学方法进行研究性单元整体教学”教学设计思想,给出了3个具体的教学策略,并通过教学对比实验检验其有效性.这为问题提出教学方法应用于课堂教学实践,提供了一条可行的新技术路线.
[1] CAI J, HWANG S, JIANG C, et al. Problem-posing research in mathematics education: Some answered and unanswered questions [M]. New York: Springer, 2015: 3–34.
[2] KILPATRICK J. Problem formulating: Where do good problems come from [M] // SCHOENFELD A H. Cognitive science and mathematics education. Hillsdale: Lawrence Erlbaum Associates, 1987: 123–147.
[3] SILVER E A. On mathematical problem posing [J]. For the Learning of Mathematics, 1994, 14 (1): 19–28.
[4] CONTRERAS J N. A problem-posing approach to specializing, generalizing, and extending problems with interactive geometry software [J]. The Mathematics Teacher, 2003, 96 (4): 270–275.
[5] KONTOROVICH I, KOICHU B, LEIKIN R, et al. An exploratory framework for handling the complexity of mathematical problem posing in small groups [J]. The Journal of Mathematical Behavior, 2012, 31 (1): 149–161.
[6] ELLERTON N F. Engaging pre-service middle-school teacher-education students in mathematical problem posing: development of an active learning framework [J]. Educational Studies in Mathematics, 2013, 83 (1): 87–101.
[7] XIE J, MASINGILA J O. Examining interactions between problem posing and problem solving with prospective primary teachers: A case of using fractions [J]. Educational Studies in Mathematics, 2017, 96 (1): 101–118.
[8] HILDEBRAND C, LUDEMAN C J, MULLIN J. Integrating mathematics with problem solving using the mathematician’s chair [J]. Teaching Children Mathematics, 1999, 5 (7): 434–442.
[9] CONTRERAS J. Unraveling the mystery of the origin of mathematical problems: Using a problem-posing framework with prospective mathematics teachers [J]. The Mathematics Educator, 2007, 17 (2): 15–23.
[10] GONZALES N A. Problem posing: A neglected component in mathematics courses for prospective elementary and middle school teachers [J]. School Science and Mathematics, 1994, 94 (2): 78–84.
[11] HAR Y B. Mathematical problem posing in Singapore primary schools [M] // KAUR B, YEAP B H, KAPUR M. Mathematical problem solving: Yearbook 2009, association of mathematics educators. World Scientific, 2009: 102–116.
[12] SCHLOEMER C G. Integrating problem posing into instruction in advanced algebra: Feasibility and outcomes (Doctoral dissertation) [Z]. Retrieved from ProQuest Dissertations and Theses. (UMI No. 741899141), 1994.
[13] ENGLISH L D. The development of fifth-grade children’s problem-posing abilities [J]. Educational studies in Mathematics, 1997, 34 (3): 183–217.
[14] 尚亚明,何忆捷,熊斌.中国数学问题提出研究的回顾与展望[J].数学教育学报,2019,28(6):81–86.
[15] 吕传汉,汪秉彝.论中小学“数学情境与提出问题”的教学[J].数学教育学报,2006,15(2):74–79.
[16] 蔡金法,姚一玲.数学“问题提出”教学的理论基础和实践研究[J].数学教育学报,2019,28(4):42–46.
[17] CAI J, HWANG S. Generalized and generative thinking in US and Chinese students’ mathematical problem solving and problem posing [J]. The Journal of Mathematical Behavior, 2002, 21 (4): 401–421.
[18] 于文华.美国数学问题提出:是非与评述[J].数学教育学报,2018,27(2):24–28.
[19] 国际数学大师陈省身谈二十一世纪的数学[J].高等数学研究,2001,4(2):2–5.
[20] 李怀军,张维忠.国外“数学问题提出教学法”研究:回顾与前瞻[J].浙江师范大学学报(自然科学版),2020(1):108–114.
[21] CAI J, HWANG S. Learning to teach through mathematical problem posing: Theoretical considerations, methodology, and directions for future research [J]. International Journal of Educational Research, 2020 (102):101–391.
[22] NIEMI D, VALLONE J, VENDLINSKI T. The power of big ideas in mathematics education: Development and pilot testing of POWERSOURCE assessments. CSE Report 697 [Z]. National Center for Research on Evaluation, Standards, and Student Testing (CRESST), 2006.
[23] 章建跃.研究三角形的数学思维方式[J].数学通报,2019,58(4):1–10.
[24] DUVAL R. Understanding the mathematical way of thinking: The registers of semiotic representations [M]. Springer International Publishing, 2017: 1.
[25] TALL D, YEVDOKIMOV O, KOICHU B, et al. Cognitive development of proof [M] // HANNA G, de VILLIERS M. Proof and proving in mathematics education. Springer, Dordrecht, 2012: 13–49.
How to Promote Students to Pose and Solve High-Value Mathematical Problems——A Comparative Experimental Study on Isosceles Triangle Unit Teaching
WU Zeng-sheng1, ZHENGYan-hong2, WU Hai-yan3, WANG Ze-feng4
(1. Education and Teaching Research Center of Xianju County, Zhejiang Taizhou 318000, China;2. Anzhou Middle School, Xianju County, Zhejiang Taizhou 317300, China;3. Xinsheng Middle School, Hengxi Town, Xianju County, Zhejiang Taizhou 317312, China;4. Chicheng Middle School, Tiantai County, Zhejiang Taizhou 317200, China)
In recent decades, the research on the teaching of problem posing has been fruitful. The theoretical framework of the cognitive relationship between problem posing and problem solving, the relationship between mathematics and students’ academic achievement, teaching strategies and teaching models has become increasingly mature. However, the case studies of teaching practice are not extensive and in-depth, especially the cases that use data to illustrate the teaching effect are few. Taking the content of the “Isosceles Triangle” unit of junior high school as an example, the study puts forward the teaching strategy of “leading with big ideas, based on the holistic teaching design of the unit, integrating existing problem posing teaching methods, and promoting students to pose and solve high-value problems”. The samples were selected in typical urban schools and rural schools forthe comparative teaching experiment. The data were collected and analyzed with SPSS20.0 software, and further Effect Size (ES) analysis was conducted. The results show that this teaching strategy can significantly improve students’ ability to pose and solve high-value mathematical problems.
isosceles triangle; problem posing and solving; comparative teachingexperiment
G632.4
A
1004–9894(2022)01–0042–10
吴增生,郑燕红,吴海燕,等.怎样促进学生提出和解决高价值的数学问题——等腰三角形单元教学对比实验研究[J].数学教育学报,2022,31(1):42-51.
2021–10–01
人民教育出版社义务教育课标教材《图形与几何》专题研究(KC2019-057)
吴增生(1962—),男,浙江仙居人,特级教师,正高级教师,浙江师范大学教育硕士导师,教育部第三批国培专家,主要从事中学数学教育研究.
[责任编校:陈汉君、陈隽]
