基于潜在类别分析的小学生早期代数思维水平研究

孙思雨，许添舒，孔企平

基于潜在类别分析的小学生早期代数思维水平研究

孙思雨，许添舒，孔企平

（华东师范大学 教师教育学院，上海 200062）

如何通过算术学习培养小学生的代数思维近些年受到数学教育研究者的关注．研究采用詹姆斯·J·卡普特（James J Kaput）的代数思维理论模型，通过对392名三～五年级小学生的抽象算术、函数思维和数量关系3方面进行调查，利用潜在类别分析（LCA）对学生的答题情况进行分类，研究结果显示：学生的早期代数思维从低到高依次划分为“算术思维、具体的代数思维、一般化的代数思维和符号代数思维”．随着早期代数思维的发展，学生的一般化能力和符号化水平逐渐提高．教师应在算术教学过程中培养学生对“相等”的认识，让学生经历从特殊到一般的过程、鼓励多元表征等活动．

早期代数；代数思维；符号意识；小学生；潜在类别分析

1 问题提出

数学学习是发展儿童抽象、推理和建模等能力的重要载体，是培养学生用数学的眼光看待世界的重要途径[1]．随着课程改革的不断深入，人们对于儿童数学思维的发展也越来越关注．“算术”一直在小学数学课程内容中占有重要的地位，如何挖掘算术学习背后蕴含的数学思想？这是值得思考的话题．其实，算术的学习不仅仅要培养学生熟练的计算技能，更要提供发展学生数学抽象与概括，论证与表征的机会．

国际上小学数学改革反映出这样一个趋势：“小学学习算术，初中再学习代数”的课程设计体系逐渐被改变，代数思维的渗透应该从小学甚至幼儿园开始[2]．随着研究的不断积累，这类研究成为了一个单独的数学教育领域，被称作“早期代数”．在ICME-13专门针对“早期代数”的小组报告会议集中，卡罗琳·基兰（Carolyn Kieran）等人曾对早期代数研究进行总结：“早期代数的研究目前主要关注于6～12岁的儿童在构建数学关系、模式和算术结构时所使用的推理过程，比如注意（noticing）、猜测（conjecturing）、概括（generalizing）、表征（representing）和论证（justifying）．”[2]

虽然中国不提“早期代数”，但是在课程标准和教学实践中都已渗透了早期代数思维培养的思想．例如：《义务教育数学课程标准（2011年版）》在课程基本理念中就明确指出：“学生应当有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等过程．”[3]同时，“符号意识”也包含了“理解并且运用符号表示数、数量关系和变化规律；知道使用符号可以进行运算和推理，得到的结论具有一般性”[5]．除此之外，蔡金法曾对中美的小学数学课程进行比较，发现中国的小学数学课程对于代数思维的处理有三大特点：第一，小学算术中互逆运算同时出现；第二，解应用题时要求学生同时使用代数和算术方法；第三，教材中等式的设计有助于学生对于“等号”的理解[4]．这都表明中国的小学数学课程为学生代数思维的发展提供了基础．

目前，中国对于小学生早期代数思维的研究基本围绕概念介绍[5]、教学设计[6]等内容，对学生代数思维水平发展的研究较少．对学生思维发展的研究有助于教师进一步理解学生、同时可以针对性地进行教学设计．因此，研究提出以下两个研究问题：（1）小学生的早期代数思维可以划分为几个水平？（2）每个水平具有什么样的思维特征？

2 文献综述

如果想要对学生的早期代数思维进行调查，首先需要对早期代数思维的内涵进行界定，其次是对早期代数思维的测量工具进行设计．因此，这里主要对早期代数思维的内涵和早期代数思维测量进行文献综述．

2.1 早期代数思维的内涵

许多人把代数思维仅仅看作利用技巧进行方程的求解，化简和求值，其实代数思维不仅仅是会处理这些代数运算，更重要的是在数学学习过程中具有一般化、建模、数学概括等思维能力．詹姆斯·J·卡普特（James J. Kaput）较早对早期代数研究进行探索，他认为代数主要包含两个核心方面．第一，能够运用越来越正式和传统的符号系统进行概括和表达一般化的结论．第二，能够对规范严格语法（syntax）进行操作．随后，卡普特提出这两个核心由3个方面（strands）体现出来：（1）代数是研究从算术和量化推理（quantitative reasoning）中抽象出来的结构和系统；（2）代数研究函数、关系（relations）和协同变化（joint variation）；（3）代数是用于表征纯数学情境和现实情境的模型语言[7]．

玛丽亚·布兰顿（Maria Blanton）等人就是继承了詹姆斯·J·卡普特的代数理念展开相关早期代数思维的研究．他们的项目LEAP（Learning Through an Early Algebra Progression，简称LEAP）由TERC、威斯康辛麦迪逊大学等机构的研究成员和众多实验学校构成，在早期代数的研究领域具有比较大的影响力．他们将“一般化（generalization）”作为早期代数思维的核心，并且认为早期代数就是指学生在小学阶段对数学结构和关系进行概括（generalizing）、表征（representing）、论证（justifying）和推理（reasoning）的过程[8]．与之类似的，安娜·史蒂芬（Ana Stephen）对小学和初中代数思维的研究进行综述，她认为目前的研究主要围绕在“抽象算术（generalized arithmetic）、函数思维（functional thinking）、数量推理（quantitative reasoning）”3类数学内容，以及“概括（generalizing）、推理（reasoning）、表征（representing）和论证（justifying）”4种思维过程[9]．

综上所述，早期代数思维包含了学生在对数学结构和关系进行概括时经历的一系列思维过程，它是指儿童能够归纳概括出一般化的算式结构、变化规律和数量关系，并且能运用符号来表征和推理论证一般化的结论．它的核心是学生在算术学习过程中培养出来的一般化能力．同时，任何思维的发展都无法脱离知识作为载体，早期代数思维的发展主要有“抽象算术”“函数思维”和“数量推理”3条知识路径．

2.2 早期代数思维的测量

早期代数思维测试主要分为两类，第一类是单独针对抽象算术、函数思维或者数量推理的测试，第二类是对于早期代数思维进行比较全面的测试，同时包含了至少两个内容的测试．由于早期代数的研究还处在初期阶段，大多数研究内容是围绕着它的内涵、课程与教学设计等，因此大规模的测量研究还较少．

与函数思维和数量推理相比，抽象算术的测试卷发展较为成熟，比如帕西佛·马修斯（Percival G Matthews）等人根据前人对儿童认识“等量关系”的认知水平划分，开发出了一套较为全面的测量儿童对于“等式”认识的测试[10]．他们对224名二～六年级的学生进行调查，最后形成了一套包含3种类型、27个题目的测试卷．除此之外，关系性思维的测量也是抽象算术中非常重要的一个方面，并且已经被应用到中国小学生和初中生早期代数思维的测量中来[11]．与抽象算术相比，函数思维和数量推理的测试还未有大规模的测量研究，这些题目比较多地被用于小规模的课堂与教学干预测验当中．

随着早期代数研究的不断发展，近些年逐渐有一些研究者开始开发内容覆盖比较全面的测试卷．在内容结构方面，都是使用卡普特提出的“抽象算术、函数思维和建模”作为理论模型，但是每个维度测试的具体数学知识存在差异．比如玛丽亚·布兰顿等人开发出一套包含11道题目的测试学生早期代数思维的测试卷，用来检验早期代数教学干预前后的学生能力变化，他们将测试内容分为“等式、表达式、不等式，抽象算术，变量，函数思维，比例推理”5个方面[12]．罗尔斯顿·C·尼科尔（Nicole C Ralston）等人通过专家验证、学生测试与深度访谈等4轮修订开发出AAT（Assessment of Algebraic Thinking）．通过对美国华盛顿地区的学生分层抽样得到的397名一～五年级的学生进行测试，得出这是一套信效度良好的早期代数测试卷[13]．该测试卷一共包含25道测试题，涉及建模、抽象算术、函数3块数学内容．除了国外的一些研究，国内也有关于符号意识的测量研究，比如，朱立明的博士论文开发了适合中国义务教育阶段学生的符号意识的测试卷，该测试卷中也包含了许多概括规律、理解变量等一些了内容的测试题[14]．

3 研究方法与过程

研究采用了混合研究的研究范式，其中既包含用数学测试卷对学生的早期代数思维进行调查，还包含对个案进行单独的半结构化访谈．整个研究过程主要包含了以下4个环节（如图1）．

图1 研究流程

3.1 研究对象

由于早期代数思维的测试需要学生具有较高的抽象思维水平，结合课程标准对小学生的能力要求以及学生的现实水平，研究选取三～五年级的学生进行测试．该次测试选择上海地区的两所小学进行数据收集，按照学生平时的数学成绩进行整班分层抽样，尽量保证测试能够涵盖不同能力水平的学生．一共收集到392名学生的测试卷，其中三年级189人，四年级126人，五年级77人．测试卷的完成时间为40分钟，考试过程中由各班的数学教师或者班主任监督考试，以保证试卷的完成质量．

个案是根据对学生的早期代数测试卷结果进行分析之后选择出来，为了使个案具有代表性，以及保证数据的丰富度和有效性，主要依据以下3个原则挑选：（1）要包括不同思维水平的学生都；（2）答题策略较为丰富，或者是某一个策略特别独特；（3）书面体现出较强的表达能力．

3.2 测量工具的编制

测试卷中数学题目的确立经历了两个阶段．首先，如果要保证试卷具有较高的效度需要有清晰的理论框架．结合上文对于早期代数研究的介绍，研究的早期代数思维测量工具主要改编自詹姆斯·J·卡普特早期代数理论框架编制[12]，并结合中国《义务教育数学课程标准（2011年版）》对学生提出的能力要求进行难度调整，具体内容如表1．

表1 早期代数思维测试内容框架

结合表1中的3个主题和不同内容维度，查找相应的数学测试卷，形成试题库．例如，帕西佛·马修斯（Percival G. Matthews）开发的关于“理解相等”的测试卷已经经过了大样本的项目检验，试题比较成熟，并且被许多研究者所使用，因此马修斯的测试题便会被选择进入到“抽象算术”主题中的试题库．同样，“桌子与人数”这个问题情境被许多研究者使用分析学生的函数思维，因此这个问题被归类到“函数思维”试题库当中．根据这样的文献检索建立题库的过程，最后形成了具有16道测试题的早期代数思维测试卷初稿．

第二个阶段是检验专家效度，也就是测试卷的内容效度．研究一共向6位专家放发了“早期代数思维测试专家问卷”，6位专家包括两位小学数学教育专家、两位数学教育博士研究生及两位教龄超过10年的优秀教师，数据结果计算的内容效度指标（）为0.92，这表明测试卷题目的设计具有较高的专家效度．最终根据专家的意见对试卷的题目进行调整，形成了一套具有12道测试题的早期代数测试卷．

3.3 数据编码与分析

3.3.1 数据编码

为了更好地反映出学生的早期代数思维，研究中的测试题均采用双重编码．学生所有的答题情况都会按照“是否正确”和“答题策略使用”两个方面进行编码．回答正确编码为1，错误编码为0．除此之外，根据每个题目具体答题策略情况，会按照1～4进行等级编码．下面主要对学生策略的等级编码进行介绍．

第1～6题是测量学生的“抽象算术”．抽象算术与一般算术的差异体现在，一般的算术题主要要求学生根据具体的数值正确地计算出结果，是一种程序性思维．而抽象算术反映出一种“结构化思维”，或者是称作“关系性思维”，这是指学生不仅仅关注到具体的数值，而是能够发现算式隐含的数学结构[15]．比如，第1题（如图2），处在计算性思维的儿童只能够通过计算67+86=153，68+85=153从而得到相等．但是具有“关系性思维”的儿童可以通过“68比67多1，85比86少1”从而得到等式相等．因此，这道题目一共分为了4个等级：如果完全空白或者（1）选择“错误”得0分；如果（1）选择“正确”，但是理由空白或错误得1分；如果（1）正确，但是理由是计算67+86=153，68+85=153得2分；如果通过关系性思维判断出等式相等则得3分．同理，第2～6题都是按照学生不同层次的思维水平进行编码．

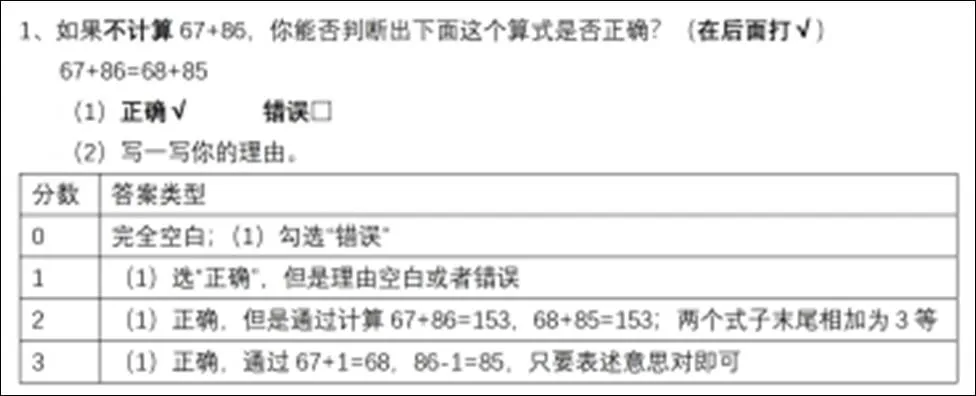
图2 早期代数思维测试卷第1题

第7题、第11题和第12题是考察学生的函数思维．函数思维主要是要求在存在规律的问题中找到自变量与因变量之间的对应关系．以第7题（图3）为例，如果学生可以正确画出第4个图形，表明他可以找到规律．当学生可以找到第20个图形时，表明学生可以找到图形位置与小方块个数之间的关系．因此，这道题目也是分为了4个水平：完全空白的学生得0分；只完成（1）的学生得1分；正确完成（1），并且在第二问的算式中体现出找到了“后面比前面一个多3”的递归规律，但是答案错误的得2分，比如有些学生的算式是“5+3×19=65”；最后一类学生是全部回答正确，比如：5+(20-1)×3=62，或者3×20+2=62会得到3分．

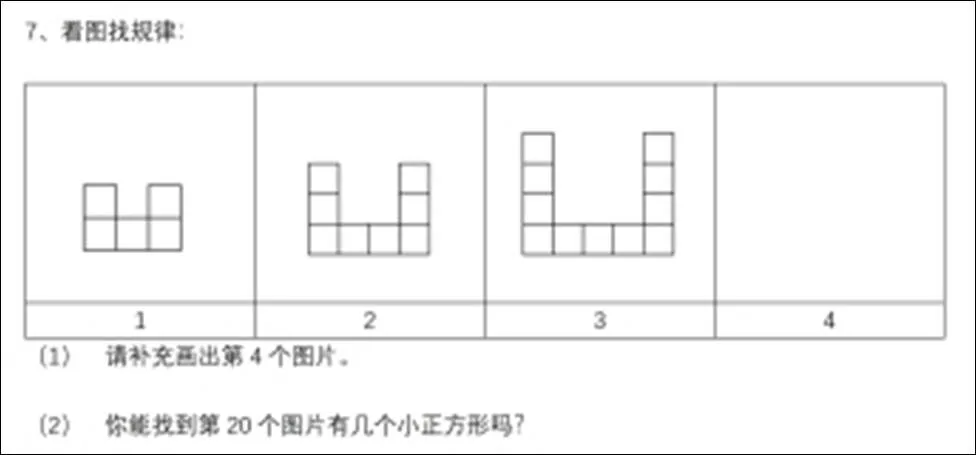
图3 早期代数测试卷第7题

第8～10题是测量学生的数量推理能力（如图4），要求学生能够在没有具体数值的情境中表达不同数量之间的关系．考虑三～四年级学生很难用字母表示关系，这3道题目采用了选择题的方式，并采用二分的计分方式，错误得0分，正确得1分．

图4 早期代数测试卷第8题

由于测试题的编码采取了等级评分，因此需要对评分标准进行评分者一致性的检验．研究随机选择样本中10%的数据，两位评分者根据同一张评分标准进行打分（排除掉第8～10题，这3道题为客观题），结果显示两者的相关性在0.924**到1**之间，这表明该评分标准具有较高的信度．

3.3.2 数据分析

在进行正式的分析之前，研究对原始数据进行了转化．由于不同题目学生的等级不同，因此得分不同．第1～6题为抽象算术的题目，得分均为0～3分．第8～10题为数量关系的题目，得分为0或1．最后为函数思维的题目，第7、11题为0～3分，第12题为0～4分．因此，抽象算术总分18分，数量关系总分3分，函数思维总分10分．为了使不同类型题目的平均分具有可比性，对学生的原始分数进行处理，每道题目的原始分均除以该题的最高分，得到该题的最终得分．

研究主要运用了潜在类别分析的（latent class analysis, LCA）方法对数据进行分析．潜在类别分析是一种基于个体为中心的研究方法，近些年已经逐渐运用到心理学和教育学的研究当中[16]．该方法通过对学生的行为或者答题表现分析，获得潜在类别的具体外显特征，从而将个体分为不同的类别，便于研究者进行进一步的分析．这种方法的优点在于可以更好地将学生划分为不同表现群体，从而理解不同学生在数学内容上的表现特征．研究通过潜在类别分析方法，将在相同题目上具有类似表现的学生归为一类．随后，可进一步通过描述统计分析等方法对同类学生的表现进行质性分析，从而了解小学生早期代数思维的不同类别．研究利用Mplus8.0进行探索性潜在类别分析，并进一步利用SPSS23.0对同类学生的答题表现进行描述统计分析．

4 研究结果

4.1 早期代数思维测试卷质量分析

测试卷一共包含12个题目，它们都是用来测量学生的早期代数思维，因此对整张试卷进行内部一致性检验，结果显示Cronbach’s=0.839，大于0.8，表明信度良好．除此之外，还利用经典测量理论对试卷每道题目的难度和区分度进行分析，难度系数是按照该题答对的人数与全体人数的比值，区分度则通过总分表现前27%和后27%的学生在该题上的通过率之差（鉴别度指数）表示（见表2），试卷的平均难度为0.52，区分度为0.55，表明该试卷具有较好的区分性和适中的难度．

表2 早期代数思维测试卷难度和区分度分析

4.2 学生早期代数思维水平划分

潜在类别分析方法一般从初始模型开始，假定所有样本只存在一种类别，即所有学生都属于一类，然后逐步增加模型中的类别数目，直到找到拟合数据最好的模型．模型的适配检验方法主要有Pearson卡方检验和似然比卡方G2（LL）检验，以及信息评价指标、和样本矫正的（sample size-adjusted）．目前对于模型选择并没有达到统一的标准．通常而言，、和这3个统计量越小越好，和是否显著则表明了第类模型是优于-1个模型．则表示分类的准确性，的范围是0～1，越接近1越好，当>0.6时，表明分类的准确性在80%以上，如果<0.6则表明有超过20%的个体存在分类错误[17]．

研究分别抽取了1～6个潜在类别模型，表示将学生分为1～6类，6种模型的拟合参数具体见表2．从表3中可以看到，从上到下依次减少，在3类时最小，逐渐减少．由于模型的选择没有统一的标准，最终选择主要依赖于数据的可解释度．根据表3中的拟合参数可以看出，研究的样本可以在分3类、4类和5类中进行选择．通过对学生分成3至5类后的表现进行分析，发现分成4类后学生答题特点较为清晰，>0.7表明准确性超过80%，和均显著表明分为4类是明显优于分为3类的模型．根据学生的答题表现，依次命名为：算术思维、具体的代数思维、一般化代数思维、符号代数思维．

表3 小学生早期代数思维潜在类别分析模型比较

注：为自由估计的参数数目，*<0.05，**<0.01．

4.3 不同类别学生早期代数思维表现

4.3.1 不同类别学生整体答题表现分析

通过潜在类别分析，这里将学生分为了4类，通过对4类学生的答题表现进行分析，研究将学生的类别分为：算术思维、具体的代数思维、一般化代数思维、符号代数思维．人数分别是105人、136人、114人和37人．图5是4个类别的学生在抽象算术（generalized arithmetic，GA）、函数思维（functional thinking，FT）和数量关系（quantitative reasoning，QR）3个方面的答题平均分．从“算术思维”到“符号代数思维”，学生在3个方面的平均分依次增高．同时，学生抽象算术的发展一般好于函数思维和数量关系．

4.3.2 算术思维学生特征

算术思维学生只能够对具体的数值进行计算，无法对未知量进行运算，同时也无法理解字母表示数，更加无法理解字母表示变量．以第1题为例，他们只能通过计算等式两边的和来验证等式成立，尽管题目中要求“不计算”．图6是对C2-26号学生的答题情况，研究者对她进行了进一步访谈，F表示访谈者，S表示学生．

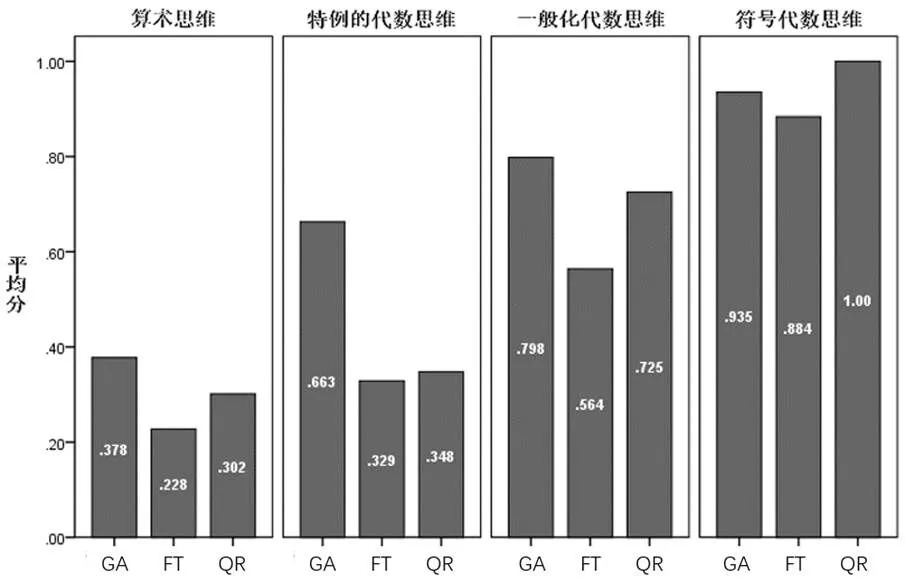
图5 不同类别学生在各个方面的答题平均分

图6 C2-26算术思维答题情况

F：这个第一题你是怎么想的？你觉得有等号的式子一定是相等的吗？

S：（思考了一会）也不一定，像我们平时做一些判断题，也可以是错误的．

F：那你这里写的是什么意思？而且你勾选了“错误”．

S：我当时不会判断，因为它题目说“不计算”．

F：那你知道这个式子是什么意思吗？如果让你计算，你会判断吗？

S：我会的，那很简单，我口算就可以了．

F：那你试试看？

S：67加86是153，右边是68加85是153，所以是相等的．那我写错了……

处在算术思维的学生基本无法完成第8～10题（如图4），因为他们不知道题目里的字母表示什么含义．同样，对于函数思维的题目也基本无法完成，或者只能找到“后面比前面一个多3”的递归规律，但无法求出“较远项”，比如第20个图形有几个小方块．

4.3.3 具体的代数思维学生特征

与“算术思维”的学生相比，“具体的代数思维”学生具有以下3个特点：第一，他们可以通过“关系性思维”来判断等式成立；第二，能够通过“试误法”来求解出等式中的未知量；第三，能够在函数思维的题目中发现“增加1张桌子，就增加3个人”的共变规律，但是只能对具体的项计算，无法概括到一般化．图7是D4-20的一位“具体的代数思维”学生第1题和第3题的解答过程：该学生只能通过尝试不同值（“试误法”）来找到☆的值，还无法运用“逆运算”或者“两边各去掉一颗星”来求得“五角星”的值．但是她的第一题并没有具体计算等式两边的和，而是通过“关系性思维”判断等式相等，这说明她已经具有了初步的代数思维．

图7 D4-20“具体的代数思维”第1题和第3题答题情况

这类学生能够对有限的例子进行推理，但是无法概括到一般化，也无法用字母来表征概括出的规律．例如，图8是D3-6学生在第5题和第6题的答题情况．第5题中可以正确完成前两题，但是当出现时无法进行解答．同样，第6题中可以找出具有相同规律的特例，但是无法用语言或者字母符号表征出一般化的规律．总结来说，这类学生已经具有了初步的代数思维，但是仅能够对具体的例子进行推理，无法概括到一般化，因此称作“具体的代数思维”．

4.3.4 一般化代数思维学生特征

与“具体的代数思维”学生相比，“一般化代数思维学生”表现在：（1）能够运用逆运算或等式的基本性质求解未知数（如图9）；（2）能够对算式结构等概括到一般化，但不能用字母符号准确表达；（3）能够用具体的数值代替题目中抽象的符号进行推理．

处在这个思维的学生虽然可以找到规律，但是由于还没办法运用字母符号进行概括表征，只能通过画图或者表格的方式来呈现规律．如图10是C2-4“一般化代数思维”学生第12题的答题情况，以下是对他的访谈．

F：你这个第20个是怎么想到的？

S：我发现人数每次增加3，然后就依次加3，就得到了62．

F：那如果是第张桌子，你知道是什么意思吗？

S：表示无数张吗？

F：就是告诉你任意一个桌子数，你能知道小朋友的人数吗？

S：如果是太多的话，一直加3，我就不知道该是多少人数了，个人？

F：为什么是个人？

S：因为张桌子说明很多人，无穷多的桌子就是无穷多人．

F：那你觉得和“-1”，谁大？

S：一个数无穷大之后就没有办法比较了．

图8 D3-6“具体的代数思维”第5题和第6题答题情况

图9 D4-36“一般化代数思维”第3题答题情况

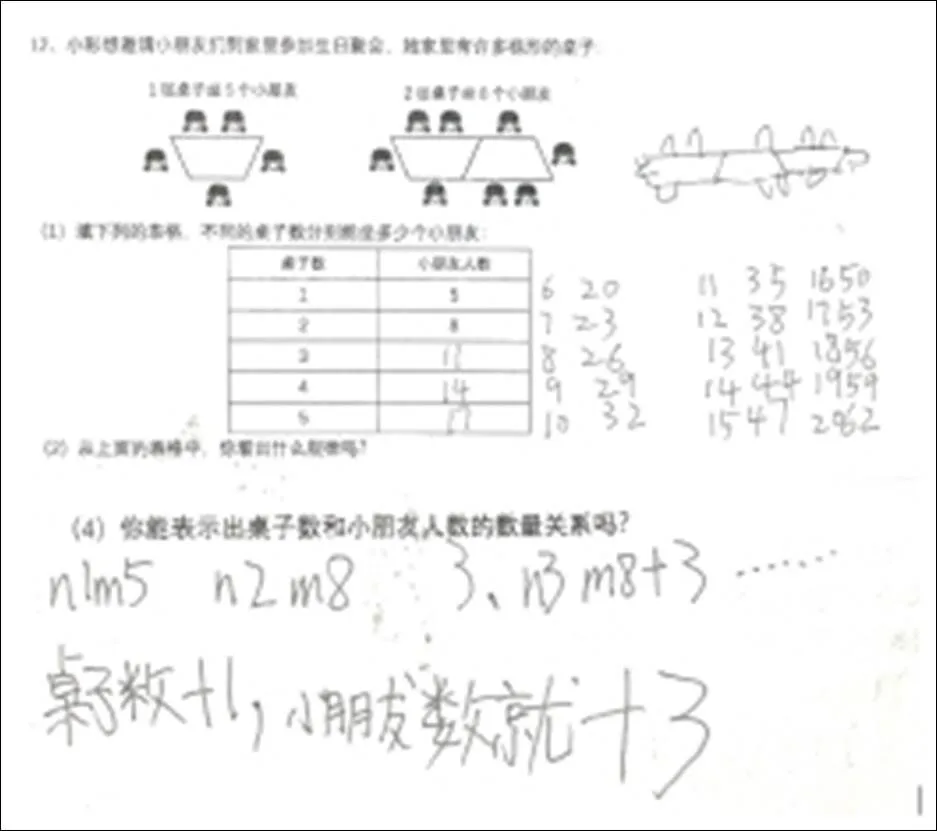
图10 C2-4“一般化代数思维”第12题答题情况

4.3.5 符号代数思维学生特征

虽然广义的符号包含文字、图表等形式，但这里的符号主要指学生已经会用“字母”这种最为简洁的形式化符号进行推理．符号代数思维学生已经可以熟练地运用字母符号进行抽象地推理和概括规律，并且可以理解字母表示变量．图11是D2-19号“符号代数思维”在数量关系和函数思维题目上的答题．

图11 D2-19“符号代数思维”第10题和第11题答题情况

符号代数思维就已经属于较高水平的代数思维，学生能够对字母进行运算，并且用字母进行数量与函数关系的推理．处在这个思维水平的在抽象算术的问题中可以灵活运用“关系性思维”，利用等式的基本性质解决未知数，以及用字母来概括算式结构和规律．对于函数思维的题目也可以找到“远项”的求解（如图12）．

图12 “符号代数思维”第12题答题情况

5 讨论与结论

研究主要是为了了解小学生早期代数思维的不同发展水平，并且分析不同发展水平的学生具有怎样的外在表现特征．针对研究问题，研究利用了潜在类别分析的方法对三～五年级的小学生早期代数思维进行划分，根据学生的答题表现将其分为算术思维、具体的代数思维、一般化的代数思维和符号代数思维4种类型的学生，研究得到以下发现．

第一，随着学生早期代数思维发展，概括化和符号化程度逐渐提高，且概括能力的发展先于符号意识．代数思维发展较好的学生也拥有更高的概括能力，这表现在他们能够发现和归纳出算式结构和图形规律等，但是，学生在概括时所用的符号方式并不严谨，例如，用表格或自然语言等非正式符号来表征所发现的结构和规律．代数思维的特点之一是“能够运用越来越正式和传统的符号系统进行概括和表达一般化的结论”[7]．通过学生的答题表现发现，越是代数思维发展好的学生越能够选择正式的字母符号进行表征．虽然许多早期代数研究者也并不强调学生要用正式的代数符号来进行推理论证[18]，但代数思维的发展与符号意识息息相关，早期代数思维的培养应该注重发展学生的表征能力，鼓励学生用自己的方式来表征，例如，让学生用表格、线段图、画图等方式来表征规律和关系．

第二，函数思维发展晚于数量关系和抽象算术，并且学生在抽象算术方面发展突出．随着代数思维的不断提升，学生能够通过关系性思维、逆运算、等式的基本性质等方法求解等式中的未知量．在目前的小学数学课程里，五年级才开始学习方程和等式的基本性质．实际上，小学生从一年级学习计算时就已经开始发展对于“等式”的理解．因此，小学低年级的算术教学不应仅仅围绕对具体的数字进行操作性的计算，而是要加深学生对于“相等”的理解．“等号”不仅仅是表示计算结果的输出，而是表示两边相等．学生理解“相等”应该是从学习算术之初就开始，贯穿于整个数学学习的过程．与抽象算术相比，学生函数思维的发展较为落后，调查发现，与求解等式中的未知数、对数量关系进行推理相比，理解变量是更为困难的．这与许多之前字母表示数的研究相符[19]．这对字母表示数的学习提供了认知基础，教师可以按照“字母表示未知数”“字母表示一类数”“字母表示数量关系”和“字母表示通项”的顺序进行教学安排．这样的设计会更加符合学生的认知规律，更有利于学生接受字母表示数这种抽象的数学语言．

通过与国外学生早期代数思维发展研究相比[20]，中国学生在“抽象算术”和“数量关系”两个方面表现突出，尤其体现在对于等号的理解、对于数量关系的概括两个方面．但是，这并不意味着中国的学生在“理解相等”或“数量关系”方面不存在困难，由于研究选择的调查样本为三～五年级的学生，而学生对于“等号”的理解等内容在中国一年级的课程中便有涉及，因此今后的研究可以进一步关注低年级儿童的早期代数思维发展．其次，研究对早期代数思维的关注有助于丰富小学算术课程的内涵，从“一般化”和“符号化”的视角理解算术课程可以改善教师在算术教学中“重技能而轻算理”的现象，将算术学习与“符号意识”与“模型思想”的发展联系起来，促进学生抽象与概括能力发展．最后，研究将心理学中的方法运用到学生数学思维的分析当中，丰富了对于儿童数学思维的研究，帮助教师更好地理解学生代数思维的发展路径，从而设计符合学生认知发展的课堂教学．

[1] 史宁中，林玉慈，陶剑，等．关于高中数学教育中的数学核心素养——史宁中教授访谈之七[J]．课程·教材·教法，2017，37（4）：8-14．

[2] KIERAN C, PANG J S, SCHIFTER D, et al. Early algebra: Research into its nature, its learning, its teaching [M]. New York: Springer, 2016: 10.

[3] 中国人民共和国教育部．义务教育数学课程标准（2011年版）[M]．北京：北京师范大学出版社，2012：3-6．

[4] 蔡金法，江春莲，聂必凯．我国小学课程中代数概念的渗透、引入和发展：中美数学教材比较[J]．课程·教材·教法，2013，33（6）：57-61．

[5] 蒲淑萍．国外“早期代数”研究述评[J]．数学教育学报，2014，23（3）：92-97．

[6] 王薇．基于算术教学，渗透代数思维——低年级学生“早期代数思维”培养的实践与思考[J]．数学教学通讯，2018（4）：37-38．

[7] KAPUT J J. What is algebra? What is algebraic reasoning [M] // KAPUT J J, CARRAHER D, BLANTON M, et al. Algebra in the early grades. New York: Taylor & Francis Group, 2008: 5-17.

[8] BLANTON M, BRIZUELA B M, STEPHENS A, et al. Implementing a framework for early algebra [M] // CAROLYN KIERAN. Teaching and learning algebraic thinking with 5-to 12-year-olds. Cham: Springer, 2018: 27-50.

[9] STEPHENS A, ELLIS A, BLANTON M, et al. Algebraic thinking in the elementary and middle grades [M] // CAI J. Compendium for research in mathematics education. Reston: NCTM, 2017: 386-420.

[10] RITTLE-JOHNSON B, MATTHEWS P G, TAYLOR R S, et al. Assessing knowledge of mathematical equivalence: A construct-modeling approach [J]. Journal of Educational Psychology, 2011, 103 (1): 85-104.

[11] 王旭．初一学生关系性思维的表现与特征[D]．上海：华东师范大学，2009：55-56．

[12] BLANTON M, STEPHENS A, KNUTH E, et al. The development of children’s algebraic thinking: The impact of a comprehensive early algebra intervention in third grade [J]. Journal for Research in Mathematics Education, 2015, 46 (1): 39-87.

[13] RALSTON N C, LI M, TAYLOR C. The development and initial validation of an assessment of algebraic thinking for students in the elementary grades [J]. Educational Assessment, 2018, 23 (3): 211-227.

[14] 朱立明．义务教育阶段学生数学符号意识发展水平研究[D]．长春：东北师范大学，2017：40-53．

[15] 刘久成，刘久胜．代数思维及其教学[J]．课程·教材·教法，2015，35（12）：76-81．

[16] 张洁婷，焦璨，张敏强．潜在类别分析技术在心理学研究中的应用[J]．心理科学进展，2010，18（12）：1 991-1 998．

[17] 王孟成，毕向阳．潜变量建模与Mplus应用（进阶篇）[M]．重庆：重庆大学出版社．2018：13-23．

[18] RADFORD L. The progressive development of early embodied algebraic thinking [J]. Mathematics Education Research Journal, 2014, 26 (2): 257-277.

[19] BRIZUEL A, BÁRBARA M, BLANTON M, et al. Children’s use of variables and variable notation to represent their algebraic ideas [J]. Mathematical Thinking and Learning, 2015, 17 (1): 34-63.

[20] CHIMONI M, PITTA-PANTAZI D, CHRISTOU C. Examining early algebraic thinking: Insights from empirical data [J]. Educational Studies in Mathematics, 2018 (5): 1-20.

Research on the Early Algebraic Thinking Level of Elementary School Students Based on Latent Class Analysis

SUN Si-yu, XU Tian-shu, KONG Qi-ping

(The College of Teacher Education, East China Normal University, Shanghai 200062, China)

In recent years, how to cultivate the algebraic thinking of elementary school students through arithmetic learning has attracted the attention of mathematics education researchers. This study adopts the algebraic thinking theoretical framework of James J Kaput, and investigates the generalized arithmetic, functional thinking and quantitative reasoning of 392 elementary school students in grades 3 to 5. The students’ responses were classified by latent class analysis (LCA). The results show that students’ early algebraic thinking can be categorized into “arithmetic thinking, concrete algebraic thinking, generalized algebraic thinking and symbolic algebraic thinking” from low to high. With the development of early algebraic thinking, students’ generalization ability and symbolization level improve gradually. Teachers should cultivate students’ understanding of “equivalence” in the process of arithmetic teaching, allow students to experience the process from special to general, and encourage multiple representations and other activities.

early algebra; algebraic thinking; symbol awareness; elementary school students; latent class analysis

G623.5

A

1004–9894（2022）01–0052–07

孙思雨，许添舒，孔企平．基于潜在类别分析的小学生早期代数思维水平研究[J]．数学教育学报，2022，31（1）：52-58．

2021–10–05

上海高校“立德树人”人文社会科学重点基地“上海基础教育教材建设”项目——数学新编教材与核心素养的一致性研究（14800-412224- 20A07/005）

孙思雨（1992—），女，河南安阳人，博士生，主要从事小学数学课程与教学研究．

[责任编校：张楠、陈汉君]