数学文化融入中学教科书的内容与方法

王 嵘

数学文化融入中学教科书的内容与方法

王 嵘

（人民教育出版社 课程教材研究所，北京 100081）

数学文化在教科书中的融入在一定程度上决定着数学文化课程目标和课堂教学的实现．历经三版教科书编写研究，初步构建了数学文化融入教科书的理论框架：数学文化融入教科书的内容主要有“数学的形成和发展”“数学在人类文明中的贡献和意义”“数学的人文价值”“中华民族数学成就”4类；数学文化融入教科书的方法主要有“片段式”“旁注式”“问题式”“短文式”4种．通过数据分析和案例分析，可以发现基于此理论框架的2019版高中教科书，初步实现了内容和方式融入的较为均衡的整体分布，并且特别关注了数学文化学习的活动性、传递数学文化的情感温度、展现传统数学的特点等

数学文化；教科书融入；数学文化融入内容；数学文化融入方法

在21世纪初的基础教育改革中，《普通高中数学程标准（实验）》（2003）首次将数学文化与数学探究、数学建模并列为高中数学课程内容，意在通过数学文化让学生受到优秀文化的熏陶，感受数学的科学价值、应用价值、人文价值，领会数学的美，并列出了19个数学文化选题[1]．十几年后，《普通高中数学课程标准（2017年版）》进一步指出了数学文化的内涵，并强调将数学文化融入数学课程，在日常学习中结合相应的数学知识渗透数学文化，提升学生的科学精神、应用意识和人文素养[2]．

作为课程内容重要载体和教学重要资源的教科书，如何实现数学文化的融入？数学文化既包含数学的思想、精神、语言、方法、观点，以及它们的形成和发展；还包括数学在人类生活、科学技术、社会发展中的贡献和意义，以及与数学相关的人文活动[2]．由此可见，数学文化的内容是非常广泛的，甚至有点包罗万象．对于教科书而言，有益之处是素材丰富，不利之处是容易泛化．特别是对于中学教科书，数学文化是一种融入，而不是一本数学文化教材，因此首要的问题就是融入教科书的数学文化内容，如何选择，选择什么？当融入的内容确定后，接下来的问题就是这些内容以何种方式融入，才能让数学文化和数学知识的学习浑然一体？历经三版教科书[3-5]，20年的编写研究，初步构建了数学文化融入教科书的理论框架，即数学文化融入教科书的内容与方法．

1 数学文化融入教科书的内容

1.1 内容选取原则

文化植根于人类心灵深处，是长期的历史积淀[6]．因此，融入教科书的数学文化内容，无论是思想、方法、观点还是精神和价值，不再包罗万象，而是根据中学数学主题特点，具有一定的“历史性”，即有一种时间发展的线索，反映出文化的“长期历史积淀”的特点．例如一个具有购物情境的问题就不是数学文化内容的选择，而一个弦图情境的问题则是数学文化内容的选择．

当然，除了这种基于“文化”本身特点的历史性原则外，还要考虑到教科书的编写研究是一个系统，这个系统往往划分为知识内容和特色主题两类研究，而数学文化属于特色主题类，特色主题之间虽然无法避免交叉，但是追求交集最小化．例如问题情境主题和数学文化主题（人教版教科书的教科书前期编写研究特色主题一般有问题情境、数学文化、训练系统、信息技术等），情境中的科学技术类在一定程度上也可以看作数学文化中的科学价值内容，为了避免交叉，数学文化在科学价值内容选择上就会更加注重具有历史性的情境．

1.2 内容条目及具体表现

通常，数学文化的内容包括数学与数学、数学与生活、数学与科技、数学与人文艺术4个方面．在“历史性”原则基础上，从这4个方面的数学文化中，结合中学数学的课程目标、知识内容及特点，选择了4种融入教科书的数学文化内容条目：（1）数学与数学、其它对数学的作用，这些构成了“数学的形成与发展”这个内容条目；（2）众所周知，数学的工具性、方法性，使它成为了科学的语言，成为了人们认识世界和改造世界的工具，因此构成了“数学在人类文明中的贡献和意义”这个内容条目；（3）数学的人文价值，既包括纯粹数学的美，也包括创造它的数学家的精神以及数学本身的精神，还包括数学与人文艺术的互动，特别是哲学、美术、音乐等，这些构成了“数学的人文价值”这一内容条目；（4）与一般图书不同的是，教科书本身承担着传播本民族优秀传统文化的责任，因此将“中华民族数学成就”单独作为一个内容条目．图1直观表明了融入教科书的数学文化内容与通常的数学文化内容之间的关系（由于数学的形成与发展、中华民族数学成就的内容均关注了4种关系，所以为了避免图1中线条过密，采用从旁边引线方式）．

对于每一条内容条目，再次细分，抓重点，明确了这些内容具体表现在哪些方面，以增强融入教科书的数学文化内容选取时的操作性，这样就形成了融入教科书的数学文化内容的二级分类表（表1）．

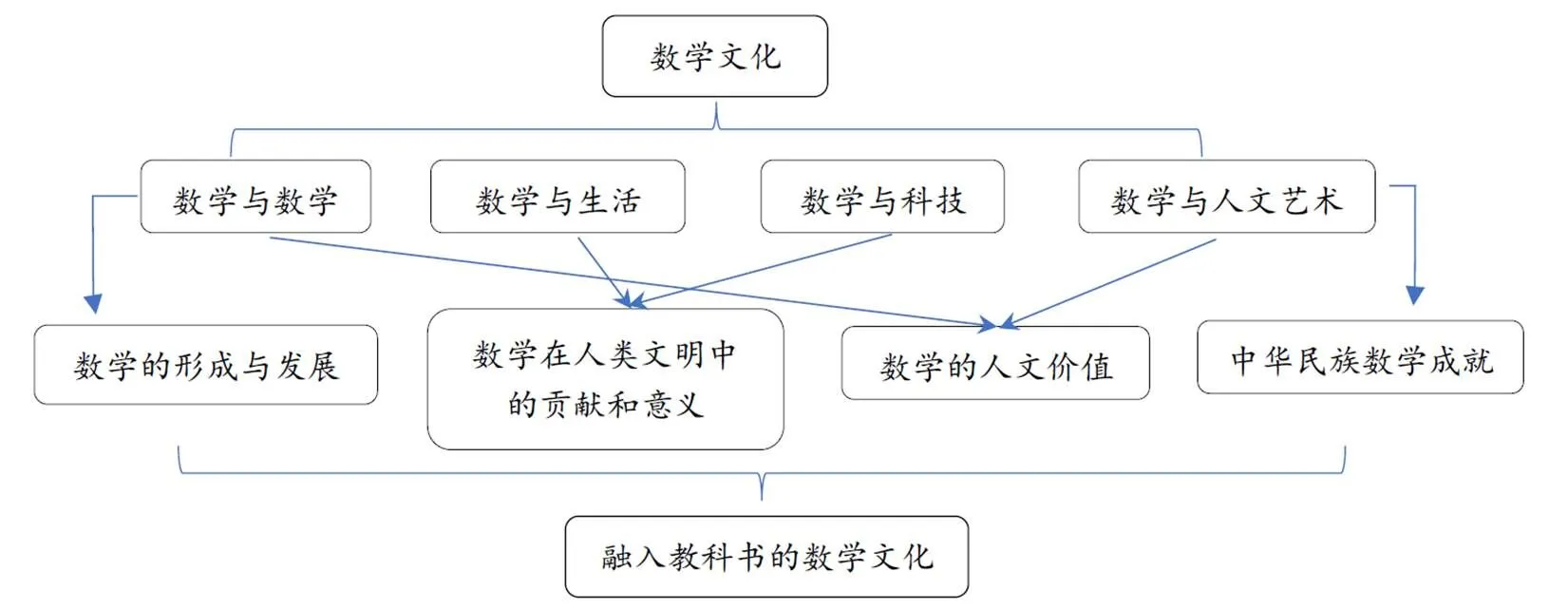
图1 数学文化与融入教科书的数学文化

表1 融入教科书的数学文化内容条目及具体表现

2 数学文化融入教科书的方法

2.1 内容融入原则

知识是文化的载体，没有知识，就没有文化[7]，可以说知识本身的学习就蕴含着数学文化的渗透．从这个角度，在知识讲解中，字里行间可以充满这个数学主题所蕴含的数学文化，这是数学文化在教科书中的一种隐形融入，即以数学知识为呈现焦点，兼顾数学文化；而这里所探讨的是数学文化在教科书的显性融入，即以数学文化为呈现焦点，数学知识为载体，即教科书的一个问题、一个栏目、一个题目、一段文字的呈现角度是“数学文化”，而非“数学知识”．

此外，教科书的载体特点是容量有限，它受知识量、课时、学生负担、定价等多种主客观因素制约．因此对于没有专门课时配比的数学文化，融入方式多样化尤为重要，即充分利用教科书空间，灵活地呈现数学文化内容．

2.2 数学文化融入的方法

基于“显性化”和“多样化”原则，设计了4种数学文化的融入方式：（1）片段式，通常是一段融入知识讲解的文字，适于表现数学形成的动力或数学发展中的关键节点；（2）旁注式，通常是以小贴士的形式搭配在相应的知识讲解旁边，适于表现数学文化中的一些特色元素，如数学符号、数学家简介、典籍等；（3）问题式，通常是栏目问题、例题或习题，适于表现数学发展中的著名问题和方法，以及数学发展的规律；（4）短文式，适于表现某一数学分支的形成与发展、数学在人类文明中的贡献和意义、数学的人文价值等这些宏观内容．

由此可以看出，从数学文化融入的内容到融入方式，结合其所处的教科书位置，是一个整体的设计．这3者之间有一定的对应性，即尽量做到一定的位置出现一定的呈现方式，一定的呈现方式展现一定的内容，一定的内容承载一定的数学文化作用，做到有的放矢，呈现出一定的层次（如表2所示）．

表2 “作用”“内容”“方法”的关系

3 高中教科书（2019版）中数学文化的分布与 案例分析

教科书的编写研究是一个继承与创新的过程，数学文化这个特色主题的研究也是如此，继承于数版教科书中的数学史融入研究，创新于2004版高中教科书，从数学史到数学文化．历时三版教科书前期研究，两版教科书的使用，搭建起了较为完整的理论框架，如今也已应用于2019版高中教科书的编写．下面就以2019版高中教科书为例，从数学文化分布和案例分析两个角度探讨理论框架的编写实现．

3.1 数学文化的分布

通过对表1和表2编码，统计了高中教科书（2019版）5册的数学文化内容与方法数量．从内容与方法的“类”分布和“册”分布两个角度梳理和分析数据．

3.1.1 内容与方法的“类”分布

全套书中共有70处融入了数学文化，4种融入方法的占比如图2所示，其中占比最大的是短文式，37%；最小的是片段式，17%．相对而言，还比较均衡．短文式最多，可能与这种方式既能综合表现数学文化不同条目，也能充分展开数学文化内容有关；片段式最少，可能与选取数学文化内容插入知识讲解后实现浑然一体的难度较大有关．

图2 数学文化的融入方法

在每一处，一种融入方式所承载的数学文化内容条目可能不止一种，因此全套书共有103个数学文化内容，4种数学文化内容条目的占比如图3所示．可以看到，内容条目分布不均衡，“数学形成与发展”占比高达51%，“数学的人文价值”占比只有13%．这可能与不同内容条目的素材丰富、融入方式是否多样有关（如表2），不过可能也和数学文化进入教科书时间短，某些内容条目开发积累的素材少有关，如人文价值条目．虽然“中华民族数学成就”占比也才11%，但是考虑到这个内容能同时容纳其它条目，但是其它条目无法容纳它，所以这个占比还是充分说明了高中教科书对于传播数学传统文化的重视．

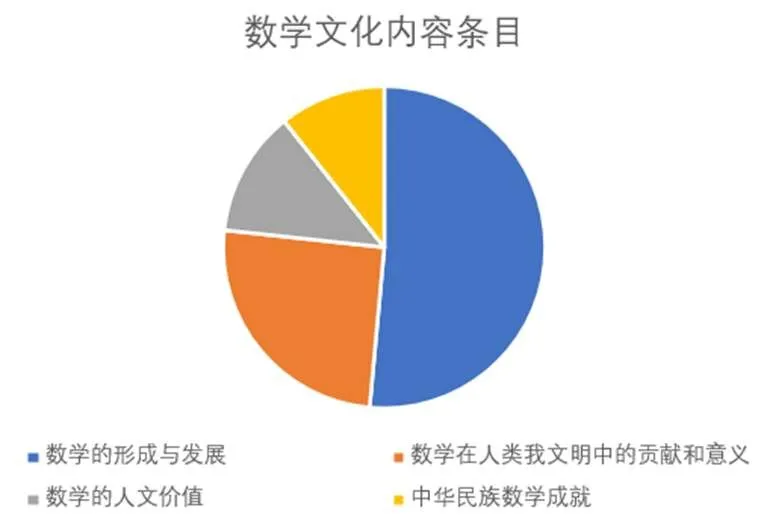
图3 数学文化内容条目

3.1.2 内容与方法的“册”分布

从图4和图5，可以看到各册教科书在数学文化融入内容与方法上的分布与差异．必修1在“数学在人类文明的贡献和意义”中占比最大；必修2在“数学的形成与发展”中占比最大；选择性必修1在中华民族数学成就中占比最大；选择性必修2只有“数学的形成与发展”比较突出；选择性必修3在“数学的人类价值”上有所缺失．与融入内容相比，融入方法的差异更大一些，特别是“旁注式”和“问题式”，必修2的旁注式最多，选择性必修1无；选择性必修2的问题式最多，必修2和选择性必修1无．这种分布的差异，可能和每一册知识内容的主题有关，比如选择性必修1的内容为立体几何和解析几何，选择性必修2的内容为数列和微积分，相比于前者，数列的经典问题丰富，易于设计成例题和习题用“问题式”融入．

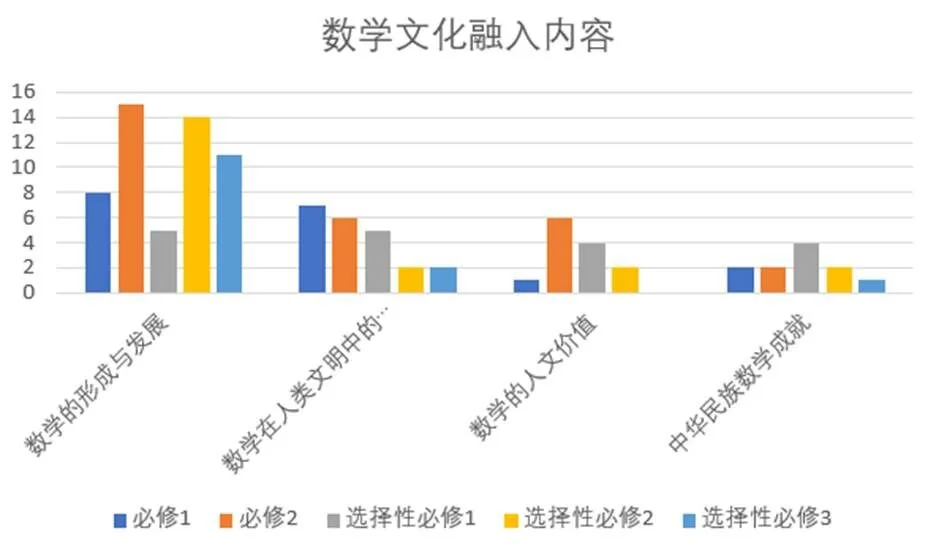
图4 数学文化融入内容

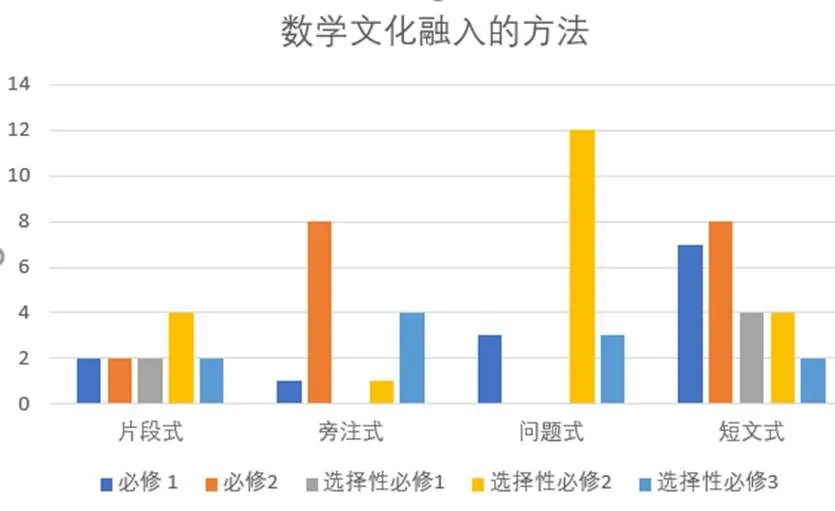
图5 数学文化融入的方法

总的来说，数学文化已经成为教科书的一部分，高中教科书（2019版）平均每两个课时就有一处显性的数学文化融入．而且，数学文化融入的内容涵盖了每一种内容条目及条目的具体表现，其中融入最多的是“数学的形成与发展”，也融入了一定数量的“中华民族数学成就”，偏少的是“数学的人文价值”．与融入内容条目的较大差异相比，从全套书来看，数学文化融入方式的分布就更加均衡，较多采用的是“短文式”；不过每一册的4种融入方式差异还是较大的，特别是必修2和选择性必修2，前者“旁注式”占比42%，后者“问题式”占比57%．

3.2 案例分析

与以往教科书相比，数学文化理论框架的构建除了使2019年版高中教科书的数学文化融入更具有系统性外，还针对性地开发了一些别具特色的数学文化融入案例．例如，增加数学文化学习的活动性，传递数学文化的情感温度，展现传统数学的特点等．

3.2.1 主题学习：在活动中提升素养

2019年版高中教科书中最具特色的数学文化融入就是选学栏目“文献阅读与数学写作”，这是一个数学文化主题学习活动．全套教科书一共有4个主题活动：函数的形成与发展、几何学的发展、解析几何的形成与发展、微积分的创立与发展．每一个主题都是围绕一个分支或核心概念，让学生通过一系列的自主活动，了解它们的形成与发展，领悟数学发展的动力、数学运行的规律，以及数学在人类文明中的贡献和意义等．教科书呈现都是从明确主题学习目标开始，然后给出实施建议和参考选题，并要求以“论文”形式呈现和交流主题学习结果．

对于第一个出现的“函数的形成与发展”，特意给出了“文献综述的结构”，让学生明确如何通过文献阅读进行写作；对于这4个主题活动，虽然都是“形成与发展”，但其承担的数学文化内容远远超越了“形成与发展”，4个主题活动的参考选题都包含了“形成与发展”“数学家”“对人类文明进步的贡献”等方面．因此，这种综合性高、活动性强的数学文化主题活动，不仅有助于让学生了解数学、认识数学，体会到数学及数学家的精神，还有助于学生看到数学与人类文明的关系，真正地站在文化的角度看数学，提升自身的数学素养与文化素养．

3.2.2 习题：在问题解决中提升能力

在以往的教科书中，学生多以“阅读”的方式学习数学文化，融入方式基本上采用“短文式”．在研究基础上，融入方式逐渐多样化，比如上面的主题学习，就是一种“大活动”，除此之外，“问题式”就是一种“小活动”，意在让学生学习数学文化的方式操作性更强一些．这种融入方式一是选取一些典型问题或方法编制成教科书例题或习题，二是将某一个概念、定理或公式的发展与问题解决结合起来编制成例题或习题，让学生在问题解决中感悟数学文化、提升能力．

如图6所示是二项式定理中的一道数学文化题目[8]，意在让学生通过自己细化和完善二项式定理的发展脉络图，感受到：（1）数学的整体性．如二项式定理的“数”“形”特征，以及对不同数学分支（算术、几何、概率、组合数学）的联结作用，就像英国数学家德·摩根所言：“一个数学家需要知道不同数学分支中的发明过程，他需要明白牛顿是在沃里斯已经给出的更高等定理提示下才发明二项式定理的．”（2）数学的文化性，某一个命题或公式的发展完善，可能需要几百甚至几千年，从中既能看到不同时期数学的特点和局限，也能看到数学发展和人类文明的互动．

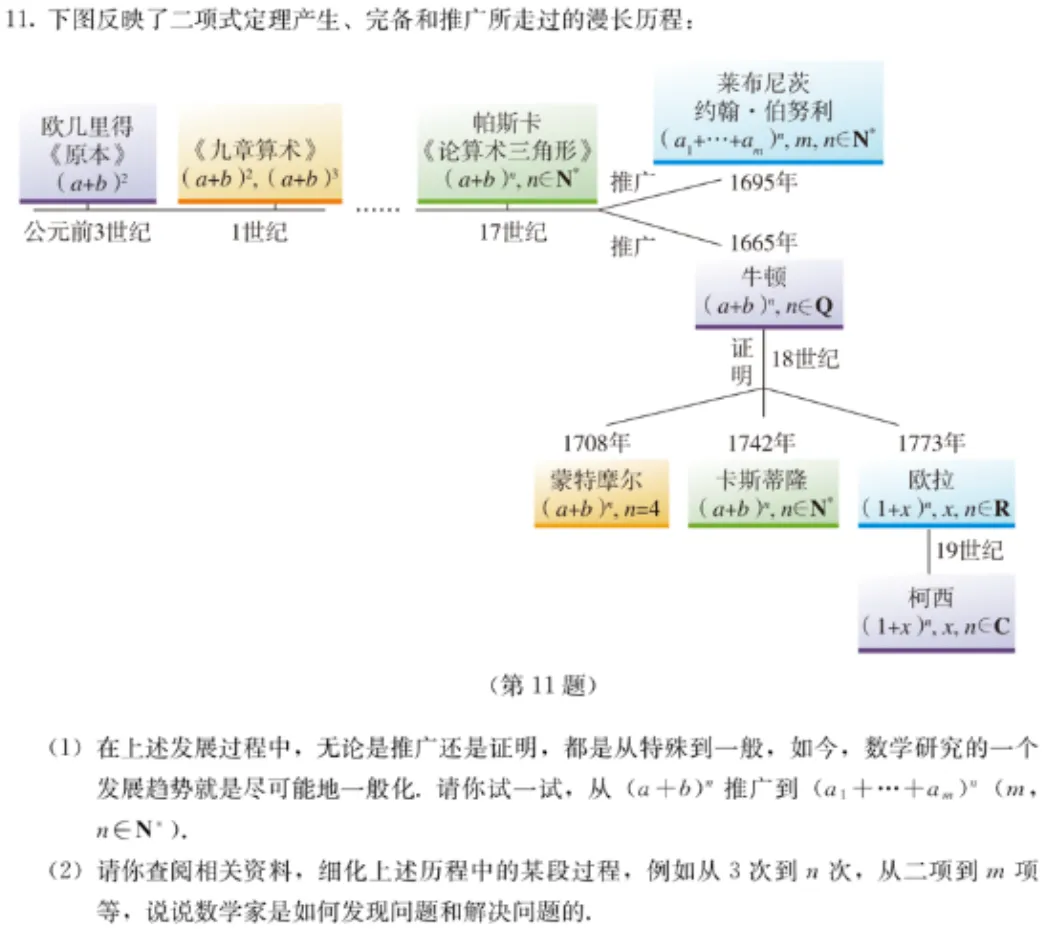
图6 二项式定理数学文化题目

3.2.3 小结：在数学文化特有的温度中感受精神

对于数学文化的融入，或许最自然的一种状态是与知识的学习浑然一体．于是提出了“片段式”，无论是在一章的引言、小结，还是在知识的讲解中，都能以这种方式融入数学文化．不过，这可能也是所有融入方式中难度最大的一种，特别是做到“浑然一体”．相比于之前教科书的“零星”状态，“片段式”的融入方式已经在2019年版高中教科书占据了一定的比例，而且有一些片段融入质量颇高．例如在“复数”的章小结中，有这样一段话：

在数学史上，从古希腊丢番图时代人们求一元二次方程的解时发现复数问题开始，……再到18世纪末韦塞尔给出复数的集合表示，人们才开始接受复数，这是一个漫长而曲折的过程，其中充满着数学家的想象力、创造力，表现了数学家不屈不挠、精益求精的精神．……显示了人类理性思维的强大作用[9]．

这段话充满了数学文化特有的情感温度，能让学生有一种情感上的认同感，复数概念的探索是漫长的，就如同自己的数学学习之路一样；同时在这种情感认同与知识总结中，又能感受到数学家的精神和数学的理性精神．

3.2.4 短文：跨越古今领悟传统之美

中国传统数学源远流长，有其自身特有的思想体系与发展途径，也有其固有特色[10-26]，如构造性、机械化以及离散型的算学形式等[27]．由前面的数据分析可以看到，2019版高中教科书注重传统数学文化的融入，有杨辉三角、高次方程算法、祖暅原理、秦九昭“三斜求积”“吴方法”“垛积术”以及各种古算题等，非常有利于实现教科书“培根铸魂”的教育目标．其中，颇具特色的是一篇跨越古今的短文：坐标法与数学机械化[28]．

这篇短文通过“笛卡儿通过坐标法将几何问题转化为代数方程求解——莱布尼茨提出机器可以成为推理工具思想——王浩提出走向数学机械化——吴文俊提出机器证明的吴方法——吴方法与中国古代方程算法的渊源”，从历史角度概述数学机械化发展的同时，聚焦于“吴方法”及其思想来源之一——中国古代解方程的计算方法，由今追古，让学生领略到传统数学的特色，又由古至今，让学生看到这种特色带来的启示，以及由传承而来的新发展．

4 结束语

从最初的一个提议到将数学文化作为一个教材编写研究的主题，从一个个素材的选择到数学文化融入教科书的理论框架初建，数学文化融入教科书的编写研究虽已初具形态，从数据分析和案例分析可以看出，既实现了融入的整体分布，也实现了特色案例的融入．但是从起步到成熟，还需要未来持续的探索与研究，特别是高中教科书（2019版）数据分析中呈现出的一些问题，以及后继教科书的使用跟踪与调查，即课堂教学实践数据的收集和分析等，都为未来数学文化融入教科书的编写研究提供了方向和思路．

[1] 中华人民共和国教育部．普通高中数学课程标准（实验）[M]．北京：人民教育出版社，2003：4．

[2] 中华人民共和国教育部．普通高中数学课程标准（2017年版2020年修订）[M]．北京：人民教育出版社，2020：5．

[3] 人民教育出版社课程教材研究所中学数学课程教材研究开发中心．普通高中课程标准实验教科书数学（A版）[M]．北京：人民教育出版社，2004：整体引用．

[4] 人民教育出版社课程教材研究所中学数学课程教材研究开发中心．义务教育教科书数学[M]．北京：人民教育出版社，2012：整体引用．

[5] 人民教育出版社课程教材研究所中学数学课程教材研究开发中心．普通高中教科书数学（A版）[M]．北京：人民教育出版社，2019：整体引用．

[6] 徐利治．数学文化教养对人生的作用[J]．教育研究与评论（中学教育教学），2014（1）：5．

[7] 杨叔子．数学很重要 文化很重要 数学文化也很重要——打造文理交融的数学文化课程[J]．数学教育学报，2014，23（6）：6.

[8] 人民教育出版社课程教材研究所中学数学课程教材研究开发中心．普通高中教科书数学选择性必修第三册（A版）[M]．北京：人民教育出版社，2020：35．

[9] 人民教育出版社课程教材研究所中学数学课程教材研究开发中心．普通高中教科书数学必修第二册（A版）[M]．北京：人民教育出版社，2019：93．

[10] 严卿，喻平．初中生逻辑推理能力的现状调查[J]．数学教育学报，2021，30（1）：49-53．

[11] 李杰民，廖运章．条件概率的本质及其教学建议[J]．数学教育学报，2021，30（1）：54-60．

[12] 邓海英，严卿，魏亚楠．数学情境问题解决错误分析与评价[J]．数学教育学报，2021，30（1）：61-67．

[13] 马淑杰，张景斌．高中学生数学原有知识水平和学习认知负荷对数学课堂学习效率的影响研究[J]．数学教育学报，2021，30（2）：26-31．

[14] 伍春兰．PDSA视域下基于教师学习的中学数学课例研修研究[J]．数学教育学报，2021，30（3）：78-82．

[15] 栗小妮，汪晓勤．HPM课例研究对教师MKT的影响[J]．数学教育学报，2021，30（3）：83-89．

[16] 李健，李海东．情境在现实问题解决中的作用——基于5套人教版初中数学教科书的纵向比较[J]．数学教育学报，2021，30（4）：30-34．

[17] 斯海霞，孔梦蝶，叶立军．初中生活数学类拓展性课程课堂数学活动特征研究——基于名师教学视频分析[J]．数学教育学报，2021，30（4）：35-40．

[18] 喻平，董林伟，郭庆松．中学生数学品格与价值观的问卷设计[J]．数学教育学报，2021，30（4）：12-18．

[19] 吕松涛，曹广福．高中向量教学中数学思想的渗透[J]．数学教育学报，2021，30（4）：19-24．

[20] 武丽莎，朱立明．高中数学学科核心素养：生成机制与培养路径[J]．数学教育学报，2021，30（4）：25-29．

[21] 章飞，俞梦飞，顾继玲．初中数学教科书中概念的呈现方式及一致性研究[J]．数学教育学报，2021，30（5）：21–27．

[22] 于文华，王光耀，蔡金法．基于BEA的个体问题解决干预有效性研究[J]．数学教育学报，2021，30（5）：28–32．

[23] 张龙军，熊莉莉，张景中，等．教育数学在农村初中首轮实验的探索与思考——“重建三角”在成都市青白江区祥福中学实验分析[J]．数学教育学报，2021，30（5）：33–38．

[24] 王海青，曹广福．从《原本》谈中学平面几何课题式教学研究[J]．数学教育学报，2021，30（5）：39–46．

[25] 崔志翔，杨作东．义务教育阶段一个数学核心素养的评价框架[J]．数学教育学报，2021，30（5）：47–52．

[26] 姜文，严虹，夏小刚，等．高中生数学学习态度的调查研究——基于贵州省的调查数据分析[J]．数学教育学报，2021，30（5）：53–57．

[27] 吴文俊．中国数学史大系（第一卷上古到西汉）[M]．北京：北京师范大学出版社，1998：1．

[28] 人民教育出版社课程教材研究所中学数学课程教材研究开发中心．普通高中教科书数学必修第一册（A版）[M]．北京：人民教育出版社，2019：89．

The Content and Method of Integrating Mathematical Culture into Middle School Textbooks

WANG Rong

(People’s Education Press Curriculum and Teaching Materials Research Institute, Beijing 100081, China)

The integration of mathematical culture into textbooks determines the realization of the objectives of mathematical culture curriculum and classroom teaching to a certain extent. After three editions of textbook compilation research, the theoretical framework for integrating mathematical culture into textbooks has been initially constructed: The contents of mathematical culture integrated in textbooks mainly include four categories: “formation and development of mathematics”, “contribution and significance of mathematics in human civilization”, “ humanistic value of mathematics” and “ mathematical achievements of the Chinese nation”. There are four main methods for integrating mathematical culture into textbooks: “fragment”, “marginal note”, “question” and “short essay”. Through data analysis and case analysis, it can be found that the 2019 edition of high school textbooks based on this theoretical framework has initially achieved a relatively balanced overall distribution of contents and methods, and paid special attention to the activity of mathematical culture learning, the emotional temperature of mathematical culture, and the characteristics of traditional mathematics.

mathematical culture; textbook integration; mathematical cultural integration contents; mathematical culture integration methods

方面．

G632

A

1004–9894（2022）01–0019–05

王嵘．数学文化融入中学教科书的内容与方法[J]．数学教育学报，2022，31（1）：19-23．

2021–11–04

教育部人文社会科学青年基金项目——我国中小学课堂教学质量评价模型的构建与应用研究（19YJC880145）

王嵘（1978—），女，河北邢台人，副编审，硕士，主要从事数学课程教材教法研究．

[责任编校：周学智、张楠]