金属线胀系数测量实验装置的设计与制作

郭 磊，王美迪，鄢 嫣，姚 平

(长江大学 物理与光电工程学院，湖北 荆州 434023)

线胀系数也被称为线弹性系数，在工程设计、机械制造和新材料应用等方面都有重要应用，因此在大学物理实验中线胀系数的测量占有重要的地位，其中金属线膨胀系数的测量是很多高校所开设的必修实验项目.目前金属线胀系数主要的测量方法有：光干涉法测量[1,2]和千分表测量[3]，其中光干涉法存在干涉条纹不易读取，光路调节复杂等缺点，而千分表反复使用极易磨损.另外在测量过程中，由于被测试件加热不均匀会带来较大的误差.为了更好的开展金属线胀系数测量的实验，笔者根据多级光杠杆产生灵感[4,5]，设计并制作了一款采用水浴加热的金属线胀系数测量装置，随后开展了长达数月的实验测试，结果证明该装置使用效果良好，非常适合大学物理实验教学.

1 实验装置的构造与原理

作者设计与制作的实验装置主要由物理杠杆模块、电加热模块、光杠杆模块以及支架模块构成，如图1和图2所示，图1为实验装置的实物图，图2为实验装置的模型图.核心模块为光杠杆模块，该模块主要由K9光学反射镜、光源、望远镜、钢尺等器件组成.支架模块主要由木板、直角固定器和合叶等组成.电加热模块主要由石英玻璃加热水管、温度传感器、电加热棒、水泵、水管、待测金属杆固定组件等组成.物理杠杆模块则是由金属物理杠杆、弹簧和弹簧固定组件组成.该仪器的主要作用是教学演示，可以测量金属杆的线胀系数，进而计算相对误差、不确定度等.

图1 实验装置图

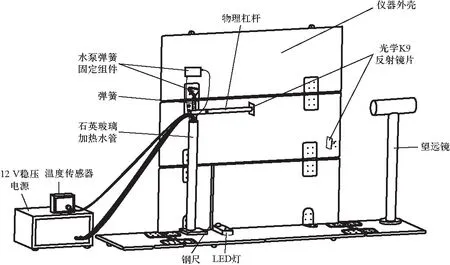
(a) 实验装置模型图展开状态

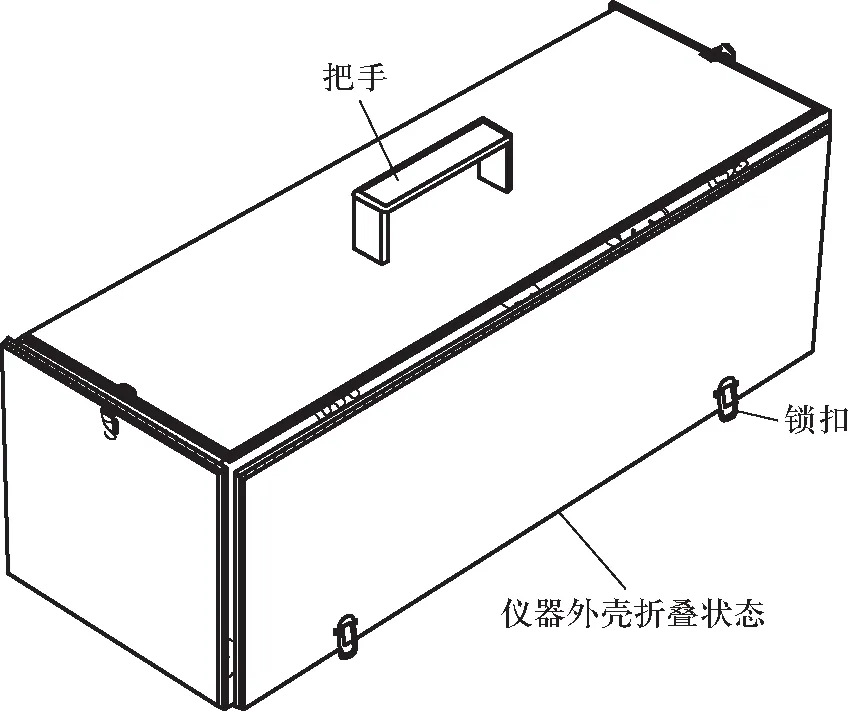
(b) 实验装置模型图折叠状态

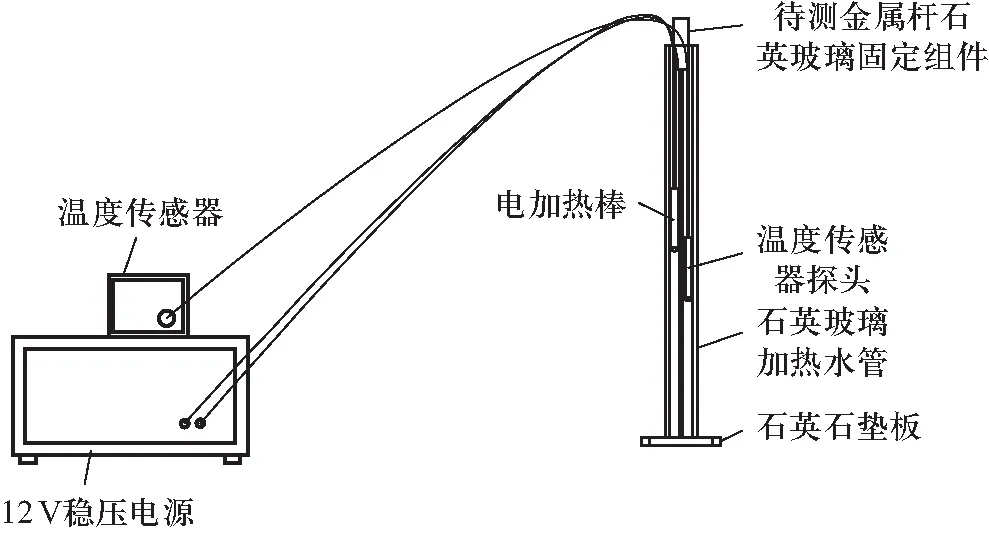
(c) 实验装置模型图加热模块

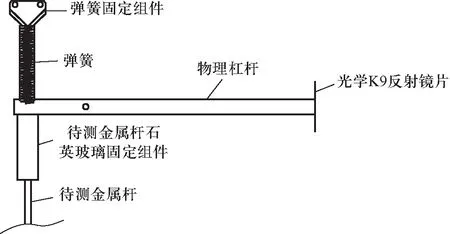
(d) 实验装置物理杠杆模块构造图2 实验装置模型图

金属的热膨胀变化量与温度可近似认为是线性相关的，但它是一个非常微小的变化量，无法用肉眼观察且不易测量.本仪器利用电加热棒对待测金属杆进行水浴加热，同时利用水泵实现水循环，用2个温度传感器分别插入水管的底部和顶部，观测水温变化.如图3所示，用物理杠杆设置一定放大倍率，一端与待测金属杆相抵住，另一端固定一个反射镜片A，在右侧设置一个望远镜，对此镜片进行观测. 在反射镜片A右下方固定另一个反射镜片B，在反射镜片A下方置一个刻度尺，经过两次反射，使可以在望远镜中看到钢尺的刻度值.

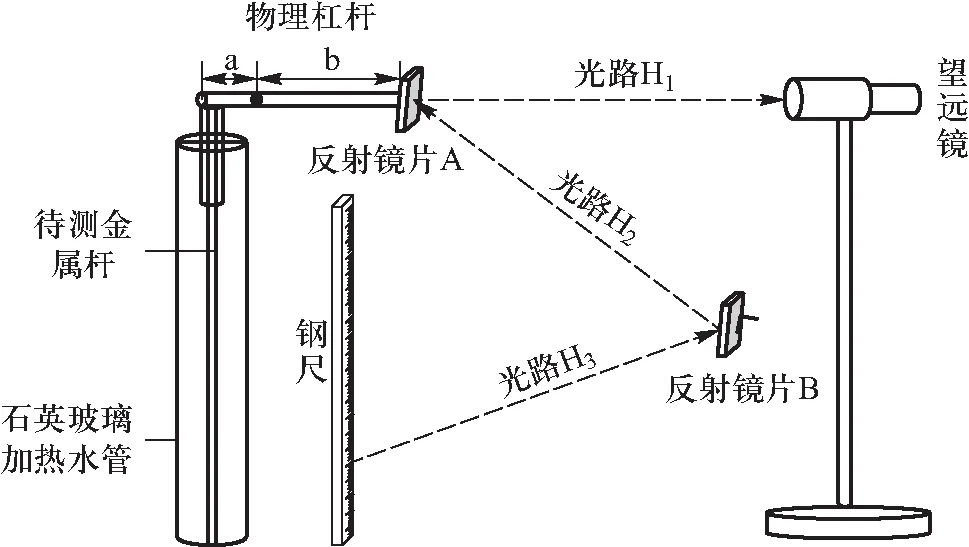
图3 放大倍数原理图

金属杆受热膨胀，发生微小的形变，带动物理杠杆旋转一定的角度，进而带动光杠杆的光路发生一定角度的偏转，经过物理杠杆和光杠杆结合放大，可以用望远镜观测到刻度尺上准确的刻度变化. 当温度升高至T1(℃)时，记录此时的刻度值，当温度升高至(T1+10)℃时,再次记录刻度值，利用温度差和刻度差计算出待测金属的线胀系数.通常重复进行5次实验取平均值即可得到较为精确的线胀系数.

2 金属线胀系数测量实验

2.1 线胀系数测量过程

2.1.1 仪器调整

向石英玻璃加热水管中加入适量的水，将电加热棒、温度传感器和待测金属杆样品依次放入石英玻璃加热水管中，连接好电加热棒与水泵的电源(12 V直流稳压源)，固定好物理杠杆，打开光源，将望远镜调整到合适的位置，能够清晰地看到钢尺的刻度即可.

2.1.2 确定放大倍数

如图3所示，用刻度尺量出支点到待测金属杆受力点的距离a，再量出物理杠杆的支点到反射镜片A的距离b，则物理杠杆放大倍数为

(1)

计算光杠杆的放大倍数，用激光测距仪测量出望远镜到反射镜片A的距离H1，反射镜片A到反射镜片B的距离H2，反射镜片B到望远镜中钢尺刻度处的距离H3，令H=H1+H2+H3，则光杠杆的放大倍数为

(2)

实验装置总的放大倍数为

(3)

2.1.3 测量

仪器调整好后，打开电源，仪器开始对待测金属杆水循环加热，实验时室温约为30摄氏度.当水温升高至35摄氏度时，读取此时的温度值T1和刻度值x1；等待水温升高至45摄氏度时，读取此时的温度值T2和刻度值x2；关闭电源，停止加热，等待水温下降至约29摄氏度时重复上述步骤；测量得到5组数据后，关闭电源停止加热，关闭光源，将仪器折叠收起，完成实验，进行数据处理.

2.2 数据处理

根据实验测量，得到了实验装置放大倍数β和5组实验数据，如表1所示，为5组温度与刻度的实测数据.

2.2.1 计算线胀系数

利用得到的5组数据，分别计算温度差与刻度差.进而利用温度差、刻度差与放大倍数三个物理量分别计算出线胀系数，取平均值后即可得到较为精确的线胀系数.

设在温度为T1时金属杆的长度为L1，温度升高到T2时金属杆的长度为L2，伸长量为ΔL,钢尺刻度变化量为Δx，则

(4)

上式中，α为待测金属杆的线胀系数，β为实验装置的放大倍数，L0为待测金属杆在零度时的长度.由式(4)计算线胀系数得

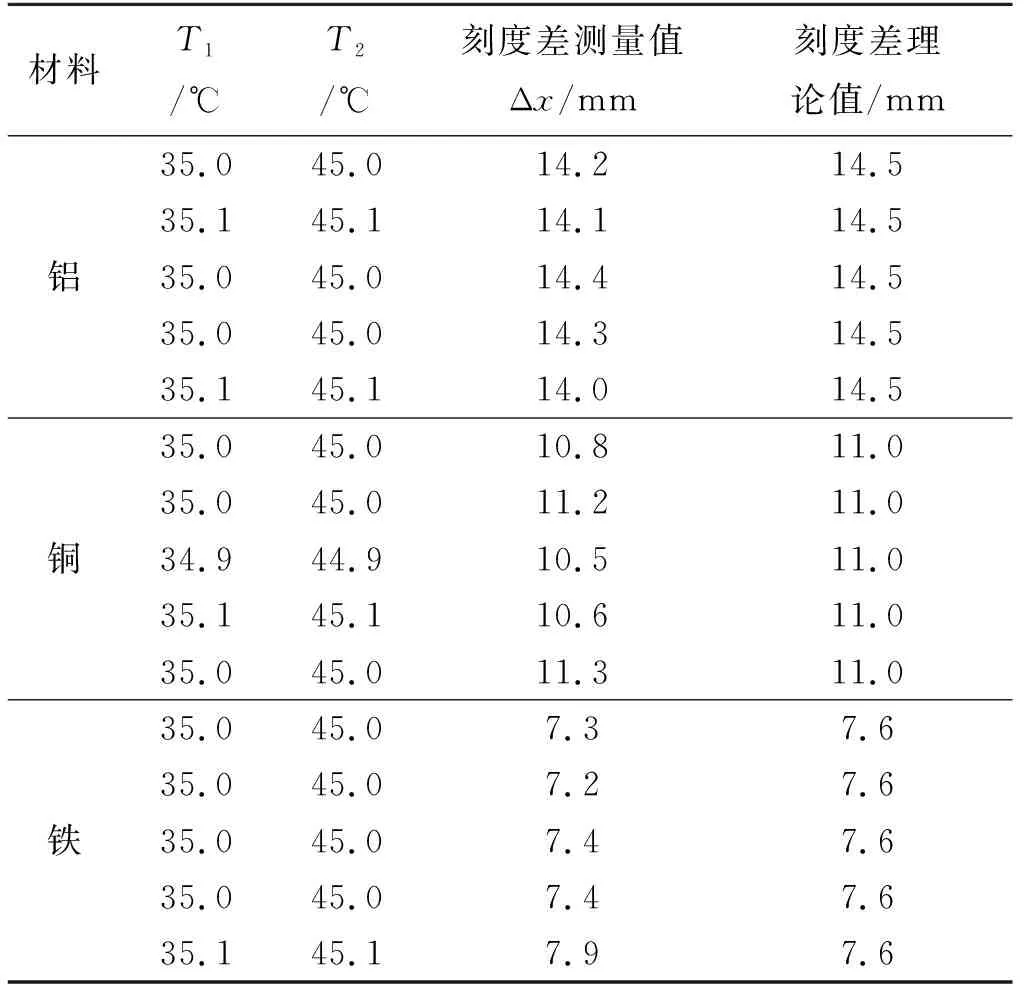
表1 实测数据

(5)

通过取平均值减小误差,则

(6)

2.2.2 计算线胀系数的相对误差和不确定度

(7)

上式中α0为待测金属线胀系数的理论值.

计算线胀系数的不确定度，Δx的A类不确定度为

(8)

上式中，n为刻度差与温度差数据的组数.

Δx的B类不确定度为

(9)

合成不确定度为

(10)

对于光路长度L，物理杠杆支点到待测金属杆受力点的距离a，待测金属杆初始长度L,温度T不考虑A类不确定度，它们的不确定度为

(11)

所以综合不确定度为

(12)

最终得到的结果为

(13)

2.3 典型实验结果

如表1所示，是对实验装置进行实践操作所得到的数据，通过进行数据处理，发现测量结果的误差均在3%以内，计算结果填在了表2中.表2是根据表1实测数据进行数据处理后得到的具体结果.

表2 实测数据计算结果

根据表1的实测数据做折线图，通过4图可以看出，笔者设计与制作的实验装置精确度较高，误差较小，与理论值非常接近.

(a) 铝的实测数据

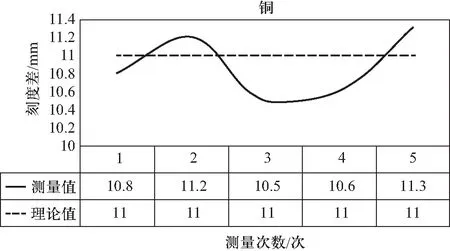
(b) 铜的实测数据

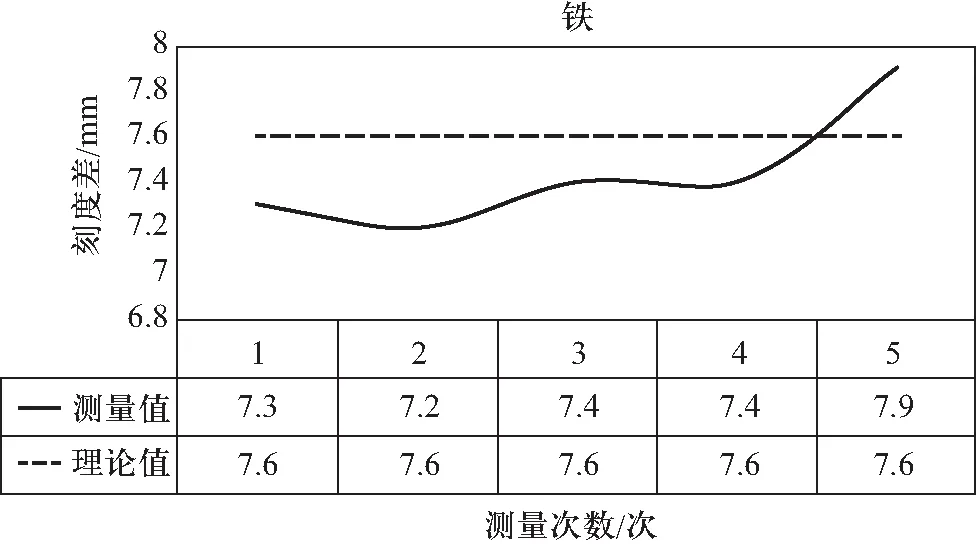
(c) 铁的实测数据图4 实验数据折线图

2.4 误差分析

实验装置的误差来自多个方面，最主要的误差原因是原材料有限，仪器制作不够精密. 待测金属杆的直径是3 mm，热传导也会造成微小的误差. 待测金属杆固定组件和加热水管也会升高一定的温度，但是其材料为石英玻璃，其热膨胀可忽略不计.

3 结束语

通过实验证明，用本装置对金属杆的线胀系数进行测量是可行的，通过物理杠杆与光杠杆结合放大，水循环均匀加热，便携式设计等使得实验现象明显，测量结果准确，光路易于调节，便于携带，适合用于教学演示，比光干涉法、千分表法等方法具有明显的优势，具有一定的发展前景. 本实验可以培养学生的动手能力，掌握和理解热膨胀的原理，并且还紧密联系了光学知识、热学知识，可以加强各学科之间的联系. 笔者设计与制作的实验装置已经申请国家专利，并且将继续优化改进，后续将应用于大学物理实验课程的教学.