各向同性介质的三阶极化率张量元分析

杨国霞，弓文平，刘大禾，石锦卫

(北京师范大学 物理学系 应用光学北京市重点实验室，北京 100875)

非线性光学研究光与物质的非线性相互作用及其所产生的各类非线性光学现象，是光学相关专业学生应当具备的基础理论和专业知识. 极化率张量是非线性光学中最重要的物理量之一，物质的空间对称性导致一些极化率张量元为零，能大大简化极化率的理论处理. 然而，从学生的角度，对称性分析往往是学习的难点，特别是对于不具备群论基础的学生. 从教学的角度，国内外的非线性光学教材中，经常直接照搬极化率张量对称性分析结果，缺乏深刻的讲解. 其中，各向同性介质，特别是各向同性手性介质的三阶极化率张量元的对称性分析就是一个典型的例子.

1 研究背景及问题描述

1.1 研究背景及意义

1.2 问题描述

三阶电极化和电场的关系表达式为[3]

Pi(ωo+ωm+ωn)=

(1)

其中i、j、k、l代指每个场的任意一个笛卡尔坐标分量x、y、z，简并因子D表示3个输入场频率ωo、ωm、ωn的不同排列的数目.为书写方便，用1、2、3分别代表x、y、z，并以i=1时为例来分析，其他类推.

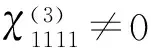
2 基于级联二阶效应的分析方法

由各向同性分布的手性分子组成的介质没有反演对称中心，其所属的对称性类别可以用 ∞∞ 表示，即任意一个方向都是一条无穷重旋转对称轴C∞，但是不存在镜面对称，这样的介质具有6个非零的二阶极化率张量元[4]，分别为

(2)

根据式(2)和级联的二阶效应，即可分析各向同性手性介质中的三阶极化率张量.

为了描述方便，类比教材中的做法[3]，下面用Ej、Fk、Gl分别代表公式(1)中的Ej(ωo)、Ek(ωm)、El(ωn)，并将ωo、ωm、ωn重新记作ωE、ωF、ωG.若有偏振方向分别为1、2的输入场E1、F2，将产生偏振方向为3的极化：

(3)

图1 用级联二阶效应理解的示意图

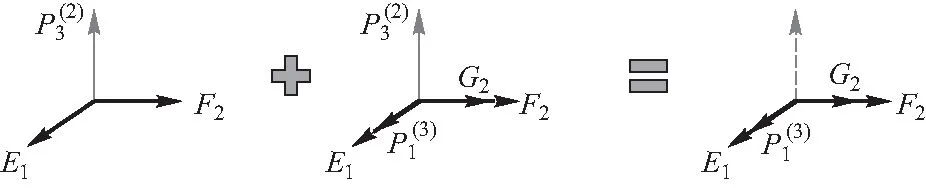
图2 “1122”的级联二阶效应过程示意图

(4)

(5)

图3 “1111”的级联二阶效应过程示意图

3 对称操作法分析三阶极化率张量

对于各向同性介质，三阶极化率张量元是否存在，还可以用对称操作进行分析.例如，假设“1123”的三阶效应存在，则有

(6)

(7)

又因为旋转前后，1′=-1，2′=2，3′=-3，所以

(8)

4 三阶效应对输入场传播方向的要求

在各向同性手性介质中产生二阶效应，除了对输入场偏振方向的要求外，还限制了两输入场的传播方向不能共线[3,4]，根据下述分析，各向同性介质中，三阶效应的产生不需要限制输入场的传播方向.

各向同性的介质中，共有21个非零的三阶极化率张量元，且只有3个张量元独立[1-3,5]，现将其分别记作χA、χB和χC：

χA=yyzz=zzyy=zzxx=xxzz=xxyy=yyxx

(9)

χB=yzyz=zyzy=zxzx=xzxz=xyxy=yxyx

(10)

χC=yzzy=zyyz=zxxz=xzzx=xyyx=yxxy

(11)

xxxx=yyyy=zzzz=χA+χB+χC

(12)

所以，3个输入场E、F、G将会产生电极化：

P(r,t)=ε0D[χA(F·G)E+χB(G·E)F+χC(E·F)G]

(13)

假设输入场为线偏振光，并忽略偏振面由于光学活性产生的旋转，当3个输入场E、F和G的传播方向共面时，定义该平面为相互作用平面(the plane of interaction，简称IP)，将各输入场分解到IP面内和垂直于IP面两个方向：

E=(E‖+E⊥)ei(ωEt-kE·r)+c.c.

(14)

F=(F‖+F⊥)ei(ωFt-kF·r)+c.c.

(15)

G=(G‖+G⊥)ei(ωGt-kG·r)+c.c.

(16)

其中，下标‖表示在IP面内的分量，下标⊥表示垂直于IP面的分量.

不失一般性地，将三个输入场的传播方向固定于笛卡尔坐标系中的xz平面，其中kE沿z方向，kF与kE的夹角为θ1，kG与kE的夹角为θ2，则产生的电极化中，频率为ωE+ωF+ωG的部分为

(17)

其中

P1=ε0D{χAE‖[F‖G‖cos(θ1-θ2)+F⊥G⊥]+

χBF‖cosθ1(E‖G‖cosθ2+E⊥G⊥)+

χCG‖cosθ2(E‖F‖cosθ1+E⊥F⊥)}

(18)

P2=-ε0D{χAE⊥[F‖G‖cos(θ1-θ2)+F⊥G⊥]+

χBF⊥(E‖G‖cosθ2+E⊥G⊥)+

χCG⊥(E‖F‖cosθ1+E⊥F⊥)}

(19)

P3=-ε0D[χBF‖sinθ1(E‖G‖cosθ2+E⊥G⊥)-

χCG‖sinθ2(E‖F‖cosθ1+E⊥F⊥)]

(20)

式中的E‖=|E‖|，F‖=|F‖|，G‖=|G‖|，E⊥=|E⊥|，F⊥=|F⊥|，G⊥=|G⊥|.

为分析所产生的极化是否受输入场传播方向的限制，只写出P+(r,t)的横向分量，因为纵向分量不能耦合到频率为(ωE+ωF+ωG)的场中.P+(r,t)的横向分量即垂直于k+=kE+kF+kG的部分为

P+trans(r,t)=(P‖+P⊥)ei[(ωE+ωF+ωG)t-(kE+kF+kG)·r]

(21)

式中的P‖指P+trans(r,t)位于IP面内的分量，P⊥指P+trans(r,t)垂直于IP面的分量，它们的大小分别为

(22)

P⊥=P2

(23)

其中P1、P2和P3由式(18)—式(20)给出.

由式(18)—式(23)可知，只要输入场E、F和G满足偏振方向的限制，则无论夹角θ1、θ2为何值，所产生的电极化P+(r,t)就总含有横向分量，即各向同性介质中三阶效应的产生，对输入场传播方向无限制.

上述分析是基于3个输入场共面的情况，原则上也可以推广到非共面的情况，但是太过于繁琐，本文不再赘述.

其实，根据公式(13)可以直接进行分析，由于电极化P可以和E、F、G中的任意一个输入场平行，能量守恒和动量守恒总能同时得到满足，对输入场的传播方向kE、kF和kG也就没有限制，这一点和各向同性手性介质的二阶效应完全不同.

5 结论

本文提出了一种级联的二阶效应方法，可对各向同性介质，特别是各向同性手性介质中的三阶极化率张量元是否非零进行快速判断，并能使学生获得简单、直观的理解.本文同样提供了对称操作法的分析思路，但在判断某三阶极化率张量元确为非零时，级联二阶效应方法表现出优越性.非线性效应的产生，除了要求输入场具有一定的偏振方向组合外，输入场的传播方向也同样重要，本文将各向同性介质中所有非零的三阶极化统一于一个矢量表达式，进而分析了三阶效应产生对输入场传播方向的要求，这对于相关的教学科研具有指导意义.