Kagome平面无穷网格上的等效电阻计算

石璐洁，尹鳒凯，鲁 雯，李 丹，李喜彬

(内蒙古师范大学 物理与电子信息学院，内蒙古 呼和浩特 010022)

具有周期结构的无穷大电阻网络曾是世界性难题，Krizysztof Giaro创造性地利用二维傅里叶(Fourier)变换法成功地给出了正方形网格上任意两节点之间的等效电阻[1,2]. 这种方法目前已经被推广到矩形网络[3]、三角网络[4]、六边形网络[5]等. 文献[6,7]分别研究了m×n 阶电阻网络的等效电阻，文献[8]研究了多边形电阻网络的等效电阻. 电阻网络等效电阻的研究已经取得很大进展.

Kagome结构是由三角形和正六边形规则的重复排列构成. 由于其特殊的拓扑性质，一直被凝聚态尤其是拓扑材料等领域所关注[9]. Kagome网络同样具有周期性结构，对于此种网络等效电阻的计算有助于更好地理解它的拓扑性质. 本文利用二维傅里叶变换法计算了Kagome网络结构上任意两点间的等效电阻，并利用Mathematica软件给出了数值结果.

1 无穷格点上等效电阻的计算

为了方便描述此种网格结构，在Kagome平面建立如图1所示的ξη坐标系. 根据 Kagome平面临近格点的排布方式，我们将格点分类，再讨论不同的类型格点之间的等效电阻. 首先定义所有偶数构成的集合E(even)以及奇数构成的集合O(odd). 那么Kagome晶格上的格点可分为A、B、C三类：

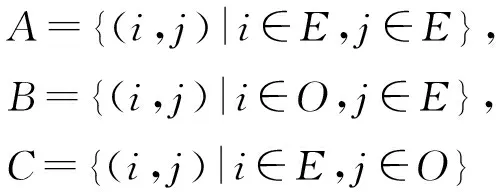
(1)

根据这种分类方式，可以得到如下代数关系.

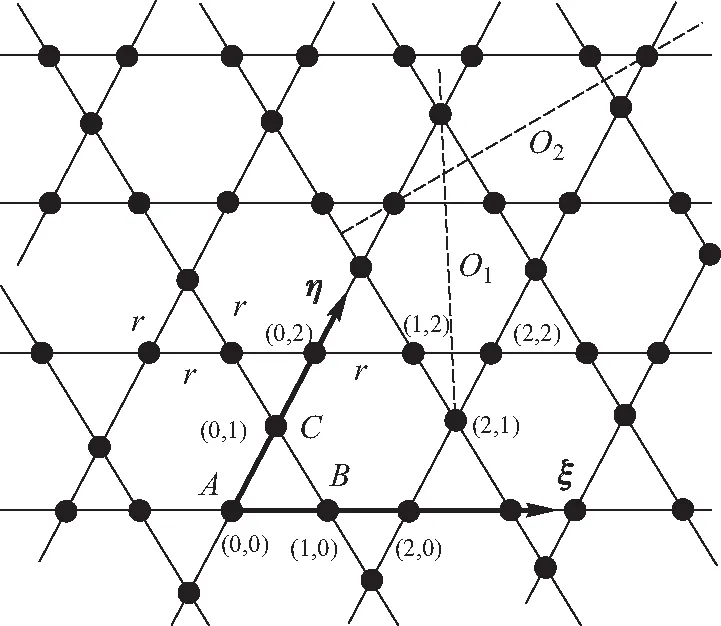
图1 Kagome晶格及其坐标(O1、O2为2个对称轴，r邻近格点之间电阻)

定理1：如果(i,j)∈A,，则(i+1,j)∈B, (i,j+1) ∈C；如果(i,j)∈B，则(i+1,j)∈A， (i+1,j+1) ∈C；如果(i,j)∈C，则(i,j+1) ∈A，(i+1,j+1) ∈B.

为了求得坐标为(a,b),(m,n)的两个节点之间的有效电阻，假设大小为I的电流从(a,b)点流入并从(m,n)点流出，那么电流可以表示为

(2)

其中δij表示克罗内克符号.

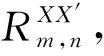
1.1 RAA类型等效电阻的计算

对于此种类型的等效电阻的计算，首先令电流从(0,0)点流入并从(m,n)∈A点流出，则电流可以表示为I(i,j)=Iδi0δj0-Iδimδjn. 由基尔霍夫电流公式[10]，分别考虑通过3类格点的电流，设(i,j)∈A,(k,l)∈B,(p,q)∈C，于是得到以下方程组：

(3)

整理得到

4V(i,j)=rIi,j+V(i-1,j)+V(i+1,j)+

V(i,j-1)+V(i,j+1),

4V(k,l)=V(k-1,l)+V(k+1,l)+

V(k-1,l+1)+V(k+1,l-1),

4V(p,q)=V(p,q-1)+V(p,q+1)+

V(p+1,q-1)+V(p-1,q+1)

(4)

设无穷远处的节点电势为零，定义电势的傅里叶变换为

(5)

则电流的傅里叶变换为

(6)

对A类格点(i,j)∈A进行傅里叶变换:

(7)

即

4F1(x,y)=Ir(1-ei(mx+ny))+2F2(x,y)cosx+

2F3(x,y)cosy

(8)

对于B类格点(k,l)∈B的傅里叶变换为

2F1(x,y)cosx+2F3(x,y)cos(x-y)

(9)

同理，对C类格点(p,q)∈C的傅里叶变换为

4F3(x,y)=2F1(x,y)cosy+

2F2(x,y)cos(x-y)

(10)

联立式(8)—式(10)，解得

(11)

可以通过对F1(x,y)在第一布里渊区上的积分得到(i,j)点的电势 (设无穷远处的节点电势为零):

(12)

于是(0,0)以及(m,n)两点的电势分别为：

(13)

(14)

那么，最终得到相对坐标为(m,n)的2个A类格点之间的等效电阻为

(15)

现在来看2个B类格点之间的电阻. 假设电流从(1,0)点流入并从(m,n)点流出，重复以上的计算过程，得到等效电阻的表达式为

(16)

事实上两个B类格点之间的电阻与2个A类格点之间的电阻彼此等价，这是因为如果(m,n)∈B，则有(m-1,n)∈A. 同理，2个C类格点之间的电阻同样与2个A类格点之间的电阻彼此等价. 因此对于2个相同类型格点之间的等效电阻，只需用式(15)计算即可，不需要再分开讨论.

1.2 RAB类型等效电阻的计算

对于此种情况，假设电流从(0,0)点流入并从(m,n)∈B点流出，则电流的表达式为Ii,j=Iδi0δj0-Iδimδjn. 此时格点电流的傅里叶变换可以表示成

(17)

重复上一节的计算过程，得到关于傅里叶变换后的变量的方程组为

4F1(x,y)=Ir+2F2(x,y)cosx+2F3(x,y)cosy,

4F2(x,y)=-Irei(mx+ny)+2F1(x,y)cosx+

2F3(x,y)cos(x-y),

4F3(x,y)=2F2(x,y)cosy+2F2(x,y)cos(x-y)

(18)

解得

(19)

(20)

利用傅里叶逆变换可以得到两点之间的等效电阻为

(21)

2 数值结果

根据前文的分析，我们是通过X与X′的类型来求得的等效电阻，即如果X=X′则利用式(15)，如果X≠X′则利用式(21). 此为一种角度，另外一种角度则是通过m+n的奇偶性来进行分类：如果m+n=偶数则利用式(15)，如果m+n=奇数则利用式(21). 需要补充的是，对于m+n=奇数的情况，如果n为奇数，需要对m和n交换次序再利用式(21)才能求得正确的等效电阻.

对于式(15)与式(21)这2个二重积分，由于形式较为复杂，无法继续解析求解. 而利用Mathematica编写程序来计算上述积分，就可以得到2种类型下无穷Kagome格点上等效电阻的结果.表1展示了部分计算结果.

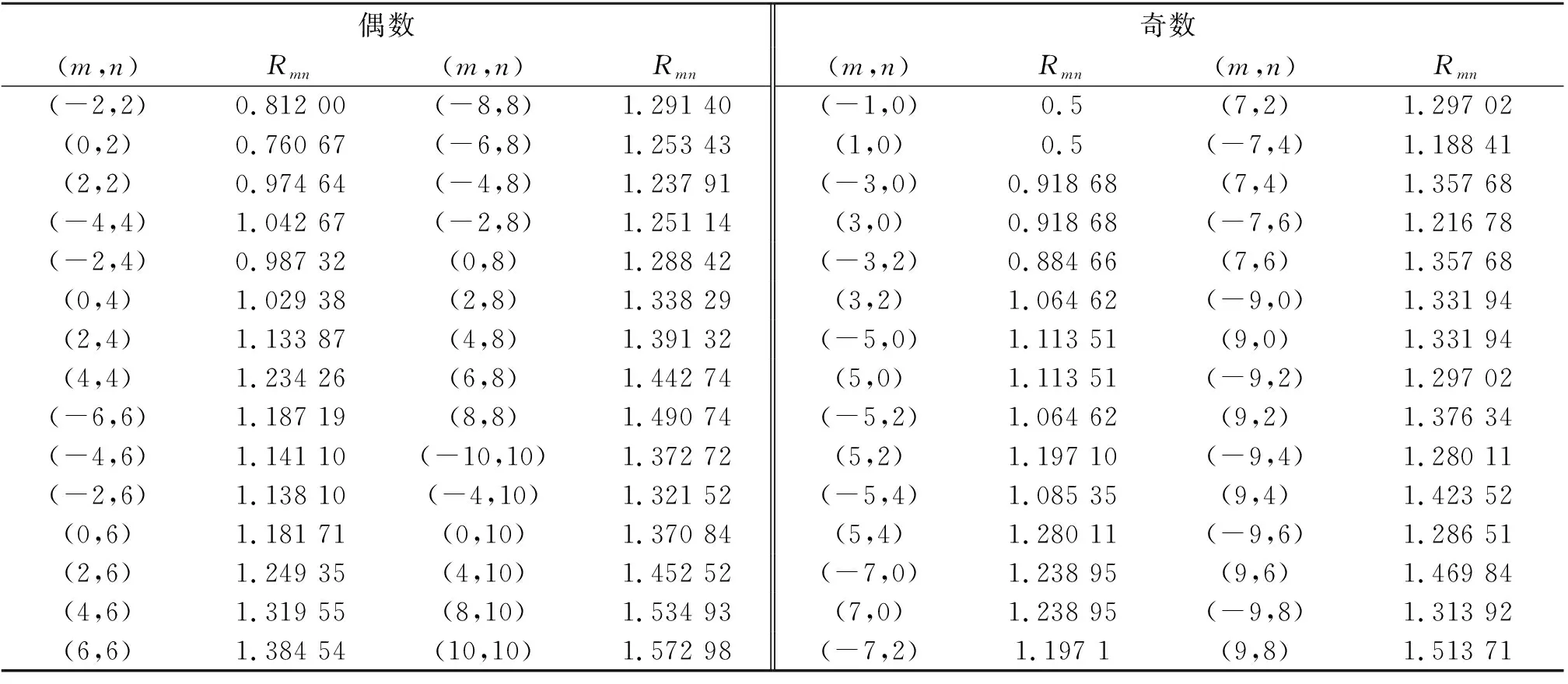
表1 Kagome网格的等效电阻(r=1)

3 总结

本文探讨了Kagome平面无穷等值电阻网格任意两节点间的等效电阻问题. 针对这种特殊无穷电阻网格的特点，本文选取了恰当的坐标系，利用二维傅里叶变换，成功导出了相应的解析式，为第一布里渊区上的二重积分，并利用Mathematica软件给出了数值结果. 数值计算结果与理论数值相符，验证了本文分析的合理性. 本文所探讨内容具有一定的创新意义，对电路的教学同样具有一定的参考价值.