复杂电磁波的动量密度

董正高

(东南大学 物理学院，江苏 南京 211189)

大学物理课程的电磁学、电动力学、光学等相关教学内容中，坡印廷矢量是认识电磁波的一个重要物理量，然而对相关概念的分析并不是很深入.适当拓展、深化相关概念的教学，更好地与当前科研领域相衔接，培养新时代大学生今后走上工作岗位的前沿探索意识和科技创新素质，是当前课程思政教改的重要一环.众所周知，在普通物理的教学中，一般以均匀平面电磁波为例，对坡印廷矢量仅限于较简单地讲解：该矢量对应电磁波的能流密度，其方向就是电磁波传播的方向[1,2]. 相关的教学内容，很直观地让学生认识到坡印廷矢量所反映的电磁波传输的能流特征，也即电磁波具有的纵向传播动量的本质. 不过，对于普遍意义上的复杂电磁波来说，比如近年来引起广泛兴趣的矢量光场[3,4]，结合麦克斯韦方程对坡印廷矢量进行适当的数学推导，就可以发现该矢量除了包含有纵向能流对应的动量之外，还具有横向轨道动量以及一种跟电磁波偏振态相关的内禀能流——自旋动量[5-7].本文基于对坡印廷矢量的分解，从动量的角度对该矢量进行了讨论，重点阐述了几种复杂光场中坡印廷矢量所蕴含的横向轨道动量和自旋动量.

1 坡印廷矢量

在教科书中，坡印廷矢量的定义式为

S(t)=E(t)×H(t)

(1)

对于时变的电磁场来讲，式(1)是含时的瞬态表达式.如果电磁波的频率非常高，比如光波，实际更关心坡印廷矢量的时间平均值.教学中会通过下式来计算坡印廷矢量在一个周期T内的时间平均值：

(2)

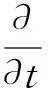
(3)

其中：< >表示取时平值， *表示取复共轭.

坡印廷矢量代表电磁场能流密度，可以反映电磁能量流动的连续性，这一内涵则需从麦克斯韦方程经过简单的数学推导后，由下述微分形式的坡印廷定理表达式体现出来[6,8]：

(4)

(5)

坡印廷定理表明：任意闭合面A上坡印廷矢量的负通量，等于体积内电磁能量的时间变化率与功率损耗之和.显然，体积内电磁能量的单位时间增加量以及功率损耗，来源于单位时间流入体内的电磁能量.因此，坡印廷矢量代表了能流密度.该式体现了电磁能量的守恒特性(能流连续性)，与电荷守恒(电流连续性)、动量守恒(应力张量连续性)等守恒律的形式一致.

上文把坡印廷矢量拆分为体积内电场能量的时间变化率、磁场能量的时间变化率、功率损耗3部分，在电磁波相关教科书中是常见的.然而，上述关于坡印廷矢量的推导只是从能流角度进行了分析，并没有反映复杂电磁波的不同动量内涵.

2 复杂电磁波的动量密度

事实上，既然坡印廷矢量代表的是电磁场这种特殊物质的能量密度w以速度v的流动，即S=wv(不计能量转化为焦耳热的欧姆损耗).那么这个矢量跟电磁波的动量密度p就紧密联系在一起，即

(6)

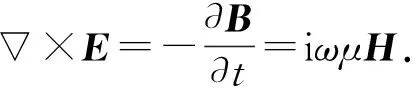
(7)

式中Im{…}为取虚部，j为直角坐标系x、y、z三个分量.与前述坡印廷定理中的散度或通量表达式相对比，式(7)更能体现电磁波的运动特征，与电磁波的传播相位梯度(即波矢)、横向涡旋相位、偏振态及其不均匀分布程度等密切相关，实际上展现了电磁波的动量内涵.

式(7)中的第1项与电磁波的偏振态(自旋)无关[6]，该能流分量正比于轨道动量密度，反映了电磁能量的流动(传输)，是实验可直接观测的量.若考虑电磁波沿+z方向传播的傍轴情况，并把纳布拉算子拆分成横向和纵向两部分，即=T+z.那么，式(7)第1项除以c2，即得轨道动量密度porb的时平值，可表示为

(8)

其中k为单位矢量z方向的传播波矢, 强度I=E*·E.这就把坡印廷矢量对应的轨道动量密度分解成了式(8)所示的横向轨道动量以及纵向轨道动量.前者具有内禀属性，表示电磁波自身内部的涡旋运动；后者则具有外禀属性，表示电磁波外在呈现的整体流动.

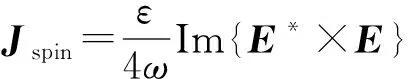
(9)

对于自旋为零的线偏振电磁波、或者对于任意的均匀平面电磁波，式(9)所对应的自旋动量密度均为零.另外，对其取散度，结果恒为零.由坡印廷定理的微分方程式(4)可知：该动量密度不会产生电磁能量的传输(即自旋动量是局域的，对电磁能流在任意闭合面上的通量没有贡献)，可类比传导电流与磁化电流的差异.不过，自旋动量密度非零的不均匀光场(见下文2.3节)，可导致非保守力或力矩，在光驱动纳米马达方面有一定的应用前景[10,11].

对于介质中沿+z方向传播的时谐电磁波，在傍轴条件下电场是横向偏振的，且是z的慢变函数(可忽略z的依赖性)[5].因此，其相量式可表示为E(x,y,z)=E0(x,y)u(x,y)eilθeikz.其中：

1)E0(x,y)为振幅因子(实数)，若强度均匀，则该振幅因子与坐标(x,y)无关;

2)u(x,y)=αx+βy为单位偏振矢量，其中α、β为复数，且满足归一化|α|2+|β|2=1，若u(x,y)与坐标位置(x,y)无关，则表示偏振态均匀分布的电磁波.若单位矢量x、y方向的偏振分量同步(无相差)，则表示线偏振态；反之则为椭圆偏振态;

3) eilθ为涡旋相位因子.其中l为角量子数，θ为横向xy面内的方位角，其正切值对应该位置处坐标y与x的比值，即θ=arctan(y/x).

由于强度因子E0(x,y)、偏振因子u(x,y)、涡旋相位因子eilθ等三者都是x、y坐标的函数(且前两者的具体函数关系还不明确)，直接将复振幅E0(x,y)u(x,y)eilθeikz代入有关公式计算和Jspin的一般形式，会遇到一定的困难. 下文中，我们不妨通过几个典型的例子来阐述前述3种动量密度所对应的物理图像.

2.1 均匀平面电磁波只有纵向轨道动量

对于教材常用的均匀平面电磁波来说，E0、u=αx+βy均为常量(与坐标无关)，且角量子数l=0.此时横截面(xy平面)上的振幅一致、且偏振态均匀分布，其复振幅可表示为E=E0(αx+βy)eikz.则横向轨道动量密度的时平值为

自旋角动量密度为

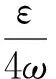
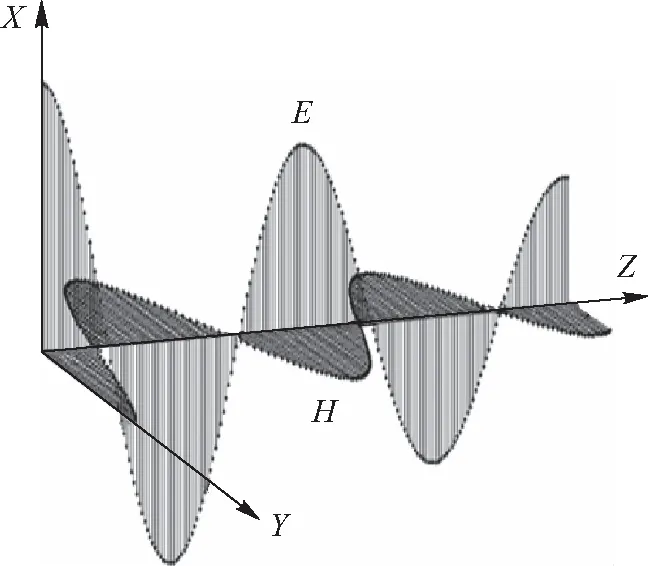
图1 线偏振平面波在损耗介质中传播

2.2 涡旋电磁波具有横向轨道动量

E0β*e-ilθe-ikzT(E0βeilθeikz)}=

其中θ=-sinθx+cosθy为横截面内的角向单位矢量.推导中采用了T的二维极坐标形式上式表明：该复振幅所描述的涡旋电磁波，其横向轨道动量具有涡旋(角向)分布特征.另一方面，由于这里的涡旋电磁波与上文的2.1节相比，仅多了一个涡旋相位因子eilθ，这并不会导致两者的自旋角动量密度有任何差别.因此，此处涡旋电磁波的自旋角动量密度依然为

同样由于Jspin是均匀分布的(E0、α、β都是与坐标无关的常量)，将上式取旋度显然等于零，也即此例涡旋电磁波的横向自旋动量密度恒为零.图2所示是l=-2、沿+z方向傍轴传播时的瞬态螺旋型等相位面(波前).与均匀平面电磁波相比，涡旋电磁波的波矢相对于传播方向z轴有固定的微小倾角，但其方向随方位角θ绕着z轴旋转.图2中用螺旋半径的衰减代表传播过程中的振幅损耗，且螺旋中心轴上存在相位奇点(光强为0).

图2 涡旋光束的螺旋型等相位面

2.3 圆偏态高斯光束的横向自旋动量

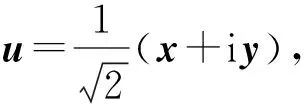
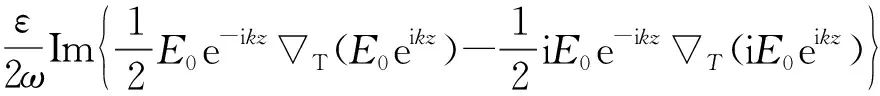
由于振幅因子E0(x,y)是实数，上式不含虚部，结果必然为零，即横向轨道动量密度的时平值为零.该式也表明：强度不均匀不会产生横向轨道动量.另一方面，自旋角动量密度为

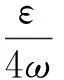
将上式取旋度，可得自旋动量密度的时平值为

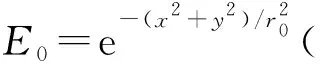
图3 沿+z方向传播、均匀圆偏态的高斯型光场

相比于上述的均匀平面电磁波、涡旋光场、高斯光场，对于一般形式的椭偏态不均匀分布的电磁波(图4，u为复矢量且是坐标x、y的函数)，此时即使电磁波的角量子数l=0，横向轨道动量与横向自旋动量也可以同时存在.不过，考虑到该类光场的动量特征与上述例子大同小异，此处从略.

值得一提的是，还可以从相位(即相量表达式中e指数对应的相角)的角度分析电磁动量[10]：图1中的纵向传播动量是电磁波在空间的传播相位(eikz)产生的；图2中的横向轨道动量是由横向附加的空间涡旋相位(eilθ)产生的；图3的自旋态均匀u=x+iy[可分解为具有恒定相位差(eiπ/2)的两束线偏态相干光场]，但振幅在横截面上不均匀分布.根据本文前述推导与讨论，尽管这种电磁波的横向自旋动量是自旋角动量的幅值梯度分布直接造成的，却也离不开x、y两正交分量的偏振相差；而图4所存在的横向轨道动量和自旋动量，则可以看成是两束正交基偏振态的电磁波之间，存在横向不均匀的相位差所产生的.

图4 不均匀自旋态的矢量光场同时具有纵向传播动量、横向轨道动量和横向自旋动量

(10)

然而，正如电磁波偏振仅以电场分量描述一样，对电磁波动量的描述一般采用式(7)表示.

综上所述，从式(1)所定义的坡印廷矢量出发，可以对复杂电磁波的纵向和横向动量密度、轨道和自旋动量密度进行分类描述.体现了最佳的简洁性和实用性.对于方兴未艾的各类复杂光场，这种基于坡印廷矢量的电磁动量描述方法，在深入了解电磁波的运动特征、以及研究纳米颗粒所受的光力、光力矩等领域，均具有重要的物理意义.