磁共振成像K空间信号的数理模型——以自旋回波序列为例

傅洪波，陈小伟，谢国喜

(广州医科大学 生物医学工程学院，广东 广州 511436)

K空间也称为傅里叶空间，是由带有空间编码信息的磁共振成像(Magnetic Resonance Imaging, MRI)信号填充而成的数据矩阵，每一组MRI图像都有其相应的K空间数据矩阵，它们是傅里叶变换对的关系，对K空间数据进行反傅里叶变换，就能重建出MRI图像.因此K空间是MRI信号空间编码的基础，也是掌握磁共振成像理论的关键环节.

但是，K空间信号表达式的数学物理推导过程鲜见于各类论著及论文中.前期调研发现，现有国内外论著，包括大量教材，直接给出K空间的信号表达式[1-3]，再结合相应图示，以几何化的直观方式讲述K空间是什么和怎样形成，很少有论文(著)对K空间信号表达式的来源进行讨论，而是更多是关注磁共振技术新发展、数值仿真和实际应用[4-6].其中论文[7]虽然能针对成像数据与K空间之间的关系进行数理推导，但推导过程偏于简单，缺乏一些关键细节，比如针对法拉第感应定律的相关推导，仍采用磁化强度矢量，而非定律要求的磁感应强度矢量，对两者关系也未详细说明，导致整个推导过程中的数学物理过程难以理解.另外，我们在互联网上也了解到, 比如，Albert Einstein College of Medicine和Massachusetts Institute of Technology开设相应MRI课程，涉及K空间的部分，也未曾给出一个逻辑完整的介绍，因此根据上述调研的结果，我们认为有必要对此问题展开研究，形成相应的教学支撑.

值得一提的是，Haack E Mark 和 Brown Robert W等人合作的2部著作[8,9]从严密的物理模型和数学处理给出了磁共振三维信号一般表达的推导，但理解该推导过程难度甚高，既要掌握电动力学的相应物理模型又要熟悉矢量微分等数学处理，另外一些关键细节也被省略，没有和序列匹配起来，教与学两方面都殊为不易.但是深刻理解磁共振成像K空间信号表达式既是磁共振成像理论学习的难点和关键，也是相关技术性研发的理论基石，特别是国内MRI这种关键医疗设备仍大量依赖国外产品的背景下，加强我国大学相应的教学，具有深远意义.

针对这一问题，本文在相关文献的基础上，以大学普通物理理论为基础，并从自旋回波序列这一最基本的成像序列出发，结合梯度磁场的空间编码过程、以实例的形式完成K空间信号表达式的数学物理推导，并给出推导过程中的相关细节和依据，试图给学习者提供一个既简单明了，又便于系统地掌握K空间信号模型.

1 磁共振成像与K空间概述

磁共振成像是利用核磁共振原理进行成像的技术，其成像过程简述如下：自旋原子核在静磁场B0的作用下磁化产生宏观磁化强度矢量(以下简称磁化矢量)，磁化矢量在射频场的作用下产生横向分量，横向分量在梯度磁场的作用下实现空间编码，对经过空间编码的磁共振信号进行采集、解调、滤波和放大等处理后，成为填充K空间的数据，对K空间数据进行逆傅里叶变换就可以重建出扫描图像.K空间信号S(kx,ky)与重建图像ρ(x,y)之间是傅里叶变换对的关系：

S(kx,ky)=∬ρ(x,y)e-i2π(kxx+kyy)dxdy

(1)

接下来，我们对式(1)给出相应模型和推导.

2 微元模型的建立

根据量子力学理论[8,9]，处于静磁场中，磁化的氢核产生纵向磁化矢量最大值为

(2)

其中B0为静磁场的磁场强度，ω0为质子的共振频率，γ为磁旋比，k为玻耳兹曼常量，T为热力学温度，ћ为约化普朗克常量，ρ表示该体积内的自旋密度(质子密度)数.

为方便起见，假设成像层面垂直于静磁场，成像层面为xy平面，层厚为Δz，选取该层面内一个体素微元Δzdxdy为研究对象，根据式(2)可构造微元：

Dρ0(x,y)dxdy

(3)

其中，D=γ2ћ2B0/12kT，ρ0(x,y,z)为体素微元的质子体密度，这样ρ0(x,y,z)Δzdxdy表示该体素微元内的质子数，由于断层厚度Δz为常量，可以重新定义ρ0(x,y)为二维像素微元的质子面密度，这样乘以微元面积dxdy后仍等于对应质子数.

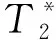
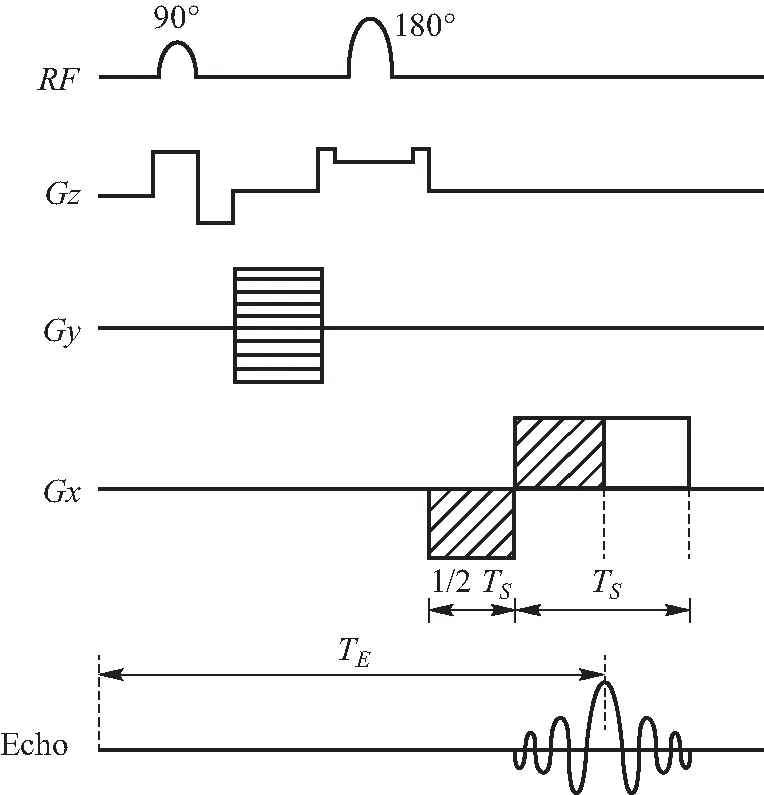
图1 自旋回波序列和空间编码梯度磁场

为处理方便，我们仅讨论TE时刻后采集的数据.结合式(3)和Bloch方程可知Mxy在回波时间TE后的信号大小变化的表达式为

(4)

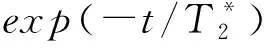
当90°射频脉冲激发后，纵向磁化矢量翻转为横向磁化矢量Mxy，受静磁场和梯度磁场作用，将以角速度ω进动，其大小与Mxy所处位置磁场强度的大小成正比.设某时刻它与x轴正向的夹角为ωt+φ，则断层微元内的横向磁化矢量Mxy在x和y轴的投影大小分别为：

(5)

(6)

式(5)、式(6)中的共有项ωt、φ为：

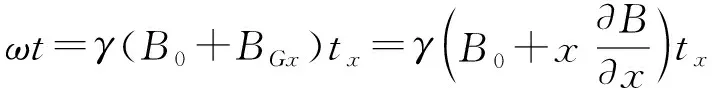
(7)

(8)

其中BGx、BGy分别为频率编码和相位编码的磁场梯度大小，tx为频率编码梯度磁场作用时间，ty为相位编码梯度磁场作用时间.根据图1可知，先进行相位编码再进行频率编码.

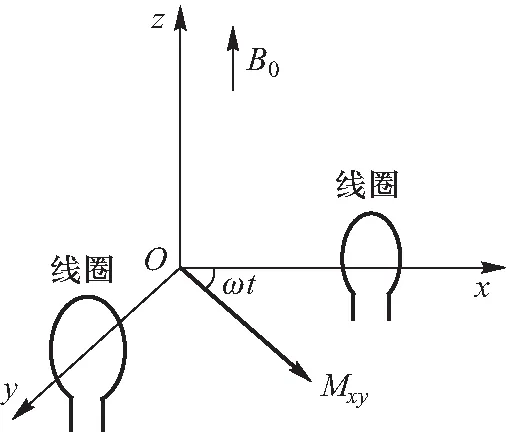
图2 xy平面的横向磁化矢量和正交采集线圈示意图

3 磁共振信号的采集

磁共振成像信号是根据法拉第电磁感应定律进行采集获得的.如图2所示，如果在频率编码梯度时间的同时，在x-y轴分别放置一个有效接收面积为S的闭合线圈，旋转变化的横向磁化矢量Mxy将使得穿过线圈的磁通量发生变换，变化的磁通量将在闭合线圈上产生感应电动势，由此检测到磁共振成像信号，采集得到的数据就是K空间数据.

受论著[8]启发，我们做出以下分析：磁共振成像样品置于静磁场B0中，发生磁化后，产生纵向磁化矢量M0，假设成像组织是由各向同性的顺磁物质构成的，总的磁感应强度B为静磁场强度B0和介质磁化电流产生的附加磁场B′的矢量和[10]：

B=B0+B′

(9)

根据磁化理论可知，真空磁导率为μ0，在静磁场中的磁化矢量为M0的介质，产生的附加磁场B′为

B′=μ0M0

(10)

因此在射频90°脉冲作用下，横向磁化矢量Mxy在静磁场作用下产生的附加磁场最大值为

B′=μ0M0

(11)

该附加磁场在接收线圈处产生相应变化磁通量，即

Φ=B′·S

(12)

其中S为线圈的有效接收面积.

由于接收线圈中总的磁通量是所有微元dxdy的附加磁场B′的累加贡献，结合定积分定义，根据式(5)、式(6)和式(12)，可得图2中x和y轴处的感应线圈中产生的磁通量分别为

Φx(t)=∬Sμ0dMx=

(13)

Φy(t)=∬Sμ0dMy=

(14)

其中S为线圈总的有效接收面积，为简单计，这里设两组线圈的S相等.

根据法拉第电磁感应定律，感应电动势为

(15)

将式(13)、式(14)对时间求导可得

(16)

(17)

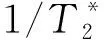
εx(t)=-∬μ0Sω0C(x,y)sin(ωt+φ)dxdy

(18)

εy(t)=∬μ0Sω0C(x,y)cos(ωt+φ)dxdy

(19)

4 K空间的积分表达

K空间是复空间，K空间数据是由x、y方向测得的信号强度分别作为复数信号的实部和虚部，即

ε(t)=εy+iεx

(20)

根据欧拉公式得

ε(t)=μ0ω0SC(x,y)e-i(ωt+φ)dxdy

(21)

成像断层的所有微元集成后的磁共振信号为

ε(t)=∬μ0ω0SC(x,y)e-i(ωt+φ)dxdy

(22)

实际应用中在得到式(22)之前，还需借助信号“解调”技术消除上面式(18)、式(19)感应信号中类似载波的高频成分ω0.解调是用频率接近或等于ω0的正弦或余弦函数与信号相乘.比如用参考信号sin(ω0t+ω0ty)乘以式(21)，借助三角恒等式，可得解调后信号为

sig=sin(ω0t+ω0ty)sin(ωt+φ)=

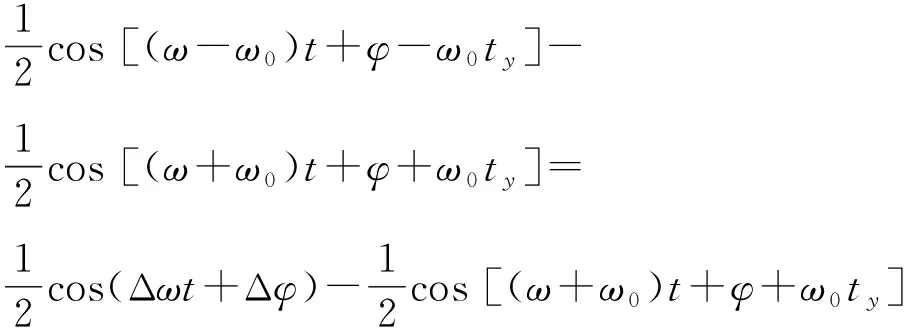
(23)

对于式(23)中对应高频信号部分，利用低通滤波去掉，只剩下Δω对应的低频部分，对于虚部通道也做类似处理，最终式(21)变为

ε(t)=∬μ0ω0C(x,y)e-i(Δωt+Δφ)dxdy

(24)

其中

(25)

(26)

需要说明的是对于式(25)而言，当施加线性梯度磁场时(设中心处梯度为零)，解调后信号可表达为

(27)

式(27)中梯度磁场∂B/∂x在信号采集时间Ts内只是空间x值的函数，其大小不随时间变化，这是使用线性梯度场且不考虑梯度切换情况的特例.如图1所示，该梯度沿时间轴依时序施加，但对于某一空间位置上的梯度磁场大小不变.其实，类似处理相位梯度磁场带来的相位变化，我们可认为Δωt就是频率编码通过时间t带来的累积相位，此时表达式(27)重写为

(28)

积分形式的式(28)成为教科书中常见的表达，这种积分表达式在更复杂的磁场梯度的时变技术中还有其他应用和解释.必须指出的是，式(28)的积分表达的时间区间[0,t]，本推导中以TE时刻为计时零点，即为[0,Ts/2].至于y方向的相位编码的整个积分时间也记为[0,t]，则为相位编码梯度磁场的独立的实施加载时间.

借此机会，我们补充说明下，借助K空间的对称性，本推导涉及的采集信号实际只填充一半K空间，实际上，由于K空间的共轭对称性，另一半K空间数据也可以用本文的方法进行讨论.而填充一半K空间，类似于快速成像中的“半扫描技术”(通常意义是利用相位编码带来的矩阵行的对称性)，也称作部分傅里叶(Phase Partial Fourier).我们采用该技术概念的目的是为了模型的简化和表达的一致性，比如回波信号按exp(-t/T2)规律衰减，没有涉及TE重聚相前采集的另一半信号，以此避免带来的描述和解释的复杂性，而按照图2，实际采集的信号是完整的.

接下来，利用式(25)、式(26)，给出K空间的“k”的定义表达式：

(29)

(30)

再令ρ(x,y)=μ0ω0SC(x,y)，此时ρ(x,y)构成学者俎栋林、高家红在文献[1]提出的“广义自旋密度”.最终式(24)可重新表达为

ε=S(kx,ky)=∬ρ(x,y)e-i2π(kxx+kyy)dxdy

式(1)的再次呈现，也意味着我们完成了对K空间信号的定量公式的推导.

5 讨论与总结

正如前文所述，K空间虽然是磁共振成像的重点内容，但其理解殊为不易.以式(1)而言，一旦无法清楚其来龙去脉，可能产生一些误解，比如简单理解ρ(x,y)就是自旋密度，甚至没有意识到K空间是复数空间.至于K空间和诸多前期概念(比如加权成像)之间的逻辑关系，在缺乏相应数理逻辑背景时，真正透彻地理解磁共振成像更是无从谈起.因此，本文通过一个斧凿和裁剪过的数模模型给出了相应的逻辑推导的前提和过程，给K空间信号一个系统的、定量的、简单的解释.

本研究的系统性在于有效地串联了一系列前置概念，并把采集和信号处理相关环节也纳入其中，形成完整、紧密的逻辑链，同时也加深了MRI加权图像与K空间信号的联系与理解.其定量化体现为各逻辑环节的公式化，最终自然地过渡到K空间信号表达式即式(1).简单性在于本论文在推导过程中合理降低了相应物理模型和数学处理的复杂度，给出一个实例化、具体化、解释性强的K空间信号模型.