格林互易定理在静电学和检验数学恒等式中的应用
2022-02-18宋雨霏梁兆新
宋雨霏,梁兆新
( 浙江师范大学 物理学系,浙江 金华 321004)

格林互易定理在电动力学中有巨大应用价值.相较于传统的镜像法和本征函数展开法等方法,格林互易定理的特点是只需要着眼于物理系统两种静电状态的电势和电荷,通过巧妙设计电荷和电势分布消除不必要的未知量从而获得结果.其解题逻辑清晰易懂,步骤简便,对于一部分静电学的问题,有明显的解题优势.例如,丁健和李奎春[1]对格林互易定理在均匀带电圆环的静电势分布的应用; 王军杰和金彪[2]对格林互易定理在中学竞赛中的应用也进行了详细的介绍.但是都没有将静电学中几种常见的方法与格林互易定理进行对比与讨论,也缺少格林互易定理在导体球壳导体球上的应用.
本文内容主要分为3个方面:1)对格林互易定理进行了严格数学证明,并强调了其成立所需满足的物理条件;2)选取静电学中最典型的几类例题分别用镜像法、本征展开法以及格林互易法进行求解分析,通过比较展示了格林互易定理在求解某些静电学问题中的优势.另外,通过列表总结了镜像法、本征展开法和格林互易定理法在求解静电学问题时各自的优缺点;3)讨论格林互易定理在实际物理问题中的应用,提出检验拉马努金无限求和公式和其他几个数学恒等式的实验方案,并形成一套验证数学恒等式的物理方法.
1 格林互易定理证明
格林互易定理严格数学证明虽然在一些教科书中给出,但是在国内大学广泛使用的郭硕鸿著《电动力学》中没有被提及.为了保持本文理论框架的完整性,下面我们将给出格林互易定理的严格证明.
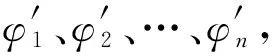
证明:给定任何闭合区域S,在此中选择2个连续可微的函数Ψ、Φ,由高斯定理可得
(1)
互换Ψ、Φ两个函数位置,再应用高斯定理可得
(2)
将式(2)与式(1)相减得
(3)

(4)
化简可得
(5)
(6)
积分后可得格林互易定理:
(7)
式(7)的适用条件[3]:无限大空间中有限带电体;静电静磁导体情况适用.
2 格林互易定理在静电学中应用[4]
静电场就是相对观察者静止的电场,静电场是研究电场的基础,为后续研究电磁波的传播奠定基础.处理静电场问题的方法有本征展开法(分离变量法)、镜像法、格林函数法等.这些方法的核心是将物理问题转化为数学物理方程进行求解,计算复杂,在某些问题中操作困难.本文将格林互易定理与这几种方法进行比较.
2.1 点电荷与接地导体球
接地导体球和点电荷问题是静电学中最常见的问题,展现了最基本的导体电荷与电势的关系.现给出一例题,如图1所示,题目如下:在真空中将半径为R的金属球接地,在与球心O相距为d(d>R)处放置一个电荷量为q的点电荷,不计接地导线上电荷的影响,求金属球表面上感应的电荷量.
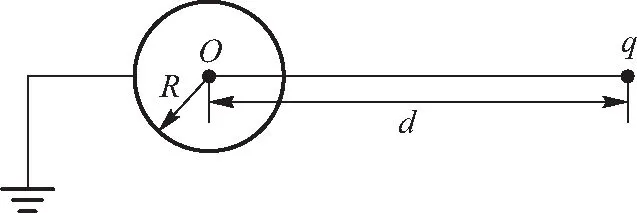
图1 接地导体球与点电荷
该例题用镜像法和格林互易定理都可以求解,但是前者要比后者繁杂得多.本文将用2种方法求解并进行对比.因为镜像法在郭硕鸿著《电动力学》第3版第54页有详细过程[5],在这简略地介绍.
2.1.1 镜像法
已知球外的电势满足如下泊松方程:
(8)
由于金属球静电平衡则在球内部E为0,所以内部的电势不做考虑.容易得到边界条件:
φ|r=R=0,φ|r→∞=0
(9)
对于φ外来说球内即为虚拟空间,在球内设虚拟电荷不影响外部.又因为球的旋转对称性,电荷只能在极轴上,即水平轴.现令球内虚拟电荷为-q′,其位置距离球心为b,将球心与q的距离用d来表示.现取球外任意一点o′,o′距q的距离为rd,距-q′的距离为rb,与球心的距离为r,则其电势为
(10)
令r与水平轴的夹角为θ,可得
(11)
由于对于任意的夹角都成立,则与角度无关,可得
-2Rbq2=-2Rdq′2,
(R2+b2)q2=(R2+d2)q′2
(12)
之后就可求得q′和b同时也能求得球表面电荷,积分后获得球表面的感应电荷.该方法过程复杂,计算繁琐,同时需要一定的空间想象能力.
2.1.2 格林互易定理法[6]
格林互易定理的核心是通过设置不同充电模式,让式(7)与题无关的量交叉相乘为零,从而求得需要的量.以题意为第一种充电模式,在这种充电模式下导体球接地,以地为电势零点,则此时φ球=0,而φq未知.令qR为所求电荷量,也就是球表面的电荷,则第1种充电模式为
{qR,q}, {0,φq}
(13)
现在让导体球不接地并且给予电荷量q′,令点电荷为零,则第2种充电模式为
(14)
根据格林互易定理,式(13)和(14)的2种充电模式交叉相乘可得
(15)
最后很容易得到导体球表面感应电荷量为
(16)
两种方法计算结果完全相同,但格林互易法不管从计算难度,方法步骤还是物理思想上都要比镜像法简单得多.
将这道题进行扩展,再加几个点电荷或者导体球.如图2所示,在原来的基础上增加一个距离圆心r,电荷量为Q的点电荷.如果用镜像法,两个以上的点电荷无法很好的镜像,很难计算.但是用格林互易定理,就会很简单.
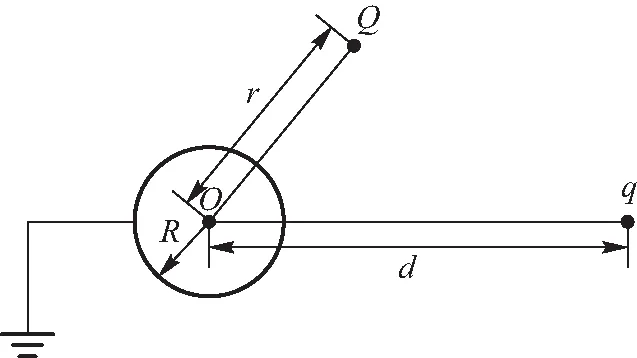
图2 接地导体球与两个点电荷
根据上述格林互易定理解法得第1种充电模式:
{qR,q,Q}, {0,φq,φQ}
(17)
令导体球不接地并给予电荷量q′,其余点电荷零,则第2种充电模式为
(18)
交叉相乘可得
(19)
用格林互易定理解决该类问题方便快捷,物理思维简单易懂.
2.2 接地导体球壳与导体球
当问题变复杂,把2.1题目中的点电荷变为导体球壳,此时镜像法就无法使用,但格林互易定理还能应用,轻松解决该问题.
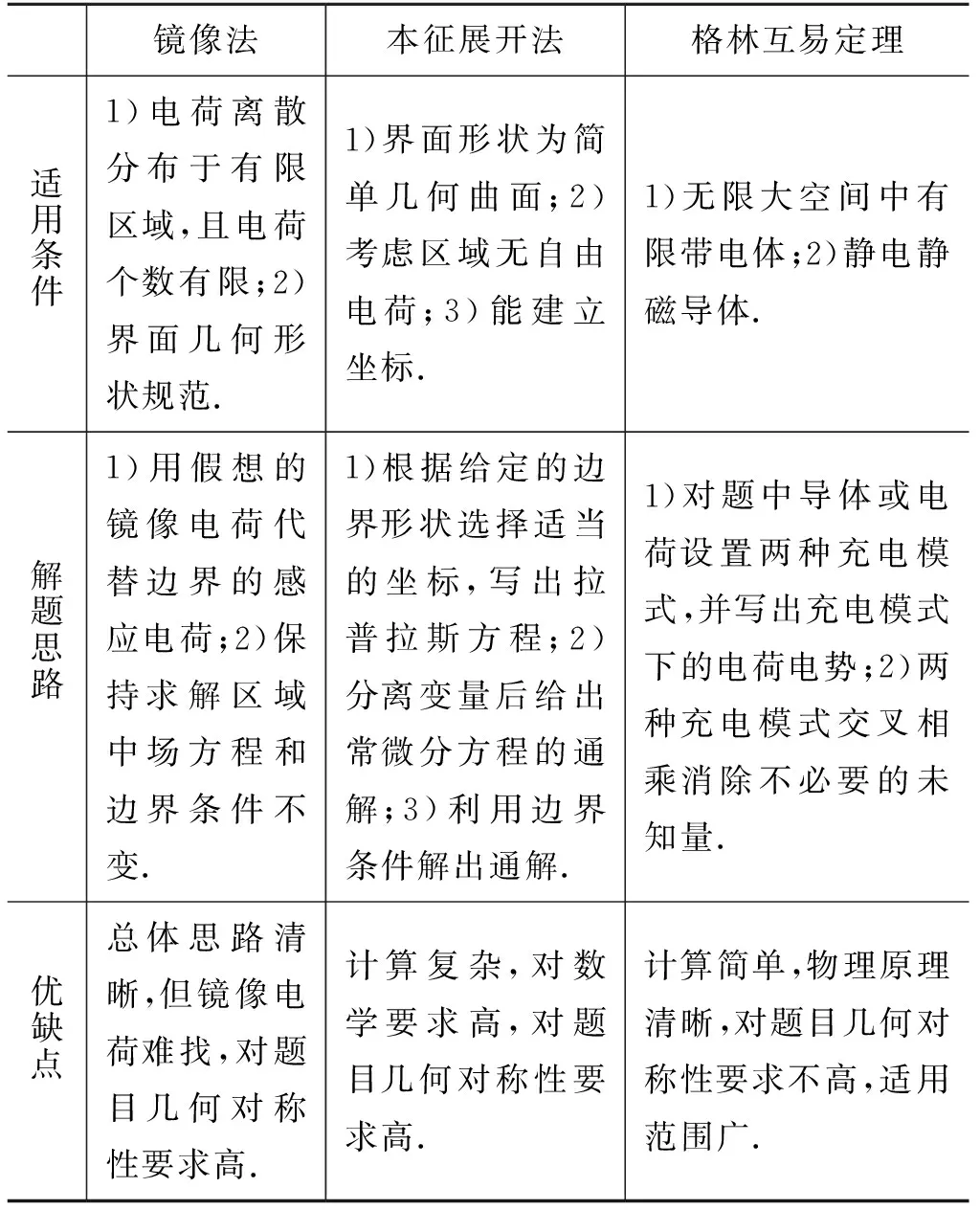
如图3所示,内外径分别为R2、R3导体球壳,带电荷量为Q,同心地包围着一个半径为R1的接地导体球,R1 图3 导体球壳与接地导体球 该题虽然不能用镜像法,但可以使用本征函数展开法,过程繁琐复杂.本文将用本征函数展开法和格林互易定理求解并进行对比. 选图3所示导体部分之外的介质(真空)部分为研究体系,由于球对称,解不依赖于角度,则电势的通解为 (20) 设不同区间的电势为 (21) 由题意知边界条件: φ2|r=R1=0, φ1|r→∞=0, φ2|r=R2=φ1|r=R3 (22) 除此之外还有关于电荷导出的边界条件: (23) 化简可得 (24) 接下来将所设的电势代入边界条件并联立求出未知的量即a、b、c、d,可解出φ1和φ2.用本征函数展开法将一个物理问题变成了一个数学问题,减少了题目包含的物理思想.并且本征函数展开法需要知道通解的表达式,边界条件计算复杂,不容易求解. 2.2.2 格林互易定理法 假设中心球带电荷量为q,把导体球壳看成一个整体,则第1种充电模式: {Q,q}, {φ,0} (25) 对于第2种充电模式,假设中心导体球不接地,并令其所带电荷量为q′,φ1为球壳上的电势,φ2为中心导体球上的电势.此时球壳上的电荷量为0,则 {0,q′}, {φ1,φ2} (26) 现计算φ1和φ2,有 (27) 由于球壳上的电荷为零,则壳内侧的电荷和壳外侧的电荷相加为零,可得 (28) 由于静电平衡则在球壳内表面感应出了-q′的电荷量,在球壳外表面感应出了q′的电荷量,则利用格林互易定理交叉相乘可快速求得 (29) 感应电荷求出,则代回电势表达式可求出电势.可见格林互易定理在解这类题目时也是非常方便的. 通过前面2个例子,可以知道格林互易定理可以使部分题目解题过程得到很大的简化,但是用其他方法也可以做.接下来的例子无法用静电学其他常用的方法进行求解,但从格林互易定理入手可以大大简化题目难度,快速求解. 如图4所示,有无穷块平行放置的正方形大导体板,每块边长均为L,相邻两板彼此相对的两个表面的问距均为d,d≪L.将这些导体板从左至右顺次编号为1,2,…,n,….开始每板上都带有净电荷,已知第1块板上的净电荷量为q1(设q1>0),第n块板上的净电荷量qn=nq1,现将第1块和第n块导体板接地.忽略边缘效应,1)忽略n块极板之后的极板,第n块导体板上流入大地的电荷量Δqn为q1的多少倍?2)假设只有n块极板,上述两板接地后n块板中哪块板上的电势最高? 图4 无穷平行板电容器 现在用格林互易定理进行求解.由题意可知,当第1块和第n块导体板接地后,这两块板电荷量发生改变,所有极板的电势也发生了改变,但n极板之后的极板则可设第1~n块极板的总电荷量和电势分别为: (Q1,2q1,3q1,…,(n-1)q1,Qn), (0,U2,U3,…,Un-1,0) (30) 对于第1问:改变导体板上的电荷量,使第一块板子带电荷量为-Q,最后一块板子带电荷量为Q,中间板子都不带电.并且第一块板子接地,最后一块板子不接地.令C为相邻两板间的电容则板子的电荷量和电势分别为: (-Q,0,0,…,0,Q), (31) 利用格林互易定理可得 (32) 计算可得 (33) 最后即可解出答案为 (34) (0,0,…,-q,q,0,…,0), (35) 将其与题目所得条件进行格林互易,则得到 (36) 与式(33)联立可得 (37) 要将3k(k+1)与n(n+7)进行比较,当这两者相接近时,取两者差值的绝对值较小时的k. 通过2.1—2.3节,可以看出镜像法、本征展开法与格林互易定理在求解静电学问题时各有千秋.考虑到在郭硕鸿著《电动力学》这本国内大学物理系广泛使用的教材中没有介绍用格林互易定理法,在表1中详细从适用条件、解题思路和优缺点3方面分析了3种解题方法的优劣. 表1 镜像法、本征展开法与格林互易定理比较 拉马努金是印度历史上最著名的数学家之一,提出了很多以其名字命名的数学恒等式.其中最著名的公式之一为 (38) 式(38)可以通过解析延拓黎曼ζ函数的定义域(ζ函数正则化)而得到.式(38)虽然数学非常合乎逻辑,但却给出有悖常理的结果,违反了数学直觉,但式(38)在物理上有巨大应用.例如,在玻色子弦理论中[7],式(38)被用来计算无限次量子谐振的总能量.这个事实也被用来说明弦理论在26维以外的维度上是不一致的.式(38)也被用来计算一维标量场的卡西米尔力[8],其中式(38)中的负号反映了卡西米尔力是吸引力.式(38)惊人的结果也可在量子力学其它领域以及未来更多领域得到应用. 考虑式(38)的有悖常理的反直觉性,本文提出一个理想实验来检验式(38).下面本文将2.3节的例题改进成为一个理想实验,通过先验(priori)的逻辑方式,基于格林互易定理来对式(38)进行可视化实验验证.下面设计如下理想实验: 1) 如同2.3节中的图4,将首尾两个平行板接地,中间等间距插入无穷多个平行板,并且首尾极板之间的距离有限,极板与极板间距远小于平行板的长度; 3) 格林互易定理仍然适用于改进的理想实验.仿照2.3节第1个问题的做法得到 (39) 其中式(39)右边括号中涉及无穷项求和的问题. 上述验证拉马努金公式(38)的实验方案提供了检验一类代数求和公式的物理方法.该方法的核心要点为:上述步骤2中所要求的第K块板上的净电量与q1之间的关系要尽量简单并实验可行.据此,可以根据格林互易定理检验如下代数求和公式. (40) (41) (42) 总之,本文希望通过构造基于格林互易定理的理想物理实验去检验一些数学恒等式,使得抽象的数学公式变得物理可视化,为物理和数学有机结合提供新思路.另外,我们相信可以将此方法扩展到检验其他一些具有物理重要性的数学公式中去. 虽然很多教课书中给出了格林互易定理证明,但为了保持本文理论框架的完整和自洽性,首先,本文对格林互易定理进行了严格的数学证明并说明其适用条件;其次,通过几个对称性的静电学实例,比较了镜像法、本征展开法和格林互易定理法在求解静电学问题时的优劣.可知镜像法只适用于所考虑区域内只有一个或几个自由电荷并且区域边界是导体或者介质界面的情形;本征展开法只适用于所考虑区域内没有自由电荷分布的并且界面形状必须是简单的几何曲面的情形;而格林互易定理除了适用于前两种情形还可以求解一些电容或带电圆环等问题,充分体现了其在处理静电问题上的优势;最后,本文基于格林互易定理以拉马努金无限求和公式和其他几个常见的数学恒等式为例,提出了一种利用理想物理实验检验一类代数求和公式的方法,希望数学和物理有机结合,相互促进发展.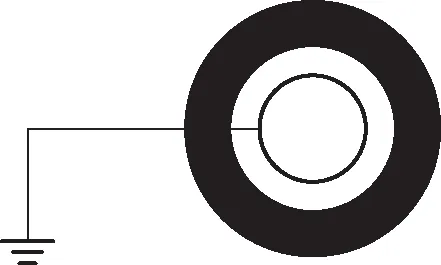
2.2.1 本征函数展开法

2.3 无穷层平行板电容器

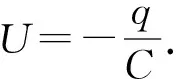
2.4 镜像法、本征展开法与格林互易定理比较
3 检验拉马努金无限求和公式的理想实验
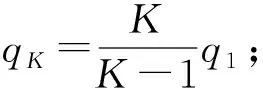
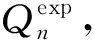
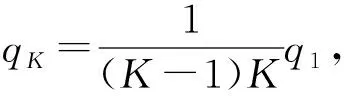
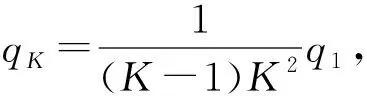
4 总结
