孔管型支承结构的弹性跟随行为及优化研究

2022-02-17曾晓佳莫亚飞高付海赵守智

压力容器 2022年11期

李智,曾晓佳,莫亚飞,高付海,赵守智

(1.中国原子能科学研究院核工程设计研究所，北京 102413;2.国防科工局核技术支持中心，北京 100070)

0 引言

快堆内孔管型支承结构主要用来为上部设备(例如：中间热交换器[1-2]和独立热交换器[3]等)提供支承；同时热钠通过结构密集开孔段(以下均称孔管段)进入内部换热设备进行换热使结构产生冷冲击和轴向温度梯度，因此在设计时需针对孔管型支撑结构在长时交变高温环境下的强度、变形和寿命进行评价。然而由于密集开孔导致孔管段局部刚度不连续，存在弹性跟随现象，显著放大了孔管段因轴向温度梯度产生的热应力、残余塑性应力和塑性应变，所以在结构的设计和优化时需针对其弹性跟随效应进行重点分析。

弹性跟随现象，即当不同刚度或者强度的结构零部件连在一起且柔性部分处于高应力状态时，可能产生异常大的应变集中现象。1955年，ROBINSON[4]解释螺栓连接因为高温蠕变产生的松弛行为时提出了弹性跟随效应。ISOBE等[5]基于弹性跟随的试验方法，研究了快中子堆316不锈钢的裂纹扩展和蠕变-疲劳寿命预测，提出当结构疲劳寿命很长时，基于延性耗竭法推测蠕变寿命较时间分数法更加保守。AINSWORTH等[6]提出了在非弹性分析中基于弹性跟随的存在与否进行一次应力和二次应力的组合方法。SMITH等[7-8]基于弹性跟随试验研究了316不锈钢结构在内部残余应力和外载荷共同作用下的蠕变松弛和裂纹扩展特性。KASAHARA等[9]建立弹性跟随模型评估日本文殊快堆中局部刚度不连续结构的高温强度和蠕变寿命，并针对文殊堆局部过渡区域建立弹性跟随模型来提高局部区蠕变-疲劳损伤计算的准确度。BOYLE[10]阐述了针对稳态蠕变速率与结构应力范围有关系的高温结构应用，以及目前弹性跟随系数方法描述弹性跟随现象存在误差的原因。ROCHE[11]提出管系结构中强度弱的一侧对于另一侧相当于一个弹簧结构，在高温下会发生蠕变断裂。秦叔经[12]以端部固支两相连管系为例，指出当相连接的两个结构之间强度相差悬殊、不考虑结构塑性和蠕变特性时，应力分类方法得到的结果与实际结果存在较大的偏差，该偏差将使得分析结果偏于冒进。张向兵等[13]基于弹性跟随法的概念，以标准椭圆封头带中心接管结构为例，详细分析了采用分部法和整体法进行管系附加载荷处理的结果差异，并对管系和容器连接的工程实例进行了分析研究，发现弹性跟随效应使得塑性分析下管系和容器连接处存在局部应变集中，且应变比弹性分析下要大。

本研究则基于弹性跟随相关理论，分析弹性跟随对孔管型支承结构热应力、残余塑性应力和塑性应变的放大现象，并以降低应力和应变为目标，提出孔管型支承结构优化的方向。

1 孔管型支承结构的弹性跟随特征分析

典型孔管型支承结构如图1所示。结构整体分为上中下三部分，中间密集开孔段为孔管段部分，上下两端为圆柱实体。结构孔管段和上下两端交界处局部刚度不连续的特征使结构存在弹性跟随效应。

图1 孔管型支承结构Fig.1 Hole tube type support structure

本文采用两端固支多孔平板模型对弹性跟随现象的产生及其对结构强度和刚度的影响进行了原理解析。图2将多孔平板简化为刚度不同的双杆模型(图中G表示刚性段，R表示柔性段)。假设无孔段刚度为KG，带孔段刚度为KR，双杆模型中G杆和R杆弹性模量相同，G杆的横截面面积大于R杆。

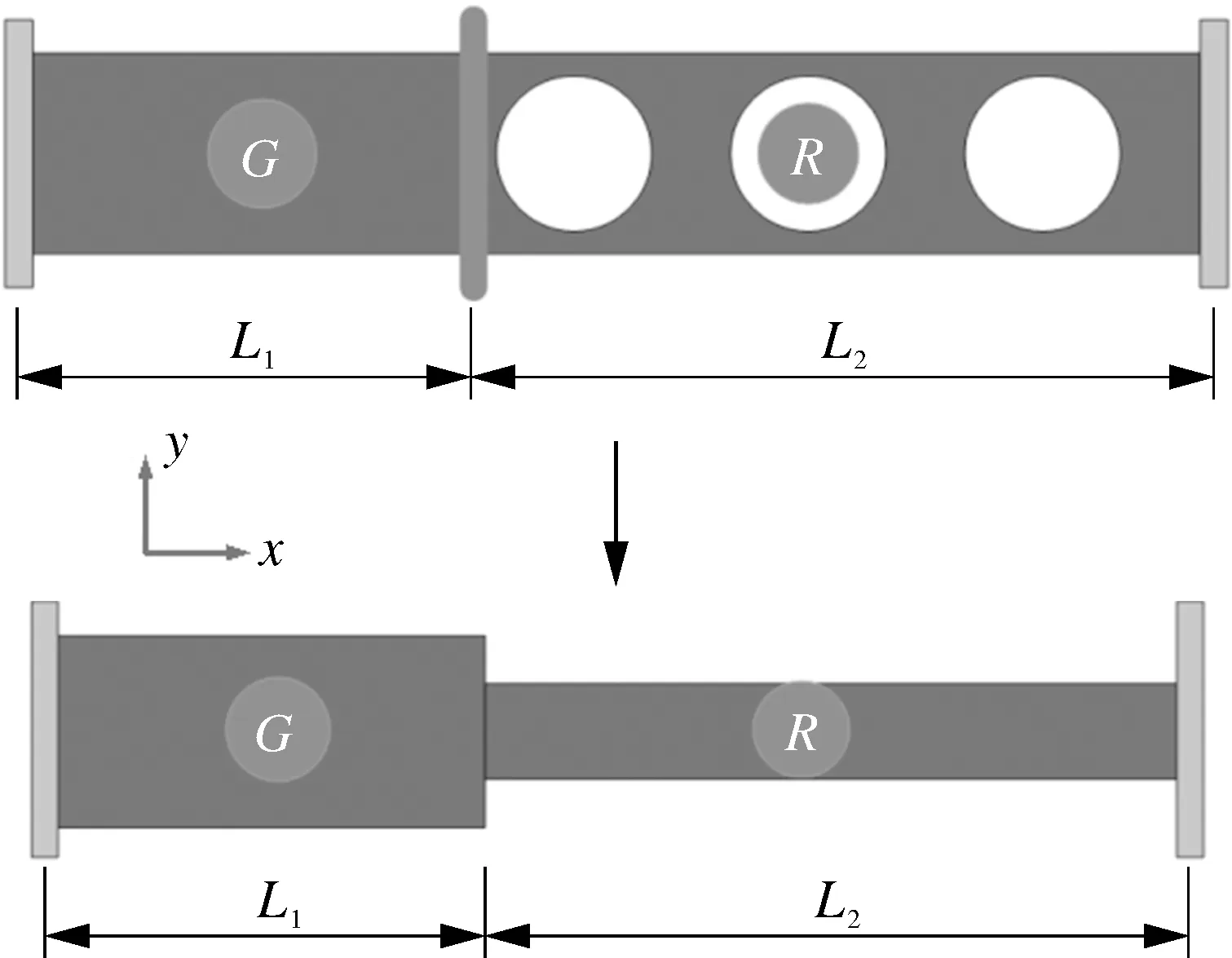
图2 双杆模型Fig.2 Two-bar model

给定温升ΔT，结构两端固支导致结构产生的x正方向热变形无法释放，从而使得G杆和R杆均受压，其位移协调条件和力平衡方程如下：

ΔG+ΔR=αΔT(L1+L2)

(1)

FG=KGΔG=FR

(2)

式中,ΔG为G杆压缩量;ΔR为R杆压缩量;α为热膨胀系数。

力-位移曲线图如图3所示，图中左侧为G杆力-位移关系，右侧为R杆力-位移关系。实线段：G杆和R杆二者均为弹性情况；虚线段：G杆处于弹性状态，柔性段进入屈服状态。对比实线段和虚线段可知，进行塑性分析时承载能力弱的R杆进入屈服且塑性应变增加，产生局部应变集中，同时可能增加降温时的残余应力。

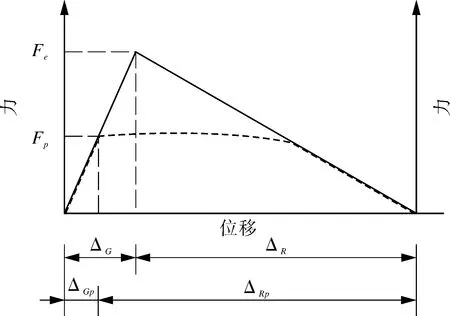
图3 力-位移曲线Fig.3 Force-displacement curve

假设G杆和R杆均在弹性状态，分析G杆刚度和长度对结构应力的影响。位移边界条件和平衡方程如下：

εGL1+εRL2=αΔT(L1+L2)

(3)

EAGεG=EARεR

(4)

(5)

式中,εG，εR为G杆和R杆受压弹性应变；E为弹性模量；AG,AR为G杆和R杆的面积。

联立式(3)～(5)可得R杆弹性应变如下：

(6)

当KG>>KR时，针对R杆弹性应变分两种情况进行讨论：

(1)G杆长度L1≠0，此时εR=αΔT(L1/L2+1)；

(2)G杆长度L1=0，此时εR=αΔT。

上述第二种情况即整体结构刚度相同时R杆应变。由于L1/L2+1>1，因此结构中G杆会引起R杆弹性应力的增加，且随G杆长度的增加而增加，如图4所示。当G杆长度和R杆长度一致时，结构弹性应力为无G杆时的2倍，即考虑塑性时，G杆的存在将导致R杆提前进入屈服。

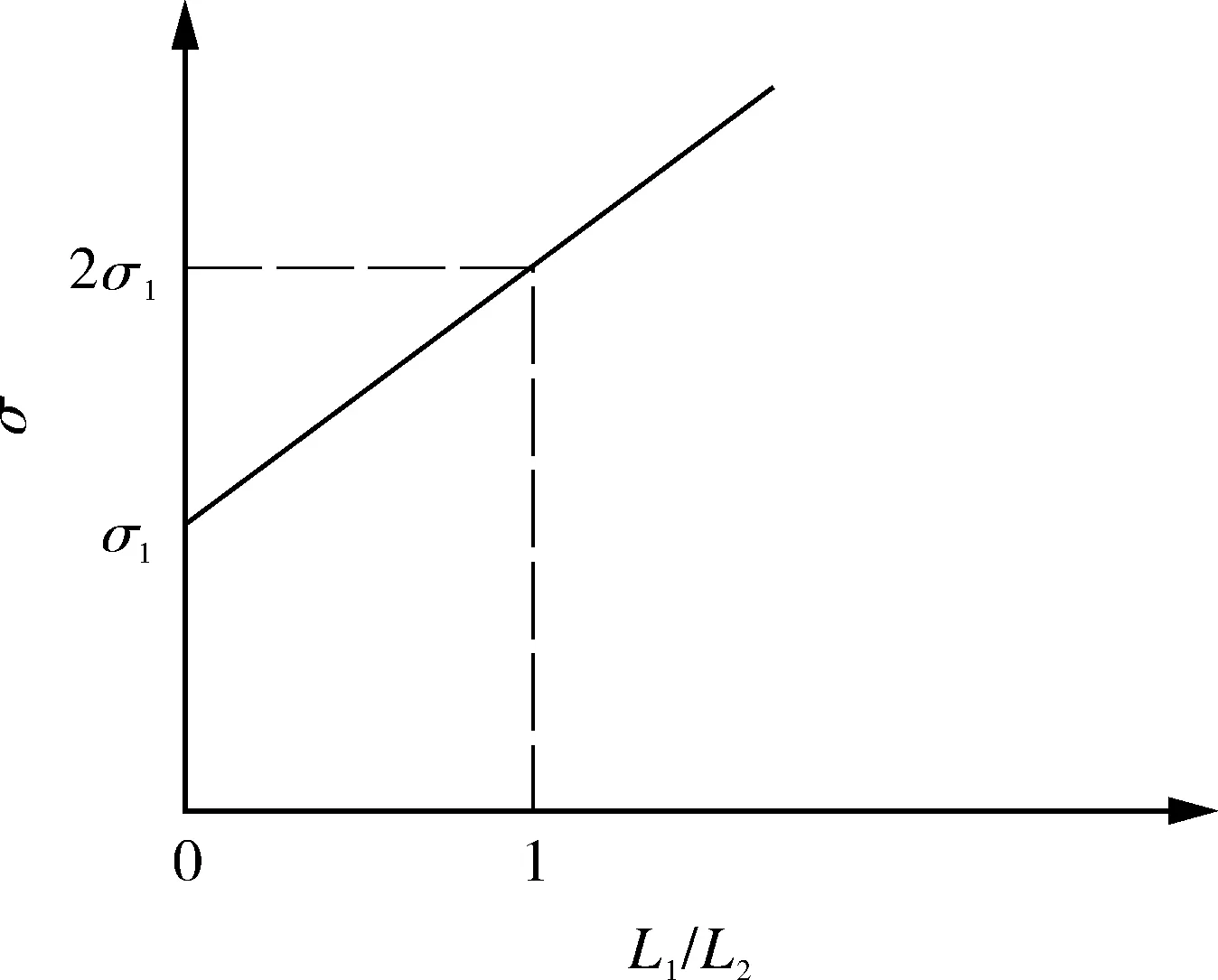
图4 结构弹性应力与G杆和R杆长度比的关系示意Fig.4 Schematic diagram of relationship between structural elastic stress and length ratio of G and R rods

经过以上分析可知，两杆连接刚度不同引起的弹性跟随现象导致柔性段应力增加，柔性段提前进入屈服；与刚度相同的双杆模型相比，R杆的塑性应变增大，产生局部应变集中现象，同时导致降温时残余应力增加。将以上结论推至快堆孔管型支承结构可知，在长时交变高温环境下，结构局部刚度不连续的特征会放大孔管段因冷冲击和轴向温度梯度产生的热弹性应力、残余塑性应力和塑性应变。

2 孔管型支承结构的热弹塑性非线性数值分析

孔管型支承结构如图1所示，结构外径为2 510 mm，厚度35 mm，总长2 148 mm，单一阵列分布15个直径为50 mm的圆孔。本节采用有限元方法对轴向温升及温差作用下的孔管型支承结构进行热弹塑性分析，通过对比弹性和非弹性分析结果，阐述弹性跟随效应在结构中的具体体现；通过分析不同应变随时间的变化曲线，阐述残余应力产生的原因。

2.1 载荷和边界条件设置

本文载荷只考虑轴向温度梯度引起的热应力，因此图1所示结构和载荷均为轴对称。如图5所示，取单一阵列圆孔，结构两侧设置为轴对称边界条件，底边约束沿轴向位移；有限元模型单元为S8R，单元数11 946，节点数38 042。结构温度场如图6所示，孔管段经受冷冲击从而产生大的轴向温度梯度。随高度变化的温度导致结构不同高度热膨胀不同，同时热变形释放受环向轴对称边界条件约束，因此结构中产生较大热应力。

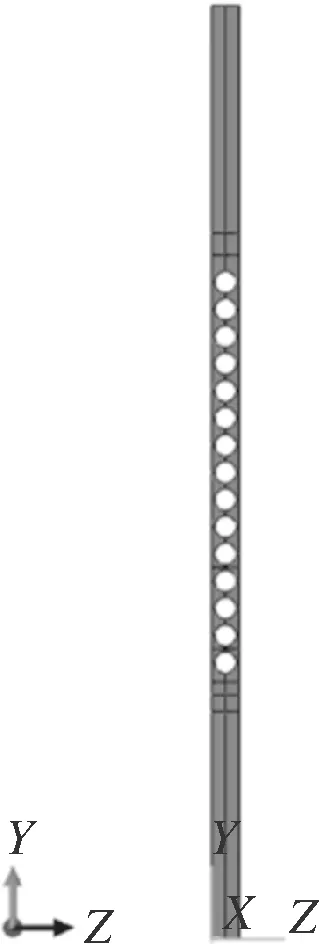
图5 单一周向阵列模型Fig.5 Single circumferential array model

图6 温度场分布Fig.6 Temperature field distribution

结构孔管段在运行中由轴向温度梯度大和结构底端承受冷冲击产生的热应力导致孔管段进入屈服状态。孔管段材料为316不锈钢，屈服强度参考ASME B&PVC-Ⅲ-5中的材料数据，弹性模量和泊松比见ASME B&PVC-Ⅱ-Part D。文中采用von Mises屈服函数，其公式如下：

(7)

(8)

(9)

式中,σy为屈服强度；σ,σ′为应力张量和偏张量;运算符“:”代表张量运算中的并联式双点击运算，即：A:B=AijBij。

f<0时，结构为弹性状态；f=0时，结构进入塑性。

各向同性强化单轴应力-应变关系见图7，图中σ1为初始屈服强度，随拉伸应力的增加强化至σ2，随后经反向压缩至应力σ≥σ3(σ3=σ2) 时，结构反向屈服。结构反向屈服可能导致当前等效塑性应变的降低(见图7)，当反向应力σ=σ4时，反向卸载之后当前等效塑性应变ε4<ε2。

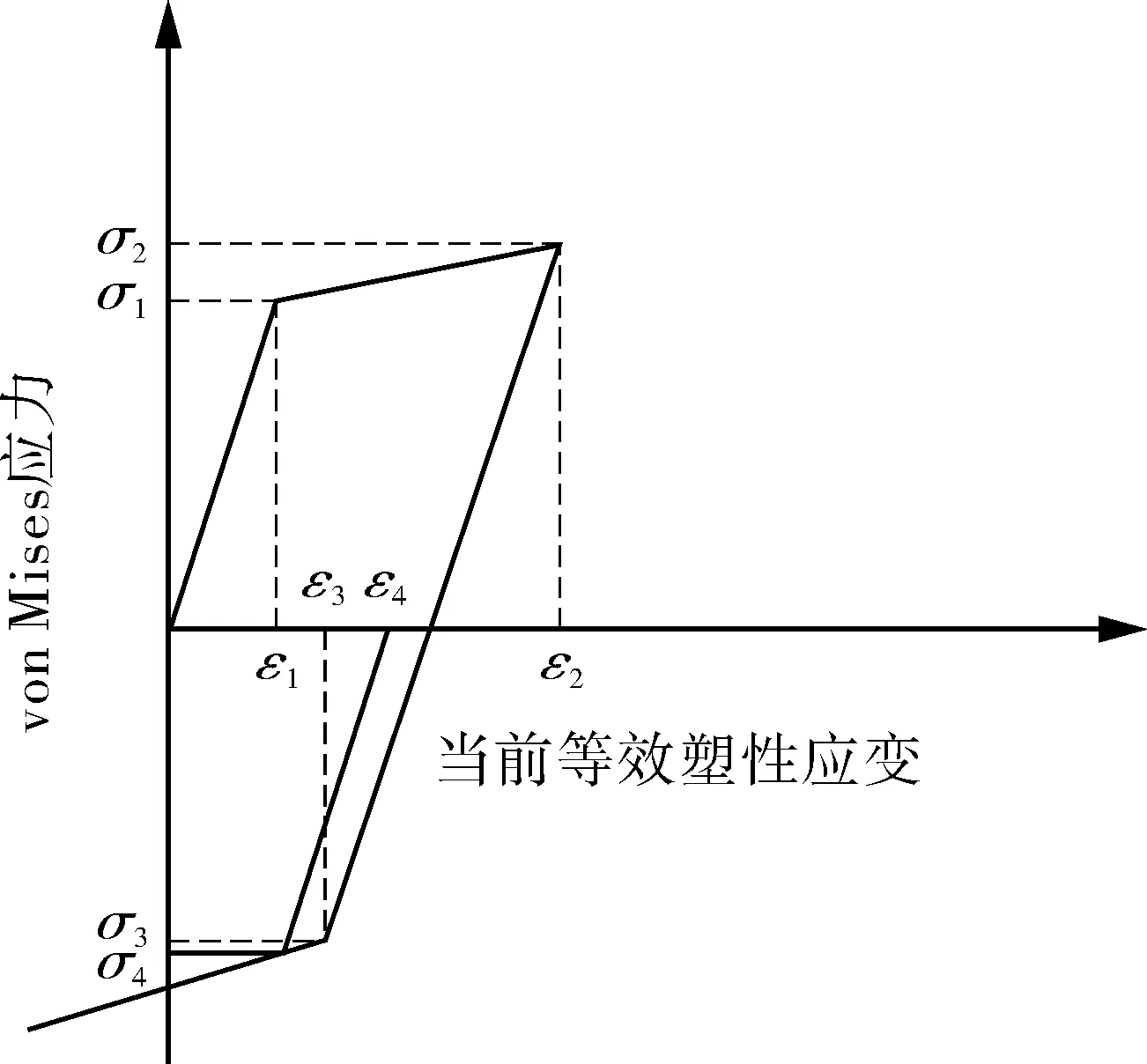
图7 应力-应变示意Fig.7 Stress-strain diagram

2.2 弹性跟随效应验证

基于Abaqus进行载荷分析步设置。弹性分析：设置一个分析步，结构初始温度为250 ℃，结束温度场分布见图6。塑性分析：第一个分析步结构整体温度为250 ℃，第二个分析步温度场分布见图6，第三个分析步结构整体温度为250 ℃，即升温-温度平衡-降温三个阶段。上述单个分析步时长为1。图8示出结构塑性分析和弹性分析的应力结果。

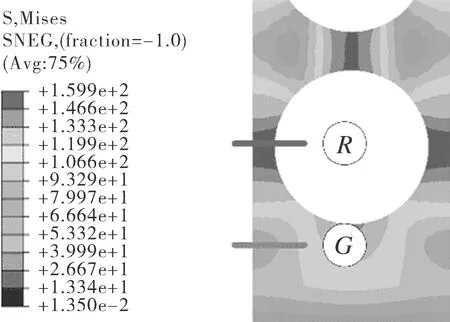
(a)塑性分析

(b)弹性分析图8 热弹塑性分析应力云图Fig.8 Thermo elastic-plastic analysis stress nephogram

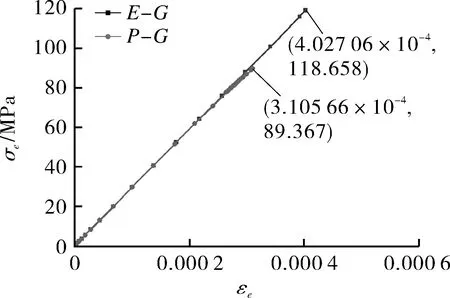
图9 刚性段内壁面应力-应变曲线对比Fig.9 Comparison diagram of stress-strain curve of inner wall surface of rigid section

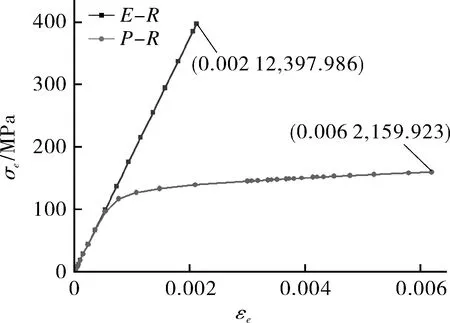
图10 柔性段内壁面应力-应变曲线对比Fig.10 Comparison diagram of stress-strain curve of inner wall of flexible section

为准确表征多轴应力情况下的应力-应变关系，图9、图10中横轴和纵轴分别为等效应变εe和等效应力σe[14]，εe和σe表示方法如下：

(10)

(11)

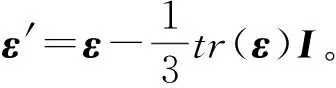
如图9、图10所示，结构局部刚度不连续使刚性段在塑性分析时弹性应力和应变略有下降，而柔性段则产生异常大的应变集中现象。实际上，图9即第1节弹性跟随效应理论阐述中图3的左侧G杆部分，图10为右侧R杆部分。结构外壁面的相关力学现象与内壁面相同。

2.3 残余应力分布结果

在第2.2节仅阐述了满功率阶段结构孔管段的弹性跟随效应，然而孔管型支承结构在快堆中需经受启堆-满功率-停堆的交变高温环境，因此本小节重点分析停堆时结构残余应力产生的原因，并结合第2.2节结构的弹性跟随现象为孔管型支承结构的优化分析做铺垫。塑性分析时Abaqus载荷分析步设置同第2.2节，分析结果如图11所示，图中SNEG代表内表面(图中坐标轴x指向的负方向)，SPOS代表外表面(图中坐标轴x指向的正方向)。

(a)温度平衡阶段

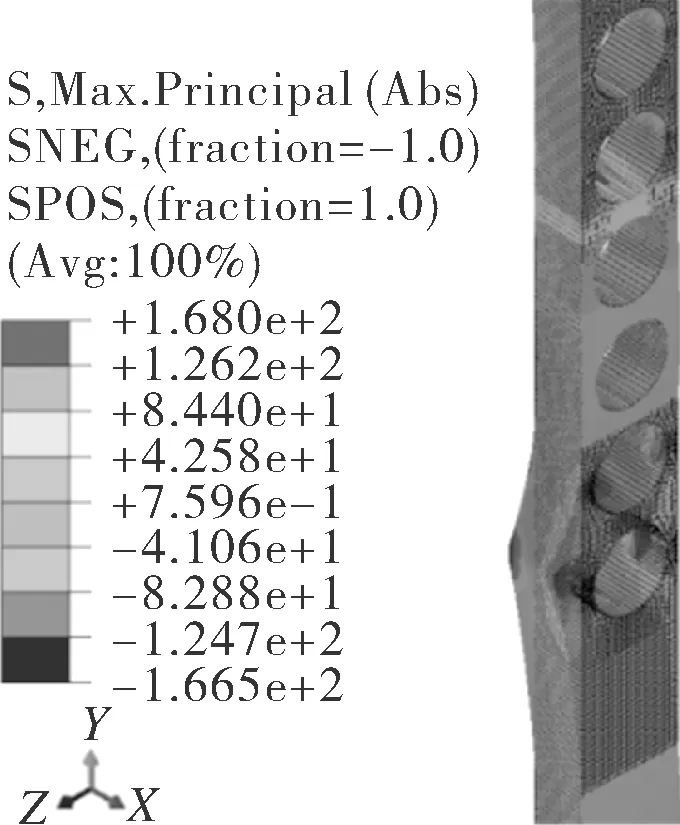
(b)降温阶段图11 结构应力云图Fig.11 Structural stress nephogram

图11(a)中，底端圆孔由于刚度小且温度较上层温度低，在环向位移约束和热膨胀约束情况下产生较高的热应力。图11(b)中，随温度降低，热应变导致的结构弹性应变降低，塑性变形导致的弹性应变增加，残余塑性应变导致结构产生与温度平衡阶段相反的残余应力。

依据降温阶段结束时最大主应力云图，输出节点(结构第一主应力最大处)的绝对值最大主应力、绝对值最大弹性主应变、绝对值最大塑性主应变、绝对值最大热应变和绝对值最大总主应变。

图12为结构内表面绝对值最大主应力。可以看出，在环向位移约束和热膨胀约束情况下升温段结构内表面受拉；降温段结构随温度降低热应变导致的弹性应变降低，塑性变形导致的弹性应变增加，最终残余塑性应变导致结构产生与温度平衡阶段相反的残余应力。结构外表面的现象与内表面相同，但是最大主应力方向相反。该现象在下文基于图13进行解释。

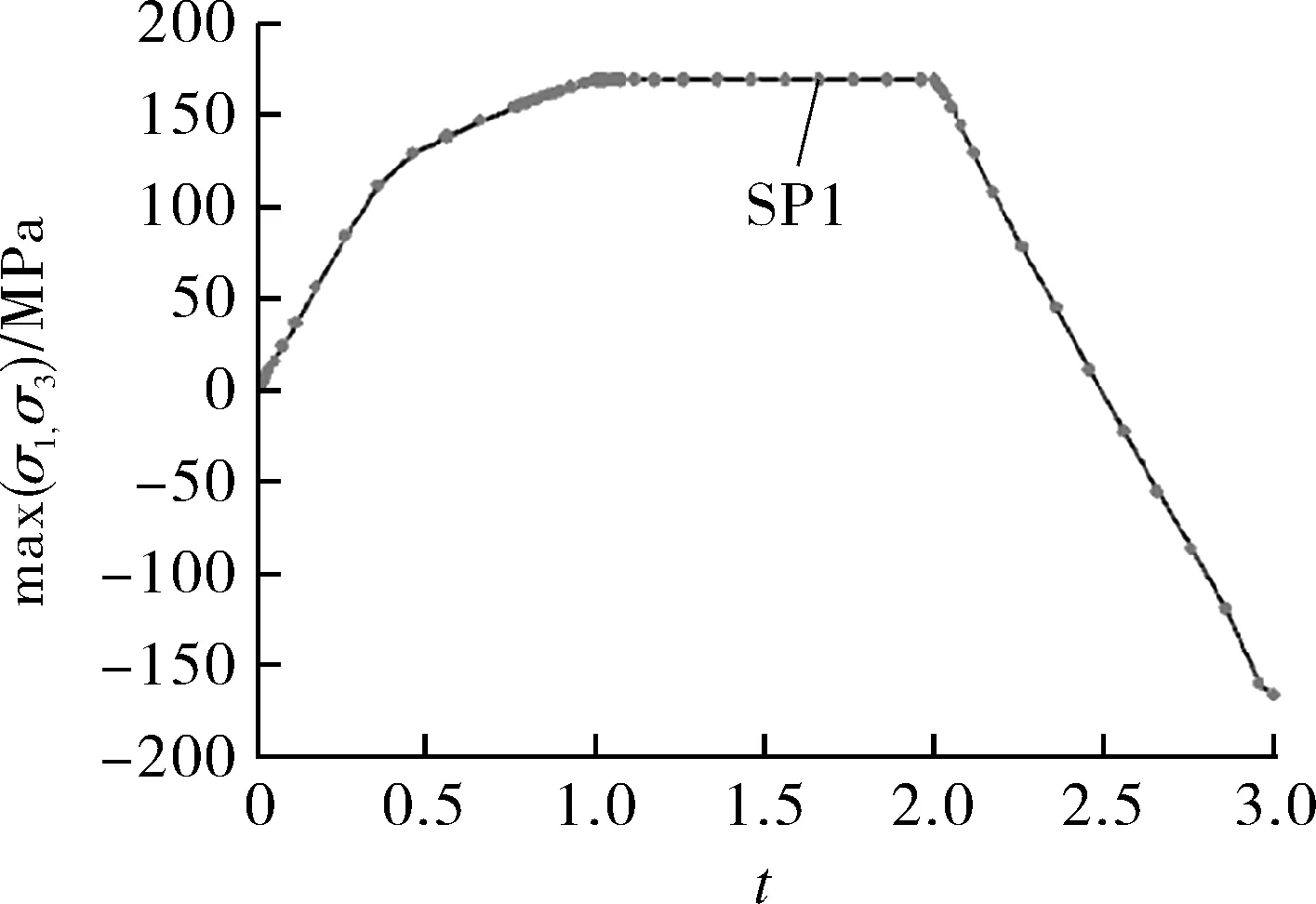
图12 结构内表面绝对值最大主应力Fig.12 Absolute maximum principal stress of inner wall surface of the structure

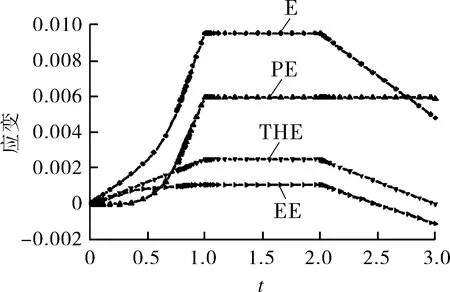
图13 结构内表面绝对值最大主应变Fig.13 Absolute maximum principal strain of inner wall surface of the structure

图13中曲线标注E，EE，THE和PE分别表示结构内表面总应变、弹性应变、热应变和塑性应变的最大绝对值主应变。外表面应变随时间变化曲线同内表面。如图13所示，在升温阶段，结构热应变随温度增加而增加，在环向约束下热应变无法完全释放导致结构内部产生热应力；随温度升高，不断增加的最大绝对值主应变使结构内表面受拉屈服，引起内部塑性应变累积。降温阶段，结构热应变导致的弹性应变随温度下降不断降低，而残余塑性应变导致的弹性应变逐渐增加，最终导致内表面应力状态由受拉转为受压。

由上述讨论可知，孔管段在运行工况下由于冷冲击载荷的作用产生了较大的热应力、塑性应变、残余应力和拉压转换的现象；为延长孔管型支承结构的寿命[15-18]，必须降低孔管段的应力和应变，下文针对孔管型支承结构局部刚度不连续引起的弹性跟随现象对孔管段应力和应变的放大作用进行了分析，同时提出了结构优化的方向。

3 孔管型支承结构弹性跟随效应优化

由上述分析可知，孔管型支承结构局部结构刚度相差较大使结构存在弹性跟随效应，从而导致结构进行塑性分析时产生应变集中现象；结构进行弹性分析时，局部结构柔性部分弹性应力大幅度增加，导致结构较刚度一致时提前进入塑性。即在冷冲击作用下弹性跟随效应的存在使结构产生较大的残余应力和残余应变，影响高温结构性能和寿命。

依据第1节理论，为改善弹性跟随引起的对结构强度和变形的不利影响，采取减薄无孔段降低局部结构刚度差。如图14所示，结构无孔段壁厚设置为10 mm，有孔段为35 mm。

图14 结构优化模型Fig.14 Structural optimization model

降低无孔段刚度之后，首先针对结构进行弹性分析，原结构与优化结构应力值对比见表1。表1中原结构弹性应力最大节点为位于刚柔交界面附近的节点126(即图5所示底端第一个孔水平向右侧减弱位置)；优化结构弹性应力最大位置为远离刚柔交界面的节点39(即图5所示底端第四个孔竖直向上侧减弱位置)。从表1可以看出，通过减少局部结构刚度差可大幅降低结构交界面附近的弹性应力，但远离刚柔交界面的应力下降幅度较刚柔交界面附近应力下降幅度小。造成上述现象的原因主要是在环向约束的情况下，远离刚柔交界面处的区域均为开孔段，弹性跟随效应的影响较弱。

表1 原结构与优化结构应力值对比Tab.1 Comparison of stress values between original structure and optimized structure

由材料屈服强度可知，结构的初始屈服强度为91.186 4 MPa，原结构和优化后结构弹性应力最大值均已超初始屈服强度，升温阶段结构轴向温差梯度引起的热应力导致结构进入屈服状态。因此采用第2.1节塑性本构对结构进行弹塑性分析，不同阶段原结构与优化结构Mises应力最大值对比见表2，累积塑性应变对比见表3。

表2 不同阶段原结构与优化结构应力值对比Tab.2 Comparison of stress values between original structure and optimized structure in different stages

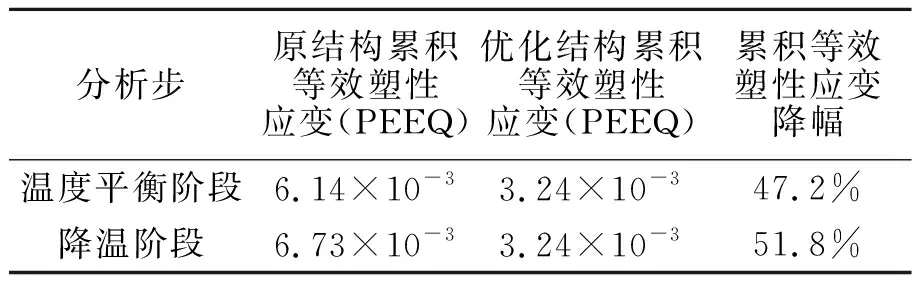
表3 不同阶段原结构与优化结构累积等效塑性应变对比Tab.3 Comparison of cumulative equivalent plastic strain between original structure and optimized structure in different stages

由表2可以看出，原结构在降温阶段产生反向屈服，导致降温阶段应力增加；由于优化结构降低了结构应力，因此无降温阶段应力增加的现象。由表3可知，原结构由于热应力导致的残余塑性应变较大，因此在降温阶段导致结构反向屈服，从而使得等效累积塑性应变增加；由于优化结构降低了结构应力，因此无降温阶段结构反向屈服现象。

由上述分析可知，通过优化结构刚度分布，改善结构刚度不均匀特性可以显著降低结构的塑性应变，从而使得结构满足工程上的变形限值。在塑性分析中，结构应力变化不明显的原因主要是塑性强化本构的切线模量很低，因此优化结构相对于原结构的应力增量与当前应力的比值远低于累积等效塑性应变增量与当前应变的比值。