基于ASME Ⅷ-1—2017标准的爆破片装置泄放能力计算方法研究

吴全龙，孙少辰，后文杰，史斐菲

(1.上海华理安全装备有限公司，上海 201108；2.沈阳特种设备检测研究院，沈阳 110179)

符号说明：

A——有效泄放面积，mm2；

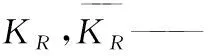
ea——流阻系数平均偏差；

KD——泄放系数；

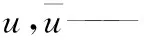
ρ——密度，kg/m3；

ΔP——压降，kPa；

Δp——压降，Pa；

W——计算流量，kg/h；

W1——实测氮气流量，kg /h；

WT——理论流量，kg/h；

G——质量流速，kg/s·m2；

d——管道名义内径，mm；

K——泄压系统总流阻系数；

v——泄放状态下介质的比容，m3/kg；

Y—— 气体膨胀系数；

k——气体绝热指数；

P0——容器泄放压力绝对值，kPa；

P1——管道入口压力绝对值，kPa；

p1——管道入口压力绝对值，Pa；

P2——管道出口压力绝对值，kPa；

p2——管道出口压力绝对值，Pa；

Psonic——临界流动压力，kPa；

Ysonic——气体临界膨胀系数；

T0——容器泄放温度，K；

T1——管道入口温度，K；

T2——管道出口温度，K。

0 引言

ASME Ⅷ-1—2017ASMEBoiler&PressureVesselCode,SectionⅧ,Division1,RulesforConstructionofPressureVessels规定，爆破片装置作为承压设备单独泄放装置时，根据上下游进出口管道结构尺寸的不同，应选用不同的泄放能力(泄放量)计算方法：流阻系数法或泄放系数法，与两种方法相对应的爆破片装置产品应分别认证标定流阻系数和泄放系数。

ASME Ⅷ-1未给出流阻系数法计算公式，工程中通常以API 520-1—2020Sizing,Selection,andInstallationofPressure-RelievingDevices附录E的计算实例作为参考。泄放系数法的理论流量计算公式以绝热等熵喷嘴模型为基础，对泄压系统进出口管道的结构尺寸、泄放介质特性也有很多限制，其中理论流量的计算和泄放系数的测定都应符合相应假设[1-6]。

文中以ASME Ⅷ-1为基础，通过理论分析、公式推导和试验数据对比两种方法的应用范围及使用限制条件进行探讨。为叙述方便，文中将包括上下游进出口管道在内的爆破片装置统称为泄压系统。

1 流阻系数法

流阻系数法综合考虑泄压系统直管阻力、弯头、三通、异径管、阀门和爆破片装置等管道配件引起的流体阻力损失影响，以伯努利能量守恒方程为理论基础计算泄放量，具有广泛的通用性，适合于任何泄压系统。采用流阻系数法计算泄放量时，爆破片装置流阻系数KR是非常重要的技术性能参数。

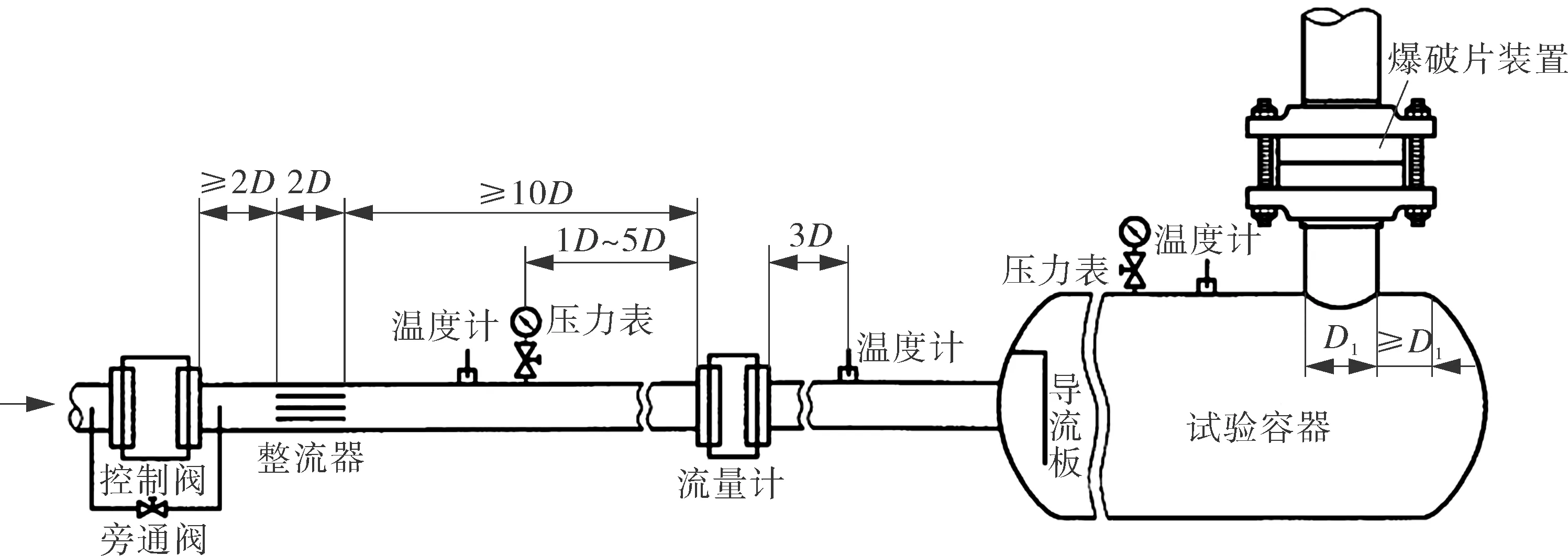
ASME PTC25—2014PressureReliefDevicesPerformanceTestCodes、GB/T 567.4—2012《爆破片安全装置第四部分：型式试验》 等标准认证测定KR的试验装置如图1所示，更详细内容可参考文献[7-9]。下面以某公司RM90(反拱带槽型)爆破片装置“UD”取证试验数据为例对KR测定过程进行分析。

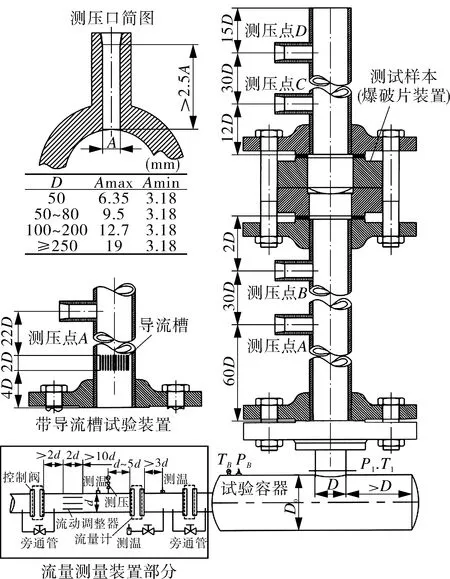
图1 爆破片装置流阻试验装置Fig.1 Arrangements for testing flow resistance of rupture disk devices

1.1 流阻系数测定试验数据分析

按三规格法测定KR时，提供了公称尺寸为25,40,50 mm三种口径的爆破片装置，每种口径3片、总计9片样品用于试验，参照表1序号1～3。流阻系数测定值与爆破片破裂后的几何形状密切关联，爆破压力越低，爆破片开启程度越受限，因此，试验样品中的设定压力应为该设计口径产品中制造厂家所允许制造的最小设计爆破压力。同时,考虑试验装置的能力限制(尤其是气源限制)，样品最大口径不大于50 mm。为便于后续分析，将口径40 mm的样品测定数据汇总如表2所示。

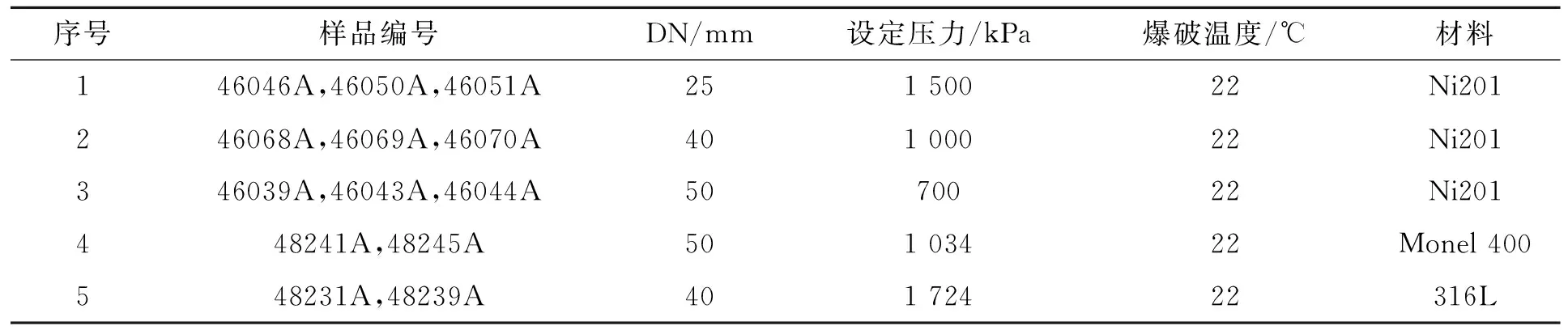
表1 爆破片样品参数Tab.1 Table of parameters of rupture disc sample

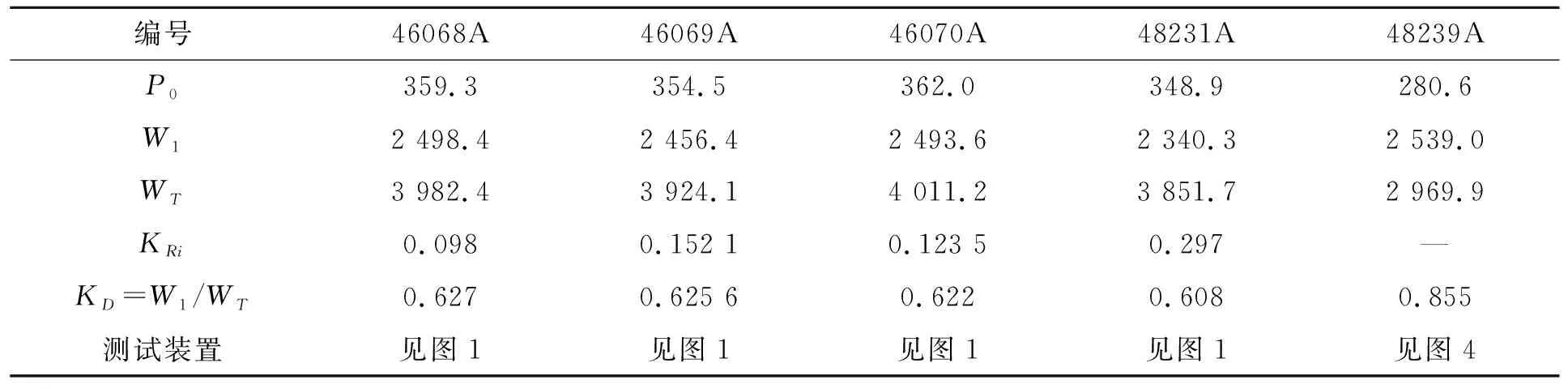
表2 爆破片装置流阻系数试验结果Tab.2 Flow resistance coefficient test results of rupture disk devices

ASME Ⅷ-1 UG-131中给出了流阻试验数据处理方法，结合ASME PTC25和GB/T 567.4的规定，爆破片装置流阻系数试验结果分析程序如下[7-8]。

(1)根据试验样品测试值计算平均流阻系数和平均偏差，即:

(1)

(2)

(2)每一片爆破片的流阻系数应按下式进行合格性判断：

(3)

(3)如果都满足公式(2)的要求，则该设计结构的爆破片装置流阻系数可按以下公式取值：

(4)

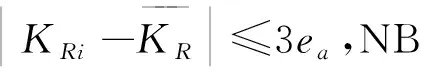
表3 爆破片装置流阻系数计算结果Tab.3 Table of calculated flow resistance coefficients for rupture disk devices

1.2 泄放量计算公式推导与分析

图1所示爆破片装置流阻系数测试装置是一个典型的任意泄压系统，测试装置的介质流动状态如图2所示。截面1-1和截面2-2分别为管道入口和出口。由于排放时间较短，流动可视为绝热等熵膨胀过程，所有试验数据在达到稳态流动时采集记录，属于一维稳态管流。

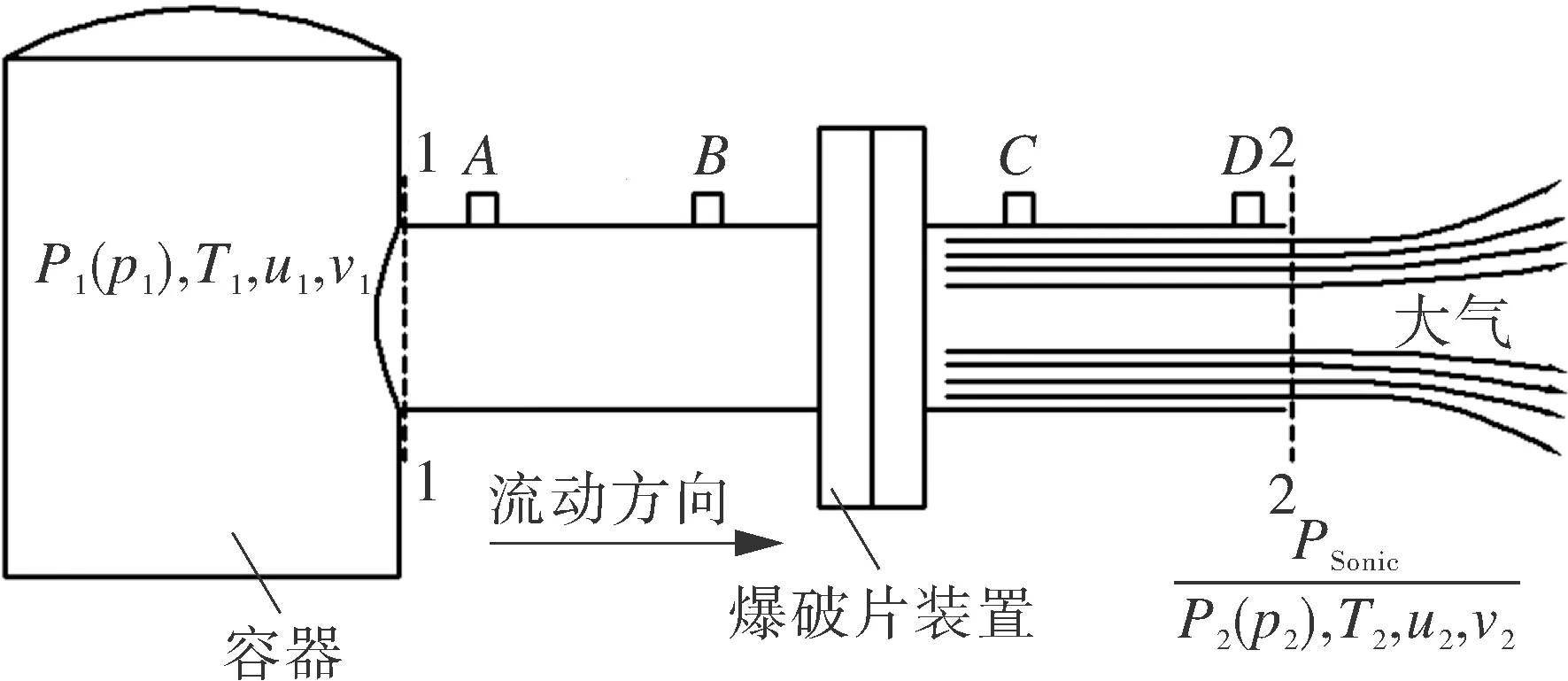
图2 流阻系数测试装置介质流动状态简图Fig.2 Schematic diagram of medium flow of the test rig for flow resistance coefficient testing

根据伯努利能量守恒方程，对于截面1-1和截面2-2有：

(5)

上式中hf为因摩擦阻力导致的能量损失：

(6)

将式(6)代入式(5):

(7)

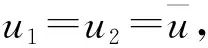
化简上式，可得：

从而有：

(8)

将式(8)中Δp(压力单位Pa)转换成ΔP(压力单位kPa)，并计算泄放量：

(9)

式(9)为适用于液体介质流阻系数法泄放量计算公式。

气体从相对较短的管道排放至更大空间(比如大气)，气体的流速、比体积、压力沿着管道改变，随着压力降低，流速和比体积增大，容易产生临界流动(流速超过当地声速)。到达临界流动后，即使下游压力继续降低，流量也不会持续增大，此时的压力称为临界流动压力Psonic，流量为相应排放压力下的最大值。考虑到以上因素，对于绝热等熵膨胀过程，在式(9)中应引入气体膨胀系数Y:

(10)

式(10)即为API 520附录E中公式(E.6)转换为SI单位后的表达形式(未考虑0.9的工程校正系数)。Y的取值与气体绝热指数k、总流阻系数K和ΔP/P1有关，CGA S-1.3—2020PressureReliefDeviceStandardsPart3—StationaryStorageContainersforCompressedGases给出了气体膨胀系数Y的计算公式(注意K和k的区别)[10]：

(11)

求解一定条件下的气体泄放量,即根据式(10)(11)找到出现临界流动的压力Psonic及相应的Y值，但过程非常复杂，需要进行迭代计算。

当k=1.4时，式(11)可简化成：

(12)

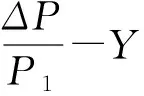
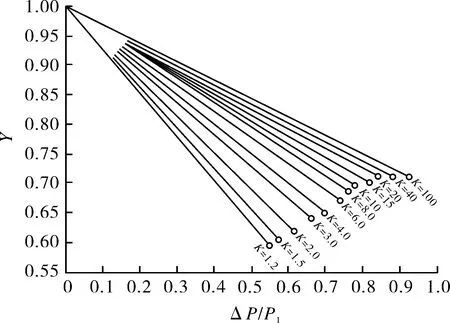
图3 气体净膨胀系数Y值(k=1.4)Fig.3 Value of gas net expansion factor Y (k=1.4)

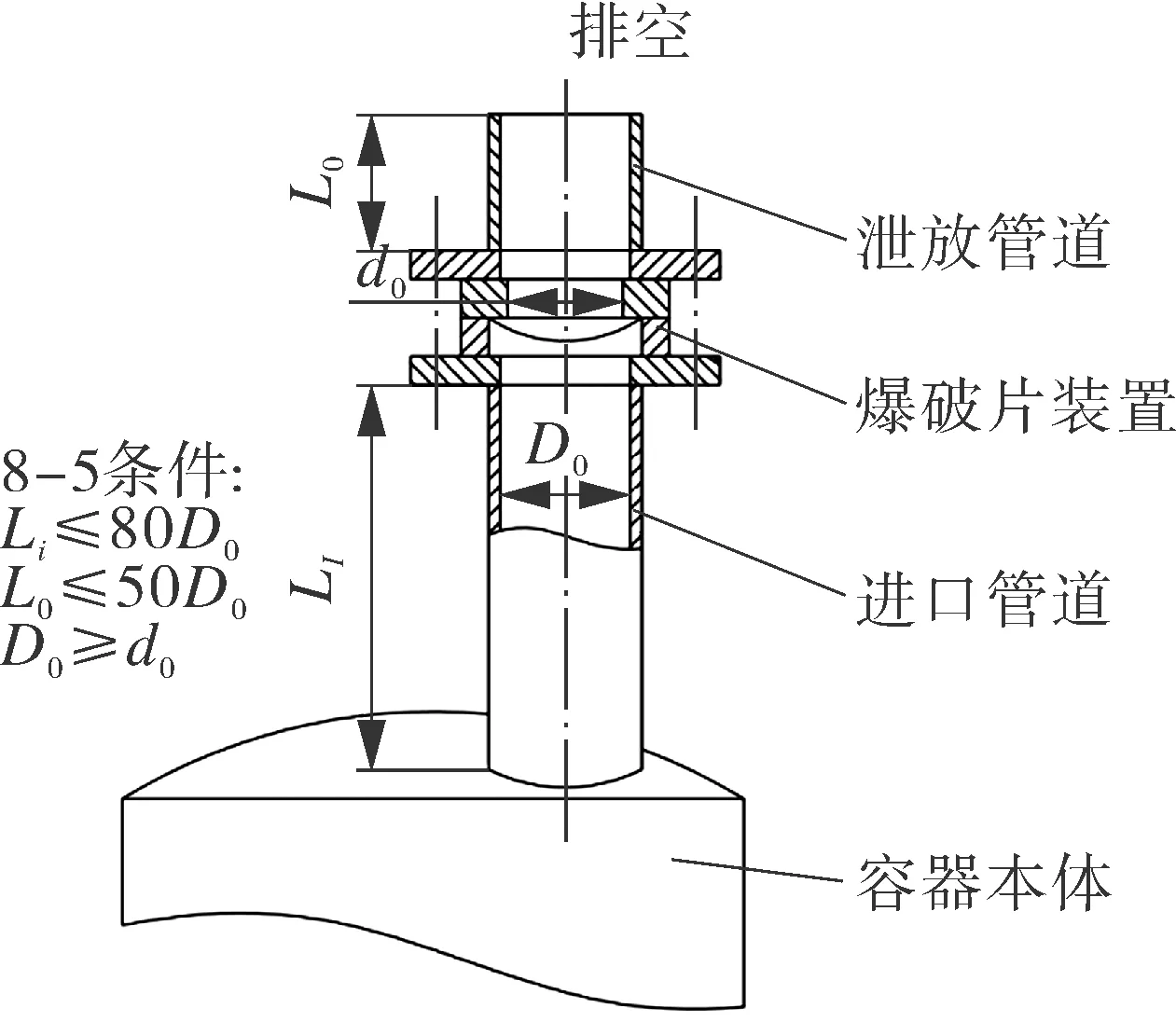
API 520附录E进一步归纳了气体绝热指数为1.4时，不同流阻系数的ΔPsonic/P1值及相应的Ysonic简化计算公式： 当1.2

ΔP/P1>ΔPsonic/P1时，为临界状态，在式(10)计算时，Y和ΔP分别用Ysonic和ΔPsonic替代。反之，为亚临界状态，应根据管道总流阻系数K，ΔP及Y代入式(10)进行计算，相关参数取值可通过图3查得。

由于管道入口处各技术参数未知，工程中一般采用达到稳定泄放状态下时的容器内参数代替，即ΔP=P0-P2，比体积为容器泄放状态下的比体积，K为P0至P2的总阻力系数(包括入口侧突然缩小造成的阻力损失)。

1.3 计算举例

以表1中编号46070A实际测量数据为例，按式(10)计算流阻系数测量试验装置中的泄放量，并将计算值与测量值进行比较。

根据试验报告，可知相关参数为：P1=325.13 kPa(abs)；T1=280.9 K；K=3.4387；v=0.245 m3/kg。

首先判断流动是否达到临界状态： ΔPsonic/P1=0.671 9，ΔP/P1=0.693， ΔP/P1>ΔPsonic/P1，流动达到临界状态，从而：ΔPsonic=218.45 kPa(abs)，Ysonic=0.642 5，由此求得：W=2 195.8 kg/h。

从表2可知，实际测量的泄放量W1=2 493.6 kg/h，计算结果和实测值很接近，误差为-11.9%。

根据上述计算结果，Psonic=107.0 kPa，而试验报告提供的测压点A，B，C，D压力值分别为264，238，213，170.5 kPa，直至测压点D仍未产生临界流动，最终在管道出口处才到达临界压力。

如果采用容器泄放状态下的压力、温度、比容分别代替管道入口处相应参数，计算结果如下：d=40.97 mm；P0=362.18 kPa(abs)；T0=289.89 K；K=3.938 7；v=0.211 m3/kg。

首先判断流动是否达到临界状态：

ΔPsonic/P0=0.686 9，ΔP/P0=0.723 9,ΔP/P0>ΔPsonic/P0，流动达到临界状态，从而ΔPsonic=248.78 kPa(abs)，Ysonic=0.648 4，从而求得：W=2 381.0 kg/h。

两者的计算结果相差约为8.5%，后者与实际测量值的误差为-4.5%。

2 泄放系数法

工程中常见的泄压系统进口管道和出口管道相对较短，这类泄压系统虽然也可采用流阻系数法确定泄放量，但由于不同绝热指数对应的Ysonic和ΔPsonic/P0较难获得，过程繁琐复杂，通常可按泄放系数法进行计算，即：

W=KDWT

(13)

式中,KD为泄放系数;WT为理论计算流量。

2.1 理论流量的计算

根据API 520 PART 1附录B可知，ASME Ⅷ-1 UG-131中不同介质的理论流量计算公式是基于以下假设通过热力学分析求得[10-12]：

(1)忽略介质的黏度影响，或者说介质为理想状态；

(2)泄压系统几何模型为喷嘴(Isentropic nozzle)、孔板(Orifice)或短管(Short pipe)；

(3)流动为可逆绝热过程；

(4)计算结果为稳态流动时的理论最大流量。

显然，实际泄压系统和泄放介质与理论流量计算时的假设有差异，例如，进出口管道几何结构、尺寸大小、摩擦系数的不同及泄放介质通常有黏度。因此，实际流量与理论流量相比，存在以下两方面的影响因素：

(1)实际泄压装置与理论模型之间几何结构及摩擦系数的差异；

(2)实际流体与理想流体黏度的差异。

这些影响因素带来的误差可通过泄放系数进行修正。

2.2 泄放系数KD

ASME Ⅷ-1—2010开始提出采用与测定安全阀额定泄放系数相同的试验装置、试验方法对爆破片装置进行额定泄放系数认证测定，ASME Ⅷ-1—2013进一步规定可在爆破片铭牌上标识相应的额定泄放量。这些规定具有重要意义，符合当今节能减排的设计理念，ASME Ⅷ-1—2017延续了相关要求。

KD本质上反应了实际泄压系统相对于理论流量计算模型整体阻力损失，大小与测试装置的几何结构尺寸和光洁度(摩擦系数)密切相关。泄放系数是实测流量与按相关几何模型计算的理论流量比值，因此，测试装置的泄压系统应尽可能满足以下条件[13]：

(1)进出口管道结构应尽可能接近理论流量计算时的几何模型；

(2)进出口管道结构应尽可能覆盖工程实践中的实际泄压系统结构；

(3)在满足(2)时，进出口管道引起的阻力损失尽可能小。

按照以上原则，ASME PTC 25中Fig.4-2.3-1安全阀泄放系数测定装置对测试元件的进出口管道有严格规定，出口管道长度不大于被测试泄压装置公称口径的5倍，进口管道应符合ASME PTC 25中Fig.4-2.10-1要求。爆破片装置泄放系数测试装置如图4所示，与ASME PTC 25 Fig.4-2.3-1类似，测试元件进出口管道结构尺寸也应尽可能满足喷嘴结构要求。

图4 泄放系数测定试验装置Fig.4 Test device for coefficient of discharge

进行流阻试验时，试验报告也会给出一KD值，但由于试验装置出口排放管较长，阻力损失较大，所以泄放系数可能较小，例如表2中在图1装置试验的各样品泄放系数平均值为0.621，而在图4装置试验的样品48239A的泄放系数为0.855。这表明，同一设计类型的爆破片，在不同结构(特别是进出口管道结构)的试验装置上，测定的KD值不同。

2.3 泄放系数法使用条件

通过前面的分析可知，理论流量的计算基于假定的理想模型，泄放系数测试装置的测试样品进出口管道结构尺寸对测定的KD值大小有重要影响。对于安全阀，无论是实际产品结构还是泄放系数测定装置结构均接近于理想喷嘴模型，但是对于单独设置爆破片装置的泄压系统，进出口管道一般不是爆破片制造厂家直接提供，为了使实际泄压系统能满足理论流量计算及泄放系数测定的相关要求，在使用泄放系数法计算泄放量时，应保证泄压系统满足如下条件(简称为“8-5条件”，如图5所示)：

图5 8-5条件Fig.5 8-5 conditions

(1)爆破片装置直接排放至大气；

(2)爆破片装置离容器本体距离不超过8倍管径；

(3)爆破片装置泄放管道长度不超过5倍管径；

(4)爆破片装置上、下游接管的名义直径不小于爆破片装置的泄放通径。

“8-5条件”的实质是使设置爆破片装置的泄压系统与理论流量计算模型和KD测试装置结构无限接近，从而可采用式(13)确定泄放能力。另外，由于实践中的泄压系统进出口管道尺寸大多都不超过“8-5条件”中规定的最大值，因此，在工程中有较大覆盖性。

ASME Ⅷ-1 UG-127规定，对于仅标定泄放系数时爆破片装置泄放量的计算，应根据测定的泄放系数、爆破片装置进出口管道元件和介质特性综合考虑，但具体计算方法并未明确。ASME中符合“UD”标识要求的爆破片装置的标定KD值在如图4所示试验装置测定，理论流量按等熵喷嘴模型计算，因此，笔者认为，ASME Ⅷ-1 UG-127(a)(2)(-b)中的实际泄压系统应该满足 “8-5条件”，并可根据标定的KD值采用式(13)进行泄放量计算。

对于仅标定流阻系数的爆破片产品，按泄放系数法(取默认泄放系数0.62)计算泄压系统泄放量时，ASME Ⅷ-1 UG-127(a)(2)(-a)(-1)明确规定，泄压系统应满足“8-5条件”。表2中编号48231A样品在图1装置(不满足“8-5条件”)中测出的KD=0.607，也用试验数据验证了这一条件的必要性。当泄压系统不满足“8-5条件”时，如果根据泄放系数法计算泄放量，可能导致选择的爆破片口径偏小，给被保护承压设备带来安全隐患。工程中的泄压管道，阻力损失可能远大于图1所示装置，这类隐患不容忽视。

根据第2.2节关于KD测定的分析可知，测试装置中泄压系统进出口管道的长度对最终测定结果有较大影响，因此，为了使测定结果适用于“8-5条件”的泄压系统，测试装置中泄压系统进出口管道的长度应不低于“8-5条件”规定的最大值，但也不应超出过多，否则，由于增加管长加大了阻力损失将导致测定值偏保守。

3 流阻系数法与泄放系数法的比较

流阻系数法泄放量的计算可采用式(9)和式(10)，对于气体介质涉及到膨胀系数Y，需要通过迭代求解，计算过程很复杂。满足“8-5条件”的泄压系统，将阻力损失统一到经试验认证测定的泄放系数，按泄放系数与理论流量的乘积计算泄放量，简化了计算过程。

当爆破片装置仅标定流阻系数时，对于采用爆破片装置作为单一超压泄放装置的压力系统可取默认泄放系数，KD=0.62。基于这一原因，对进行流阻试验测定认证的爆破片装置，需在图4所示的试验装置验证默认泄放系数是否符合要求，如表2中编号为48239A的试验数据就是单片爆破片的完整泄放系数测定结果。图4试验装置实际上是一满足“8-5条件”的特殊任意压力系统，也可按式(10)采用流阻系数法计算泄放量。因此，可通过编号48239A样品试验数据来对两种方法的计算结果进行比较。

图4所示试验装置中进出口管道较短，可忽略直管阻力影响，仅考虑进口突然缩小、出口突然放大及爆破片装置的流阻即可，即总的流阻系数K=1.8(爆破片实际流阻系数假设为0.15)。根据试验报告，相关参数为：d=39.76 mm；P0=280.1 kPa(abs)；T0=288.5 K；K=1.65；v=0.308 m3/kg。

首先判断流动是否达到临界状态：ΔPsonic/P0=0.59，ΔP/P0=0.642，ΔP/P0>ΔPsonic/P0，流动达到临界状态，从而得到：ΔPsonic=165.4 kPa(abs)，Ysonic=0.611，W=2 202.6 kg/h。

从表2可知，48239A样品的理论流量为2 970 kg/h，实测流量为2 539 kg/h。如果采用泄放系数法计算泄放量，当泄放系数默认为0.62时，结果为1 841 kg/h，当采用测定的泄放系数值时(0.9×0.855)，结果为2 285 kg/h，按流阻系数法计算结果为2 202.6 kg/h，如表4所示。从表中数据可以看出，流阻系数法与采用实测KD的泄放系数法计算结果较为接近，但采用默认泄放系数计算泄放量，计算结果偏保守。

表4 两种计算方法的综合比较Tab.4 Comprehensive comparison of the two methods

4 结语

现行标准中，符合“UD”要求的产品一般只需认证标定流阻系数，泄放系数默认为0.62。但实际工况中，设置爆破片装置的泄压系统普遍符合“8-5条件”，当未标定泄放系数时，通常也取KD=0.62，然后乘上相应的理论流量作为实际排量，这种简化将导致选择过大口径的爆破片，不利于节省成本和低碳排放。同样，如果仅标定泄放系数，对于不符合“8-5条件”的压力系统按标定的KD计算泄放量，将导致选择的爆破片口径过小，带来安全隐患。因此，从经济性和安全性的角度考虑，爆破片装置应将KD和KR都强制标定，便于工程设计人员根据不同的泄压系统选用不同的计算方法。

国内标准GB/T 150.1—2011附录B和GB/T 567系列，均未对爆破片装置的泄放系数测定方法作出规定，关于如何使用流阻系数进行泄压系统泄放量的计算，国内标准也尚无介绍。论文有助于国内标准补充完善这些技术要求。