分数阶混沌系统自适应有限时间追踪控制
2022-02-17李贤丽汤俊杰朱金元温玉玉
李贤丽,汤俊杰,朱金元,温玉玉
(东北石油大学物理与电子工程学院,黑龙江大庆 163318)
分数阶微积分理论始于17 世纪,但最近几十年才得到研究者的关注。一方面分数阶微积分理论将整数阶微积分推广到任意阶次可以更准确地描述动力学现象,如机械系统、生物工程和流体力学等。另一方面,许多分数阶系统中都存在混沌现象,如分数阶统一混沌系统[1]、分数阶Lorenz 混沌系统[2]、分数阶Rossler 混沌系统以及分数阶金融混沌系统[3]等。
近年来,将分数阶微积分理论应用在混沌控制中已经成为物理、数学等领域的研究热点。许多控制方法相继提出,如线性反馈控制[4]、追踪控制[5]、自适应控制[6]、脉冲控制[7]、滑膜控制[8]等。滑膜控制是一种简单实用的混沌控制方法,因其具有较强的抗干扰能力而得到广泛关注。这些混沌控制方法大多是渐进稳定的,而有限时间控制可能在实际应用中更有意义,因此在20 世纪中期Kamenkov 首次提出有限时间稳定概念,不仅使受控系统具有更快的收敛速度,而且具有较强的鲁棒性以及抗干扰能力。Amato[9]和Garcia 研究了连续时间及离散时间系统的有限时间稳定问题。Wang[10]等人解决了超混沌系统的有限时间控制问题。2018 年,邵克勇[11]等人成功将整数阶混沌系统有限时间控制理论推广到分数阶混沌系统,实现了分数阶超混沌Lorzen 系统有限时间控制。但是上述研究只是将混沌系统控制到零点,将混沌系统控制[12]到任意点的研究较少。文中基于有限时间控制理论,结合追踪控制法,对参数未知的分数阶Zhang 混沌系统进行控制研究,通过设计自适应有限时间追踪控制器,实现了系统的自适应有限时间追踪控制。实验结果表明,该方法可以使系统状态变量在有限时间内收敛到任意点,并且具有较强的抗干扰能力。
1 分数阶微积分概述和基本理论
当前分数阶微积分定义主要分为3 种,分别是Riemann-Liouville 定义[13]、Grunwald-Letnikov 定义以及Caputo 定义。文中采用Caputo 定义。
定义1 连续函数f(t)的q阶Caputo 分数阶导数定义为:

式中,q是分数阶系统的阶次,满足n-1 ≤q≤n,Γ(∙)是Gamma 函数。
定义2 Gamma 函数[14]定义为:

引理1 假设x(t)∈Rn是连续可导的,则对于任意时间t≥0,∀q∈(0,1),有:
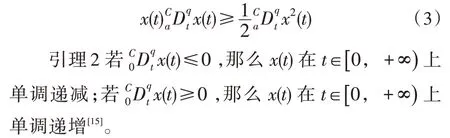
引理3 假设存在一个Lyapunov函数V(t,x(t)),m和n为任意正常数,且存在一个类β函数βi(i=1,2,3)满足下列不等式,则该系统满足全局Mittag-Leffler稳定。

引理4 如果系统Dqx(t)=f(t,x(t))满足引理3 且满足DqV(t,x(t))≤,则说明该系统是有限时间内稳定的,且系统的稳定时间满足:
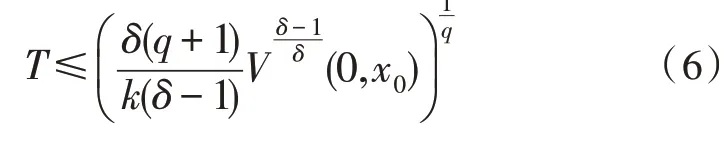
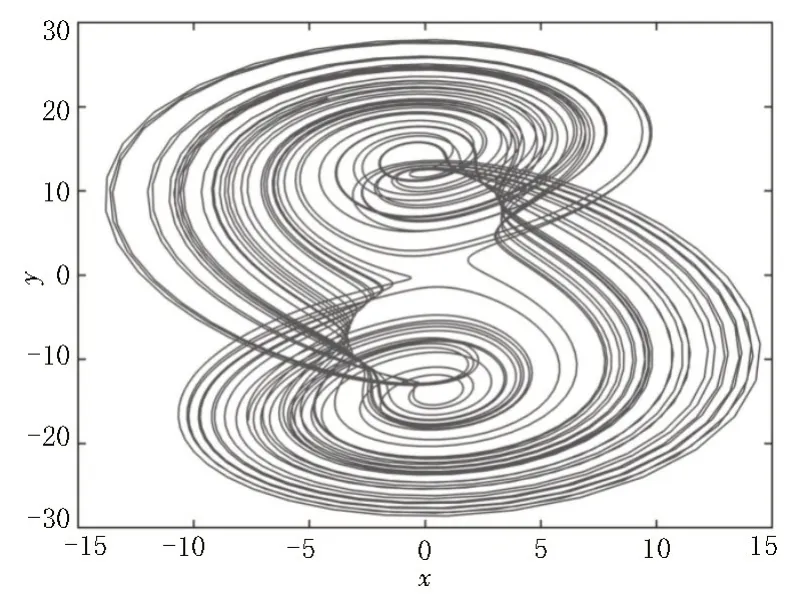
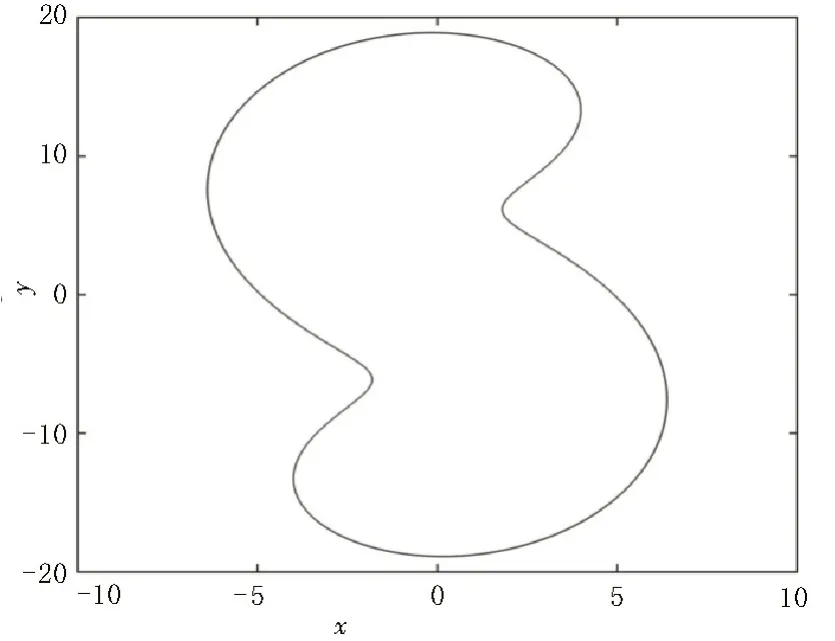
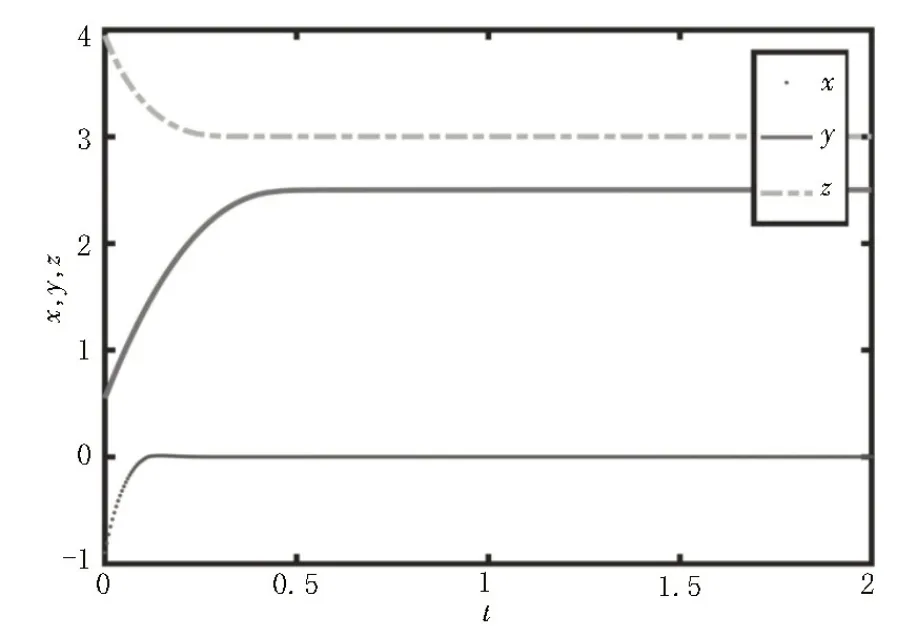
其中,q是阶数且0 引理5[16]假设xi=x1,x2,…,xn是实数,且0 文中以分数阶Zhang 混沌系统[17]为研究对象,其数学模型如下: 设定分数阶Zhang 混沌系统的参数为a=12,b=25,c=8,阶数q=0.95,初始值x0=-1,y0=0,z0=1,通过MATLAB 进行数值计算,得到分数阶Zhang 混沌系统随参数d变化的分叉图如图1 所示。 图1 分数阶Zhang混沌系统分叉图 从图1 可知,当d∈[0,1.87)时系统处于混沌状态,取参数d=1,系统的二维相图如图2 所示;当d∈[1.87,2.05)时系统处于周期状态,取参数d=2,系统的二维相图如图3 所示;当d∈[2.05,2.5)时系统处于混沌状态,取参数d=2.3,系统的二维相图如图4 所示;当d∈[2.5,6)时系统处于周期状态,取参数d=6,系统的二维相图如图5 所示。 图2 d=1时系统二维相图 图3 d=2 时系统二维相图 图4 d=2.3 时系统二维相图 图5 d=6 时系统二维相图 令式(8)左边为零,可以求得系统的平衡点,则其平衡点处的Jacobian 矩阵为: 根据分数阶稳定性定理可知,为了保证系统在平衡点处渐进稳定,就需保证其平衡点处Jacobian矩阵的特征值(λ1,λ2,λ3)满足|arg(λi) |>πα/2,α=max(qi),i=1,2,3,通过数值计算可知,当式(9)的阶数为qi(i=1,2,3)<0.846 161 时,可满足条件。 分数阶Zhang 混沌系统表达式如下: 其中,xi(i=1,2,3)是系统的状态变量,ui(i=1,2,3)是待设计的控制器,a、b、c分别为系统的未知参数。当不考虑控制器时式(9)满足分数阶Zhang 混沌系统结构。 当系统参数为a=12,b=25,c=8,阶数q=0.95时,系统处于混沌状态。选取上述参数,选取初始值x1=1,x2=0,x3=1 时,分数阶Zhang 混沌系统相图如图6 所示。 图6 分数阶Zhang混沌系统相图 式(9)满足的自适应有限时间追踪控制器描述如下: 在满足式(10)的控制器作用下,满足式(9)的系统是有限时间稳定的。其中ki>0(i=1,2,3),0<λi<1(i=1,2,3),a1、b1、c1是a、b、c的估计值,e1=x1-y1,e2=x2-y2,e3=x3-y3,其中yi(i=1,2,3)为给定的常数追踪信号。参数更新规则如下: 其中,ki>0(i=4,5,6),λi(i=4,5,6) 为任意实数,不确定参数的估计误差为ea=a-a1,eb=b-b1,ec=c-c1。 证明:选取Lyapunov 函数 由式(9)~(13)可得: 由于ki>0(i=1,2,3,4,5,6),可得DqV≤0。因为DqV≤0,所以一定存在β3>0,使得DqV(t,e)≤-β3‖e‖2,故由引理3 可知,式(9)满足的系统是Mittage-Leffler稳定。且由DqV(t,e)≤0 可得=0,因此,该控制器可以保证系统的解全局有界。同时由式(12)可得≤2V(0,e)。当≤1 时,有: 因此,若初始条件满足: 时,由于DqV≤0,所以e(t)∈Ω。因此,对任意初始条件e(0)∈Ω都有: 由引理4 可知,系统DqV1是有限时间稳定的,因为DqV(t,e)是全局Mittag-Leffler 稳定且DqV1中所有的初值都包含在DqV(t,e)内,所以DqV(t,e)是有限时间稳定的。 为证实参数未知的分数阶Zhang 混沌系统的有限时间追踪控制器和自适应率的有效性,对其进行数值仿真,系统参数设置为a=12,b=25,c=8,q=0.9;未知参数初始值a1=8,b1=27,c1=6,ki=6,λi=0.5(i=1,2,3,4,5,6),初始条件为x0=(-1,0.5,4),给定信号y0=(0,2.5,3),稳定时间t≤1.55 s,仿真结果如图7 所示。 图7 状态变量时序仿真 由图7 可知,系统在1.55 s 内便消除了混沌,状态变量在有限时间内收敛到追踪信号y0=(0,2.5,3),同时实现了对未知参数的辨识。 为证明该方法具有抗干扰性,给出扰动模型如下: 其中,k1=0.2,k2=0.3,k3=0.1,其余参数不变,仿真效果如图8 所示。仿真结果表明,当初始条件完全一致的情况下加入有界随机噪声的情况下,该系统在1.55 s 内收敛到追踪信号,证明了文中设计控制器的有效性和良好的抗干扰能力。 图8 状态变量时序仿真 文中基于分数阶微积分理论及有限时间控制理论和追踪控制原理,通过设计自适应有限时间追踪控制器,实现了参数未知的分数阶Zhang 混沌系统的追踪控制。仿真结果表明该方法简单有效,可以使受控系统在有限时间内收敛到任意点,收敛速度较快。引入有界随机噪声,证明该方法具有良好的抗干扰能力。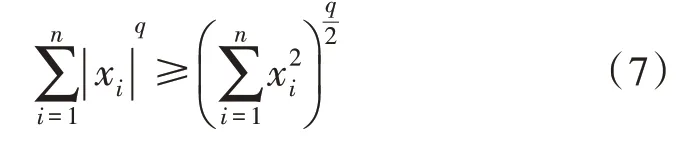
2 分数阶Zhang混沌系统动力学动力学性质分析
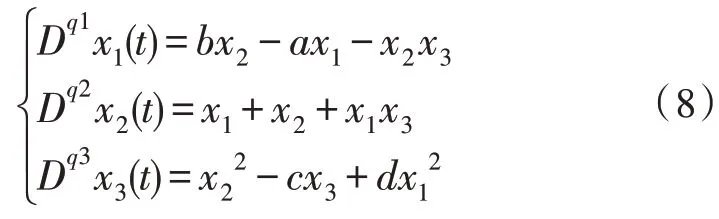




3 自适应有限时间追踪控制







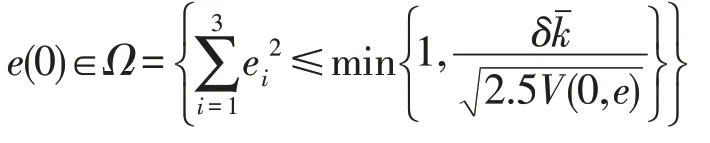

4 数值仿真


5 结论
