钢筋钢纤维混凝土梁柱节点模型化方法研究

薛 茹， 刘晨晨， 赵雯桐， 史 科， 张 涛， 管巧艳

(郑州航空工业管理学院 土木建筑学院，郑州 450046)

梁柱节点作为框架结构传递和分配内力的枢纽，是核心受力部位和震害易受损区域。钢纤维混凝土具有优良的受弯、受剪和高韧性等性能，可明显提高梁柱节点的抗震性能[1]。针对钢筋钢纤维混凝土(steel fiber reinforced concrete，SFRC)梁柱节点的抗震性能，国内外学者已进行了大量的试验，积累了较为丰富的试验数据，但相关研究主要集中于钢纤维体积率对抗震性能的影响。数值模拟技术，可更为系统地分析较多抗震性能影响因素，同时能够较精确的详细研究节点核心区材料的受力状态和行为，为梁柱节点的抗震机理分析提供依据。因此，有必要结合钢纤维混凝土受力特性，研究精细高效的梁柱节点抗震性能数值模拟技术。

地震作用下，节点核心区的非弹性变形尤其是剪切变形和纵筋黏结滑移变形，是梁柱节点抗震性能数值模拟的关键。对此，学者提出了不同的模型化方法。杨红等[2]在梁端部设置弹塑性转动弹簧用来模拟节点区的纵筋黏结滑移变形；Alath等[3]在节点区附加非线性转动弹簧用来模拟节点剪切变形。然而，上述模型考虑因素不全面，难以准确模拟梁柱节点的非线性反应。Fleury等[4]提出采用细长四边形网格模拟纵筋黏结滑移，通过2个相互平行的四结点单元模拟核心区混凝土和箍筋，采用多层混凝土梁过渡单元模拟节点两侧的梁端塑性铰区。该模型虽考虑因素全面，但建模过程计算量过大、效率较低、精确度不高。对此，Lowes等[5-6]提出了“超级节点”单元模型，该模型考虑因素全面、力学模型合理、计算量适中，已被纳入OpenSEES结构分析平台，称为梁柱节点单元(beam-column joint element，BCJE)模型。赵雯桐等[7]研究证明BCJE模型可较好的模拟钢筋混凝土梁柱节点的抗震分析。与普通混凝土相比，钢纤维混凝土开裂之后受拉应力应变曲线的峰值应力和应变明显提高，曲线下降段渐趋抬高和平缓，其对抗震性能的影响有明显不同。因此，BCJE模型用于SFRC梁柱节点抗震性能分析的数值模拟方法需进一步研究。

本文基于OpenSEES结构分析平台，首先分析了BCJE模型用于SFRC梁柱节点数值模拟的适用性，之后通过改进模型中钢筋滑移分量和剪切块分量的参数计算方法，提出了SFRC梁柱节点抗震性能分析的数值模型，并通过模拟相关文献中的6个梁柱节点试件，验证了其准确性。在此基础上，扩展分析了钢纤维体积率、配箍率和轴压比对梁柱节点抗震性能的影响规律，建立了SFRC梁柱节点受剪承载力计算公式。

1 BCJE模型适用性分析

BCJE模型为图1所示的由8个零长度钢筋滑移弹簧代替8个钢筋滑移分量、由4个零长度交界面剪切弹簧代替4个交界面剪切分量、1个剪切块分量组成的8个钢筋滑移分量、4个交界面剪切分量、1个剪切块分量组成[8]。

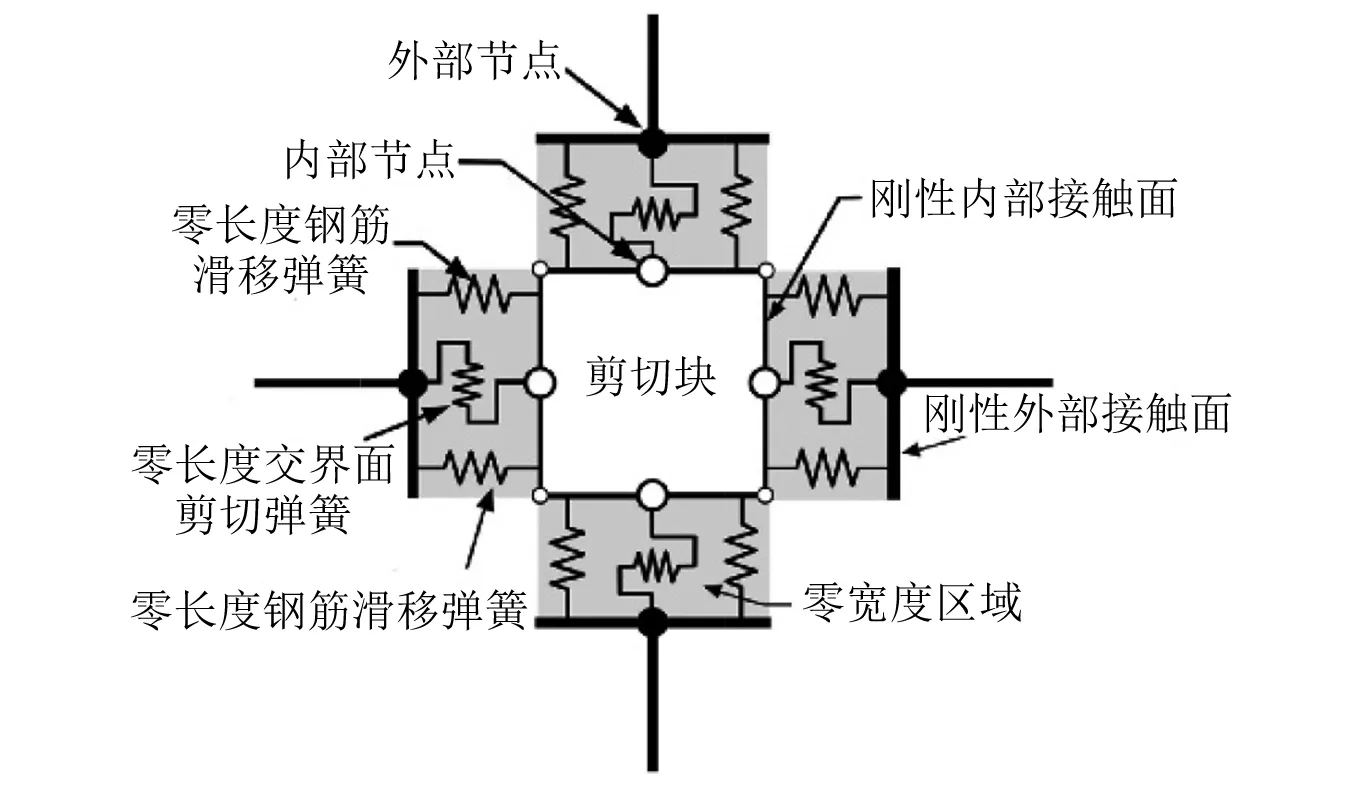
图1 BCJE模型Fig.1 Beam-column joint element model

利用该模型对文献中具有代表性的SFRC梁柱节点试件BCJ1-0、FRCJ1进行数值模拟，试件详细参数见文献[9-10]。建立有限元模型时，梁和柱采用非线性梁柱单元模型，其截面采用纤维截面；梁柱节点采用BCJE模型(模型中特征参数的取值按照模型开发者Mitra建议的方法确定)；钢筋采用Steel02本构模型[11]，钢纤维混凝土采用Concrete02本构模型[12]。模拟得到的滞回曲线与试验结果对比，如图2所示，关键特征点对比，见表1。

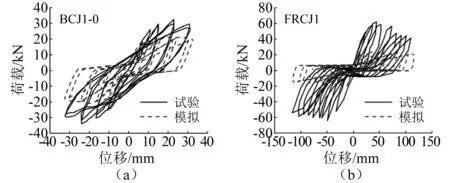
图2 滞回曲线对比图Fig.2 Comparison of hysteresis curve

表1 关键点的试验值与模拟值对比Tab.1 Comparison between test value and simulation value of key points

由对比结果可知，模拟得到的滞回曲线与试验结果相差较大，滞回环过于捏缩，耗能偏小，屈服荷载和峰值荷载均显著小于试验结果，说明BCJE模型模拟SFRC梁柱节点存在明显偏差。这主要是由于BCJE模型的分量参数是根据Mitra基于普通钢筋混凝土梁柱节点试验结果提出的计算方法确定的。其中，剪切块分量和梁纵筋黏结滑移分量是影响结果的关键参数。一方面，Mitra在确定剪切块分量特征参数时，是基于如图3所示的斜压杆模型，采用Mander等[13]约束普通混凝土本构，并考虑开裂后核心区混凝土有效压应力的软化得到的，而研究发现掺入钢纤维明显改变了核心区斜压杆混凝土的受力性能；另一方面，Mitra采用Barslip材料模型模拟梁纵筋黏结滑移弹簧参数，该模型是根据钢筋与普通混凝土拉拔试验确定的，没有考虑钢纤维对混凝土黏结性能的提高。因此，必须考虑钢纤维的影响，对BCJE模型中剪切块参数和梁筋黏结滑移参数的确定方法进行修正。

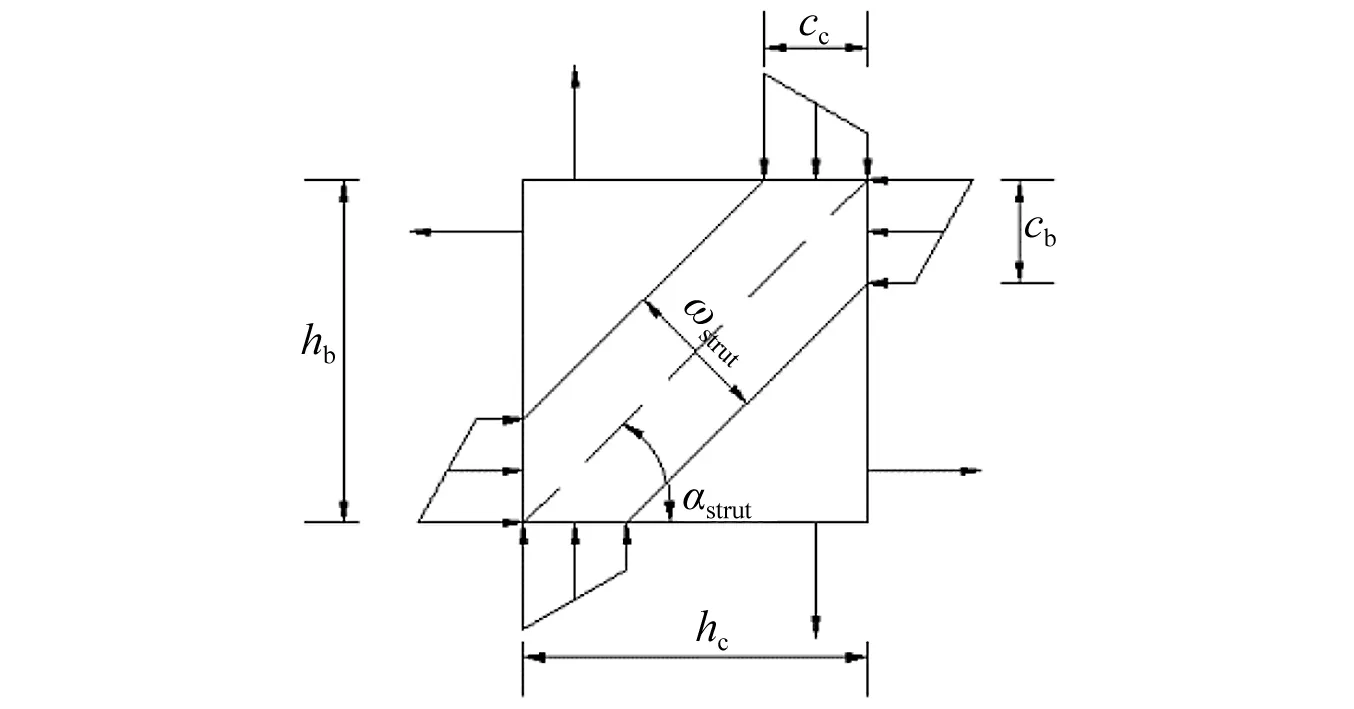
图3 斜压杆模型Fig.3 The diagonal compression strut model

2 BCJE模型改进

2.1 剪切块参数计算

研究发现，相较于单调加载，斜压杆在拉压往复荷载作用下存在软化现象，承载力有明显降低。因此，低周反复加载下钢纤维混凝土斜压杆的压应力fc,1可表示为

fc,1=αfc,0

(1)

式中：fc,0为单调加载下钢纤维混凝土斜压杆的压应力；α为钢纤维混凝土抗压强度折减系数。

选取史科研究中10个钢纤维混凝土梁柱节点，根据试验实测结果，通过式(2)计算其实测的核心区斜压杆压应力，即fc,1

(2)

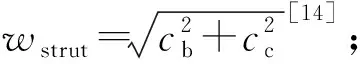
假定节点核心区剪切块发生变形时处于纯剪状态，可推导出斜压杆压应变εstrut与剪切块的剪切变形γ之间的关系，此外，根据材料力学可知，当剪切块处于纯剪状态时，其斜压杆压应变εstrut与主拉应变εt相等，因此，εt与γ之间的关系可表示为

εt=εstrut=γcosαstrutsinαstrut

(3)

图4中给出了根据10个钢纤维混凝土梁柱节点试验实测的剪切变形结果得到的钢纤维混凝土强度折减系数α与εt/ε0之间的关系，其中，α采用式(1)计算，fc,0是根据Mabsur等[15]提出的钢纤维混凝土单调受压本构关系计算出的压应力;ε0是根据Mabsur等本构模型计算出的极限抗压强度对应的压应变，εt则根据试验实测的节点剪应变γ按照式(3)进行计算。

图4 钢纤维混凝土抗压强度折减Fig.4 The reduction equation of the steel fiber concrete compressive strength

由图4可知，随着拉应变增大，折减系数α逐渐减小，当εt=0.79ε0时，α趋于平稳。通过回归分析，α可表示为

(4)

根据如图3所示的节点核心区斜压杆模型，可得剪切块分量的剪应力τ为式(5)

(5)

利用MATLAB程序，根据式(3)～式(5)，可计算出钢纤维混凝土梁柱节点模型中剪切块的特征参数和剪应力-剪应变骨架曲线，结果如图5所示。

图5 剪应变-剪应力骨架曲线Fig.5 Skeleton curve of shear stress-strain

2.2 梁纵筋黏结滑移分量参数确定

考虑钢纤维的掺入对混凝土黏结强度的提高，在改进后的BCJE模型中，梁纵筋黏结滑移分量采用Bond_SP01材料模型[16]模拟，其钢筋应力-滑移关系曲线如图6所示。图6中：Fy和Fu分别为钢筋的屈服强度和极限强度；Sy为钢筋达到屈服应力时的钢筋滑移值；Su为钢筋达极限强度时的钢筋位移值。

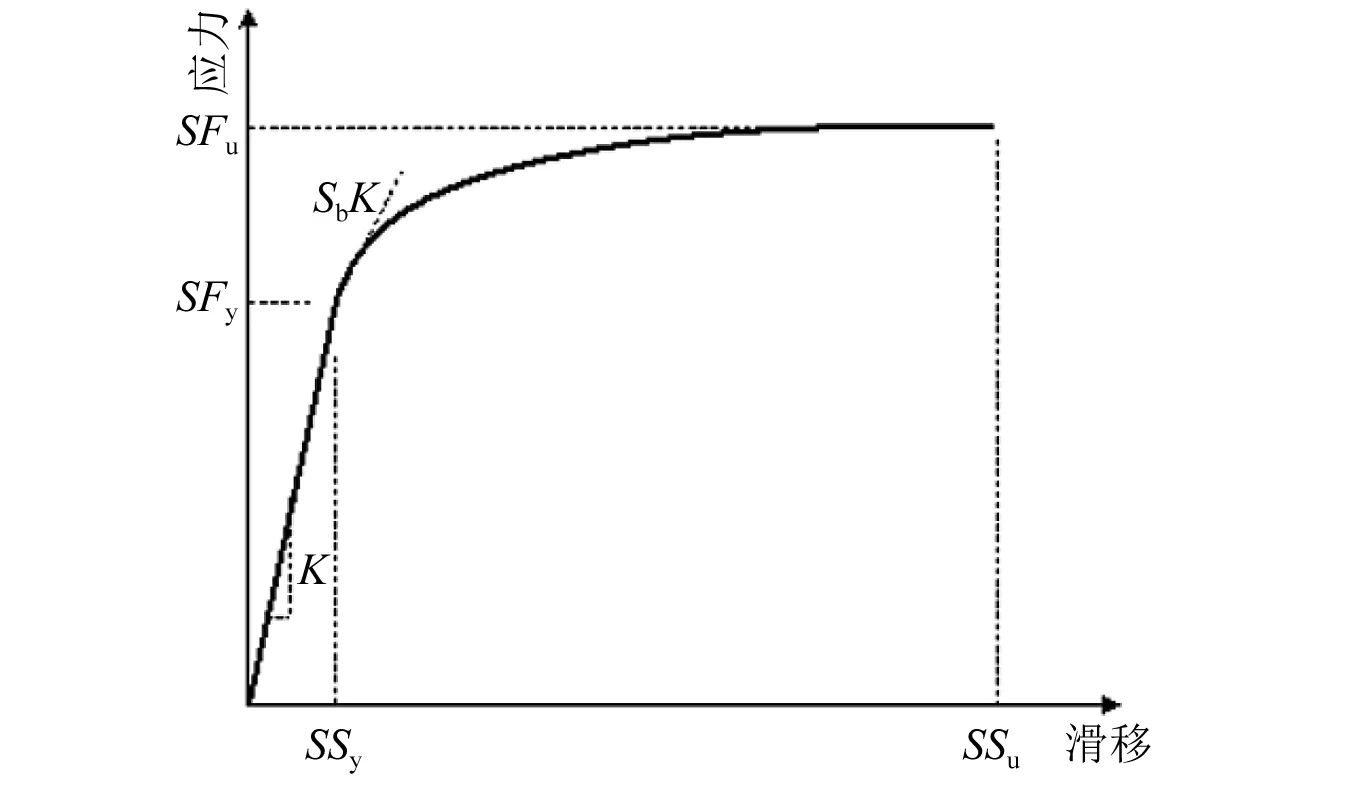
图6 Bond_SP01模型钢筋应力-滑移包络曲线Fig.6 Monotonic bar stress and slip response in Bond_SP01 material model

图6中，Sy和Su是根据OpenSEES用户手册推荐的公式计算得到的式(6)和式(7)[17]

(6)

Su=35Sy

(7)

式中，θ为描述局部黏结滑移关系的系数取值0.4。

而对于钢纤维混凝土，由于钢纤维的掺入能够提高混凝土的黏结强度，因此需要对式(6)中Sy的计算方法进行修正，本文Sy的修正是根据Harajli[18]推荐的公式进行的

Sy=S1e1.8[(uy/um,SFRC)2-1)]

(8)

(9)

(10)

(11)

式中：S1=0.15c0，c0为纵向受力钢筋净距；uy为屈服黏结应力；um,SFRC为最大黏结应力；c为最小混凝土保护层厚度；fc为混凝土抗压强度；Vf为钢纤维体积率；Lf/Df为钢纤维长径比；db为纵向钢筋直径。

3 改进后BCJE模型的验证

通过OpenSEES平台对修正后的BCJE模型进行验证，本文从史科和梁兴文等的研究中选取6个典型的SFRC梁柱节点试件，试件的主要参数如表2所示。

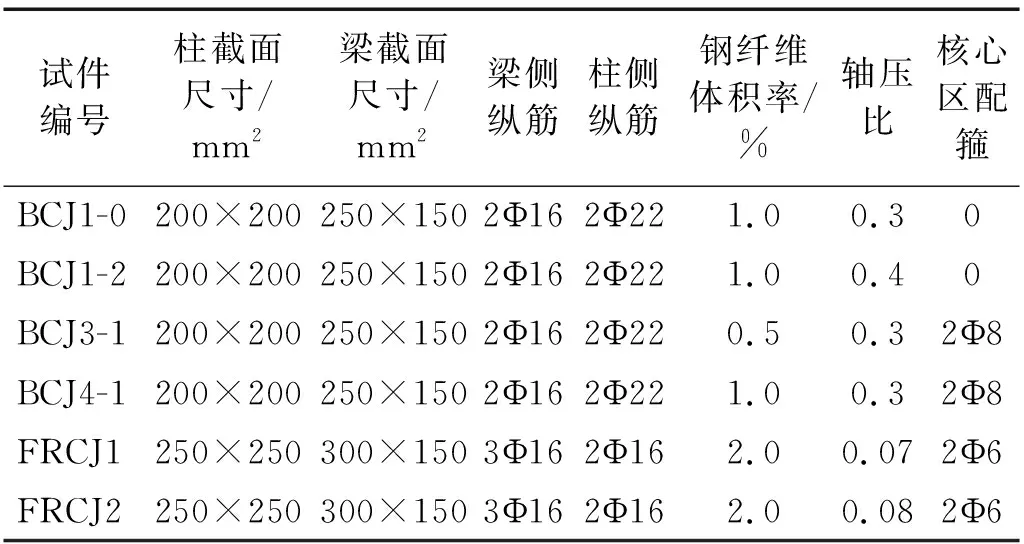
表2 SFRC梁柱节点试件试验参数Tab.2 Test parameters of steel fiber concrete beam-column joints

在OpenSEES软件中，采用前文提出的改进BCJE模型对上述6个试件进行模拟，改进BCJE模型中的剪切块分量的参数由式(3)～式(5)确定；梁纵筋黏结滑移分量的参数根据式(8)～式(11)确定。有限元模拟与试验实测的加载端荷载-位移滞回曲线和骨架曲线对比，如图7、图8所示，其骨架曲线的关键特征点对比见表3；由图7和图8可见，有限元模拟与试验结果吻合较好，随着位移荷载增大，试件刚度和承载力出现明显退化，并且有明显的滑移捏缩效应，整体趋势和试验基本相同，说明建立的模型可较准确的模拟梁柱节点在低周反复荷载作用下的滞回特性。根据骨架曲线可确定屈服位移、屈服荷载、极限位移和极限荷载，并计算其试验结果和模拟结果的比值，得到平均值和离散系数，如表3所示，各项指标的离散系数皆小于0.1，表明模拟具有较好的精度。节点荷载-剪应变滞回曲线对比如图9所示(由于史科仅给出的是各试件实测的荷载-剪应变滞回曲线，可模拟对比部分试件，因此，本文仅针对试验与模拟得到的荷载-剪应变滞回曲线)。由图9可知，4个试件的模拟误差均较小，且模拟可到荷载-剪应变滞回曲线的峰值荷载和最大剪应变，计算其试验结果和模拟结果的比值，得到的离散系数均小于0.1，详情如表4所示。

图7 滞回曲线对比图Fig.7 Comparison of hysteresis curve

图8 骨架曲线对比图Fig.8 Comparison of skeleton curve

表3 骨架曲线特征点对比Tab.3 Comparison of main feature points of skeleton curve

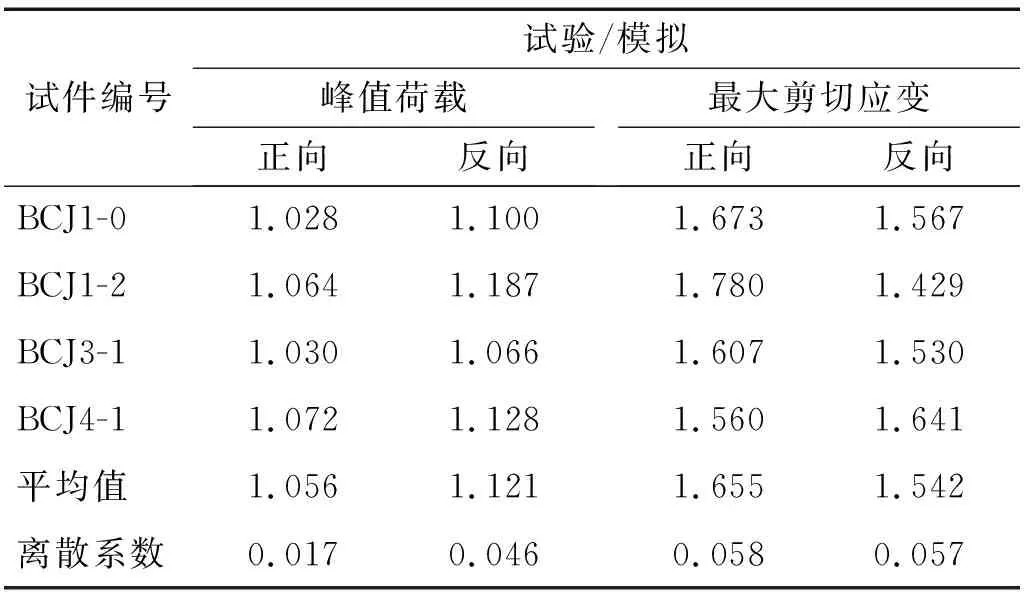
表4 荷载-剪应变特征点对比Tab.4 Comparison of main feature points load-shear strain

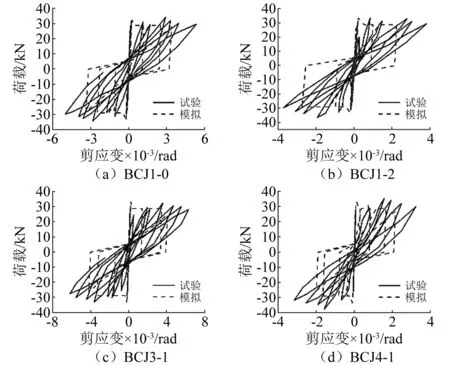
图9 荷载-剪应变对比图Fig.9 Comparison of load-shear strain

综上可知，本文提出的改进BCJE模型能够较准确地模拟SFRC梁柱节点的整体反应以及局部非弹性变形反应。

4 SFRC梁柱节点的参数扩展分析

根据上述建立的模型，分别研究钢纤维体积率、配箍率和轴压比对SFRC梁柱节点抗震性能的影响。试件为梁柱中节点：尺寸为柱端200 mm×200 mm，梁端250 mm×150 mm；试件配筋为梁端上下纵筋各2Φ16，柱端纵筋4Φ22；加载方式和制度同史科的研究。

4.1 钢纤维体积率

为研究钢纤维体积率的影响，设定钢纤维体积率变化为0.5%，1.0%，1.5%和2%，轴压比均为0.3，节点核心区均配置2Φ8。模拟得到的不同钢纤维体积率下梁柱节点骨架曲线和刚度退化曲线，如图10所示。由图10可以看出，钢纤维可显著改善梁柱节点的抗震性能，随着钢纤维体积率增加，节点承载力和延性提高，刚度退化减缓，钢纤维体积率从0.5%增加到2.0%时，极限荷载提高18%。

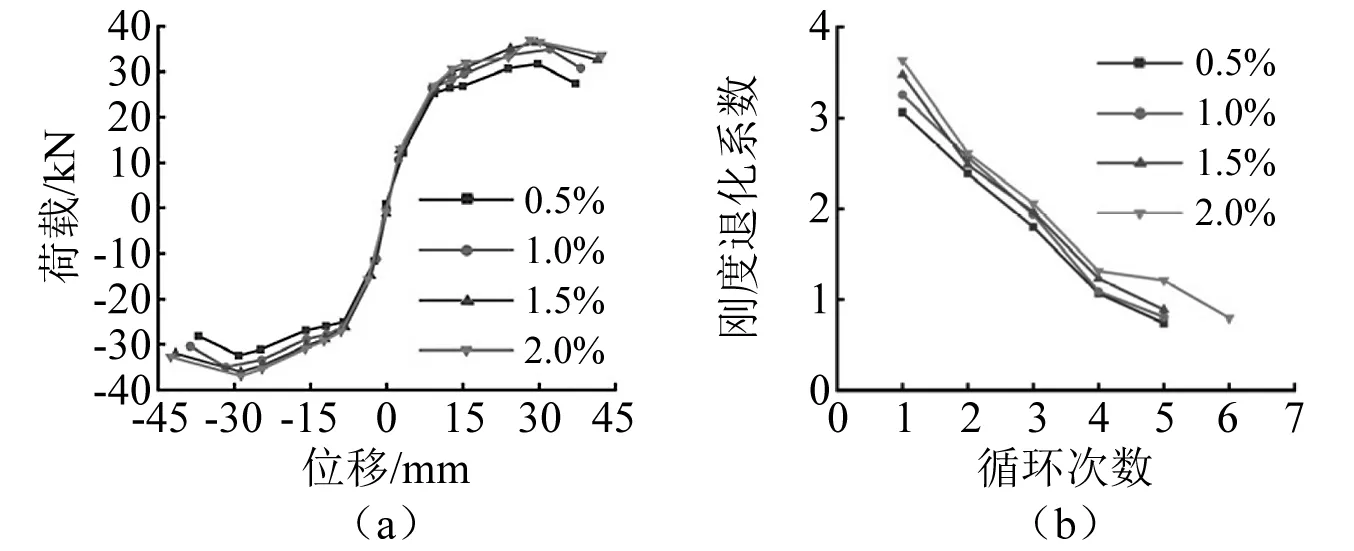
图10 不同钢纤维体积率下的骨架曲线和刚度退化曲线Fig.10 Skeleton curve and stiffness degradation curve under different steel fiber volumeratios

4.2 轴压比

为研究轴压比的影响，设定轴压比变化为0.2，0.3，0.4，0.5，钢纤维体积率均为1.0%，核心区配箍均为2Φ8。模拟得到的不同钢纤维体积率下梁柱节点骨架曲线和刚度退化曲线，如图11所示。由图11可以看出，轴压比从0.2增加到0.5时，极限荷载提高7.6%。

图11 不同轴压比下的骨架曲线和刚度退化曲线Fig.11 Skeleton curve and stiffness degradation curve under different axial compression ratios

4.3 核心区箍筋率

研究核心区箍筋的影响，设定节点核心区箍筋变化为1Φ8，2Φ8，3Φ8，钢纤维体积率为1.0%，轴压比均为0.3。模拟得到的不同核心区配箍率下梁柱节点骨架曲线和刚度退化曲线，如图12所示。由图12可以看出，增加箍筋可明显提高梁柱节点的抗震性能，当核心区箍筋从1Φ8增加到3Φ8时，极限荷载提高了19.7%。

图12 不同核心区配箍下的骨架曲线和刚度退化曲线Fig.12 Skeleton curve and stiffness degradation curve under different core areas with hoops

5 承载力计算公式

由上述分析可知，钢纤维体积率、核心区配箍和轴压比是影响SFRC梁柱节点受剪承载力Vj的主要因素，Vj可表示为

Vj=Vcf+Vs

(12)

式中：Vcf为节点核心区钢纤维混凝土受剪承载力；Vs为节点核心区箍筋受剪承载力。

基于斜压杆模型，参考文献[19]，Vcf的计算式为

Vcf=(α1+α2n)(1+α3vf)fchjbj

(13)

式中：n为柱端轴压比；α1，α2，α3为影响系数；hj，bj分别为截面高度和宽度。

参考GB 50010—2010《混凝土结构设计规范》[20]，并考虑节点核心区箍筋受力不均匀的影响，Vs的计算式为

(14)

式中：fyv为箍筋抗拉强度；Ayv，s分别为箍筋截面面积和间距；h0为节点核心区有效高度；a′s为纵向钢筋合力点到混凝土边缘距离。

将式(13)和式(14)代入式(12)，可得

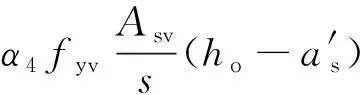
(15)

利用建立的数值模型，针对上文建立的梁柱节点试件，分别求得节点核心区钢纤维体积率为0.5%，1.0%，对应的配箍分别为0，1Φ8，2Φ8，3Φ8，4Φ8，5Φ8时，梁柱节点的受剪承载力。根据模拟结果对式(15)进行回归分析可得：α1=0.366 1，α2=-1.112 9，α3=7.271 8，α4=0.112 4。图13为数值模拟与计算结果的对比，可知吻合较好。

图13 承载力模拟与拟合结果对比Fig.13 Comparison of bearing capacity simulation results and fitting results

6 结 论

本文结合SFRC的受力特征，通过改进了BCJE模型中钢筋滑移分量和剪切块分量的参数确定方法，提出了修正BCJE模型，将模拟结果与试验结果进行对比，同时分析了钢纤维体积率、轴压比的影响，建立了受剪承载力计算公式，得出以下结论：

(1) OpenSEES中的BCJE模型不适用于SFRC梁柱节点试件的受力特征分析，其模拟结果存在明显误差。

(2) 针对SFRC梁柱节点提出的修正BCJE模型能够较好的模拟SFRC梁柱节点在低周反复荷载作用下的滞回特征，同时能够较好反映节点核心区剪应力和剪应变发展变化的全过程。

(3) 掺入钢纤维和增加配箍可明显改善钢筋钢纤维混凝土梁柱节点的抗震性能，轴压比影响相对较小。随钢纤维体积率和配箍量的增加，极限荷载和延性都有显著提高，骨架曲线下降段减缓。

(4) 提出的受剪承载力计算公式可反映钢纤维和箍筋的影响，与数值模拟结果吻合较好。