单自由度碰撞振动系统的奇异非混沌动力学和多稳态共存

吴 鑫， 李高磊， 乐 源

(西南交通大学 力学与工程学院，成都 610031)

具有悬臂结构的碰撞系统作为一类典型的非光滑系统，已广泛应用于航空航天、机械制造、电子器件等工业领域[1-3]。通常，非光滑系统中的非光滑因素来源于系统间隙、碰撞或干摩擦等。而具有悬臂结构的碰撞振动系统则同时具有悬臂结构弯曲产生的几何非线性因素和碰撞所产生的非光滑因素，其累积效应通常会使系统产生更加复杂的动力学现象[4]。目前，对悬臂碰撞振动系统的研究主要集中在系统的谐波共振、分岔和混沌等动力学行为方面[5-7]。目前尚无关于悬臂碰撞振动系统的奇异非混沌动力学方面的相关研究。

奇异非混沌吸引子(strange nonchaotic attractors, SNAs)是奇异但非混沌的吸引集，其通常产生于拟周期运动与混沌运动之间。“奇异”指的是吸引子具有分形的几何结构。“非混沌”指的是吸引子不依赖于系统的初始条件，即最大Lyapunov指数为非正数。从Grebogi等[8]在1984年首次揭示SNAs以来，人们认识到“奇异”并非等价于“混沌”，并在各类非线性动力系统中通过理论、数值和试验等方法对SNAs进行了广泛的研究。目前奇异非混沌动力学已经成为动力学领域重要的研究课题之一。

Ding等[9]从数值和解析的角度证实了SNAs在拟周期系统中的存在，并举例说明了在典型的拟周期系统中可能出现的多种动力学行为。Pikovsky等[10]利用SNAs对外激励相位具有敏感依赖性，通过计算相敏感指数来刻画吸引子的奇异性。Nishikawa等[11]利用不变曲线的泛函方程研究了一类SNAs在拟周期激励系统中的分形及混沌演化。Witt等[12]通过研究受拟周期激励Logistic映射的周期3窗口的内部激变，发现了由内部激变导致SNAs产生的新机制。Ditto等[13]在研究受双频拟周期激励的屈曲磁弹性带的试验中，首次证实了SNAs的存在。Thamilmaran等[14]通过试验方法在LCR电路系统发现了产生SNAs的三种路径，即Heagy-Hammel路径、分形路径和阵发路径。Chithra等[15]在三阶混沌电路系统中发现了混沌吸引子及奇异非混沌吸引子，并通过最大Lyapunov指数、功率谱和0-1测试方法对两种吸引子进行了区分。Lindner等[16]利用开普勒太空望远镜记录了天琴座内一些恒星的亮度在主频率和次频率上波动的光线曲线，这两种频率的比率接近于黄金分割值，而由次频率驱动的非线性动力系统通常存在SNAs，这是实验室外首次证实SNAs的存在。

上面的研究对象多数是针对光滑系统。目前已经有研究发现在碰撞类非光滑系统中也存在丰富的奇异非混沌动力学现象。Zhang等[17]研究了一类刚性约束碰撞振动系统在余维三分岔点附近由于环面倍化中断而产生的SNAs。Yue等[18]通过研究周期激励的三自由度对称碰撞振动模型，在系统余维二分岔点附近发现存在SNAs，并进一步讨论了SNAs与混沌吸引子等的共存情况。

在实际工程中，具有悬臂结构的碰撞振动系统有时处于复杂的外部环境中。通常，可用多频激励来近似模拟系统在外荷载作用下的振动碰撞，当各激振频率不可有理通约时，则可以视为系统受拟周期激励[19]。本文在以上研究基础上，建立一类受拟周期激励的具有悬臂结构的碰撞振动非光滑模型，揭示了其奇异非混沌动力学以及多稳态共存现象。通过相敏感性、奇异连续谱和有理数频率逼近以及状态变量的傅里叶变换的部分和在复平面上的路径等工具刻画了吸引子的奇异性；并利用最大Lyapunov指数[20-22]描述了吸引子的非混沌性。研究发现此类非光滑系统中SNAs的两种不同演化路径及其与拟周期吸引子及混沌吸引子共存的多稳态现象。

1 含悬臂结构碰撞振动系统的动力学模型

含悬臂结构碰撞振动系统的动力学模型，如图1所示。质量为M的质量块连接在两根悬臂结构的自由端，悬臂结构简化为两片板式弹簧，不计质量，长度为L，抗弯刚度为EI(E，I分别为悬臂结构的弹性模量和截面惯性矩)。质量块受到F1=A1cos(ωt)和F2=A2cos(φt)的激励力作用，e1和e2为质量块与弹簧约束面之间的间隙。以系统静止时质量块上边缘为坐标原点，竖直向下为正方向，建立直角坐标系。当质量块的位移为e1或-e2时，将会与上下两个弹性约束面发生碰撞。

图1 含悬臂结构碰撞振动系统的动力学模型Fig.1 Dynamic model of vibro-impact system with cantilever

单自由度含悬臂结构碰撞振动系统的的运动微分方程为

(1)

式中：f(X)为悬臂结构的弹性恢复力，其可以描述为非线性形式

(2)

E(X)为间隙分段函数，其表达式为

(3)

引入无量纲量，式(1)可转化为

(4)

其中，

(5)

令θ=ωt，φ=φt，将式(4)在相空间R2×T2中写成如下形式

(6)

通过角度变量φ引入三维Poincaré映射

Π:Σ→Σ,
Σ≡{(x,v,θ)∈R×R×S1|φmod 2π=0}

(7)

则映射方程可表示为

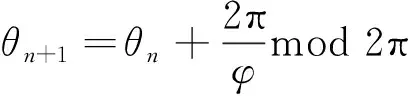
(8)

2 吸引子奇异性验证

2.1 相敏感函数

由于映射式(8)在区间θ=[0 2π]上稠密，所以其SNAs是不分段可微的。SNAs对系统初始条件的改变不具有敏感性，这反映在其最大Lyapnuov指数为非正数。然而，其对外激励的相位却具有敏感依赖性。基于此可以通过研究吸引子对相位的导数来刻画吸引子的奇异性。吸引子对相位的导数为

(9)

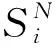
相敏感函数可以通过计算SNAs的时间序列而获得。对于任意小的ε，存在于满足相位差ε0=|θn0-θ0|<ε的n0，则吸引子对相位的导数又可近似表示为

(10)

(11)

2.2 奇异连续谱

奇异连续谱法是在研究拟周期晶格模型和受拟周期激励的量子系统中首次提出。通常，动力系统的功率谱具有三种状态：周期或拟周期等常规运动对应的离散功率谱、混沌或随机运动对应的连续功率谱、奇异非混沌运动对应的奇异连续谱。因此，通过对吸引子进行谱分析可以验证吸引子的奇异性。

系统状态变量x的傅里叶变换部分和可表示为[23]

(12)

式中：Ω与系统两个激励力的频率之比成比例关系； 当T为时间时，X(Ω,T)为复平面上(ReX,ImX)上的路径。通常，X(Ω,T)与T存在以下幂率关系

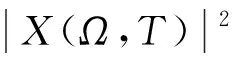
(13)

式中，ρ为标度因子。若系统吸引子为SNAs，则1<ρ<2，且X(Ω,T)在复平面(ReX,ImX)上的路径具有分形自相似结构。

2.3 有理数频率逼近

φk=Fk-1/Fk，Fk=1,1,2,3,5,8,…

(14)

式中，Fk为斐波纳契数。则系统无理数频率可以表示为极限形式

(15)

通过以上变换，原拟周期系统转换为周期系统。

3 奇异非混沌吸引子

抗弯刚度作为悬臂结构的重要力学参数之一，对其深入研究具有重要理论及现实意义。对于本系统，当系统质量块质量和悬臂结构长度确定后，则无量纲参数α可视为系统悬臂结构的抗弯刚度系数。因此，对系统抗弯刚度的研究可转换为对系统参数α的研究。下面研究均以系统参数α为控制参数。

图2 α=0.620，1T环面Fig.2 For α=0.620，1T tours

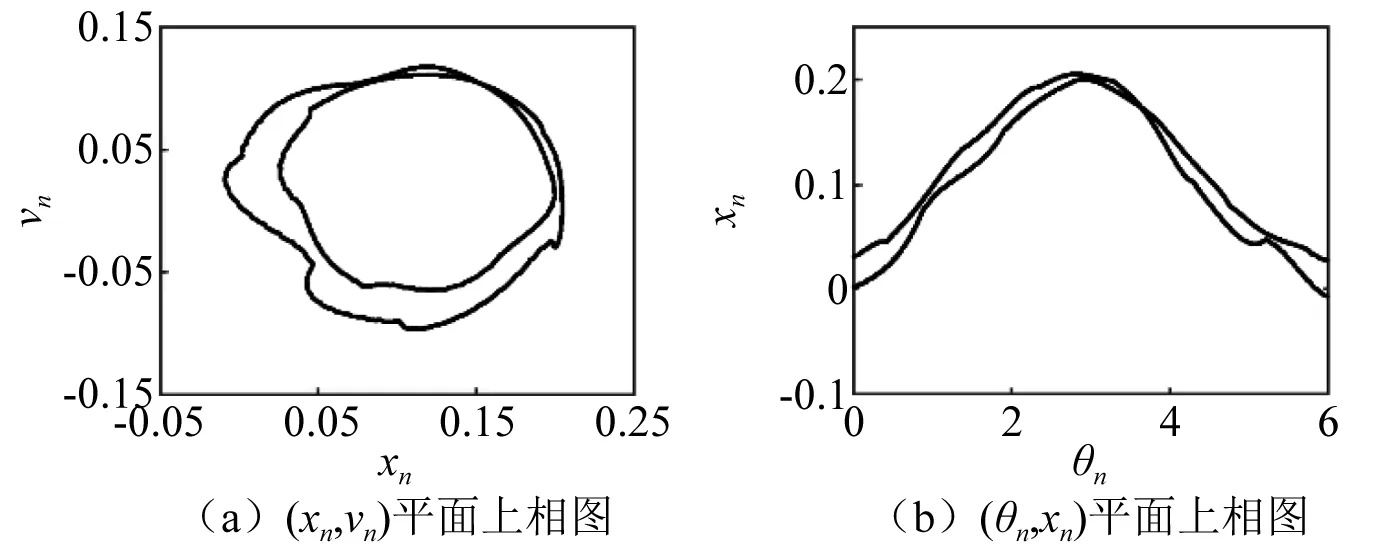
图3 α=0.610，2T环面Fig.3 For α=0.610，2T tours

图4 α=0.59，2T环面Fig.4 For α=0.59，2T tours

图5 α=0.587 7，SNAFig.5 For α=0.587 7，SNA

图6 α=0.56，混沌吸引子Fig.6 For α=0.56，chaotic attractor

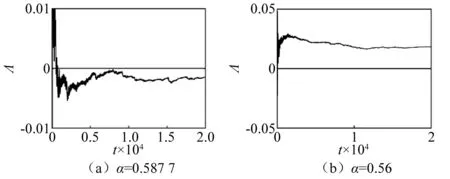
图7 最大Lyapunov指数谱Fig.7 Top Lyapunov exponent

图8 α=0.59, α=0.587 7时相敏感函数Fig.8 Phase sensitivity function when α=0.59, α=0.587 7

当α=0.587 7时系统的奇异连续谱，如图9(a)所示。由图9(a)可见，此时标度因子β=1.28；X(Ω,T)在复平面(ReX,ImX)上的路径图像，如图9(b)所示。可以看出其具有明显的分形结构，这也表明了吸引子的奇异性。

图9 α=0.587 7时的奇异连续谱和分形结构Fig.9 Singular continuous spectrum and fractal structure when α=0.587 7

图10为当近似阶数为φk=144/233，φk=6 765/10 946时近似系统在(θn,xn)平面上对应的相图，对比图5和图10可以看出，当近似阶数增加时，近似系统的吸引子进一步逼近原系统的吸引子，这再一次证实了α=0.587 7时系统吸引子的奇异。

图10 α=0.587 7时有理数频率逼近Fig.10 Rational frequency approximation when α=0.587 7

4 奇异非混沌吸引子的产生机制

4.1 分形路径

图11 α=0.615，1T环面Fig.11 For α=0.615，1T tours

图12 α=0.605，1T环面Fig.12 For α=0.605，1T tours

图13 α=0.600 5，SNAFig.13 For α=0.600 5，SNA

图14 α=0.605, α=0.600 5时相敏感函数Fig.14 Phase sensitivity function when α=0.605, α=0.600 5

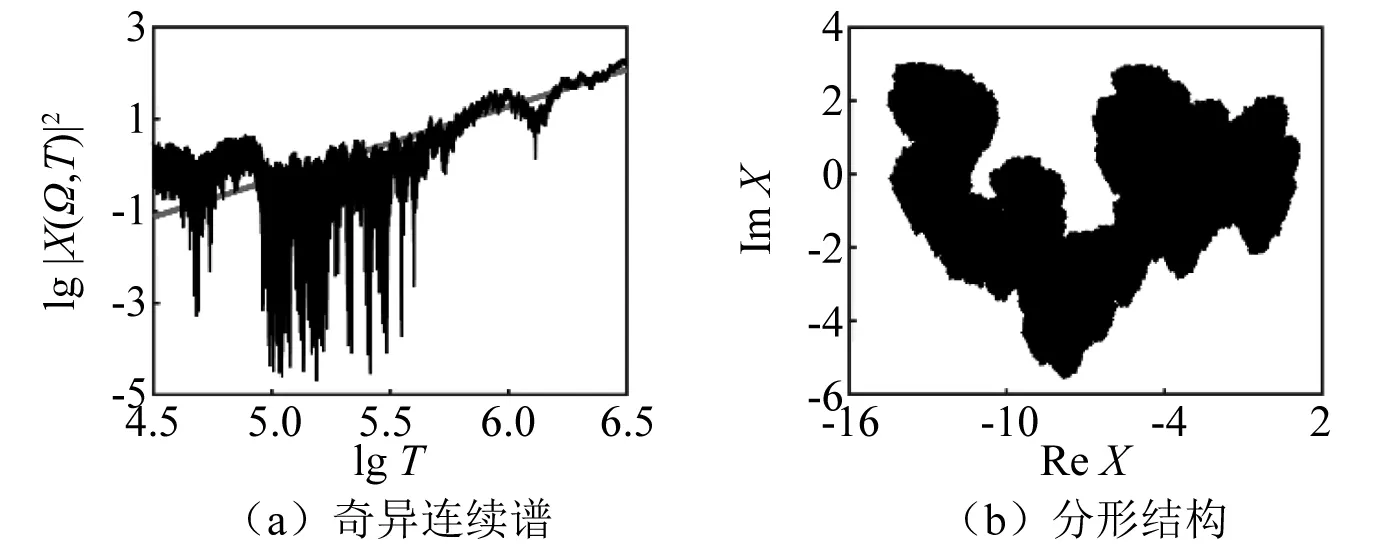
图15 α=0.600 5时的奇异连续谱和分形结构Fig.15 Singular continuous spectrum and fractal structure when α=0.600 5

图16 α=0.600 5时的有理数频率逼近和最大Lyapunov指数谱图16 Rational frequency approximation and top Lyapunov exponent when α=0.600 5

4.2 阵发路径

图17 α=0.59，1T环面Fig.17 For α=0.59，1T tours

图18 α=0.587，SNAFig.18 For α=0.587，SNA

SNAs的奇异性同样通过相敏感性、奇异连续谱和有理数频率逼近的方法进行刻画。通过系统相敏感函数描述系统在此参数条件下吸引子的奇异性，如图19所示。图20(a)为α=0.587时吸引子的奇异连续谱，可以看出SNA的奇异连续谱呈现出很强的幂率行为，此ρ=1.50，同时X(Ω,T)在复平面(ReX,ImX)上的路径也具有明显分形特征，如图20(b)所示。图21(a)为取近似阶数φ6 765=6 765/10 946的有理数逼近，其与图18(b)中的结构相似。

图19 α=0.587时相敏感函数Fig.19 Phase sensitivity function when α=0.587

图20 α=0.587时奇异连续谱和分形结构Fig.20 Singular continuous spectrum and fractal structure when α=0.587

在图21(b)中，系统最大Lyapunov指数收敛于负值，表明了此时吸引子的非混沌性。

图21 α=0.587时有理数频率逼近和最大Lyapunov指数谱Fig.21 Rational frequency approximation and top Lyapunov exponent when α=0.587

5 奇异非混沌吸引子的多稳态动力学

图22 (θn,xn)平面上相图Fig.22 Phase diagrams in (θn,xn)

当α进一步减小到0.608 27时，系统的稳态SNA演化为暂态SNA。由图23(a)可见，当初始条件为(0.15,0.15)时，系统随时间的演化由奇异非混沌运动转变为拟周期运动，图23(b)为初始条件为(0,0)时系统状态变量v的时间序列。不同时间区域内系统在(θn,xn)上的相图，如图24所示。由图24(a)可见，在[0,30 000]时间区域内，系统T-SNA与2T拟周期吸引子共存。

图23 α=0.608 27状态变量v的时间序列Fig.23 Time series of the state variable v when α=0.608 27

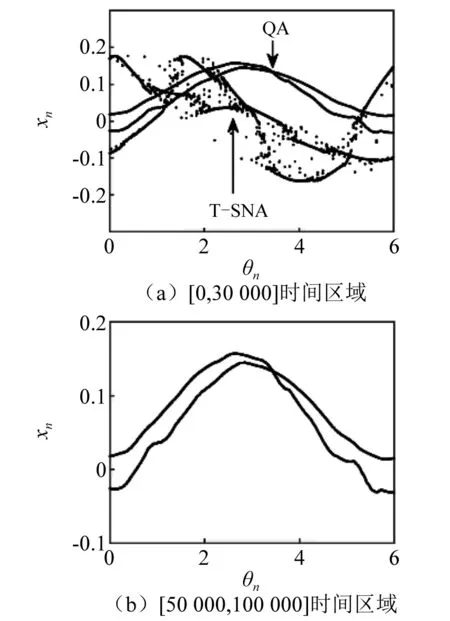
图24 α=0.608 27时(θn,xn)平面上相图Fig.24 For α=0.608 27, phase diagrams in (θn,xn)

当α=0.599时，系统由暂态SNA演化为暂态混沌，如图25(a)所示，同样地，图25(b)为初始条件为(0,0)时，系统状态变量v的时间序列。图26(a)展示了系统在[0,30 000]时间区域内SNA与暂态混沌的共存情况。图26(b)为系统在[50 000,100 000]时间区域内的相图，此时系统暂态混沌吸引子已转变为SNA。通过图27系统最大Lyapunov指数发现，随着时间不断演化，最大Lyapunov指数由正值进入负值，这也表明了系统的暂态混沌发生转移。

图25 α=0.599状态变量v的时间序列Fig.25 Time series of the state variable v when α=0.599

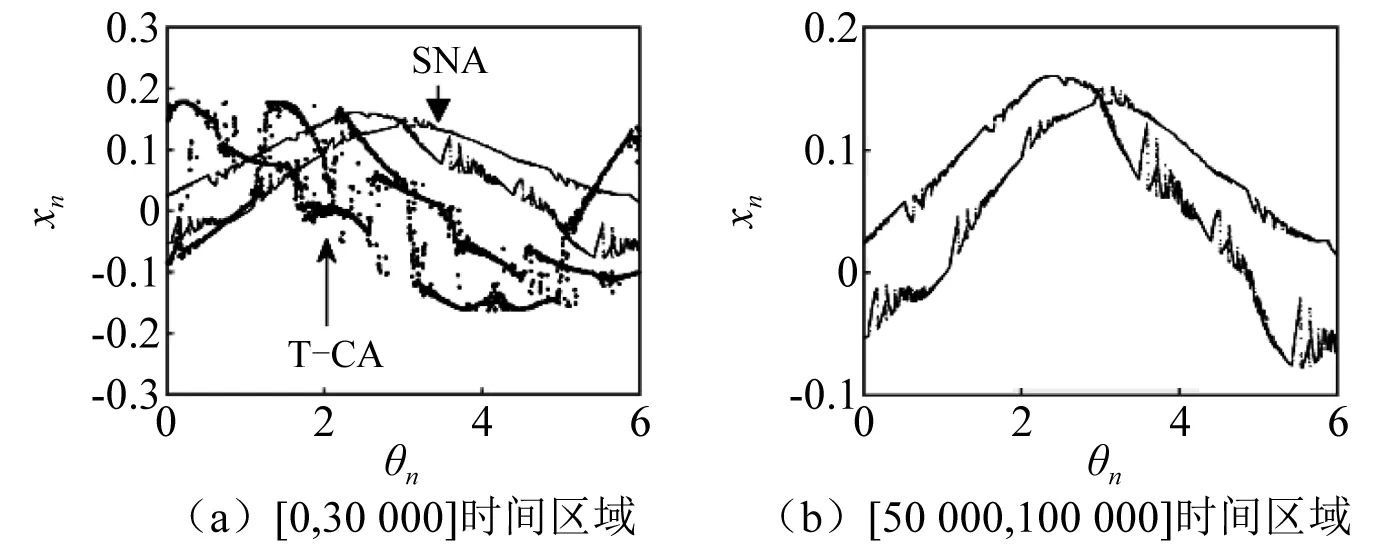
图26 α=0.599时(θn,xn)平面上相图Fig.26 For α=0.599, phase diagrams in (θn,xn)

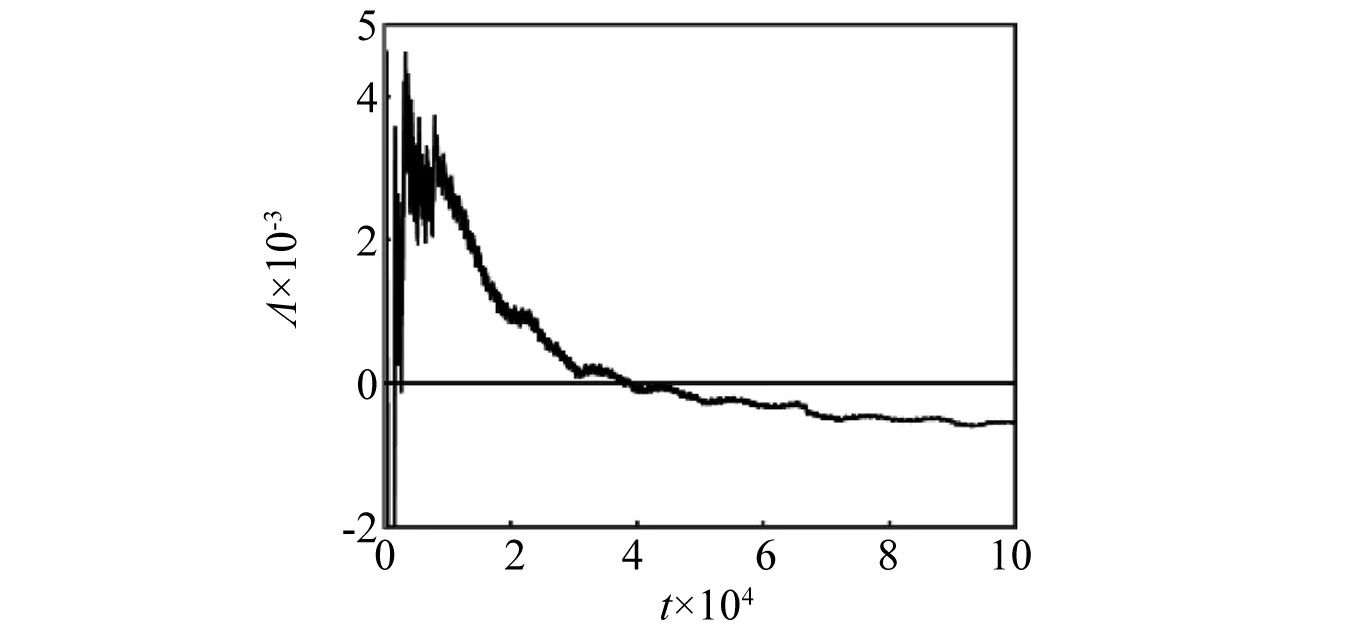
图27 α=0.599， (x0,v0)=(0.15,0.15)时最大Lyapunov指数谱Fig.27 For α=0.599, (x0,v0)=(0.15,0.15) top Lyapunov exponent

而当α最终减小到0.593时，系统此时仅存混沌运动，如图28所示，其对应的最大Lyapunov指数为0.004。

图28 α=0.593时(θn,xn)平面上相图Fig.28 For α=0.593, phase diagrams in (θn,xn)

6 结 论

奇异非混沌动力学的研究已经开展了三十多年，目前大多数的研究主要针对于不同领域的离散或光滑系统。本文以一类双频激励的具有悬臂结构的碰撞振动系统为研究对象，建立了系统的运动微分方程。利用相敏感函数、奇异连续谱、有理数频率逼近、状态变量的傅里叶变换的部分和在复平面上的路径、最大Lyapunov指数等工具，揭示了悬臂碰撞振动系统丰富而又复杂的奇异非混沌动力学及其多稳态现象。研究结果表明：

(1) 通常拟周期运动通过无限次的倍化可直接通向混沌。而本系统1T环面经过一次倍化而变成2T环面后，拟周期吸引子便产生扭曲和褶皱，从而导致倍化终止。随着参数变化，拟周期吸引子首先演化为SNA，最后通向混沌。

(2) 在某些参数区间，系统存在通向SNAs的不同路径，即分形路径和阵发路径。分形路径的显著特征是拟周期吸引子产生褶皱状，这也可视为SNAs出现的前兆，而阵发路径的特征是原拟周期吸引子附近出现散乱无序的离散点，直到演变为SNAs。

(3) 系统存在暂态及稳态SNAs与拟周期吸引子的共存、稳态SNAs与混沌吸引子的共存情况，首先出现的SNA是由阵发路径而产生，且通过数值计算发现其共存区间较短。当稳态SNA转变为暂态SNA后，另一个拟周期吸引子也逐渐开始向SNA演化。当后面的拟周期吸引子演变为SNA时，系统暂态SNA也演化为暂态混沌吸引子，此时系统SNA与暂态混沌吸引子发生共存。最终，系统暂态混沌消失，SNA转迁为稳定的混沌吸引子。

本文的研究方法和结果可为非光滑连续系统中的奇异非混沌动力学理论研究提供思路，同时也可为工程中含悬臂结构的相关碰撞装置或构件的设计和优化提供理论支持。