周期性低频尾迹对边界层演变影响的瞬态研究

孙海鸥， 任翱宇， 王艳华， 王忠义， 曲永磊

(哈尔滨工程大学 动力与能源工程学院，黑龙江 哈尔滨 150001)

作为燃气轮机的主要部件之一，压气机总是在强逆压梯度条件下运行，这使得压气机叶片的运行环境恶劣。强逆压梯度导致了更大的压阻，加厚了叶片吸力面边界层，从而导致更严重的边界层分离和能量能量损失。

人们正详细地研究和理解强逆压梯度下的叶片表面流动机理。Pietro Zunino教授的团队利用一个简化的模型针对叶片表面的分离剪切层做了一系列的实验研究。Bernardini等[1]用一个平板模型取代叶片，在平板的上下空间加装内凹的挡板来制造逆压梯度。当转捩过程发生的时候，可以观察到分离和再附着现象形成一个具备一定厚度的边界层，称为层流分离泡。Simoni等[2-3]对关于来流尾迹与层流分离泡不稳定机理之间的交互作用进行了实验研究。将动叶尾缘简化为扰流棒，极大降低了实验的难度并使得关注重点落在尾迹对平板表面流动的影响上。该实验在热那亚大学的空气动力与涡轮机械实验室的一个开式低速风洞中进行，得到了关于大尺度涡结构的高清图像[4]。以上这些带有来流尾迹的研究工作得到了一些有意义的结论，比如粘性剪切层内速度波动得到了放大，且最大的波动会发生在分离边界层最厚的位置附近；分离泡会表现出周期性的厚度变化，包含来流尾迹对分离泡的抑制作用。

鉴于发动机叶型的多样性，针对平板进行研究易于得到表面流动分离的普适性的机理，但是目前通过对来流尾迹对平板表面分离流动影响的数值模拟来研究压气机叶片表面的边界层演变做的较少。一些针对无扰流棒的平板数值模拟可以作为研究参考，除了上文提到的，还有李华君等[5]针对平板转捩所做的详细分析。通过LES模型计算，他们的文章认为分离剪切层内的转捩过程是由流线型条纹和无粘Kelvin-Helmholtz不稳定性共同引起，前者占据了主要原因。该观点与主流认为的Kelvin-Helmholtz不稳定性是引起转捩的主要原因存在不同。张衡[6-7]对来流尾迹对涡轮叶片吸力面边界层的影响进行了数值模拟研究，得到了大量关于来流尾迹和涡轮叶片吸力面边界层厚度变化之间的定性分析。邓飞等[8]利用振动降低近壁流场的湍流度，结果近壁处更加趋近于层流。

本文使用与文献[1]中相同的物理模型作为研究对象，以方便数值方法的验证。尝试利用扰流棒与平板间的相互运动模式来代表压气机的级运动，聚焦于通过CFD方法揭示低频尾迹对平板吸力面分离剪切层的周期性影响机理。该研究有利于加深对压气机叶片在强逆压梯度下边界层演变的理解，同时，对低频尾迹与边界层相互作用机理的关注同样有助于为湍流运动机理分析提供可靠的参考。

1 数值方法与验证

1.1 模型结构

用于数值模拟方法验证的模型为图1中扰流棒的右侧部分，该未带扰流棒的部分从参考文献[1]提取，其关于平板表面边界层分离的实验研究在热那亚大学空气动力及涡轮机械实验室完成。平板全长300 mm，包括有效弦长L=200 mm和尾缘100 mm，前缘为8∶1的椭圆形且平板厚度19.4 mm。平板被安装在上下2块挡板之间形成缩放通道来制造逆压梯度环境。一个0.2 mm厚与1 mm宽的长方形薄片被粘贴在上端壁的喉道略靠后的位置，用来促进上部挡板表面的转捩过程，从而减少甚至消除上部挡板表面的边界层厚度对气流通道压力分布的影响。在数值模拟中直接设置上挡板表面壁面剪切力为0来起到相同作用。

图1 模型结构图及参数

在实验中，平板内外两侧靠近测试段壁面处的数据精确度不高，因此采用图3所示的平板纵向中截面来进行二维数值模拟。

1.2 数值模拟方法

在控制流动中，大尺度湍流和非稳定强迫扰动之间的相互作用是首要问题。为了获得与大尺度涡旋相关的可靠结果，本文使用Fluent软件中的压力基URANS模型来预测全局流场。由ICEM软件为模型提供完美的结构网格，包括30层极密的边界层网格，来确保平板表面包括边界层的厚度范围内的Y+值远远小于1。通过在其余位置进行合理的网格布局，得到了高质量的全局网格。文献[1]已经对2个不同的转捩模型，transition SST 和transitionk-kL-ω进行了比较，结果表明transitionk-kL-ω模型在更多的测试区域贴合实验结果，其预测性能优异。本文选择该模型作为预测流动转捩的数值模型，并基于the least squares cell进行空间离散，它在适用于多面网格方面与Green-gauss node-based 方法具有相同的精度。采用二阶方案来进行压力与动量的计算。

平板表面设置为无滑移壁面，上下挡板为滑移壁面，设置计算域压力进口与静压出口，其中入口边界条件湍流度为1.5%。对Re=70 000 和Re=200 000 这2种工况进行数值模拟。平板平直段长度L=200 mm为特征长度，由雷诺数换算得到质量流量作为流道压力差的目标流量，并在静压出口条件中设置。

1.3 数值验证

首先使用4套网格进行网格无关性的研究，使用平板上表面的平均表面摩擦系数Cf来评估收敛性能。图2展示了网格计算的比较结果。在网格加密至数量超过64万以后，平板表面的轴向Cf值几乎不再变化，因此64万这套网格为用作后续的数值模拟。

图2 Re=70 000时不同网格对应的Cf 值

在Re=70 000和Re=200 000这2种条件下针对压力系数Cp的CFD值与实验值之间的校核如图3所示。可以看出，数值模拟结果在绝大部分位置与实验值相符合。在Re=70 000时数值模型的预测性能要优于Re=200 000的情况。因此，URAN计算和transitionk-kL-ω转捩模型将作为本文后续数值研究的方法。

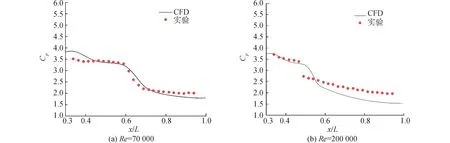
图3 平板表面压力系数分布

2 周期性来流条件设置

如图2所示，在验证模型的平板前端加入了垂直方向阵列布置的扰流棒。根据实验，扰流棒圆心与平板前缘最前端之间的水平距离为66.67 mm，即1/3L。设定扰流棒向上运动，则平板的上表面代表压气机静叶的吸力面。

扰流棒相关运动参数如下：折合频率系数f+如式(1)所示，

(1)

是扰流棒频率与轴向气流流动频率之间的比值，表征扰流棒运动与轴向气流流动之间的交互关系。式中：Ubar是扰流棒移动速度，Sbar是扰流棒间距，c1原代表动叶出口气流绝对速度，在平板流动研究中表示扰流棒区域前的轴向来流速度，Lchord是平板有效弦长200 mm。

速度比φ表示来流速度与扰流棒速度之间的相对关系，参考压气机中某级动叶转速与出口气流绝对速度，结合实验经验，选取φ值为2/3。

φ=c1/Ubar

(2)

鉴于在Re=70 000时的数值模拟结果具有更高的可靠性，选取该条件作为研究的来流参数，并据此确定来轴向来流速度c1。同时，设定f+=0.5，作为本文研究的低频尾迹频率。从而得到一系列边界条件：环境温度T=288.15K, 空气密度ρ=1.225 kg/m3, 空气动力粘度μ=1.789×10-5kg/(m·s), 进口轴向来流速度U0=4.992 m/s,Ubar= 7.488 m/s，扰流棒上移单周期为0.08 s，进口湍流强度为4%。扰流棒的向上平移通过网格移动来实现，扰流棒区域和前方来流区域，还有后方平板区域通过交界面连接。

自由流湍流度是流动分离的主要影响因素之一。Balzer等[9]的研究表明自由流湍流水平达到2.5%时在分离泡的上游出现流向条纹，转捩同时由流向条纹和K-H不稳定性驱动。Simoni[10]在2.87%的湍流强度下进行研究时，发现层流泡会在雷诺数增加到90 000时消失。Zaki[11]对压气机叶片气流分离的研究发现当自由流湍流度达到5.5%时，吸力面的分离完全消除，转捩由针对T-S不稳定性的绕过机制主导。通常，低湍流度下的边界层分离由K-H不稳定性主导，随着湍流度的上升，K-H不稳定性的主导性下降。

由于湍流度随着流体从边界入口流向平板的过程中会略有降低，本文设置入口湍流度4%，计算得出平板前缘3个参考位置(如图6所示)R1、R2、R3的平均湍流度分别约为3.35%、3.18%、3.07%。预计在该湍流度水平和70 000的入口雷诺数下层流分离泡不会消失。

3 结果与讨论

3.1 平均流场分析

在计算中，单凭残差线不足以作为收敛性的判断，因此选择流向的2个监测点(x/L=0.5和x/L=1, 高于平板平板上表面2 mm)来辅助判断收敛性。最终，除去计算中尚未收敛的起始阶段与可靠性较差的末尾阶段，选取稳定性较好且时间连续的若干周期用于结果分析。通过雷诺平均得到稳定来流条件下的边界层分离状态如图4所示，并在表1中提供稳定来流与周期性来流条件的部分边界层数据。

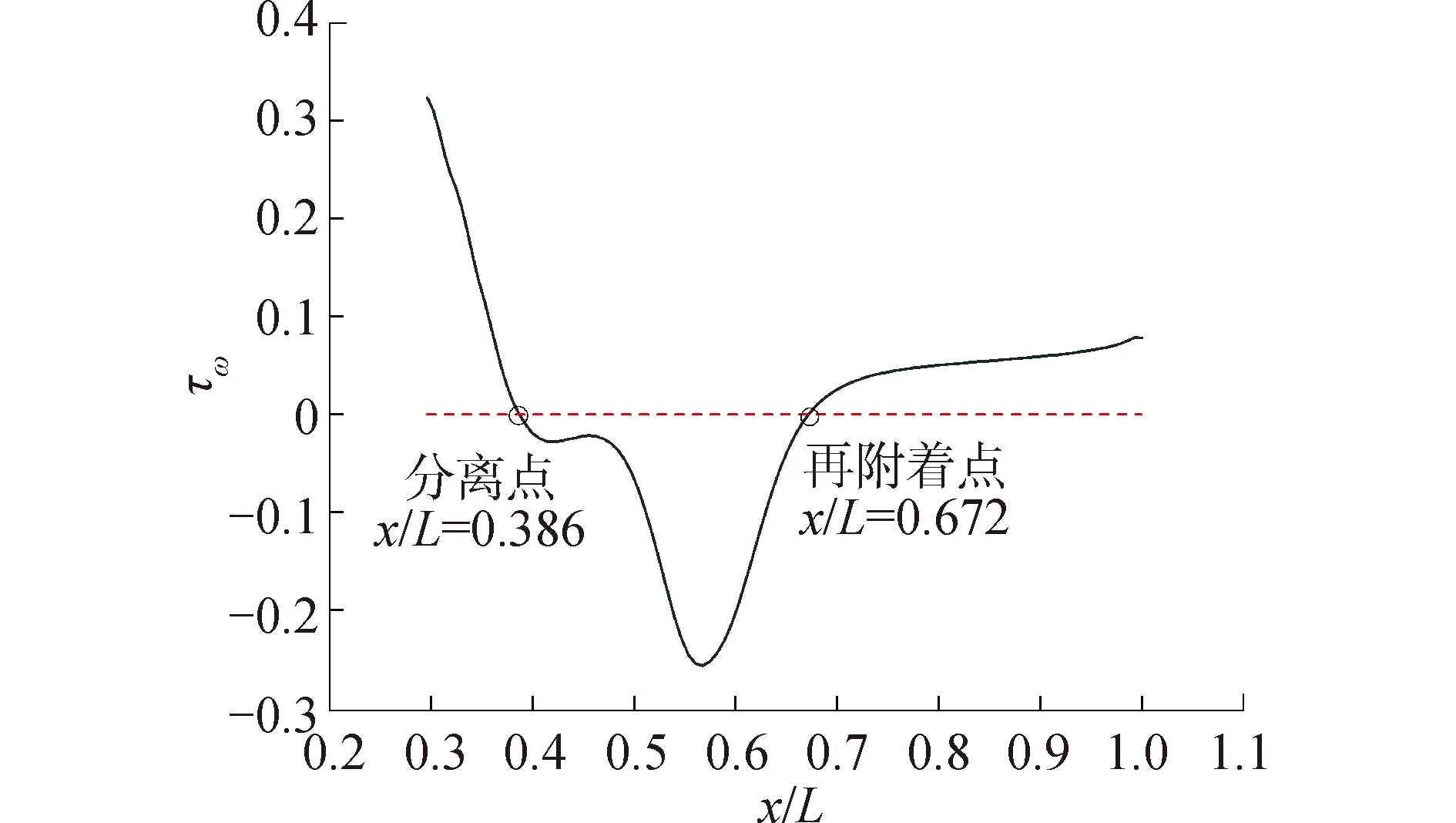
图4 稳定来流状态下壁面流向剪切力分布

表1 2种来流条件下分离区参数对比

稳定来流状态的平均分离点在x/L=0.386左右，f+=0.5的周期性来流条件下平均分离点为x/L=0.382，略提前于稳定来流条件。文献[3]中设置了f+=0.8的周期性来流条件，其实验结果显示平均分离点同样略提前于稳定来流条件。

选择平板表面相距较宽的3个点来计算其速度型线，以查看周期性来流下平板表面发生的流动状态变化，如图5所示。x/L=0.3处的速度型线是典型的牛顿流体层流状态，x/L=0.55处的负向速度型线表征了该区域的流动分离，在平板末端x/L=1处的速度型线则表示了湍流状态。该图表明了周期性来流条件下平板表面的层湍转捩的存在。

图5 周期性来流频率f+=0.5时平板表面3点处速度型线

基于图5估算边界层厚度，设置从点A(x/L=0.3,y/L=0.06)到点B(x/L=1,y/L=0.06)的数据采集线AB线。与x轴平行的AB line将被用于研究速度分布。本文确保该数据采集线穿越近壁的速度震荡区并且有足够的流体填充周围区域。如图6所示。

图6 数据点采集点示意

图7采用雷诺平均方法展示了流向与法向2个速度量在稳定来流与周期性来流条件下沿数据采集线AB线的分布。显然，从全局平均统计来看，低频来流尾迹的周期性作用没有改变平板表面边界层的基本运动趋势，但是导致了局部的流动能量的加强与减弱。对于2种来流条件来说，流向速度最小值区域都位于约x/L=0.55的位置；而对于法向速度最小值，相比于稳定来流条件，周期性来流条件下该区域略向后延迟。

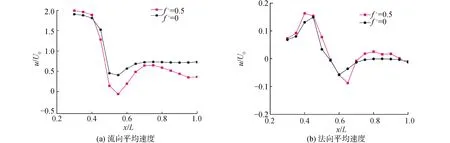
图7 ABline对应的平均速度分布

3.2 分离剪切层运动分析

图8和图9中的涡量云图提供了关于尾迹如何影响边界层演变的清晰过程。扰流棒拖出了一条明显的冯卡门涡街(V-K涡)。图8的各个时刻中，尾迹尚未对边界层产生影响，此时平板表面边界层的内在演变起主要作用。气流在接近x/L=0.4的位置开始分离，以流向条纹的形式，即图中A1区域前的长条结构，到达边界层最高处，并在末端形成大涡。分离剪切层内首先在A1区形成大涡，A1涡沿流向前进至A2区，A2区大涡顺流进入A3区。从t/T=0.05可以发现A1涡的前面壁面处，A1与A2涡之间的壁面处，均有涡尖突起，标记为B1，B2。A涡均为顺时针旋转方向，与此相反的，B系列涡尖为逆时针旋向，但在A1涡的挤压与A2涡的诱导下，B2区涡尖被向上挤压拉伸，成为A2涡的半涡环，并在A2涡进入A3区后成为其全涡环。如t/T=0.075所示，流向条纹末端不断产生新的旋涡，放大，脱落，沿流向推进，伴随B区涡尖环绕脱落的涡沿平板表面上部一定距离的位置流向推进，并伴随能量衰减，该过程周而复始。这一演变过程明显的证明了以大涡为特征的K-H不稳定性的存在。

图8 尾迹作用之前分离剪切层内涡量状态云图

周期性尾迹与平板表面分离剪切层交互作用的过程如图9所示。t/T=0.3是尾迹接触分离区的起点，以t/T=0.425尾迹对分离区最后的影响为结束。通过放大视角观察图10中对分离区交互作用状态，发现在t/T=0.3尾迹接触初始分离区的流向条纹时，尾迹中的V-K涡将流向条纹初始段中的部分能量诱导出原有路径并跟随V-K涡前进。通过观察t/T=0.3与t/T=0.35，有理由认为该V-K涡的诱导过程持续了整个流向条纹阶段。在尾迹涡进入分离核心区后，即t/T=0.35，尾迹压制了下方的涡使分离剪切层变窄，同时既拉伸了后方的涡，也强化了B2涡尖，带动尾迹后方的涡伴随迅速强化的涡尖脱离平板表面沿流向运动。由于尾迹对分离区的压迫，条纹末端初始涡短暂地改变了形态，如图10中t/T=0.375所示，但在t/T=0.4时迅速恢复，然而尾迹的前进速度明显高于分离区涡的内在脱落速度，导致了流向条纹末端新生涡的成型过程被压制，紧邻的成型涡被尾迹迅速带走，两涡之间的间距被拉大，该过程周期性变化，使得分离区的实际长度，包括再附着点，也呈现周期性的变化。即使尾迹已经掠过分离区，其动量输入却未结束，表现在t/T=0.425中流向条纹末端本应形成初始涡的区域被拉长成扁平状。在此之后，尾迹对分离区影响消失。尾迹对分离核心区的持续影响时间约为0.125个周期。

图9 尾迹与分离剪切层的交互作用

图10 分离区交互作用放大示意

尾迹对分离区的压制作用导致了反向作用力，使其本身形态发生改变。t/T=0.4时刻尾迹V-K涡与分离区固有脱落涡存在明显掺混状态。平板表面分离剪切层的存在进一步减少了喉部以后的通道截面积，加快了尾迹的前进速度，因此我们看到在尾迹离开分离区后的t/T=0.45至t/T=0.525阶段，图中区域C至E，尾迹通过一种顺时针的卷吸作用对从分离区内率先带出的涡进行了加速与顺时针旋转，使其高于并赶上临近的后部涡，继而导致双涡掺混旋转前进。后部涡被卷吸至下方，导致紧邻的下一个涡更易受到尾迹卷吸，重复作用，得到了图中所示的尾迹离开分离区后对平板表面脱落涡的成对卷吸掺混现象。该作用加快了分离转捩区后部高能涡的能量耗散，加强了湍流的均匀性。

3.3 转捩分析

利用FFT(快速傅里叶转换)来采集AB line上的二维速度信息，得到关于速度波动能量谱密度图11所示。

平板的前端x/L=0.3处未见明显波峰。实际上x/L=0.3之前为顺压区，本身不太可能出现T-S波。x/L=0.3之后为逆压区，若此时存在T-S波则应在平均分离点x/L=0.382之前出现明显的波峰，但即使到x/L=0.45处，依然没有明显的波峰。文献[5]的研究显示在平板前缘湍流度2.9%的状态下T-S不稳定性阶段被绕过了。由于本文平板前缘的湍流度略高于该数值，有更大概率绕过T-S不稳定性。该文献同时认为流向条纹的出现是T-S波被绕过的征兆之一。从x/L=0.5开始30 Hz段的低频能量显著增强，高频波峰逐渐趋显，说明分离过程趋于严重并伴随内部涡的产生。从流向平均速度曲线来看，x/L=0.55附近应为分离剪切层最大厚度的位置，从PSD曲线看，此时低频波峰最为明显并伴随微弱的高频波峰，表明该位置的边界层分离最为剧烈并占据主导地位，同时伴随一定程度的涡运动。x/L=0.65处出现最为明显的180～200 Hz高频能量波峰，低频波峰消失，该区域附近为涡的脱落扩散最为激烈的区域，表明K-H不稳定性占据转捩过程的主导地位[12-13]。

图11中说明的分离层内能量的能量分布同样在图12中的AB线平均速度波动曲线得到证明。在全局平均尺度下，层流分离泡的上游速度波动能量维持了稳定状态，分离开始后其分离区内部扰动能量迅速上升，至x/L=0.55与x/L=0.65区间高频能量明显显现，如图11中对应阶段波峰的出现。流过高频振荡区后，随着再附着过程和转捩后湍流的扩散，速度振荡能量趋于下降。

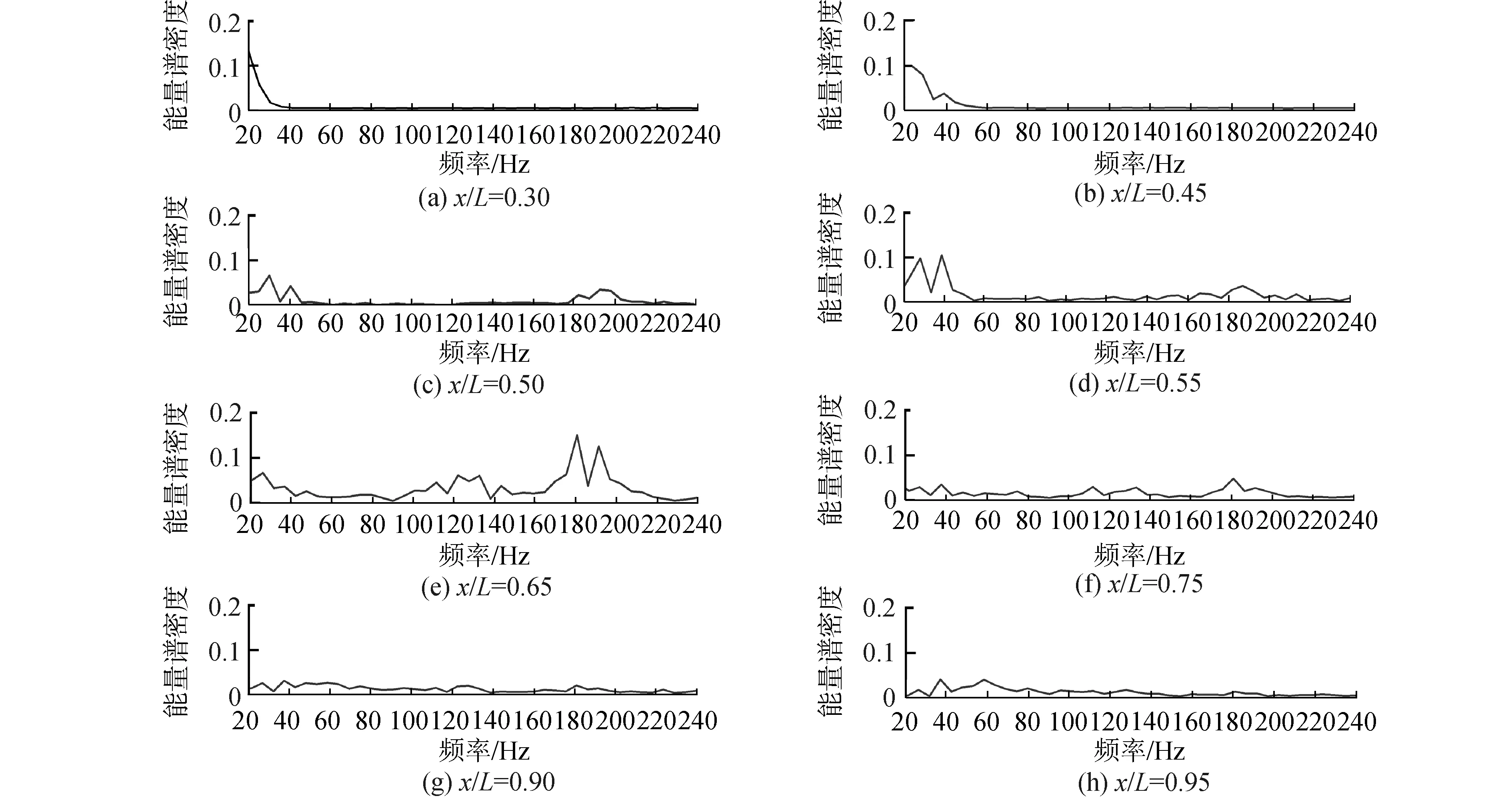
图11 周期性来流f+=0.5条件下边界层的PSD分析

图12 ABline 均方根速度波动分布

在时间与空间的共同尺度下对速度波动能量进行分析，有助于理解分离剪切层在尾迹影响下的演变机理[14-15]。以t/T=0.3时刻尾迹与分离泡前缘接触时为起始时刻，此时的平板表面流线状态如图13所示。在分离转捩区内贴近分离剪切层上层区域沿t/T=0.3时刻尾迹前进方向取9个数据点，计算其速度波动能量变化，如图14所示。

图13 t/T=0.3时刻平板表面速度流线

速度波动的均方根值为图14所示，t/T=0.3时刻的能量沿着时间在分离层内流向推进。随着上游能量的推进与作用，层流分离阶段内速度波动呈现线性上升趋势，并在大约分离区最厚处达到最大。这一过程印证了线性不稳定性的存在。由于尾迹诱导的低频能量被引入分离剪切层后被逐步放大至高频能量，速度振荡能量呈指数上升趋势，如图14所示，这与文献[3]的实验分析结果一致。速度波动能量在经过x/L=0.6～0.65区间后趋向下降，表明这一区间能量振荡的放大达到饱和状态，并诱导转捩，导致下游能量振荡水平的下降。

图14 分离转捩区受t/T=0.3尾迹作用的时间-空间能量变化曲线

4 结论

1)相比于无尾迹的稳定来流状态，周期性尾迹来流条件略微提前了平板表面的气流分离点，再附着点由于尾迹的带动卷吸作用呈现多点周期性后移现象，难以有相对确定位置。

2)分离核心区涡的演变模式为核心涡与间隙涡发展的涡环成对出现，该固有模式受到来流尾迹的促进。

3)尾迹对分离泡的抑制作用表现为尾迹对分离区能量输出使得层流泡内本应形成的初始涡被压缩拉长，但并非贯穿全程，而是呈现周期性特性，在尾迹掠过分离区时产生，约为0.125个扰流棒周期。

4)在平板前缘3%左右的湍流度与f+=0.5的低频尾迹来流条件下，其转捩机理如下：分离转捩区内高能震荡区在x/L=0.65左右，约为180～200 Hz。进入分离剪切层的低频能量在线性不稳定性的作用下指数型放大为高频能量，最终诱导分离区转捩。流向条纹，K-H不稳定性和尾迹振荡能量的输入共同导致了边界层的转捩，未发现明显的T-S不稳定性。

然而，在稳定来流条件下，足够高的湍流度(>5%)可以导致分离泡消失，但是在具有来流尾迹时，多大的来流湍流度可以导致K-H不稳定性被绕过，则是值得继续研究的问题。