基于致动盘模型的风力机来流风速选取方法研究

任会来，王 聪，黎 波，聂秀利

（1.龙源（北京）风电工程设计咨询有限公司，北京 100034；2.河北省石家庄技师学院，河北 石家庄 050000）

0 引言

随着风电大基地项目的不断增加，大规模风电场尾流效应导致的电量折减和运行安全问题成为研究热点。在单机容量及项目规模不大情况下，传统的线性模型结果是被普遍接受的，但随着单机容量及项目规模的迅速增长，线性模型低估大型风电场尾流的可能性大大增加。近几年出现了多种线性模型改进方法，以适应大型风电场尾流计算。美迪采用的大规模风电场（Large Wind Farm，LWF）模型[1]和AWSTruepower采用的深度阵列尾流模型（Deep Array Wake Model，DAWM）[2]均将风力机的数量和排布方式对流场的影响等效为粗糙度来考虑，有效提升了大规模风电场尾流的计算精度。

随着计算能力的提升，尾流的CFD方法逐渐成为研究热点。然而，由于风力机和风电场物理尺寸的巨大差距，使得网格分辨率跨度和网格数量极大，难以兼顾DNS，LES和DES等方法的高精度与计算的时效性。因此，在一定程度上能够二者兼顾的RANS方法受到了人们的关注，其中可进行定常计算的致动盘方法使用较广。Antonini E G A[3]利用4种湍流模型对3个实际风电场进行了计算，发现致动盘方法所得结果与实测数据较为一致。Gargallo P A[4]分别评估了两种大气边界层条件下的风电场的年发电量，发现致动盘方法所得结果误差较小。Nedjari H D[5]考虑了风力机、地表及大气边界层的相互影响关系，并以实际项目做了验证，发现致动盘预测模型准确度较好。其他专家和学者也对致动盘方法做了较多的计算和研究。Sturge D[6]将致动盘方法和直接构建风轮方法混合使用，有效减小了计算量，同时保证了计算精度。杨瑞[7]以实测功率为基准求得致动盘参数，对4台串列风力机进行了模拟，并给出了多台风力机的布置间距建议。许昌[8]改进了动量源项和耗散率源项，并修正了源项系数，使得计算结果更为精准。

在工程中，风力机的功率和尾流的计算均基于特定的功率曲线，而该曲线的使用方法是基于来流风速的，因此来流风速的选取显得尤为重要。风力机来流选取的方法多为直接提取风力机上游点、面上的数值进行计算[6]。该方法的不足之处是不能确定选取距离，容易同时受到上游尾流和致动盘本身的影响。部分学者以实测数据为基础求得致动盘参数，可不考虑来流风速选取问题[7]。在无实测数据情况下，文献[9]采用反函数方法求得来流风速，但因功率曲线不是规则曲线，该方法须要分段求解以保证精度。本文在顺列和错列排布情况下，分别采用直接提取风力机上游点、面上的数值以及通过致动盘处风速反推这3种方法进行计算，并讨论了3种方法的不同特点。计算结果表明，反推方法可不受取点（或面）距离的影响，适用于致动盘模型计算。

1 致动盘基本应用理论

1.1 致动盘方法

致动盘方法来源于一维动量理论，即将风轮简化为一个圆柱形薄盘，并以体积力的形式实现风轮对流场的作用。体积力与来流风速和推力系数有关。

假设入流风速为u1，则风轮单位面积的轴向力为

式中:ρ，CT分别为对应功率曲线的空气密度和推力系数。

动量方程中，致动盘体积力源项表示为

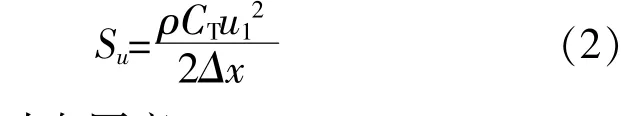
式中:Δx为致动盘厚度。

1.2 致动盘源项修正

多项研究表明，致动盘方法须要进行一定的修正，从而避免尾流恢复过快的问题[8]～[11]。本文采用了其中一种修正方法[12]，即在k-ε湍流模型中同时添加湍流动能和耗散率源项的方法，使流场中湍流动能的生成和耗散得到平衡。

湍流动能源项为

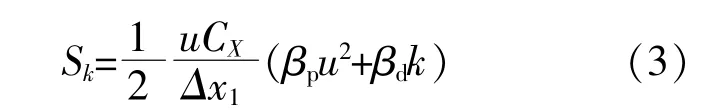
式中:u为致动盘处速度；CX为制动盘的阻力系数，CX=4a/（1-a）；βp为时均动能转化为湍流动能的系数，βp=0.1[0.22+0.122/（1-a）2]（1-a/2a）；βd为湍流动能损失的系数，取值为1.0；Δx1为风轮邻域的厚度；k为湍流动能。

耗散率源项为

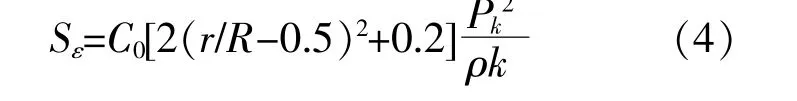
式中:C0为耗散率源项参数，取为1.0；r为网格中心到致动盘轴线的距离；R为风轮半径；Pk为湍流动能生成项。

1.3 来流选取方法

在流场中，来流经过风力机时，由于受到风轮的扰动，速度在风力机附近区域就已经开始下降，因此选取风力机前方一定距离位置的风速作为来流，可以解决由于风力机自身对流场的影响而导致的来流选取问题。选择风力机上游轮毂轴线上的一点作为来流的取值点，或选择以该点为中心，以风轮半径为半径的圆面作为来流的取值面，此方法下文称为取点（或面）方法。

当流场中有多台风力机时，取点（或面）方法会出现一些问题。由于上游风力机不受尾流影响，只须考虑风轮自身对流场的影响，通过增大取点（或面）距离的方式使所取值接近实际来流。但对于下游风力机时，该方法不仅要考虑风力机自身对来流的影响而增大取点（或面）距离，同时还应考虑上游尾流的影响而控制取点（或面）距离，使点（或面）尽量不在上游风力机的尾流区，因此取点（或面）距离难以选择。同时，由于风轮自身对流场的影响，使得风轮前方的速度永远是无限接近但小于实际来流的，简单的采用取点（或面）方法无法得到真实的来流。因此，出现了通过致动盘处风速反过来推算来流的方法，如采用反函数方法和迭代方法[9]，[12]，即以致动盘位置的平均风速为基准，通过风速-推力系数一一对应关系反推来流的方法。

2 数值计算

2.1 计算设置

计算域为矩形（图1），布置了两台风力机进行计算。X方向（平行于来流）长度为30D（D为风轮直径），Y方向（垂直来流）为7D，Z方向（垂直方向）为10D。X方向网格分辨率在致动盘处最高，为1 m，延展比为1.1；Y方向网格分辨率为均匀的10 m，最小；Z方向网格分辨率在地表最高，为1 m，延展比为1.1。此时致动盘网格数量约为170个，总网格量为114万。

图1 计算域示意图Fig.1 Computational domain

来流风速采用取点（或面）方法时，取值位置设为上游距致动盘分别为0.5D，1D，1.5D和2D 4种距离的点（或面）上的速度值。计算采用两种排布方式:①两台风力机顺列排布时，顺风向间距为7D，垂直风向间距为0；②两台风力机错列排布时，顺风向间距为5D，垂直风向间距分别为0，0.25D，0.5D，0.75D和1.0D 5种。

风力机选用某厂家3.0MW-156低风速机型，轮毂高度为120 m，D为156 m，功率曲线和推力系数曲线如图2所示。

图2 功率曲线和推力系数曲线Fig.2 Power and thrust coefficient curves

2.2 边界条件

风力机运行于大气边界层内部，在边界层中，风速u、湍动能k及其耗散率ε均沿高度变化，直到大气边界层顶部。

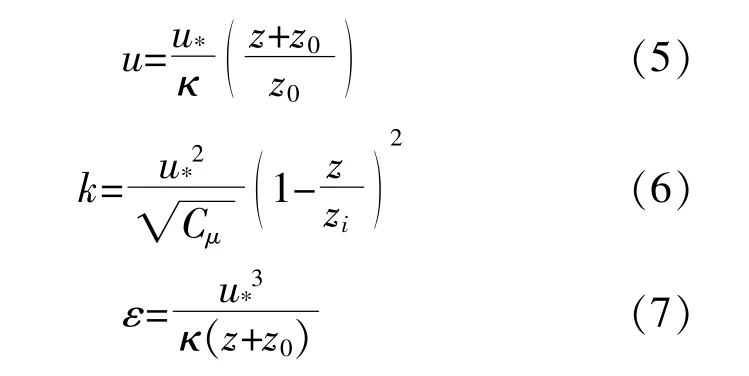
式中:u*为摩擦速度；κ为冯卡门常数，取0.4；z为从地表向上的高度；Cμ为湍流模型系数，取0.03；z0为地表粗糙度；zi为大气边界层高度，zi=u*/6f，f为科氏力参数，f=2Ωsin（|λ|），Ω为地球自转角速度，λ为当地纬度。

实验数据一般只提供入口轮毂高度处的风速和湍流强度，因此须要补充湍流强度和湍流动能的关系。

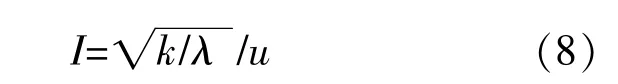
式中:λ为模型常数，对于各项同性的湍流取值为1.5。

为简化计算，风力机顺列排布时，实际来流风速分别取为6，8 m/s和10 m/s；风力机错列排布时，来流风速取为8 m/s，湍流强度均为0.11。采用较为广泛的k-ε湍流模型进行计算。

2.3 计算结果

2.3.1 顺列排布

图3所示为不同来流风速条件下，取点（面）方法的结果对比曲线。

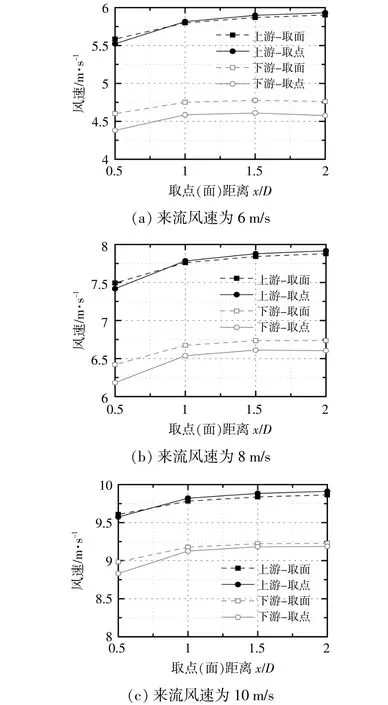
图3 不同来流风速条件下，取点（面）方法的结果对比Fig.3 Comparison of the results with the point（surface）-take method under different inflow wind speed

由图3可知:在顺列排布情况下，通过取点和取面两种方法所得上游风力机的来流速度相近（差值小于0.05 m/s），来流速度随取点（或面）距离的增加而增大，但趋势渐缓，并逐渐接近实际来流，其最大误差为4%～8%，出现在取点（或面）距离为0.5D位置处；下游风力机的来流变化趋势与上游风力机相似，但由于受到上游风力机尾流的影响，数值整体偏小。

随着实际来流速度的增加，上、下游风力机的来流速度之差也出现一定的变化（0.6～1.0 m/s），这是由于受到风力机运行策略的影响。在功率爬升阶段（切入风速至接近额定风速段），如来流风速为6 m/s和8 m/s两种情况时，风力机以捕获最大风能为目标，此时桨距角不变，但风轮转速变化，使风能利用系数稳定在最佳值，因此风速差较大且稳定。当实际来流接近额定风速时，如来流风速为10 m/s时，桨距角和风轮转速都变化，使风能利用系数降低，功率稳定在额定值，因此可认为上、下游风力机的来流速度之差随实际来流速度增加而减小。

由于受到风力机运行策略的影响，在功率爬升阶段，推力系数维持在一个较高的数值，对流场的影响也较大，因此通过两种方法所得下游风力机的来流速度出现明显差异，约为0.2 m/s。当实际来流接近额定风速时，两种方法所得下游风力机的来流速度接近，差值低于0.05 m/s。

与取点方法相比，取面方法所得上、下游风力机的来流速度化范围更小，更稳定。

图4所示为不同来流风速条件下反推方法的结果对比曲线。与取点（或面）方法结果不同，反推方法所得上游风力机的来流与实际来流较为一致，当来流风速为6 m/s时，差值低于0.03 m/s，误差约为0.6%。同样由于受到风力机运行策略的影响，上、下游风力机的来流速度之差随实际来流速度增加而减小（从0.8 m/s降至0.4 m/s左右）。

图4 不同来流风速条件下反推方法的结果对比Fig.4 Comparison of the results with the inverse method under different inflow wind speed

2.3.2 错列排布

图5所示为不同错列间距条件下，取点（面）方法的结果对比。

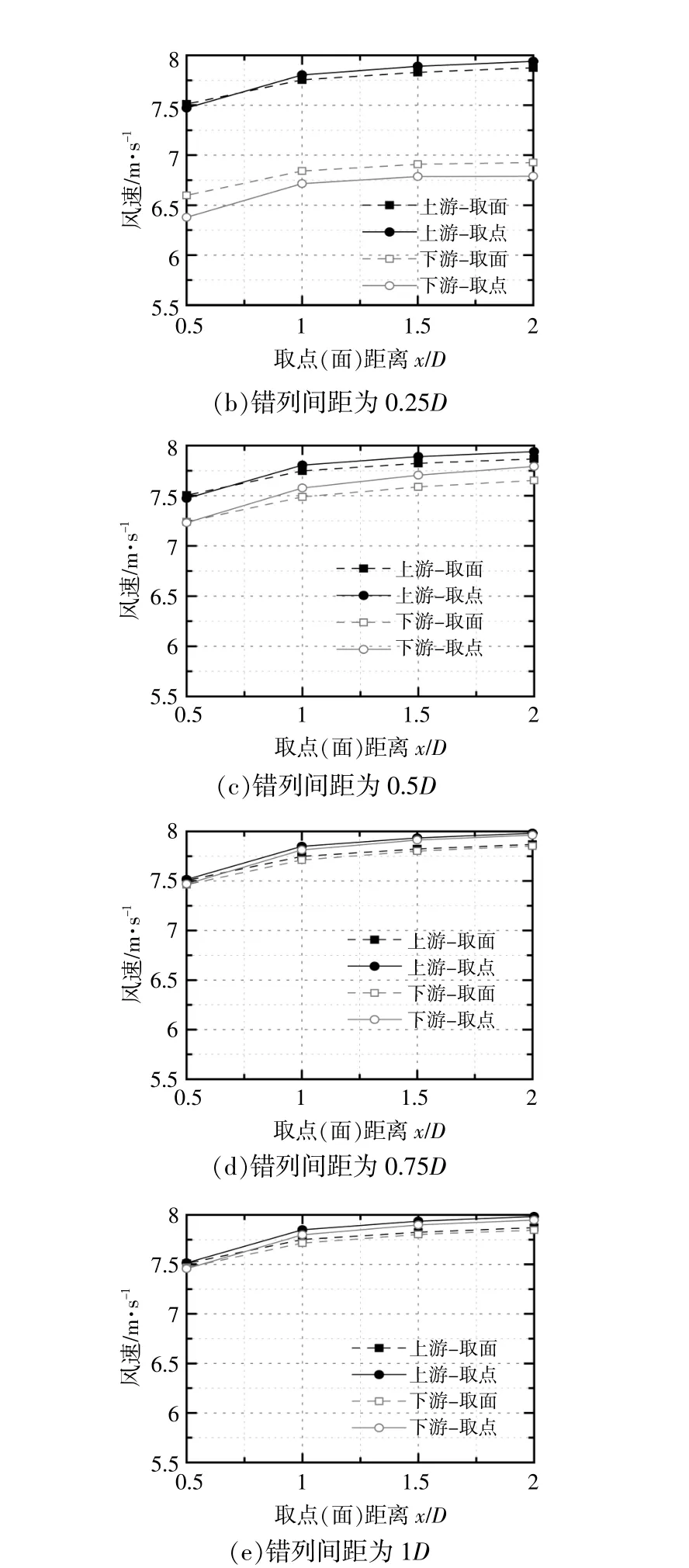
图5 不同错列间距条件下，取点（面）方法的结果对比Fig.5 Comparison of the results with the point（surface）-take method under different staggered spacing

由图5可知:与顺列排布相似，通过取点、面两种方法所得上游风力机的来流速度，随取点（或面）距离的增加而增大，但趋势渐缓，并逐渐接近实际来流，其最大误差为6%～7%，出现在取点（或面）距离为0.5D位置处；下游风力机的来流速度变化趋势与上游风力机相似，随取点（或面）距离的增加而增大并逐渐接近一个稳定值。

随错列间距的不断增加，通过取点、面两种方法所得上游风力机的来流速度之差也逐渐增大（从0.03 m/s增长至0.11 m/s），同时上、下游风力机的来流速度之差由1.5～1.7 m/s（0间距情况）迅速减小至接近0（0.75D和1D间距情况）。这是由于随错列间距增加，上游风力机的尾流对下游风力机位置处的流场影响快速减小，速度场逐渐均匀，使得差值接近为0。

随错列间距增加，取点、面两种方法所得下游风力机的来流速度之差逐渐减小，从约0.25 m/s（0间距情况）逐渐减小至约0.1 m/s（0.75D和1D间距情况）。这同样是由于下游风力机位置处的速度场逐渐均匀，使得两种方法的差值逐渐减小。

与顺列排布相似，取面方法所得上、下游风力机的来流速度化范围更小，更稳定。

图6所示为不同错列间距条件下，反推方法的结果对比曲线。

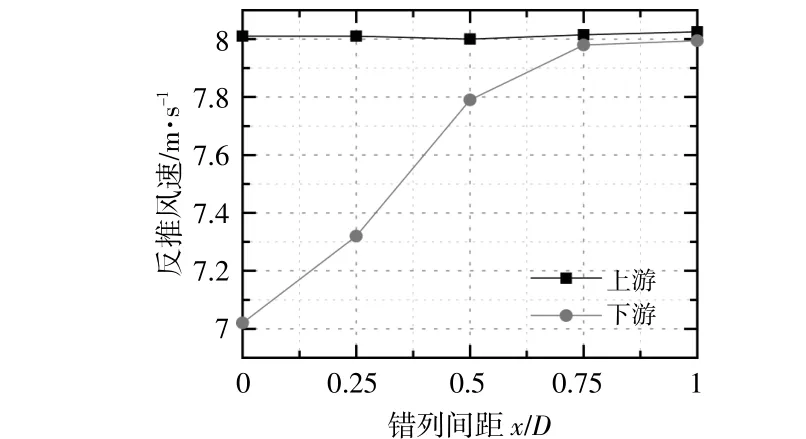
图6 不同错列间距条件下，反推方法的结果对比Fig.6 Comparison of the results with the inverse method under staggered spacing

由图6可知:与取点（或面）方法结果不同，反推方法所得上游风力机的来流与实际来流较为一致，差值低于0.025 m/s，误差约为0.3%，出现在错列间距为1D情况下；同样随错列间距增加，下游风力机的来流速度迅速减小至接近0（0.75D和1D间距情况）。

顺列和错列排布是风电场工程中常见的布机方式，通过对这两种排布方式进行计算分析，反推方法可以得到准确的上游来流数据，并可忽略取点（面）距离的问题。

3 结论

由于较少有文献以致动盘模型为对象研究风力机来流风速选取方法之间的差别，因此本文选用了取点、取面以及反推3种来流选取方法进行了计算，分析了3种方法所得结果的特点，并得到如下结论。

①通过取点（或面）方法计算时:上游风力机的来流速度小于实际值且不稳定，相对误差为4%～8%，并随取点（或面）距离增加而增大；在功率爬升阶段，上、下游风力机的来流速度之差较大且稳定，当接近额定风速后，差值随风速增加而减小。

②与取点方法相比，取面方法所得风力机的来流速度范围更小。而反推方法所得风力机的来流与实际来流较为一致，相对误差低于0.6%，远低于取点（面）方法，且不受取点（或面）距离影响，更适用于致动盘模型计算。