超空泡航行体三相流动演化特性
2022-02-16王威侯瀚程何广华杨豪
王威, 侯瀚程, 何广华,2, 杨豪
(1.哈尔滨工业大学(威海) 海洋工程学院,山东 威海 264209; 2.山东船舶技术研究院,山东 威海 264209)
水下航行体借助通气超空泡的包裹,可大幅度地减小摩擦阻力[1],提升航行体的运动速度。前苏联依靠这种技术于1960年研制出航速高达200 kn的“暴风”超空泡鱼雷,并于1977年装备部队。超空泡水下武器的发射方式多样、突防性强、破坏力大。同时超空泡在水下航行体减阻和降噪领域的潜在应用受到了国内外学者的广泛关注[2]。
自然超空泡是航行体在高速运动中,其周围流体因压力降低到其饱和蒸汽压以下时产生的空化现象,当空泡尺度扩张到足以包裹航行体自身时,形成超空泡。自然超空泡理论上可以采用降低环境压力或者提高航速来实现,降压法往往存在于实验条件下,而提速法比较实际,如美国的高速射弹武器就是利用这种方式实现了自然空泡对航行体的整体包裹,减小弹体的水下摩擦阻力[3]。小尺度射弹易应用自然超空泡减阻,而鱼雷的尺度较大,即使航速达到100 m/s时所生成的自然空泡仍有可能只是覆盖鱼雷头部局部区域,无法形成对整个鱼雷体的包裹[4]。为解决该难题,Reichard[5]提出的主动通气形成通气超空泡技术;就是在空化器后部通入不可冷凝气体(如:空气),依靠提高空泡内部压力的方法在流速较低的条件下实现对航行体的整体包裹。实验表明,在同等空化数下,通气超空泡与自然超空泡具有相似的空泡形态[6]。
通气空泡在实验条件下容易形成,尺度易于控制,在研究空泡形态方面效率很高。Karn等[7]实验研究发现:通气空泡有4种稳定状态的闭合形式和5种不稳定状态的闭合形式。Lee等[8-9]通过实验研究了来流扰动作用下对通气超空泡的形态特性。段磊[10]研究了通气空泡的流场结构,对空泡尾流区域的漩涡结构、脱落空泡团、尾迹等做了深入分析。
数值模拟对研究空泡流动有着独特的优势,如:可以清晰地给出空泡内部的流动结构。Wang等[11-12]通过数值模拟方法研究了空泡的尾流结构,分析了空泡尾涡方向的变化特性。李聪慧等[13]数值研究了航行体纵平面回转运动的空泡形态及泡内压力分布规律。李懿霖等[14]研究了空化器直径对空泡性能的影响。段磊等[15]研究了航行体通气超空化发展初始阶段的流场结构。Guo[16]利用二维轴对称模型初步研究了航行体从自然空泡到通气空泡的流动特性。
航行体通气空泡形成后,其周围的自然空化现象往往消失,已发表的文献对空泡问题的研究常常将问题简化为水蒸汽和水或者空气和水的两相流动问题。实际上超空泡鱼雷(如:暴风)在发射后的加速阶段,加速发动机点火,鱼雷的航速迅速增加到巡航速度,在该阶段中开始主动通气,鱼雷由局部空化迅速发展为超空泡状态[17]。在这个加速阶段,如果航行体的尺度较小,存在自然超空泡向通气超空泡过渡的情况;如果尺度较大,存在局部自然超空泡向通气超空泡过渡的情况。这个过程非常短暂且复杂,流场中涉及到水蒸汽、水、空气的三相流动状态,航行体周围的流场结构和流体动力情况有待于进一步研究与明确。本文将针对这一短暂的非定常复杂过程,开展三维通气空化三相流动的研究,并分析空泡形态的演化过程和流体动力的变化规律。
1 数值模型
1.1 控制方程
本文的流动介质包括水、空气、水蒸汽三相,根据空泡多相流动的研究经验[11-13],本文的数值模拟采用流体体积函数(VOF)多相流模型。
1) 连续性方程:
(1)
式中:ρm=αwρw+αaρa+αvρv为混合介质的密度;αw为水的体积分数;αa和αv分别为空气和水蒸汽的体积分数;αw+αa+αv=1;ρw为水的密度;ρa和ρv分别为空气和水蒸汽的密度;ui为混合介质在笛卡尔坐标轴i方向上的速度分量;xi为i轴方向的坐标,i=1,2,3;t为时间。
2) 动量方程:
(2)
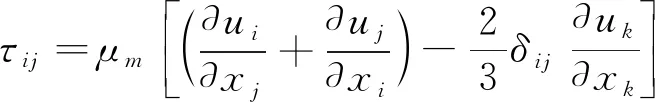
3) 体积分数方程:
(3)
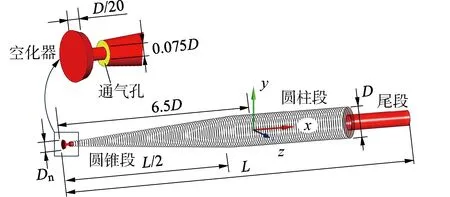
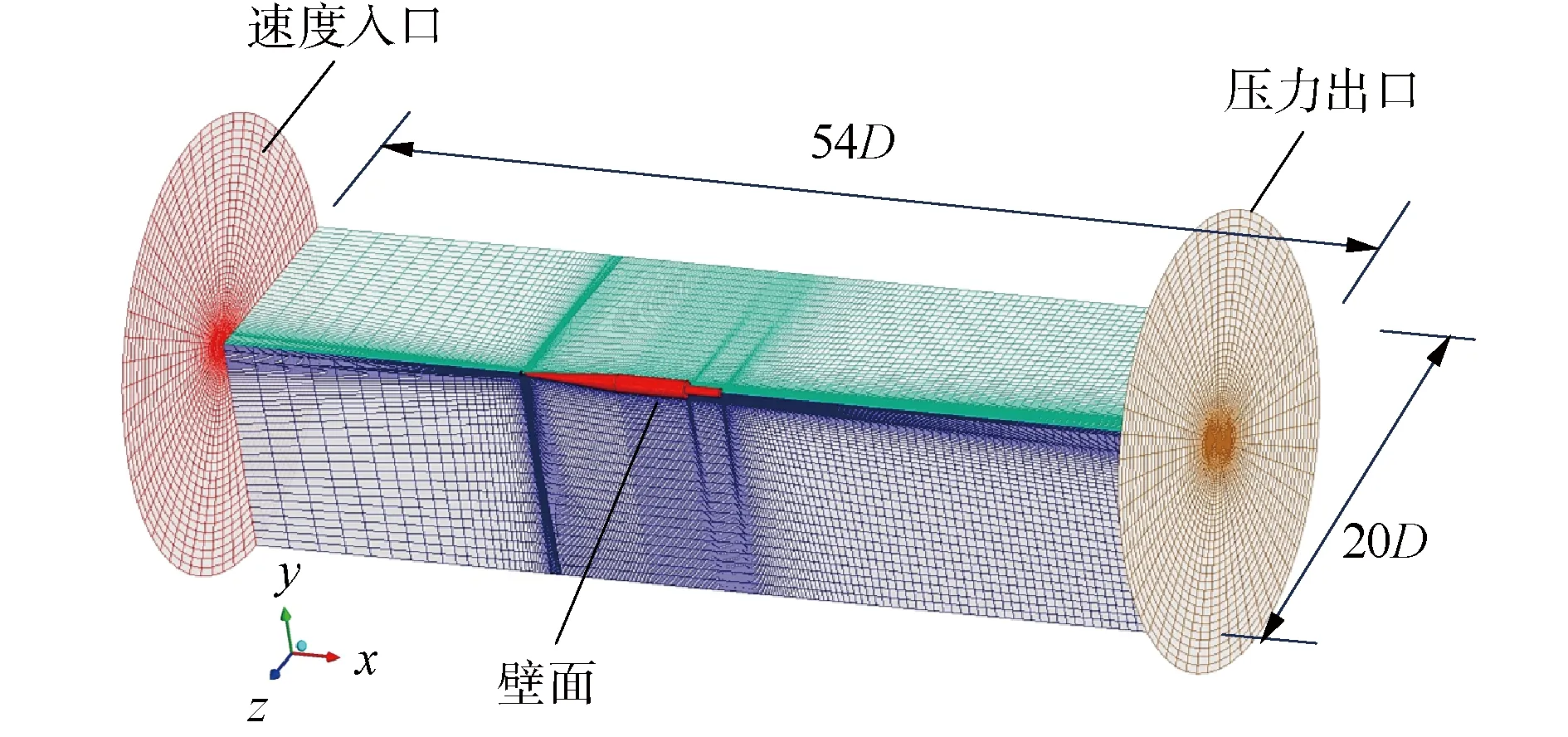
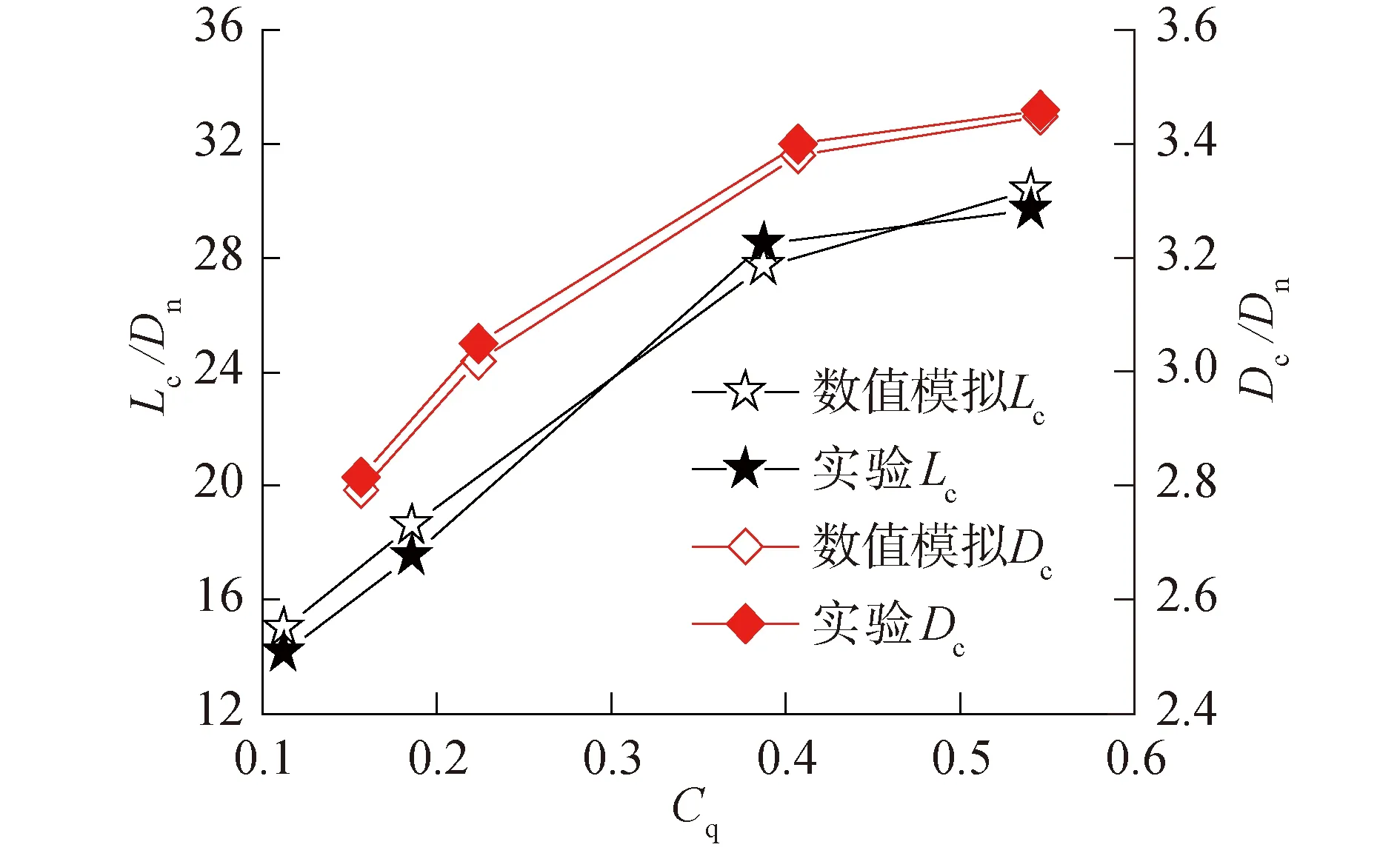
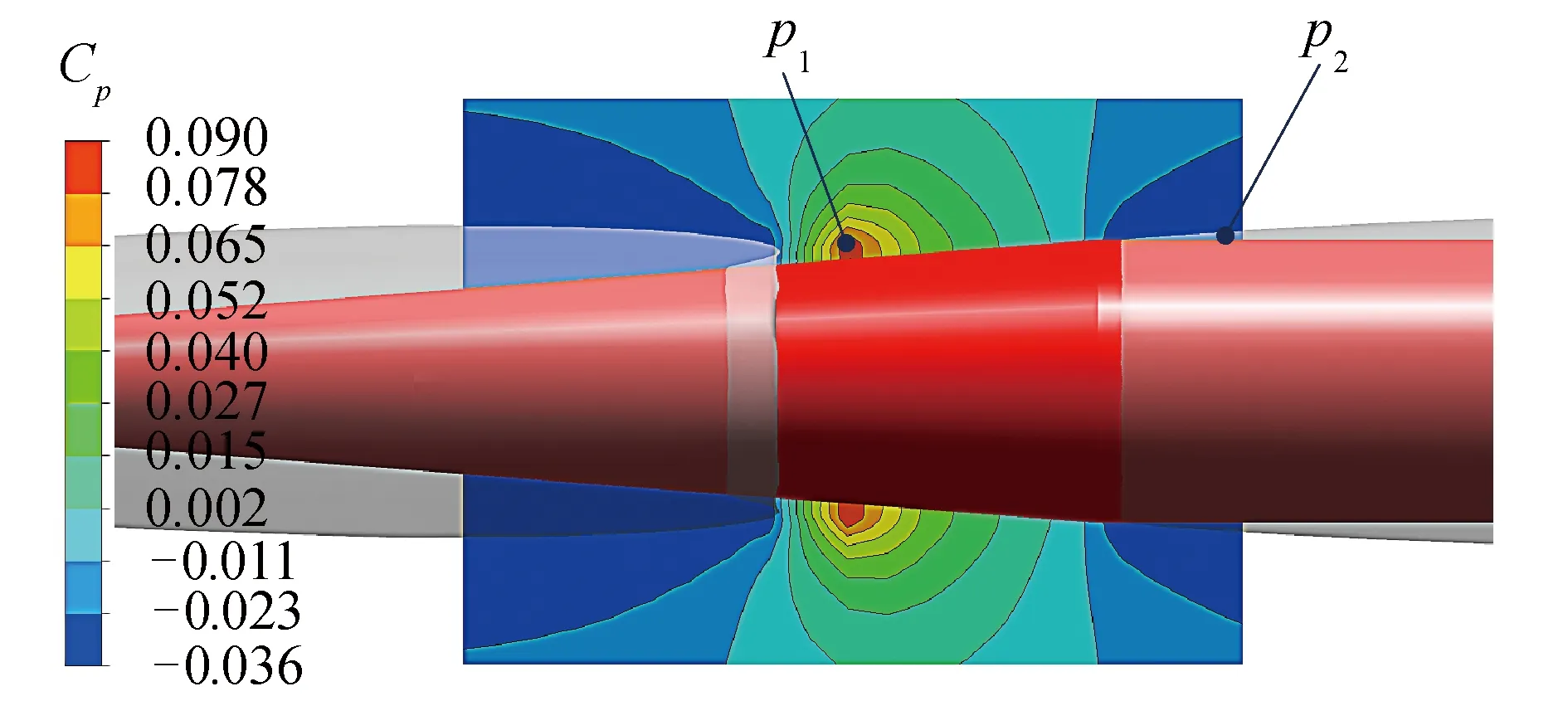
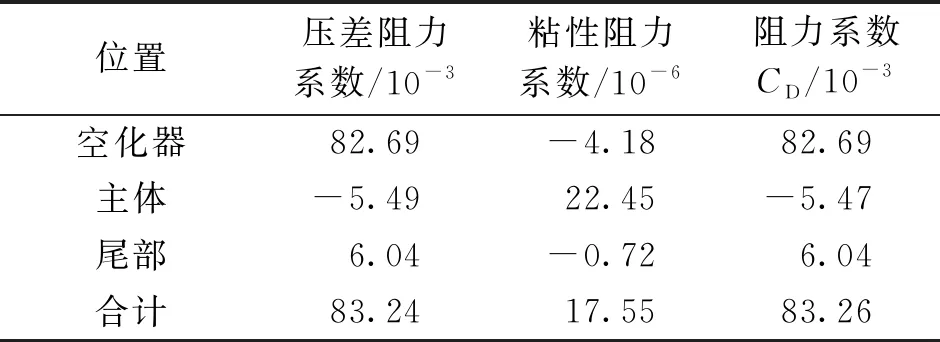
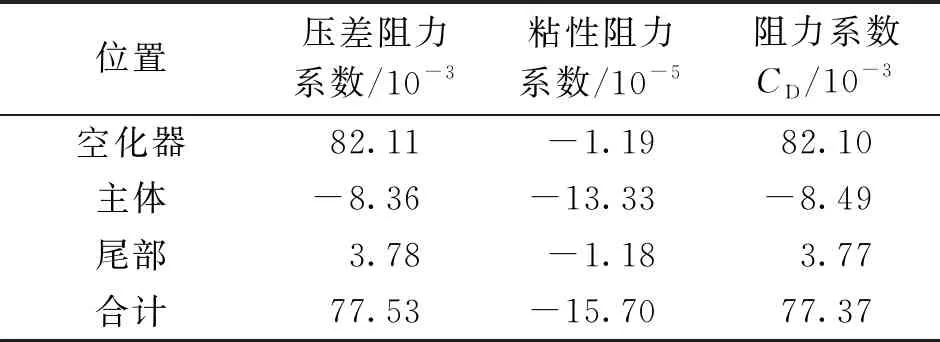
式中:网格单元充满水,则αw=1;网格单元充满其他气体,则a=0;网格单元中包含气体和水的分界面,则0 4) 湍流方程。 数值模拟采用RNGk-ε湍流模型,可以较好地处理文中高应变率和弯曲程度较大的流动,湍动能k和湍动能耗散率ε的输运方程为: Gk+Gb-ρmε (4) (5) 5) 空化输运方程。 选用空化领域应用较广的Zwart模型,通过蒸发源相和凝结源相之间的输运关系来表征两相之间的转换,空化流场内蒸汽相体积分数av的输运方程为: (6) Zwart空化模型是以Rayleigh-Plesst方程为基础推导的,将该模型应用在空泡流动问题时,添加了表面张力和粘性力之后为: (7) 式中:RB为汽(气)泡半径;ζ为汽相与液相之间的表面张力系数;pv(T∞)为水的饱和蒸汽压。 航行体模型如图1所示,从前到后依次为圆盘空化器、圆锥段、圆柱段、尾段组成。航行体直径D=40 mm,全长L=12D,空化器直径Dn=0.3D,航行体质心距空化器前端6.5D,通气孔位于圆锥段头部,朝向空化器背向。 图1 航行体模型 圆柱形流动计算域长度为54D,直径为20D,整个流域采用结构化网格,最小网格尺度由航行体向流域边界逐渐稀疏,如图2所示。流域前端及圆柱面均为速度入口条件,流域末端为压力出口边界条件,按照水深4 m设置,重力加速度沿y轴向下,航行体表面为壁面条件,通气孔为质量入口条件。计算前反复调整流域的网格数量及时间步长,使计算结果收敛,网格数量选为71万,最大时间步长Δt=1×10-4s。 图2 计算域及边界条件 文中的通气率系数Cq=Q/(u∞D2),Q为气体体积流量,u∞为来流速度。根据文献[18]的水洞实验结果,在相同Cq和u∞条件下,数值模拟经典的空化器模型结果和实验结果对比如图3和图4所示。 图3通过实验和数值模拟分别给出了空泡形态发展的过程,上方是实验结果,下方是数值模拟结果(αw=0.5作为空泡界面),空泡形态相似度较好。图4给出了空泡尺度的对比结果,空泡长度Lc和直径Dc的曲线变化规律一致,并且数值模拟和实验结果相差6%以内。图3和图4表明数值模拟结果与实验结果吻合度较高,文中的数学模型可以很好地预测超空泡流动现象。 图3 实验结果和数值模拟结果对比 图4 实验和数值模拟的空泡尺度对比 图5 自然超空泡形态演化过程 从图5可见,航行体在初生空化时刻仅有空化器、圆柱段、尾段的后边缘产生少量自然空泡(σ=0.038);随着时间推移,这些空泡逐渐增大,肩部也出现了自然空泡,并且航行体尾部台阶处空泡在扩大的过程中逐渐融合成一个尾空泡(σ=0.034);随着肩部空泡的扩大,肩空泡又开始和尾部空泡逐渐融合新的肩部空泡(σ=0.033);最后,随着头部空泡的发展,又和肩空泡融合为一体(σ=0.031),直至整个自然超空泡完全形成,空泡内部的水蒸汽包裹了整个航行体(σ=0.024)。 前方和后方空泡融合过程中,会存在后方空泡溃灭的情况,以σ=0.033的工况为例,融合位置附近的流场压力分布如图6所示。头部空泡的闭合位置会形成局部的高压区,其压力p1高于水的饱和蒸汽压(没有发生自然空化),而肩部自然空化形成的空泡,其内部压力p2低于水的饱和蒸气压。随着空泡尺度的发展,前方高压区会逐渐向肩部空泡内的低压区靠近。对于本文航行体的肩部位置,当流速较大时(u∞>90 m/s),空化数σ较小,|p1|≪|p2|,两泡接近后,低压区压力始终小于水的饱和蒸汽压,头部空泡和肩部空泡形成融合;而流速较小时(u∞<80 m/s),空化数σ较小,|p1|与|p2|相当,两泡接近后,肩部空泡受到影响,致使压力p2高于水的饱和蒸汽压,肩部自然空泡发生溃灭,头部空泡继续增大。而对于航行体尾段的位置,由于受到航行体形状的影响(台阶),尾空泡内的压力更小,头部空泡和尾部空泡融合时的速度还可以更小一些(u∞>60 m/s)。 图6 空泡融合位置流场压力云图 航行体空泡形态的变化必将带来流体动力的改变,阻力和升力系数为: (8) 式中:Fx和Fy分别为航行体的阻力和升力;A为航行体的最大横截面面积。 图7给出了航行体阻力和升力系数的时历曲线,图7(a)中的阻力系数略有上升是因为流动尚处于提升阶段,随着流速稳定,自然空泡逐渐包裹航行体,阻力逐渐下降,CD从最高值的0.31降低到0.083(自然超空泡),可见超空泡起到了大幅度减小阻力的作用。图7(b)中航行体的升力系数CL在自然空泡形成阶段虽受到汽水两相流场的综合影响出现了剧烈波动,但数值较小,自然超空泡形成后,升力几乎为零。 图7 自然空化航行体水动力系数时历曲线 自然超空泡的稳定性受到速度的制约,速度的变化极易引起空化数的改变,进而带来空泡尺度的变化。实用中可以在自然空泡内部通入不可冷凝气体(如:空气)逐渐替代。主动通气的方法可以根据空泡对航行体的实际包裹程度调节气体流量,使空泡更加稳定。文中通气率系数Cq=Q/(u∞D2),Q为空气体积流量,Cq从0逐渐增大至0.125并保持稳定,在空气通入自然超空泡后,空气的分布情况如图8所示,给出了空气逐渐替换水蒸气的演化过程,tA=1 ms时空泡的主要成分为水蒸气,tA=141 ms时空泡的主要成分为空气,他们的体积分数都取值为0.5,tA为通气时间,从通气开始计时。 图8 通气空化三相流动演化 空化器后部的通气孔附近因空气的注入压力偏高,水蒸汽所占的比例较小,主要以空气为主,但空化器后部绝大部分区域的压力较低,水蒸汽分布比较稳定(tA=1 ms)。Cq较小时,航行体头部的低压区范围较大,自然空化产生的水蒸汽夹杂着少量的空气在水流的带动下迅速涌向下游,并从空泡尾部排出。通气率Cq增大后,航行体头部空化程度减弱,空气注入自然空泡后,以云块状的形式散布于自然空泡表面,并沿表面向尾部流动(tA=17 ms)。自然空泡内部的压力普遍低于外部,并且空泡内距离空化器越远位置的压力相对越大,自然空化程度越弱,所以注入的空气会从空泡的尾部开始堆积(tA=31 ms)。随着空气比例的继续扩大,泡内压力升高,自然空化逐渐减弱,通气空泡由后向前逐渐替代了自然超空泡(tA:57~141 ms)。 通气开始时,少量空气掺入水蒸汽中会减弱自然空化程度,使空化数稍微升高;随着空气的继续注入,空泡内部的压力逐渐升高,直到空气全部替代水蒸汽时,空化数σ仅降低了0.13%,说明自然超空泡过渡到通气超空泡的整个过程中,空化数变化小,空泡尺度变化不大,不影响对航行体的包裹作用。 通气空化三相流动过程中航行体的升阻力变化如图9所示。航行体的阻力随着通气时长的增加逐渐减小,CD从0.083降至0.077 6,减少约0.54%;航行体的升力在57 ms后出现了小幅度波动,CL的变化幅值只有10-4级别,这是因为空气从自然空泡尾部逐渐发展到圆柱段位置,泡内气压逐步升高,空气流动引起的。从升阻力的时历曲线可见,自然超空泡向通气超空泡转化的过程中,主动通气的影响较小。 图9 通气空化航行体水动力系数时历曲线 为分析自然超空泡与通气超空泡的减阻特性,分别提取空化器、航行体主体(圆锥段和圆柱段)、尾段的阻力系数,并将计算测得的压差阻力和粘性阻力分别分析,如表1和表2所示。 比较表1和表2可知,超空泡航行体阻力的主要来源是空化器的压差阻力部分,在自然超空泡和通气超空泡的不同条件下,空化器的压差阻力仅相差0.7%,说明通气空化三相流动中,主动通气对空化器总阻力的影响较小。 表1 自然超空泡条件下航行体的阻力情况 表2 通气超空泡条件下航行体的阻力情况 在自然或者通气超空泡的包裹下,航行体的粘性阻力的数量级都很小,在粘性阻力对应列中,航行体的主体占比比较大,在自然超空泡被通气超空泡替换过程中,粘性阻力与压差阻力相比,其占总阻力的比值始终为小量,说明航行体依靠超空泡的包裹,大幅度降低了粘性阻力。 中大尺度的航行体(直径大于100 mm[17])往往在空化器、航行体的尾段存在局部自然空泡,为节约航行体的动力消耗,并及时利用空泡达到减少摩擦阻力的目的,也可在局自然空泡的内部主动通入不可冷凝气体(如:空气或发动机尾气),使局部自然空泡成为局部通气空泡,并进一步发展形成通气超空泡,快速达到为航行体减阻提速的目的。 1)航行体自然超空泡形成过程中,存在头部空泡、肩部空泡、尾部空泡的融合现象,空泡的闭合位置存在高压区,为避免后方空泡因高压区的影响而发生在溃灭,应适当提高航行体运动速度。 2)通过航行体头部向自然超空泡内注入空气,空气会先在自然超空泡的尾部集聚,然后向航行体的头部逐渐替换掉水蒸汽,直至整个自然超空泡被通气超空泡完全取代。 3)航行体由自然超空泡向通气超空泡演化过程中,总阻力会进一步小幅度减小,通气超空泡进一步提升了航行体的减阻效果。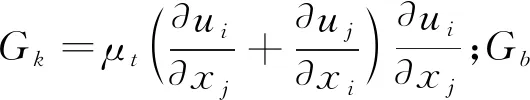
1.2 流域边界条件
2 模型验证

3 数值结果与分析
3.1 自然超空泡两相流特性
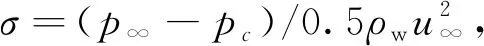

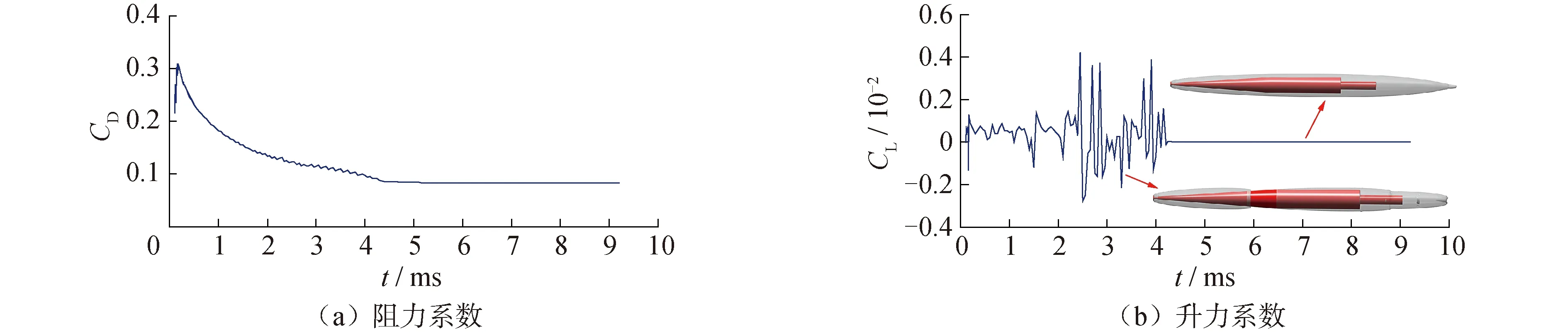
3.2 自然超空泡-通气超空泡三相流特性


3.3 自然超空泡与通气超空泡的减阻特性
4 结论
