一种基于独立膨胀原理的三维超空泡形态计算方法

宋书龙, 万亚民, 李建辰, 周景军, 吕 瑞



一种基于独立膨胀原理的三维超空泡形态计算方法

宋书龙1,2, 万亚民1, 李建辰1, 周景军1, 吕 瑞1

(1. 中国船舶重工集团公司 第705研究所, 陕西 西安, 710077; 2. 水下信息与控制重点实验室, 陕西 西安, 710077)

针对超空泡鱼雷机动过程中流体动力计算需实时准确预报出三维空泡形态的问题, 文中基于空泡截面独立膨胀原理, 提出了一种三维非定常超空泡形态计算方法。通过与Logvinovich模型和计算流体力学(CFD)数值仿真方法的对比, 验证了该方法的合理性。采用该方法对鱼雷的变速运动, 变深运动, 横、纵平面沿正弦轨迹运动及三维空间内螺旋运动的三维空泡形态进行了仿真分析, 仿真结果表明, 文中方法可以预报超空泡鱼雷沿任意轨迹运动的三维非定常超空泡形态。相较于Logvinovich模型和CFD数值仿真方法, 该方法可以求解信息更全面的三维空泡形态, 并可节省大量的计算资源。文中所做研究可为工程实践快速提供时变的三维超空泡形态, 并可为超空泡鱼雷动力学模型的建立提供参考。

超空泡鱼雷; 独立膨胀原理; 三维超空泡形态; 流体动力

0 引言

超空泡鱼雷航行过程中, 由于各种影响因素的存在, 空泡形态于纵平面和横平面都可能发生变形, 在二维平面内无法对超空泡形态进行全面的描述, 因此三维超空泡形态的研究具有重要意义。

目前, 随着计算机技术的快速发展, 计算流体力学(computational fluid dynamics, CFD)的数值仿真方法在研究空泡方面展现出巨大的生命力, 它通过计算机数值计算和图像显示的方法, 可在时间和空间上给出空泡流的定量描述, 能够得到较为准确的三维空泡形态[1-2]。然而, CFD的数值仿真方法对计算机性能要求较高, 计算量较大, 主要应用于超空泡流的机理性研究。而基于势流理论的独立膨胀原理作为超空泡领域的经典理论, 能够反映细长超空泡流动的本质和主要特征, 其合理性已被大量试验证实, 且其便于数值计算的优势可以实现超空泡鱼雷空泡形态变化和流体动力的实时解算, 因此独立膨胀原理在计算空泡形态方面具有巨大潜力。目前基于独立膨胀原理空泡形态的研究主要是二维平面内的[3-5], 关于三维超空泡形态的研究鲜有出现。

文中基于独立膨胀原理推导得到了可用于变速、变深的空泡径向扩展方程; 给出了各种因素对空泡形态的影响; 由空泡径向扩展方程及各因素造成的空泡轴线偏移规律, 给出了三维超空泡形态的计算步骤; 通过与Logvinovich组合空泡模型和CFD数值仿真方法的对比, 验证了方法的合理性; 采用该方法仿真分析了超空泡鱼雷变深、变速及沿各种复杂轨迹运动的三维超空泡形态, 得到了变速、变深超空泡形态的变化规律。因超空泡鱼雷流体动力与空泡、雷体之间的位置息息相关, 因此文中计算的三维超空泡形态可为超空泡鱼雷动力学建模提供参考。

1 数学模型与求解方法

1.1 空泡截面扩展方程

其中初始条件为

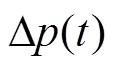
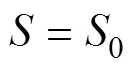
1.2 超空泡轴线的影响因素

1) 重力

Savechenko[7]给出的重力对空泡轴线的影响的近似公式为

应该说明的是重力影响下空泡轴线的偏移方向总是竖直向上的, 所以重力造成的偏移是基于地面坐标系的。

2) 空化器攻角

Logvinovich[8]利用摄动法给出了空化器攻角对空泡轴线影响的近似公式

3) 空化器侧滑角

空化器侧滑角的影响与空化器攻角的影响类似, 空化器侧滑角对空泡轴线影响的近似公式为

应该说明的是当雷体发生横滚时, 空化器攻角、侧滑角造成的偏移方向也会随之改变, 且总是垂直于弹道, 因此空化器攻角、侧滑角造成的偏移是基于速度坐标系的。

1.3 求解步骤

由于雷体运动轨迹基于地面坐标系, 因此文中根据独立膨胀原理计算的空泡形态也是基于地面系的。

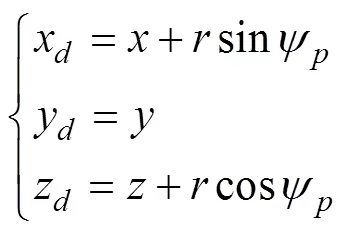
图2 空泡截面坐标示意图

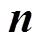
以上给出了某一空泡截面的各点坐标计算方法, 下面给出整个空泡表面各点坐标的详细求解步骤。

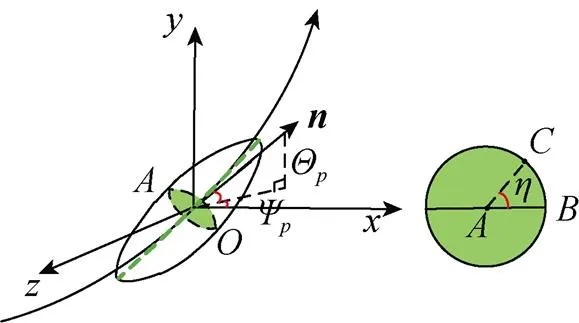
图3 空泡截面示意图

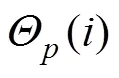
3) 空泡截面各点坐标的求解, 在已知偏移后轴线坐标及弹道偏角、弹道倾角的条件下, 根据式(11)求解截面上某一点的坐标, 由此点与式(12)可求解截面上各点坐标, 迭代空泡中轴线的各点坐标, 进而可求解出所有空泡截面各点的坐标。

应该说明的是在计算出所有空泡截面各点坐标后, 便可通过MATLAB等软件得到的三维空泡形态。

2 方法验证

2.1 与Logvinovich组合空泡模型的对比验证

Logvinovich组合空泡模型是基于独立膨胀原理的解析解, 该模型主要用于定常轴对称超空泡形态的预测, 适用于航行速度稳定且空化数较小的情况。Logvinovich组合空泡模型的表达式为[9]

Logvinovich组合空泡模型为半经验的空泡形态表达式, 对于定深直航运动的空泡形态计算有着较大优势, 但对于非定常运动下的超空泡航行体空泡形态计算就显得无能为力。运用文中方法与Logvinovich组合空泡模型计算直航下的三维空泡形态, 验证文中方法的正确性。

设空化器直径为0.042 m, 空化数为0.021, 不考虑各种因素对空泡形态的影响, 图4为文中方法和Logvinovich组合空泡模型仿真得到的空泡形态。

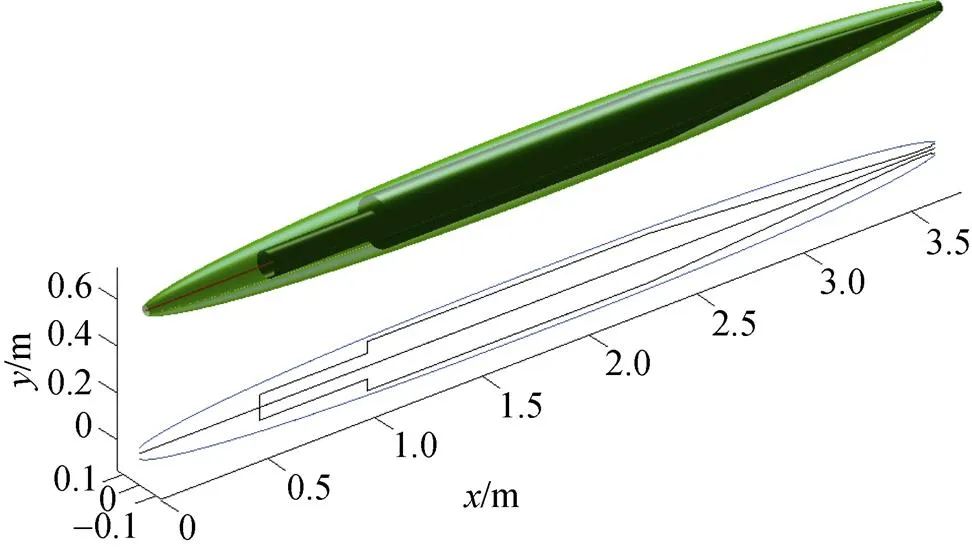
图4 文中方法与组合空泡模型仿真结果对比图

图中, 上侧空泡为文中方法仿真的结果, 下侧空泡为Logvinovich组合空泡模型仿真得到的结果, 两空泡长度与最大半径如表1所示, 可知两空泡尺度基本相同, 验证了方法的正确性, 且文中方法计算的是三维空泡形态, 得到的结果相对于Logvinovich模型信息更加全面。

表1 空泡尺寸对比

2.2 与CFD数值仿真方法仿真结果的对比验证

图5 时空泡形态

图6 时空泡形态

图中6(a)为CFD数值仿真的空泡形态, (b)为文中方法计算的空泡形态, 可知, 文中方法和CFD方法空泡形态吻合较好, 一定程度验证了文中方法的正确性。

3 三维超空泡形态仿真分析

对所建立的空泡形态模型进行仿真分析, 以说明文中方法可计算超空泡航行体在三维空间内沿任意轨迹变速、变深运动非定常状态下的三维超空泡形态。

3.1 小幅度变深运动空泡形态仿真分析

图7 变深运动三维空泡形态

表2 变深运动空泡尺寸

图8所示为此条件下空泡长度、最大半径、空化数与深度的变化曲线图。由图可知, 随着深度的线性增大, 空化数线性增大, 空泡长度、最大半径非线性减小, 且空泡长度、最大半径的变化率逐渐减小, 空泡最大半径的变化率大于空泡长度的变化率。

图8 深度变化时空化数、空泡尺寸变化曲线

3.2 变速运动空泡形态仿真分析

超空泡形态受航行速度的影响较大, 为了维持空泡形态的稳定, 超空泡鱼雷在巡航段一般保持速度不变航行, 然而由于外界环境与雷体实际航行中各种扰动的存在, 航行速度难免出现小幅度变化, 因此需要分析航行速度变化对超空泡形态的影响。如图9所示为空化器直径0.042 m、深度6 m、初始速度100 m/s条件下, 以加速度30 m/s2匀加速航行时, 在时刻0.037 4 s, 0.079 4 s, 0.121 4 s仿真得到的空泡形态。图中各空泡的长度和最大半径如表3所示, 由表可知, 随着航行速度的增大, 空泡的长度和最大半径都有所增大, 分析可知, 其机理是航行速度增大造成空化数减小, 从而使空泡尺寸减小。

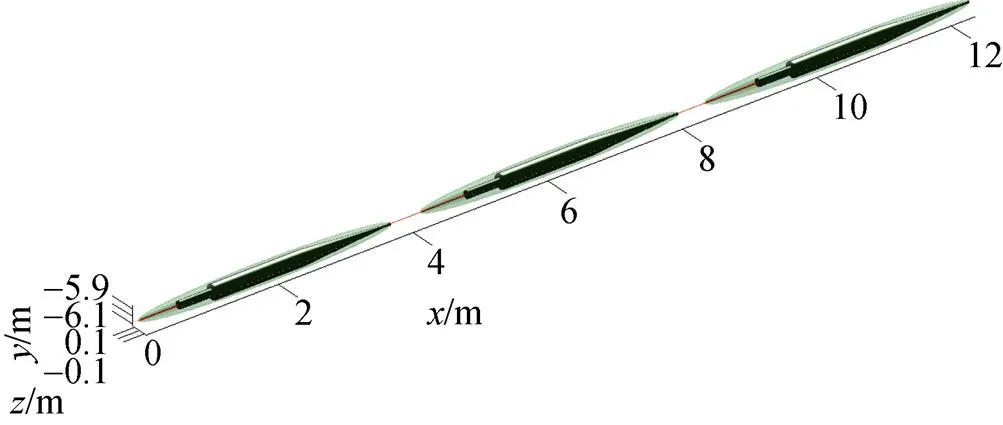
图9 变速运动三维空泡形态

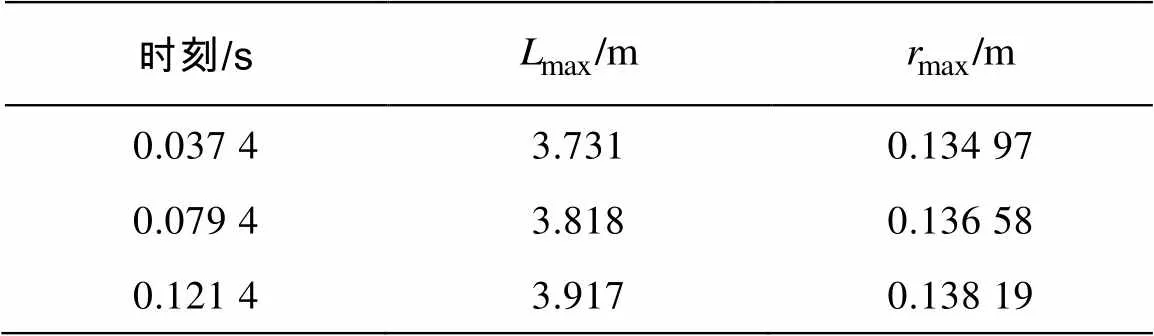
表3 变速运动空泡尺寸

图10所示为此条件下空泡长度、空泡最大半径和空化数与航行速度的变化曲线图。由图可知, 随着速度的线性增大, 空化数非线性减小, 空泡长度和最大半径非线性增大, 且空化数变化率逐渐减小, 空泡长度和最大半径变化率逐渐增大。

3.3 沿复杂轨迹运动的三维空泡形态仿真分析

常规水下航行体可进行较大幅度的变深运动, 而超空泡航行体因为空泡的约束, 深度只能在小范围内变化。该节将在小范围变深的前提下, 仿真计算超空泡航行体沿各种复杂轨迹运动的三维空泡形态, 以验证文中方法可适用于各种情况下的三维空泡形态仿真计算。

图10 匀加速航行空化数、空泡尺寸变化曲线

1) 纵平面小幅变深正弦轨迹运动

考虑重力效应的影响, 图11所示是速度为100 m/s时, 航行器在纵平面内沿周期为24 m、幅值为1 m的正弦轨迹运动三维空泡形态, 图中4个空泡的长度分别为3.48 m、3.28 m、3.20 m和3.28 m, 最大半径分别为0.132 2 m、0.129 3 m、0.128 8 m和0.131 0 m。可知仿真结果中4个空泡的尺寸先减小后增大, 这与深度变化造成空泡尺寸变化的理论结果一致。另外, 由于深度增大, 空泡尺寸减小, 雷体沿曲线运动, 空泡无法完全包裹雷体, 雷体的纵平面出现不对称沾湿。

图11 纵平面正弦轨迹三维空泡形态

2) 横平面正弦轨迹运动

考虑重力效应的影响, 图12所示的是在深度为6 m, 速度为100 m/s时, 航行器在横平面内沿周期为24 m, 幅值为1 m的正弦轨迹运动的三维空泡形态。由图可知, 与纵平面正弦轨迹运动类似, 超空泡鱼雷沿横平面正弦轨迹运动, 空泡也出现无法完全包裹雷体的情况, 雷体侧面出现不对称沾湿。

图12 横平面正弦轨迹三维空泡形态

3) 螺旋运动空泡形态仿真

考虑各种因素的影响, 在空化器直径0.042m、速度为100 m/s、初始深度6 m的条件下, 雷体在三维空间内沿70.17 m的回转半径作螺旋运动, 螺旋运动轨迹的特点是在雷体在横、纵平面内位置都发生了变化, 仿真计算的三维空泡形态如图13和图14所示。图中4个空泡长度分别为3.70 m、3.64 m、3.48 m和3.24 m, 最大半径分别为0.134 04 m、0.132 21 m、0.128 67 m和0.123 82 m。可知, 各空泡长度、最大半径逐渐减小, 这与航行深度增加, 外界压力增大, 从而使空化数增大、空泡尺度减小的理论结果是一致的, 一定程度上验证了仿真结果的正确性。

图13 螺旋运动轨迹三维空泡形态

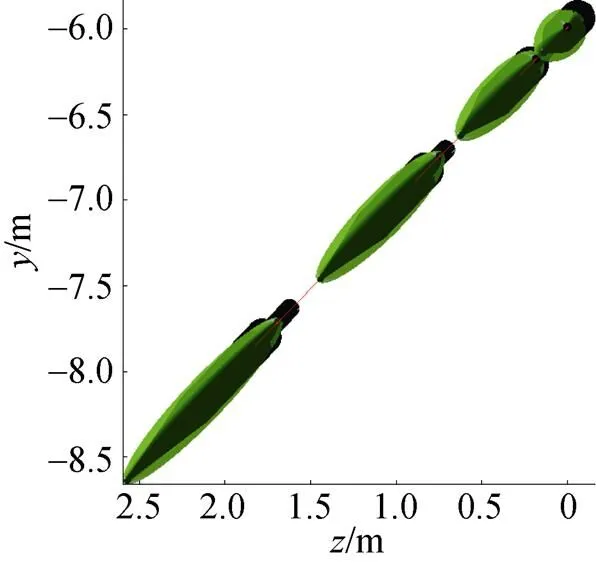
图14 螺旋运动轨迹三维空泡形态左视图

4 结束语

[1] 周景军, 董春鹏, 尹韶平, 等. 通气超空泡多相流场数值仿真方法[J]. 鱼雷技术, 2013, 21(3): 165-170.Zhou Jing-jun, Dong Chun-peng, Yin Shao-ping, et al. Numerical Simulation Method for Ventilated Supercavitating Multiphase Flow Field[J]. Torpedo Technology, 2013, 21(3): 165-170.

[2] Zou W, Yu K P, Wan X H. Research on the Gas-leakage Rate of Unsteady Ventilated Supercavity[J]. Journal of Hydrodynamics Ser B, 2010, 22(5): 778-783.

[3] 李魁彬, 王安稳, 施连会, 等. 基于Logvinovich原理射弹超空泡形态解析解研究[J]. 弹道学报, 2013, 25(1): 103-106.Li Kui-bin, Wang An-wen, Shi Lian-hui, et al. Researches on Analytical Solution of Projectile Supercavity Shaped Based on Logvinovich’s Principle[J]. Journal of Ballistics. 2013, 25(1): 103-106.

[4] 王改娣, 吕艳慧, 邹启明. 非定常人工通气超空泡数学仿真与分析[J]. 鱼雷技术, 2012, 20(5):321-325.Wang Gai-di, Lü Yan-hui, Zou Qi-ming. Mathematical Simulation of Unsteady Ventilated Supercavition[J]. Torpedo Technology, 2012, 20(5): 321-325.

[5] 张纪华, 张宇文, 李雨田. 内压扰动对非定常空泡形态的影响[J]. 弹道学报. 2012, 24(1): 88-92. Zhang Ji-hua, Zhang Yu-wen, Li Yu-tian. Effect of Internal Pressure Perturbation on Unsteady Cavity Form[J]. Journal of Ballistics, 2012, 24(1): 88-92.

[6] Semenenko V N. Dynamic Processes of Supercavitation and Computer Simulation[C]//MVKI Special Course on Supercavitating Flows. Brussels: RTO-AVT and VKI, 2001(12): 239-268.

[7] Savchenko Y N, Semenenko V N. Unsteady Supercavitation Motion of Bodies[J]. International Journal of Fluid Mechanics Research, 2002, 27(1): 109-137.

[8] Logvinovich G V, Buyvol V N, Dudko A S. Free Boundary Flows[M]. Kiev, Russian: Naukova Dumka Publishing House, 1985.

[9] Logvinovich G V. Hydrodynamics of Flows with Free Boundaries[M]. Kiev, Russian: Naukova Dumka Publishing House, 1969.

[10] Zhang Guang, Yu Kai-ping, Zhou Jing-jun. Numerical Research on Ventilated Supercavity Shape and Flow Structure in the Turning Motion[J]. Journal of Ship Mechanics, 2011, 15(12): 1335-1343.

A Calculation Method of Three-Dimensional Supercavity Shape Based on the Principle of Independent Expansion

SONG Shu-long1,2, WAN Ya-min1, LI Jian-chen1, ZHOU Jing-jun1, LÜ Rui1

(1. The 705 Research Institute, China Shipbuilding Industry Corporation, Xi’an 710077, China; 2. Science and Technology on Underwater Information and Control Laboratory, Xi’an 710077, China)

In view of the problem that the fluid dynamics calculation of supercavity torpedo maneuvering needs to accurately predict the three-dimensional supercavity shape in real time, a three-dimensional unsteady supercavity shape calculation method is presented based on the independent expansion principle of cavity section. The reasonability of the method is testified by comparing with the Logvinovich model and the computational fluid dynamics(CFD) numerical simulation method. The three-dimensional supercavity shapes of a torpedo in velocity-variable motion, depth-variable motion, horizontal-longitudinal plane motion along sinusoidal trajectory, and spiral motion in three-dimensional space are simulated and analyzed by the proposed method. Simulation results show that this method can predict three-dimensional unsteady supercavity shape of a torpedo moving along any trajectory. Compared with the Logvinovich model and the CFD numerical simulation method, this method can solve the three-dimensional supercavity shape with more comprehensive information and can save a large amount of computing resource. It is concluded that the present method can rapidly provide time-varying three-dimensional supercavity shape for engineering practice and provide a reference for the establishment of dynamic model of supercavity torpedo.

supercavity torpedo; independent expansion principle; three-dimensional supercavity shape; fluid dynamics

宋书龙, 万亚民, 李建辰, 等. 一种基于独立膨胀原理的三维超空泡形态计算方法[J]. 水下无人系统学报, 2019, 27(1): 51-58.

TJ631; O35

A

2096-3920(2019)01-0051-08

10.11993/j.issn.2096-3920.2019.01.009

2018-08-08;

2018-08-23.

宋书龙(1994-), 男, 在读硕士, 主要研究方向为流固耦合研究.

(责任编辑: 许 妍)