恒虚警检测信源数的方法
2022-02-16张一迪王悦斌王培志陆起涌张建秋
张一迪, 王悦斌, 王培志, 杨 沁, 陆起涌, 张建秋, 李 旦
(复旦大学信息科学与工程学院, 上海 200433)
0 引 言
在生物[1]、无线通信[2]、地球物理[3]、阵列[4]、金融[5-6]等诸多信号处理任务中,预先知道待处理信号源的个数(信源数)是许多信号处理算法的先验要求[7],如:参数化谱估计中的多信号分类(multiple signal classification,MUSIC)法[8-9]和信号参数估计的旋转不变性技术(estimate of signal parameters by rotational invariance techniques, ESPRIT)[10-11]、盲源分离中的独立元分析法[12]、信号降维[13]和/或特征提取中的主成分分析法[14]、参数化的时频分析法[15]等。
近几十年来,人们为这些信号处理算法发展出了一系列信源数检测的方法,纵观这些方法,不难发现它们不是基于信号观测的特征值或特征向量,就是基于描述信号信息的信息论[16]。发展于信息论的方法主要有:赤池信息准则[17-18](akaike information criterion,AIC)和最小描述长度[18-20](minimum description length,MDL)准则。这两个准则都发展于信号观测的对数似然函数,以及与待估计信源数有关的惩罚项。分析表明:AIC不是一个一致估计,即使在高信噪比(signal to noise ratio, SNR)的情况下,其结果的虚警率一直很高[21]。MDL准则虽然是一个一致估计,但其在低SNR或观测数量较少的情况下,给出的高漏报率是许多应用难以接受的[21]。此外,AIC和MDL方法对高斯白噪声这一假设,使得其在应对非高斯噪声时,性能变得非常差[21]。针对AIC和MDL存在的这些问题,人们通过利用不同的函数来替代对数似然函数和/或改进惩罚项,发展出了一系列基于信息论的新方法[22-26]。尽管这些新方法在噪声子空间中的特征值近似相等的情况下,效果较好;可是在当观测数据较小和/或SNR较低,以及噪声子空间中的特征值差异较大时,它们的性能都在一定程度上受到了破坏[27]。基于信号观测的特征向量,文献[4]和文献[28]报道了利用先验知识来检测信源数的新方法,不过其性能一直依赖先验知识是否有效[27]。
最近,文献[27]和文献[29]报道了通过寻找信号特征值或噪声子空间中的特征值来进行信源数估计的方法,认为降序排列的噪声子空间中的特征值近似服从指数分布,如此就可利用递归的方法估计出一个理想噪声子空间的特征值,当观测和理想噪声子空间特征值之差且与理想噪声子空间特征值之比大于某一阈值门限时,就认为该特征值是属于信号的,否则就是噪声的。该方法的主要缺点是:对于每一个特征值都需要采用蒙特卡罗方法计算出一个门限,文献[27]报道的一个在特征值的数量为5且虚警不超过0.01时的算例表明,计算出一个门限就需要进行16万次蒙特卡罗仿真,且这个计算量会随着特征值数量的增加而呈指数增加,如此大的计算量表明其应用价值十分有限。
针对非高斯噪声中信源数的探测问题,文献[21]报道了一种对高斯白噪声和非高斯噪声都有效的判别函数法,它试图利用降序排列特征值之间的斜率变化来区分信号和噪声子空间,不过本文的研究表明:在信源数远小于观测特征值数目时,估计的虚警率居高不下。基于信号观测特征值的二阶统计量(the second order statistic of eigenvalues,SORTE),文献[30]给出了一种新的信源数探测法,通过计算降序排列特征值两个相邻特征值之差的方差来估计信源数。相较于AIC和MDL,文献[30]的SORTE方法不需要估计参数来计算似然函数,而与文献[27]算法相比,SORTE的计算复杂度则低得多。本文将其与判别函数法进行的比较研究发现:虽然SORTE在信源数远小于观测特征值数量的情况时,其结果的虚警率低于判别函数法,但是当最小的几个特征值之差近似相等且都大于0时,它会将除最小的3个特征值以外的所有特征值都判断为信号的特征值,这意味着此时算法虚警率会高到难以满足应用的要求。
在目标检测中,许多应用都希望检测到假目标的概率能保持在一个可以接受的范围内。比如:在雷达和声呐的应用中,虚警率越高意味着检测到假目标的数量可能越多,而恒虚警检测则是指其中假目标所占的比例是固定的[31]。可是,文献中报道的信源数检测方法都不是恒虚警的,因此存在产生过高虚警率的可能性,这也就意味着其在满足雷达和/或声纳目标检测的应用要求时存在问题。针对存在的这一问题,本文提出了一种恒虚警检测信源数的方法,该方法首先将一个M×M阶观测协方差矩阵相邻特征值之差的统计量,定义成一个五维矢量序列,这样这个序列就有M-2个,利用K均值(K-means)聚类算法[32-35]将这M-2个五维矢量序列分成两类,并分别视其为信号和噪声两个子空间。当将噪声子空间中的特征值序列描述成一个统计分布,并通过期望最大(expectation maximization,EM)算法估计出这个统计分布时,奈曼-皮尔逊(Neyman-Pearson,NP)假设检验就可利用这个分布来对信源数进行恒虚警检测。考虑到EM算法估计统计分布和蒙特卡罗算法计算门限时计算复杂度过高,本文也给出了一个不管噪声子空间中的特征值服从何分布,且可大大降低计算复杂度的近似NP假设检验方法,这样就进一步简化了本文方法的计算并增强了它的实用性。数值仿真的结果在验证提出方法的有效性的同时,也优于其他方法。
1 问题描述
1.1 信号模型
在谱估计[36-37]、阵列信号处理[4]、雷达成像[38]、天文学[39-40]以及其他领域[41]中,信号的观测模型通常可以描述成如下线性模型[42]:
(1)
式中:y=[y1,y2,…yM]表示观测信号;ωk和sk为第k个信号分量的未知参数;a(·)是一个具有未知参数ωk的已知函数;K是未知的信源数;n为噪声。
重写式(1)为如下矩阵形式:
y=As+n
(2)
式中:A=[a(ω1),a(ω2),…,a(ωk)];s=[s1(t),s2(t),…sk(t)]T。此时,式(2)的协方差矩阵可以表示为[27]
Ry=E[yyH]=Rs+Rn
(3)
式中:E[·]表示期望运算。在无噪声的理想情况下,有Ry=Rs,也就是说信源数是观测信号y协方差矩阵Ry的秩,即K=rank(Ry)。而在应用中,由于噪声的存在,矩阵Ry一般是满秩的,因此信源数K≤rank(Ry),这意味着一般不能通过观测信号协方差矩阵的秩来确定信源数[27]。
在理想白噪声情况下,式(3)可以改写为[18,27]
Ry=ARsAH+σ2I
(4)
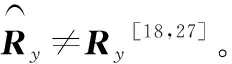
1.2 性能评价的标准
本文将用虚警率、漏报率、检测能力以及错误率来评价算法的性能。用K表示实际信源数,K*表示估计信源数,M表示观测数,这样虚警率、漏报率、检测能力以及错误率的定义以及计算方法就可以分别给出如下[35]。
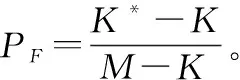
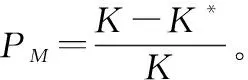
检测能力(PD)则表示信号特征值判别为信号的概率,计算公式为PD=1-PM。
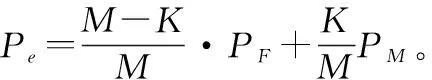
2 恒虚警的检测法
2.1 特征值筛选
为了区分式(3)中信号与噪声子空间中的特征值,本文首先定义一个由式(3)中相邻特征值之差统计量构成的五维矢量如下:
(10)
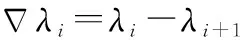
由文献[21]和文献[30]的分析可知,理论上相邻噪声子空间中的特征值之差近似相等且接近于0,而信号和噪声子空间中的特征值之差则较大。故当第i个特征值为噪声子空间中的特征值时,序列di中的5个统计量都应该近似等于0;而当其为信号特征值时,式(10)中的5个统计量都将大于0,这样视式(10)中不同di为不同的序列,那么就可利用K-means聚类算法将d=[d1,d2,…,dM-2]中的序列分为两类,并分别视它们为信号和噪声子空间。
令CN和CS分别表示噪声和信号子空间,μN和μs分别表示其所对应的聚类中心,则由如下K-means算法就可分别得到式(3)的噪声和信号子空间:
步骤 1选取聚类中心。与文献[30]的SORTE算法一样,本文假设最小的3个特征值是属于噪声的。因此,将dM-2作为噪声的聚类中心,记作μN;计算d与μN的欧氏距离,将与μN欧式距离最远的序列作为信号的聚类中心,即
(11)
步骤 2对数据进行聚类。对每一个序列Si计算D(di,μS)和D(di,μN),如果D(di,μS) 为了在给定虚警率的条件下检测信源数,就需要根据NP准则来设计判决门限δn,这样特征值中满足不等式λi≥δn的数量,就可视为给定虚警率的信源数[35]。通过NP准则来计算判别的门限,则需要知道噪声子空间中的特征值所服从分布的概率密度函数,而概率密度函数的高斯混合模型则可描述任一概率分布函数[43],因此假定式(3)噪声子空间中的特征值的概率密度函数可由如下高斯混合模型描述: (12) (13) 考虑到使用EM算法估计高斯混合模型的参数以及用蒙特卡罗方法计算门限时计算复杂度较高,因此,假设噪声子空间中的特征值是概率分布,都可由高斯分布近似。此时,近似的NP假设检验的判别门限为[35] δn=μN+Q-1(1-α)σN (14) 式中:μN和σN分别表示噪声子空间中特征值的均值和方差,Q-1表示正态分布累积分布函数的反函数。这样,就只需要计算噪声子空间中特征值的均值和方差就可以得到判别的门限。虽然这样处理大大减小了本文算法的计算复杂度,但是当噪声子空间中的特征值的概率分布偏离假设的高斯分布较大时,虚警率的误差会变大。即使如此,下面的仿真研究也表明:其性能依然优于文献最新报道的方法。 为了验证本文算法的有效性,本节进行了7组仿真实验,分别研究了提出算法控制虚警率的能力,检测能力、错误率和虚警率,及其与特征值的长度、SNR以及目标数量之间的关系,并将提出方法与文献中最新报道的算法进行了对比。为了后面描述方便,在不混淆的情况下,将用高斯混合模型描述噪声子空间中特征值的统计分布得到的算法作为本文算法;而本文近似算法则代表假设噪声子空间中特征值的统计分布是高斯分布,并用式(13)计算门限的算法。 第1组仿真实验,将研究本文算法控制虚警率的误差与信源数,以及噪声子空间中的特征值数N的关系,这里噪声子空间中的特征值数目与信号特征值数目之和简称为观测数。在仿真中,对高斯混合分布的混合个数,及其均值和方差的随机变化进行了1万次蒙特卡罗仿真,对其结果求均值得到的虚警率最大误差如图1所示。从图1中可以看出在噪声子空间中的特征值数量N≥30时,虚警率最大误差几乎不随信源数而改变。 第2组仿真实验将研究本文算法控制虚警率的误差与信源数以及SNR的关系。仿真中,在噪声子空间中的特征值数量为30的情况下对高斯混合分布的混合个数,以及它们均值和方差的随机变化的噪声进行了1万次蒙特卡罗仿真,对其结果求均值后得到的虚警率最大误差如图2所示。图2(a)的仿真实验结果表明,本文算法在SNR大于0 dB时,虚警率最大误差几乎不随信源数而改变。而图2(b)的仿真实验结果则表明,本章近似算法在SNR大于0 dB且不超过5 dB时,虚警率最大误差虽然随信源数的变化而有所改变,但其改变的数值较小。当SNR大于5 dB时,虚警率误差随SNR的增大而增加。这是因为随着SNR增大,噪声子空间中的特征值近似相等,此时其实际的统计分布与高斯分布相差较大。 第3组仿真实验研究了本文算法给定的虚警率与实际可达到的虚警率之间的误差,同时研究了高斯混合模型中高斯分布的个数c对其误差的影响。在仿真中,噪声子空间中的特征值数量设为30,在信源数随机变化的情况下,对高斯混合分布的混合个数,及其均值和方差的随机变化的噪声进行了1万次蒙特卡罗仿真,对其结果求均值后得到了表1的数据。从表1的数据中可以看出,本文算法控制虚警率的误差在±5%,且随着高斯混合模型中高斯分布数量的增加,虚警率误差呈减小趋势,当高斯分布个数大于等于5时,高斯分布个数对虚警率误差的影响几乎为0。 表1 本文算法达到的虚警率与高斯混合模型中高斯分布个数的关系 第4组仿真实验研究了本文算法给定的虚警率与实际可达到的虚警率之间的误差,同时研究了SNR对其误差的影响。在仿真中,噪声子空间中的特征值数量设为30,在信源数随机变化的情况下,对高斯混合分布的混合个数,及其均值和方差的随机变化的噪声进行了1万次蒙特卡罗仿真,对其结果求均值后得到了表2和表3的数据。从表2的数据中可以看出,当本文算法用高斯混合模型描述噪声子空间中的特征值的统计分布时,算法控制虚警率的误差在±5%,且SNR对虚警率的误差的影响可以忽略。而由表3的数据可知,当本文算法假设噪声子空间中的特征值服从高斯分布时,算法控制虚警率的误差会随着SNR的增加而变大。这是因为随着SNR的增加,噪声子空间中的特征值近似相等,此时其实际的统计分布与高斯分布相差较大。 表2 本文算法达到的虚警率与SNR的关系 表3 本文近似算法达到的虚警率与SNR的关系 第5组仿真实验将对判别函数法、SORTE算法、本文算法和本文近似算法,在不同信源数的情况下进行对比研究。在仿真中,观测数M=50,SNR为0 dB,虚警率给定为α=0.05。图3给出了这3种算法的虚警率、错误率和检测能力分别在10 000次蒙特卡罗仿真中的平均结果。 图3(a)仿真结果表明:SORTE算法的虚警率随着信源数的增加而有增大的趋势;判别函数法的虚警率随着信源数的增加而减小;本文算法与本文近似算法的虚警率几乎保持恒定,与给定的虚警率的误差不超过±5%。图3(b)表明:当信源数小于8时,本文算法及本文近似算法的错误率与SORTE算法相差不大,小于判别函数法;而当信源数大于8时,本文算法及本文近似算法的错误率小于SORTE算法,略高于判别函数法。但是在只有一个目标时,本文算法及本文近似算法的错误率远小于判别函数法。图3(c)当信源数小于15时,本文算法及本文近似算法的检测能力略差于判别函数法,好于SORTE算法;而当信源数大于15时,本文算法与本文近似算法的检测能力略好于判别函数法和SORTE算法。 第6组仿真实验将研究判别函数法、SORTE算法和本文算法与SNR的关系。在仿真中,观测数为35,信源数为3,其中包含2个大目标1个小目标,且小目标的幅度为大目标的-5 dB,虚警率给定为α=0.05。图4给出了这3种算法的虚警率、错误率和检测能力分别在10 000次蒙特卡罗仿真中的平均结果。图4(a)仿真结果表明:SNR对SORTE算法的虚警率影响几乎可以忽略;判别函数法的虚警率则随SNR的增加而减小;而本文算法与其近似算法的虚警率几乎保持恒定,与给定的虚警率的误差不超过±5%。图4(b)则表明:本文算法及本文近似算法的错误率小于判别函数法和SORTE算法。图4(c)则表明:本文算法及本文近似算法的检测能力好于SORTE算法,与判别函数法几乎一样。但由图4(b)可知,判别函数法的错误率是最高的;这是由于该算法在目标数量较少时虚警率过高造成的。 第7组仿真实验将研究判别函数法、SORTE算法和本文算法与观测数的关系。在仿真中,SNR为0 dB,信源数为5,其中包含3个大目标和2个小目标,且小目标的幅度分别为大目标的-5 dB和-10 dB,虚警率给定为α=0.05。图5给出了这3种算法的虚警率、错误率和检测能力分别在1万次蒙特卡罗仿真中的平均结果。图5(a)仿真结果表明:SORTE算法的虚警率随观测数增加而减小;判别函数法的虚警率随着观测数的增加而增加;本文算法与其近似算法的虚警率几乎保持恒定,与给定的虚警率的误差不超过±5%。同时,可以看出随着观测数增加,本文算法及本文近似算法控制虚警率的误差变小。图5(b)表明:本文算法及本文近似算法的错误率小于判别函数法和SORTE算法。图5(c)则表明:当目标数量较少且含有小目标时,判别函数法的检测能力最好,但由图5(b)可知,此时该种算法的错误率是最高的,这是由于其虚警率较高而导致的;SORTE算法则只能检测出3个大目标。而本文算法及本文近似算法的检测能力则好于SORTE算法,略低于判别函数法。需要强调的是,本文算法及本文近似算法的虚警率是最低的,且控制虚警率误差的能力最好,这就意味着其可以通过提高虚警率来提高本文算法的检测能力。 针对目前已有的信源数检测算法不能控制虚警率的问题,本文提出了一种恒虚警检测信源数的方法。该方法利用本文定义的观测信号协方差矩阵相邻特征值之差统计量所构成的五维矢量序列,可利用K-means聚类算法将其分成两类。当分别视其为信号和噪声两个子空间,且将噪声子空间对应的特征值序列描述成一个统计分布,并通过EM算法估计出这个统计分布时,NP假设检验就可利用这个分布来对信源数进行恒虚警检测。为了提高算法效率和实用性,本文也给出了一种可大大降低计算复杂度的近似奈曼-皮尔逊假设检验方法。数值仿真的结果在验证提出方法的有效性的同时,也表明其性能优于判别函数法和SORTE算法。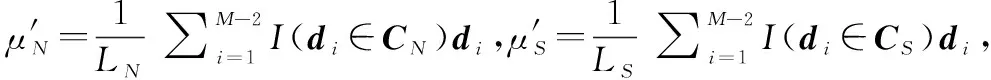
2.2 门限计算
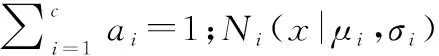

3 仿真实验



4 结 论
