基于逆高斯退化过程的面向任务系统CBM优化模型

陈云翔, 李京峰,*, 项华春, 李恒年

(1. 空军工程大学装备管理与无人机工程学院, 陕西 西安 710051;2. 西安卫星测控中心宇航动力学国家重点实验室, 陕西 西安 710043)

0 引 言

航空航天、工业制造等领域的关键系统在执行任务期间往往会伴随性能退化现象,且一些系统的性能退化过程单调不可逆。如果关键系统在任务阶段发生故障,不仅会造成严重的经济损失,还会阻碍任务进程。为确保关键系统安全可靠运行,随着检测技术的不断发展,视情维修(condition-based maintenance, CBM)作为一种有效手段已受到学者广泛关注。它可根据具备检测条件的关键系统的退化状态信息及预设阈值,决定系统是否需要维修或更换。

根据修复程度的不同,维修通常可分为3类,即完全维修、不完全维修和小修。然而在工程实际中,关键系统的结构较为复杂,对其实施的维修活动多为不完全维修,系统只能恢复到“如新”和“如旧”之间的某一状态。因此,一些学者开始在退化系统的CBM优化研究中考虑不完全维修的影响。葛恩顺等在基于Gamma过程建立的退化系统CBM模型中,引入了不完全维修对系统退化状态的影响,该影响会随着工作时间的延长和维修次数的增多而加重。Guo等基于Wiener过程研究任务导向型系统的CBM优化模型时,利用指数分布刻画了不完全维修对剩余退化量的影响。Do等提出一种自适应CBM优化模型,在深入分析不完全维修正面和负面影响的过程后,认为不完全维修对退化量的恢复程度是随机的。刘葛辉等在不完全检修计划优化模型中,通过役龄回退因子描述不完全维修对系统寿命的影响。Zhang等则从退化率的角度，利用随机改进因子描述了不完全维修的效果。以上研究虽然在考虑不完全维修的维修策略优化中取得一定效果,但是忽略了不完全维修对退化量和退化率均会产生影响的事实。因此在不完全维修建模时必须将两类影响考虑在内。

另一方面,系统进行更换的时机一般包括系统故障或系统运行时间达到预定服役年限两种情况。但对于关键系统,为提高任务成功概率,其更换时机还应考虑任务要求的可用度约束,当系统在寿命周期的某一阶段无法满足规定可用度时,需要进行预防性更换。因此,可用度约束会对维修优化过程产生影响,其在建模时不可忽略。例如:Zhou等在基于连续状态部分可观测半马尔可夫决策过程的维修策略优化模型中,考虑了可用度约束对目标函数的影响。Barone等在制定桥梁结构的最优维修计划时,将可用度、风险等纳入成本目标函数中,通过遗传算法进行多目标优化。Do等则将维修策略优化模型进一步扩展到多部件串联系统中,同时在可用度和有限维修人员约束条件下给出了用于维修决策的启发式优化方案。然而,以上研究尚未结合不完全维修影响。为解决此类问题,Shen等针对动态环境中具有不同退化过程的系统建立了维修策略优化模型,该模型考虑了不完全维修造成的剩余损伤,以及求解过程会受到可用度和系统运行时间约束。苏春等建立了可用度约束下的风力机单部件顺序维修优化模型,同时考虑了不完全维修对有效年龄的影响。但是二者仅从退化量的角度刻画了不完全维修影响,尚未把不完全维修对退化率的影响融入到模型当中。

可以发现,现有文献中少有模型将不完全维修的双重影响和任务要求的可用度约束同时整合到CBM优化中。因此,本文针对具有单调退化过程的关键系统,基于单次任务后的定期检测策略,提出一种考虑不完全维修双重影响与可用度约束的CBM优化模型。具体方法为:建立具有随机漂移系数的逆高斯过程退化模型,在首达时间的意义下推导出相关函数的解析概率分布;分析系统演化过程,得到不完全维修对退化量和退化率的影响;结合可用度约束给出系统进行维修或在不同时机更换的概率公式,并以长期运行期望费用率为目标构建CBM优化模型;最后通过数值实验对本文构建模型验证和对比,并进行参数敏感性分析。

1 基于逆高斯过程的退化模型

Wasan提出的逆高斯过程作为一种连续时间连续状态的单调随机过程,不仅能够描述系统退化随时间单调增加的特征,而且在引入随机效应方面具有优势。因此,本文在逆高斯过程的基础上进行扩展和建模。

1.1 具有随机漂移系数的逆高斯过程

令()表示时刻的系统退化状态,假设退化过程{(),≥0}服从逆高斯过程,即()～IG((),[()]),其中、分别表示逆高斯过程的漂移系数和扩散系数,反映退化过程的速率和波动。()表示时间尺度函数且单调递增,按照约定,(0)=0。

考虑到系统退化状态通常具有在运行初期不确定性较大,随着运行时间的延长逐渐趋于平稳的特点。本文将随机漂移系数融入到逆高斯过程并使用()=的线性形式进行描述。具体如下:

(1)

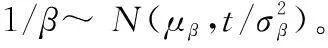
1.2 相关概率分布

基于首达时间的概念,设预防性维修阈值为,故障阈值为,将零时刻起系统首次达到和的时间分别定义为

=inf{|()≥,≥0}

(2)

=inf{|()≥,≥0}

(3)

根据逆高斯过程的单调性,当为固定值时,得到的条件分布函数为

(4)

式中：(·)表示逆高斯分布的条件分布函数;(·)表示标准正态分布的分布函数。通过对求导,得到的条件概率密度函数为

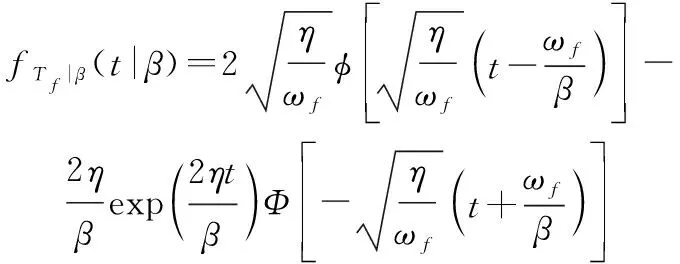
(5)

式中：(·)表示标准正态分布的概率密度函数。

上述|(|)为关于的条件分布函数,根据全概率公式可以得到

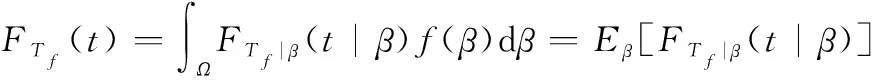
(6)

式中：()、和[·]分别表示随机效应参数的概率密度函数、参数空间和数学期望。为计算式(6)积分的解析表达式,需根据文献[28]中的引理1进行推导。

如果～(,),且,,∈,则以下结果成立:

(7)

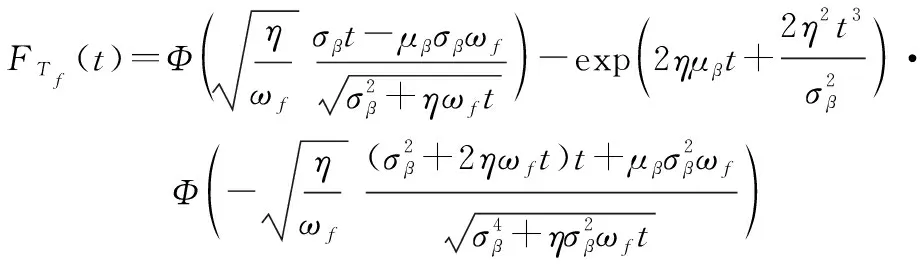
(8)

利用式(8)对求导,可得()的表达式为

(9)

同时,根据式(8)可进一步反向推导得到退化过程{(),≥0}的分布函数为

(10)

进一步对求导,可得退化过程{(),≥0}的概率密度函数为

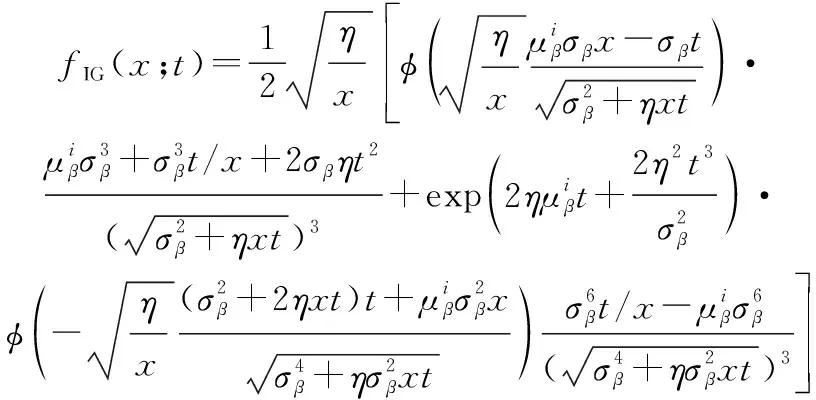
(11)

由式(11)得到了系统的寿命分布函数。令0:={,,…,}表示在0=<<…<时刻获取的退化数据,其中=()表示时刻系统的退化状态。基于故障阈值,将系统在时刻的剩余寿命定义为

=inf{|(+)≥,≥0}

(12)

根据独立增量性质和齐次马尔可夫性质,得到

=inf{|(+)≥,≥0}=
inf{|(+)-()≥-,≥0}=
inf{|()≥-,≥0}

(13)

然后,利用式(13)的结论可直接得到

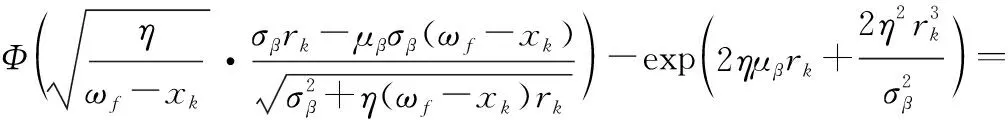
(14)

2 系统演化过程及影响分析

2.1 假设条件

(1) 假设每次任务持续时间是一个大于0的固定常数,用表示。在任务结束时,系统被完全检测,并产生一个固定成本,检测时间忽略不计。

(2) 如果在执行任务期间,系统发生故障导致任务失败,或者在任务结束时检测到系统状态满足()≥,则立即进行故障后更换,以使系统恢复如新,产生固定成本。

(3) 如果当任务结束时，≤()<,且满足任务要求的可用度约束,则在下一个任务之前立即进行预防性维修,维修时间不可忽略,维修的单位时间成本为。

(4) 维修是不完全的,只能将系统恢复到“如新”和“如旧”之间的某一状态,且对退化量和退化率均有影响。

(5) 如果当任务结束时满足≤()<,但违反任务要求的可用度约束,将进行预防性更换以使系统恢复如新,并产生固定成本。

(6) 如果当任务结束时()<,系统继续运行,不采取任何操作。

(7) 当系统运行时间达到时,亦将进行预防性更换,产生固定成本,其中∈表示系统可以执行的最大任务数。

(8) 所有更换活动(包括故障后更换和两种预防性更换)都消耗相同的时间。

2.2 系统演化过程描述

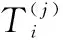
图1 系统演化过程Fig.1 The system evolution process

对于单调退化系统而言,其性能会在执行任务期间逐渐退化,通过检测手段可以获取系统当前退化状态,从而指导维修和更换活动。其中包括的逻辑关系可描述如下:① 若系统在任务期间突发故障,则立即进行故障后更换;② 若系统正常运行至任务结束,首先判断运行时间是否达到,若达到则进行预防性更换,若没有达到再进行检测;③ 根据检测结果,首先判断系统状态是否满足()≥,若满足则进行故障后更换,若不满足则进入下一步;④ 判断系统状态是否满足()≥,若不满足则系统继续运行,不采取任何操作,若满足则进入下一步;⑤ 判断当前预防性维修周期的可用度是否满足约束条件,若满足则进行预防性维修,否则进行预防性更换。逻辑关系图如图2所示。

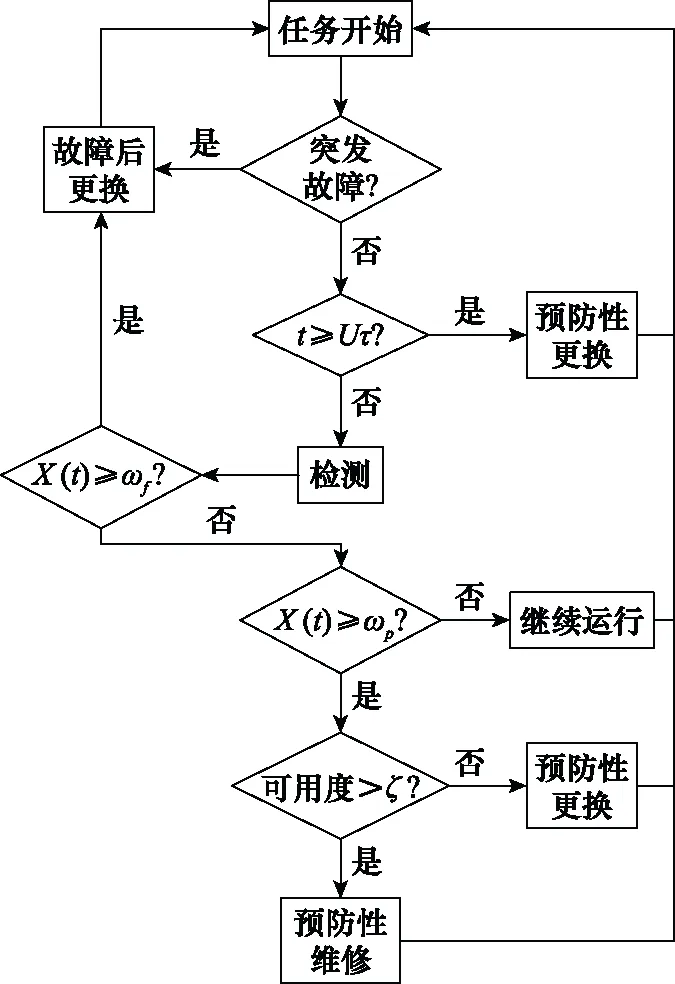
图2 系统维修和更换逻辑关系Fig.2 Logical relationship between system maintenance and replacement

2.3 预防性维修持续时间模型

一般来说,系统维修后恢复程度会随着维修次数的增多和预防性维修阈值的延长呈现递减趋势,使得寿命周期内的维修时间逐渐增加。为刻画这一特点,令表示第次预防性维修所需时间,对任意≠,独立于。基于文献[31]中关于的期望模型,本文提出一种关于预防性维修次数和预防性维修阈值的改进模型,公式如下:

E[]=exp()

(15)

式中：>0,≥0,=1,2,…且=0,假设参数和与无关。可以发现,的期望值随着预防性维修阈值和维修次数的增加而增加,改进结果更加符合实际。

2.4 不完全维修的影响

在工程实际当中,对系统进行不完全维修对退化量和退化率均会产生影响,具体可表现为维修后仍有剩余损伤且随机漂移系数改变,下面分别进行讨论。

(1) 剩余损伤

观察图1可知,在每次不完全维修过后,系统的初始退化状态将从某个非零值(比如、)开始且逐渐增加(>),直到进行更换才重新归零。和被称为剩余损伤,它将缩短预防性维修间隔时间。依据文献[12]提出的剩余损伤模型,得到剩余损伤的概率密度函数为

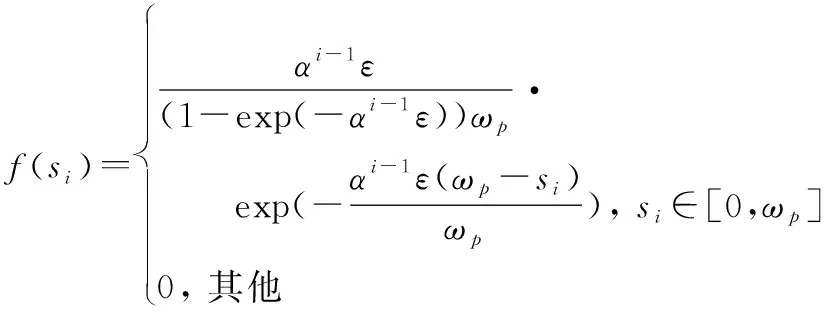
(16)

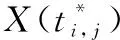
因此,的数学期望E[]为

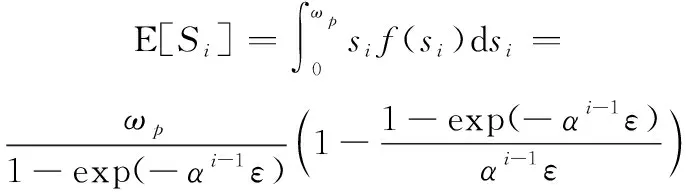
(17)

可以证明,E[]会随着维修次数单调递增。因此,剩余损伤的存在导致每个寿命周期内的任务数都是有限的。

(2) 随机漂移系数

由于本文采取了式(1)描述的随机漂移系数,所以认为不完全维修对退化率的影响体现在随机漂移系数的参数上,即每次维修过后都会产生一个关于的更新因子。因此的更新公式为

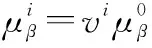
(18)

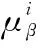
3 CBM优化模型

3.1 可用度约束

令A1[]表示每个寿命周期中第个预防性维修周期的可用度,其中第个预防性维修周期由第个预防性维修间隔时间和第-1个预防性维修持续时间组成。A1[]的表达式如下:

(19)

其中

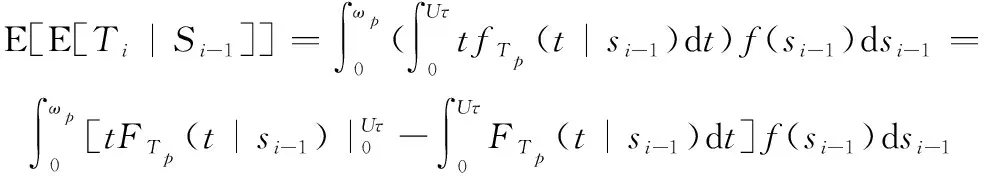
(20)

根据式(8)和式(14),可得

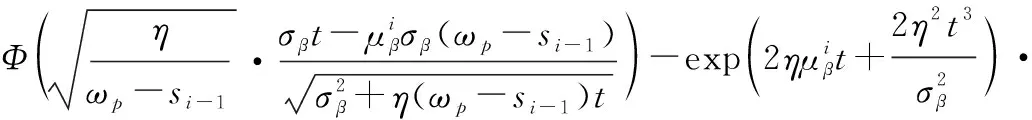
(21)

由假设条件(7)可得,如果系统在寿命周期内的可用度A1[]降低到任务要求的约束水平,则将进行预防性更换使系统恢复如新。

3.2 预防性维修概率模型

如果在第个预防性维修周期内,系统状态满足((-1))<且≤()<,则在第次任务后将进行预防性维修。该事件在剩余损伤为-1条件下发生的概率为

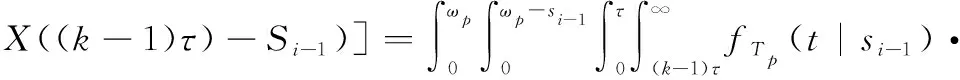
(22)

关于-(;|-1)和-(;|-1)的表达式,只需将式(21)中的(--1)分别替换为(---1)和(---1)即可,这里不再具体展示。

3.3 3种更换概率模型

如前所述,系统进行更换的时机有3种:一是故障后更换,二是系统运行时间达到进行预防性更换,三是由于可用度约束进行预防性更换。下面分别进行讨论。

(1) 系统故障

假设系统在进行故障后更换之前有(=1,2,…)个预防性维修周期,∈表示第个预防性维修周期的任务数。在第+1个预防性维修周期的((+1-1),+1]区间内系统随机发生故障。此外,系统故障前还需满足可用度约束,即每个预防性维修周期的A1[]>。基于式(22),给定组合,…,+1发生故障后更换的概率为

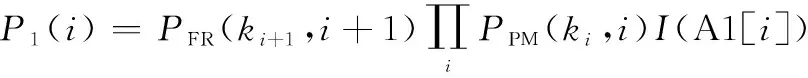
(23)

式中：(+1,+1)为在第+1个预防性维修周期的((+1-1),+1]区间内发生故障的概率,(A1[])为示性函数,二者表达式分别是

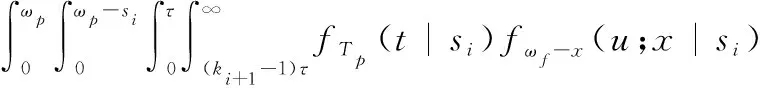
(24)

(25)

特别地,当=0时,即系统故障前未进行过维修,(0)=(,1)。

由此可得该情形下的期望运行时间E[]、期望停机时间E[]、期望成本E[]分别为

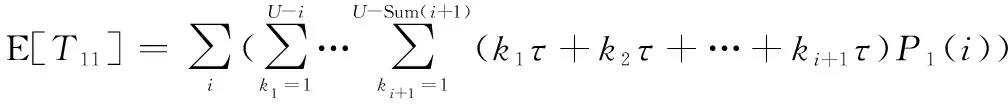
(26)

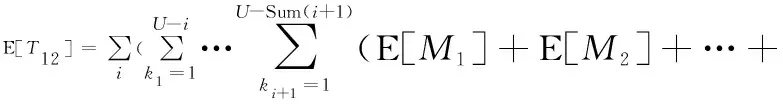
(27)

E[]++…++1-+)())

(28)

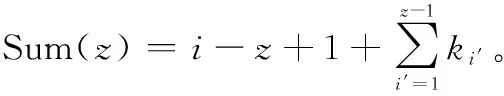
(2) 系统运行时间达到

类似于故障后更换中的假设,系统在第+1个预防性维修周期执行任务数达到,然后进行预防性更换。同样在前个预防性维修周期,满足A1[]>。基于给定组合,,…,+1,该预防性更换发生的概率为

(29)

特别地,当=0时,即系统执行任务数达到时未进行过维修,此种情形发生的概率为

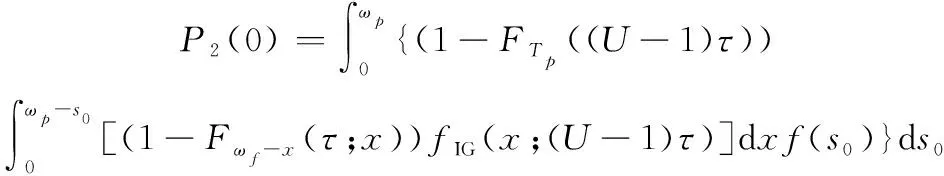
(30)

由此可得该情形下的期望运行时间E[]、期望停机时间E[]、期望成本E[]分别为

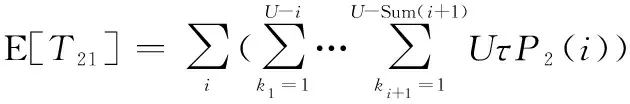
(31)

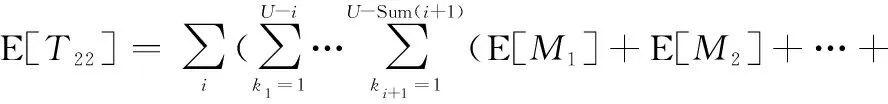
(32)

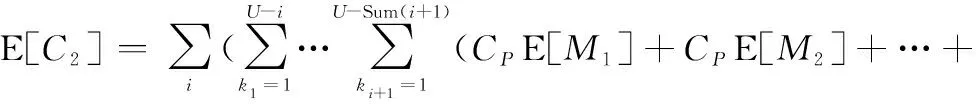
(33)

(3) 系统达到可用度约束

参照前2种假设,系统在运行到之前由于可用度约束进行预防性更换。在前个预防性维修周期,系统运行状态均满足A1[]>,然而在第+1个预防性维修间隔时间结束时,A1[+1]≤。需要说明的是,当=0时,由于A1[1]=1,系统不会由于可用度约束进行预防性更换。因此,基于给定组合,,…,+1,该预防性更换发生的概率为

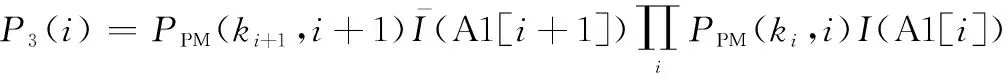
(34)

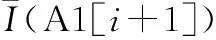
由此可得该情形下的期望运行时间E[]、期望停机时间E[]、期望成本E[]分别为

(35)

(36)

(37)

3.4 优化模型

为解决考虑不完全维修双重影响与可用度约束的单调退化系统CBM优化问题,本文以最小化长期运行期望费用率为目标,决策变量为预防性维修阈值。根据更新报酬理论,CBM优化模型表示为

(38)

式中：E[]=E[]+E[];E[]=E[]+E[];E[]=E[]+E[]。

4 数值实验

本节通过数值实验对上述优化模型进行验证,得到目标函数的最优解及相关决策变量。然后,将本文提出模型(以下简称模型1)与仅考虑不完全维修对退化量影响的模型(以下简称模型2)进行对比。最后对模型参数进行敏感性分析。

4.1 参数设置

4.2 实验结果及对比分析

(1) 实验结果

由于剩余损伤和预防性维修持续时间会随维修次数的增加而增加,导致系统总会由于可用度约束而进行预防性更换。因此,预防性维修周期数通过实验可以得到一个上限,以简化计算过程,实验结果如图3所示。

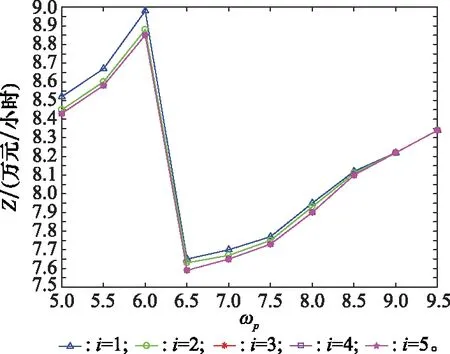
图3 预防性维修周期上限实验结果Fig.3 Experimental results of upper limit of the preventive maintenance cycle

观察图3可知,当>3时,不同对应的长期运行期望费用率均一致,因此,预防性维修周期上限=3。值得注意的是,当>85时,不同预防性维修周期数对应的长期运行期望费用率几乎一致。这是因为寿命周期中具有多个预防性维修周期的概率随着的增加而减少,导致不同预防性维修周期数对应的费用差异逐渐缩小。

同时,根据图3中优化算法对决策变量的搜索结果来看,当=65时,长期运行期望费用率达到最小,最小值为759万元小时,此时得到系统的最优维修策略(=65)。

(2) 对比分析

为了验证综合考虑不完全维修对退化量和退化率的影响在维修优化中的作用,现将模型1与模型2进行对比。模型2的实验参数设置与模型1相同,实验结果如图4所示。

图4 模型1与模型2对比结果Fig.4 Comparison results of model 1 and model 2

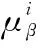
4.3 敏感性分析

为进一步验证模型参数对系统维修费用和策略的影响,本文将模型参数大体分为2类,运用控制变量法分别从退化特性、可用度约束两方面进行敏感性分析。

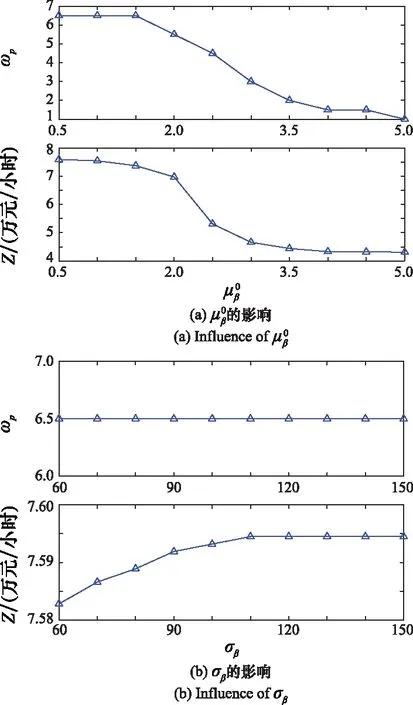
图5 和σβ对最优维修费用和策略的影响Fig.5 Influence of and σβ on optimal maintenance cost and policy

接着对可用度约束参数进行讨论,研究对象为,变化范围满足085≤≤099,其余参数固定不变,实验结果如图6所示。

图6 ζ对最优维修费用和策略的影响Fig.6 Influence of ζ on optimal maintenance cost and policy

观察图6可以发现,当从085增加到099时,最优长期运行期望费用率从1032万元小时减少至668万元小时,相应地，最优预防性维修阈值从95减少至15,且在[085,091]区间时,费用率和预防性维修阈值分别保持1032万元小时和95不变。造成此现象的主要原因是开始可用度设置略低,导致整个系统演化过程中第3种更换发生次数固定甚至没有发生,从而使最优解没有发生变化。之后最优长期运行期望费用率和预防性维修阈值变小,是因为可用度的增加使得部分第一种更换变成第3种,而预防性更换的成本比故障后更换的成本要低,因此维修费用会逐渐减少。同时,可用度要求越高,最优预防性维修阈值只有降低才能使得系统在寿命周期内尽可能多地进行成本较低的预防性维修活动,而不是由于可用度约束直接进行代价更高的预防性更换。

5 结 论

本文针对现有CBM优化模型中不完全维修影响考虑单一,且未同时融入可用度约束的问题,提出了一种同时考虑不完全维修双重影响和可用度约束的单调退化系统CBM优化模型,给出了系统长期运行期望费用率的解析计算方法。通过数值实验验证了所提模型的可行性,与模型2的对比结果显示出本文模型具有更优的经济性,进而证明了考虑不完全维修双重影响的必要性。此外,关于系统退化特性和可用度约束的敏感性分析结果表明,可用度约束参数对CBM优化结果的影响比退化特性参数更加明显。