基于全局最优和差分变异的头脑风暴优化算法

马威强, 高永琪, 赵 苗

(海军工程大学兵器工程学院, 湖北 武汉 430033)

0 引 言

群体智能优化算法通过个体间信息共享、合作、竞争等一系列规则,实现群体走向解决方案搜索空间中越来越好的领域。传统的群体智能优化算法如粒子群优化(particle swarm optimization, PSO)算法、蚁群优化(ant colony optimization, ACO)算法、野草入侵优化(invasive weeds optimization, IWO)算法等,多受到生物行为的启发,而人是世界上最聪明的群居生物,受人类创造性问题求解过程启发的头脑风暴优化(brain storm optimization,BSO)算法可以认为是一种很有潜力的算法。

近年来,BSO作为一种新的群体智能优化算法,引起了众多学者的广泛关注,BSO及其改进型已在一些领域得到成功应用,如卫星编队优化、直流无刷电机优化、无线传感器网络、Wiener模型参数辨识、图像处理、航路规划等等。在BSO的基础上,国内外学者围绕其聚类、选择、变异等方式衍生出不同的BSO算法,提高了算法性能。Zhan等人用一种简单的聚类方法(simple group method, SGM)代替原BSO中的K-means聚类,并用差分变异代替高斯变异,以缩短运行时间和提高寻优精度,但多次寻优结果的离散程度较大。Zhu等人提出使用k-medians算法进行聚类,避免K-means聚类中异常值所带来的弱点,同时提高算法运算速度,但在部分多峰函数中的寻优精度不高。El-abd等人提出基于适应度的分组方法,按维度更新,并遵循全局最优思想寻优,提高了寻优精度,但收敛速度较慢。本文采用追随全局最优策略和差分变异策略,提出了一种改进的BSO算法,以提高算法寻优精度,加快算法收敛速度。

1 BSO算法

初始种群随机给出,其个体散乱分布在整个搜索空间。BSO通过聚类、取代、选择、变异等操作产生新个体,优胜劣汰,从而一代代改进个体,实现全局优化,得到更优解。

聚类操作采取K-means策略,并定义每一类的最优个体为该类的类中心。聚类后,以一定概率产生随机个体取代某一个类的类中心,防止算法过早地收敛,并有助于算法跳出局部最优。

BSO有以下4种方法选择待变异个体:① 按照轮盘赌概率选中一个类,选择该类的类中心为待变异个体;② 按照轮盘赌概率选中一个类,选择该类中随机一个个体为待变异个体;③ 随机选中两个类,融合两个类的类中心成为待变异个体;④ 随机选中两个类,在两个类中各随机选出一个个体,融合成为待变异个体。

选择操作中的融合过程按如下表达式进行:

=r+(1-)

(1)

式中:是两个个体融合后产生的待变异个体;与是接受融合的两个个体;是一个0到1的随机数,调节两个个体的权重。

变异操作将在待变异个体上加扰动量,本文称该扰动量为变异步长,高斯变异按如下表达式进行:

=+·(,)

(2)

式中:是新个体的第维;是待变异个体的第维;(,)是以为均值、以为方差的高斯随机数;变异系数的计算公式如下:

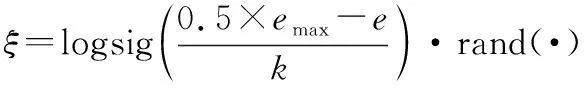
(3)

式中:是最大迭代次数;是当前迭代次数;是调节型传输函数logsig坡度的系数;rand(·)是0到1之间的随机数。

2 基于全局最优和差分变异的BSO算法

本文采用追随全局最优策略,在更新个体过程中充分利用全局最优信息,并用差分变异代替原来的高斯变异以自适应调节变异步长,不仅提高了寻优精度,而且加快了运算速度。

2.1 追随全局最优策略

在PSO算法中提出的追随全局最优策略,在许多算法中得到应用。本文将追随全局最优策略引入BSO,原个体通过追随全局最优个体产生新个体。BSO在选择待变异操作个体时,有一定概率采用选择类中心的方法,实际上就是选择类的最优个体,可以不再考虑追随全局最优;若不采用选择类中心的方法,让选择出来的个体追随全局最优。追随全局最优策略如下:

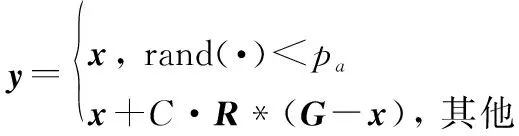
(4)

式中:是全局最优个体;是一个维的向量,其每一维为0到1的随机数;是全局最优影响系数;是通过类中心确定待变异个体的概率,可表示为

=·+(1-)·

(5)

式中:为通过一个类选择个体的概率;为选择一个类后选择类中心的概率;为选择两个类后选择类中心融合的概率。

进行最优个体的搜索时,搜索初期的个体随机性较大,全局最优个体质量可能不高,追随全局最优的意义较小,不必太大。随着搜索的进行,个体质量整体上升,全局最优个体质量提高,追随全局最优的意义变大,应该随之增大。令随迭代次数递增,表达式如下:

(6)

式中:与是系数的边界值。

2.2 差分变异策略

搜索初期应该进行全局搜索,到后期由于个体质量的整体上升,应重点进行局部搜索,因此算法前期变异步长应该比较大,后期变异步长比较小。BSO采取高斯变异,变异系数由logsig函数确定,变化趋势如图1所示。

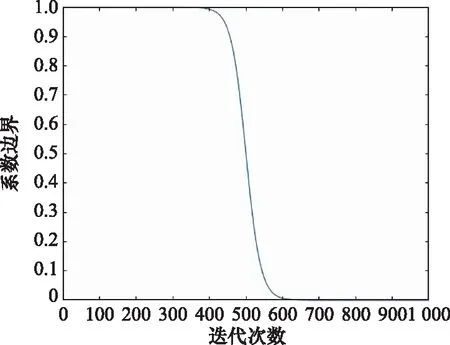
图1 高斯变异系数变化趋势Fig.1 Variation trend of Gauss mutation coefficient

在算法搜索前期,变异系数比较大,后期变异系数比较小,符合前期变异步长大,后期变异步长小的需求。但一旦最大迭代次数确定,高斯变异系数变化趋势就固定了,变异系数未考虑到种群自身情况,算法不能很好地捕捉搜索特征,而不同优化问题的搜索特征往往是不一样的。

在人类头脑风暴过程中,前期每个人的想法都会有很大差异。在创造新观念时,要考虑到现有观念的差异。因此,本文通过差分变异来确定变异步长。基于差分变异的变异操作如下所示:

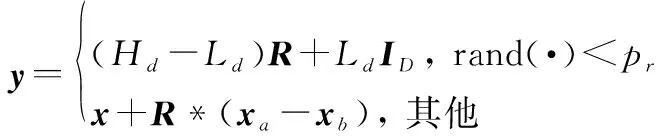
(7)

式中:与是搜索空间的边界值;表示有一定概率得到一个随机新个体;*表示哈达马积；与是种群中的任意两个不同个体。

差分变异相对于高斯变异有两方面的优势。一方面,高斯变异的运算包括logsig函数、高斯分布函数、随机函数和四则混合运算,而差分变异仅有随机函数和四则混合运算,运算量大大减少。另一方面,差分变异的变异步长基于当代种群而来,根据种群个体的离散程度进行自适应调节:在种群分散时有较大的变异步长,在种群集中时有较小的变异步长。变异步长根据种群反馈情况来实时确认,算法能较好捕捉搜索特征。

3 仿真研究

利用6个标准测试函数(如表1所示),从3、10、30、50维度来研究基于全局最优和差分变异的BSO(global-best difference-mutation brain storm optimization，GDBSO)算法,这里的维度是指自变量的个数。为每个标准测试函数设置一个可接受解,其中,Griewank、Rastrigin函数的可接受解为1.00E-02,其他函数的可接受解为1.00E-10。首先研究参数设置对GDBSO性能的影响,给出参数设置建议范围;随后对BSO、改良BSO(modified BSO,MBSO)算法、全局最优BSO(global-best BSO,GBSO)算法与GDBSO进行仿真对比研究,检验分析算法性能。每一组仿真都独立运行50次。计算机仿真平台为Matlab 2016a,处理器为Inter(R) Core(TM)i5-6200U CPU@2.30GHZ,RAM4GB,操作系统为Windows10-64位。

表1 选取的标准测试函数

3.1 参数选择

参考文献[2]中BSO算法共同参数设置为:种群规模=100、聚类数目=5、取代操作执行概率=02、=08、=04、=05。文献[11]指出,与的选取对算法性能影响不大,取=08,=02。最大函数评估次数为=×10,为维度。取为0、0001、0005、001、005、01进行仿真,3维度、30维度下的寻优结果如表2和表3所示。

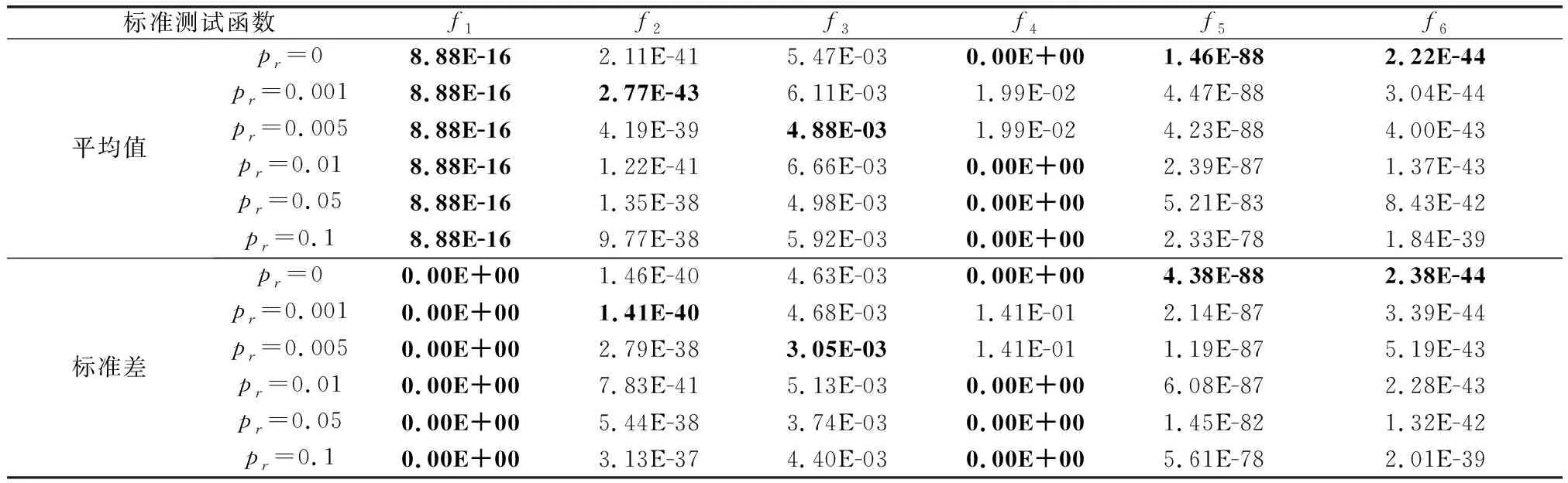
表2 GDBSO设置不同参数在3维度下寻优结果

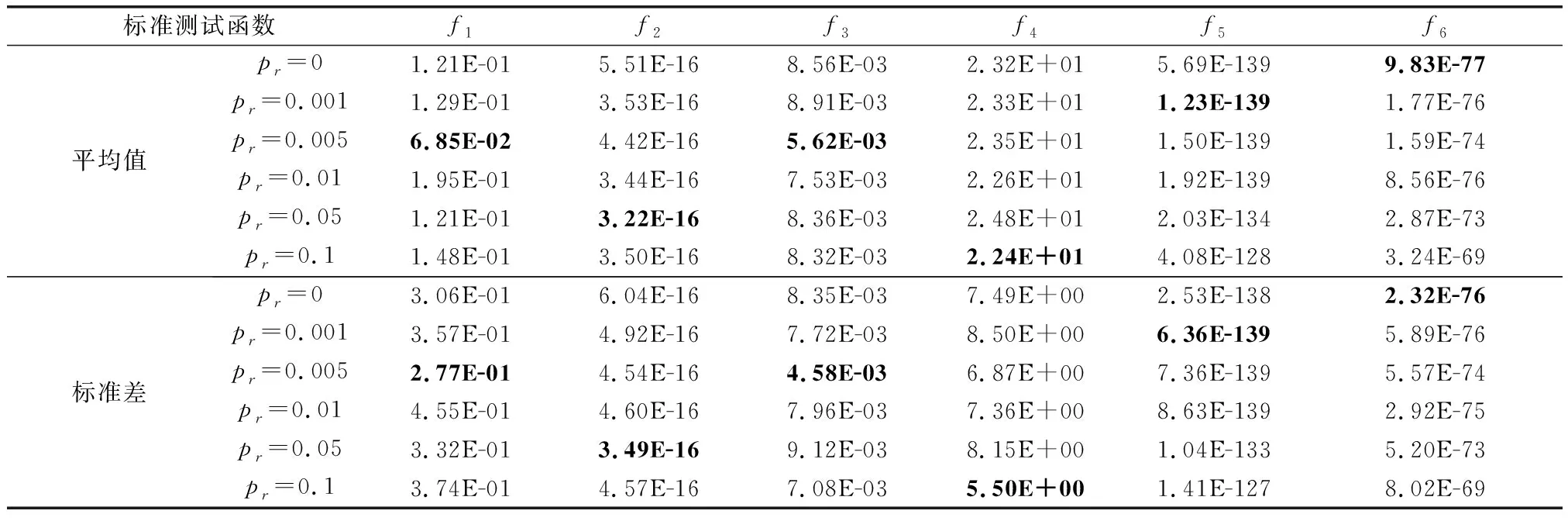
表3 GDBSO设置不同参数在30维度下寻优结果

仿真结果表明,在不同维度的单峰函数中,在[0,0.001]内取值,能让GDBSO有更高的寻优精度。这是由于单峰函数只有一个严格局部极大值,较小的值能充分发挥差分变异策略的作用,种群在最优值附近区域不断收缩,逼近最优值。

仿真结果表明,求解3维度、10维度多峰函数时,在[0,0.005]内取值,求解30维度多峰函数时,在[0.001,0.01]内取值,求解50维度多峰函数时,在[0.005,0.1]内取值,均能使GDBSO有更高的寻优精度。GDBSO求解多峰问题时,过大或过小都会降低算法寻优精度。过小值让算法加速收敛,但易陷入局部最优,过大值帮助算法跳出局部最优,但更像随机搜索,降低了搜索效率。找到合适的值,保证两者的平衡是提高GDBSO算法寻优精度的关键。高维度的多峰问题,复杂程度高,需要更大的概率跳出局部最优,则需要更大的值。而低维度的多峰问题,复杂程度相对低,更需要注重搜索效率,则需要较小的值。

3.2 不同算法比较

参考文献[2]设置BSO的特有参数:=20、=0、=1。文献[9]指出,MBSO设置在[0.001,0.1]范围内有更好的性能,再根据前文结论,MBSO、GDBSO均设置=0.005,保证算法都有较好的性能。仿真得到4种算法在4个维度下的仿真结果。3维度、50维度下仿真结果如表4和表5所示。

表4 不同算法在3维度下寻优结果

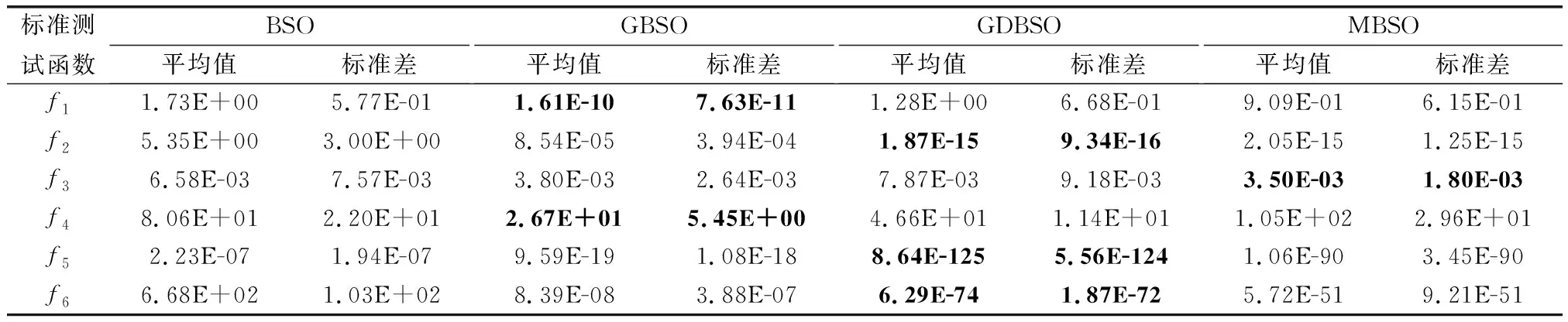
表5 不同算法在50维度下寻优结果

在不同维度的单峰函数中,GDBSO算法在寻优精度上均有极大的优势,平均值与标准差均优于其他3种头脑风暴算法。这是由于单峰函数只有一个严格局部极大值,采用追随全局最优策略与差分变异策略使得算法在该局部极大值附近收敛,极大提高寻优精度。

各算法求解不同维度多峰函数表现各异。在3维中,GDBSO寻优结果的平均值及标准差在4种算法中表现优异;在10维中,GDBSO与MBSO寻优精度相近,在Ackley、Apline、Griewank函数中表现较好,但在Rastrigin函数中表现略差于GBSO;在30维中,各改进型算法寻优精度相似,且均高于BSO。在50维中,GDBSO仅在Apline函数上表现最佳,在其他函数中表现一般。这是因为算法转入局部搜索后,个体更新受到全局最优的影响大,且变异系数小,使得搜索效率高,因此在更注重搜索效率的低维多峰问题中,GDBSO有更高的寻优精度,而随着维度上升,搜索效率重要性下降,精度优势逐渐削弱。

表6、表7给出了优化算法寻得可接受解的情况。平均迭代次数是指优化算法寻得可接受解时迭代次数的平均值,表征优化效率;成功率是指优化算法在仿真中寻得可接受解的概率,表征可靠性。表中横杆表示算法不能寻得可接受解。

从表6、表7可见,在3维和30维中,除了Griewank函数外,GDBSO寻得其他标准测试函数的可接受解时迭代次数最少,说明其优化效率最高。这是由于差分变异策略能实时捕捉搜索特征,加之变异前追随全局最优,能够更高效地得到更优解。

成功率对于优化算法来说是非常重要的,因为我们不知道将会面临什么样的问题,对于不同类型的问题,优先考虑具有较强可靠性的优化算法。从表6可见,GDBSO和MBSO均能在大部分低维度标准测试函数的极值寻优过程中,以100%的概率寻得可接受解。在中,各算法均无法保证100%寻得可接受解,GDBSO寻得可接受解的概率最高,为94%。因此,GDBSO求解低维问题时具有较强可靠性。

表6 3维度下的优化效率与可靠性

从表7可见,问题维度上升至30时,各优化算法可靠性下降,均无法寻得的可接受解。MBSO成功率均位居榜首,可靠性最强,GDBSO成功率紧随其后,可靠性仅稍差于MBSO。

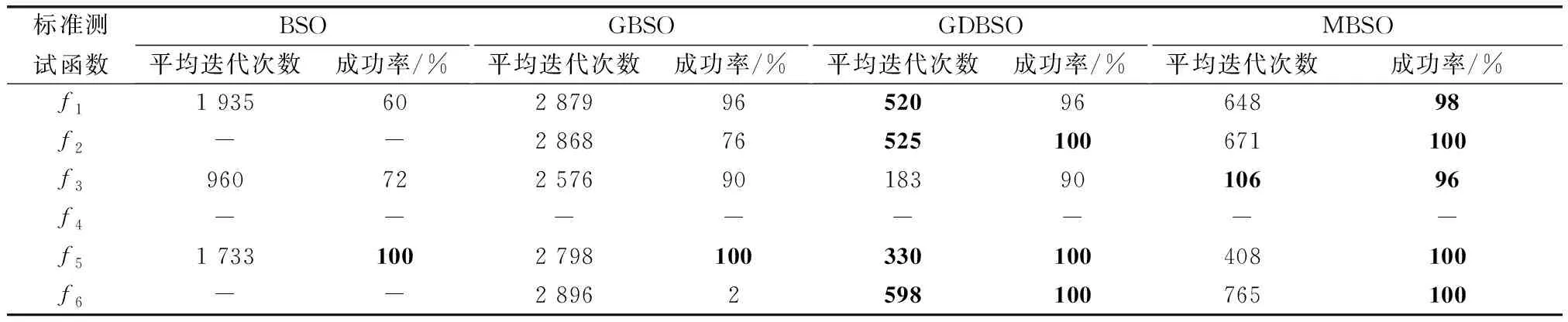
表7 30维度下的优化效率与可靠性

仿真结果表明,在求解各维度标准测试函数时,GDBSO收敛速度最快。10维Ackley、Apline和Sphere函数以及30维Griewank、Rastrigin、Schwefel函数的适应度变化曲线,如图2和图3所示。算法转入局部搜索后,变异步长小导致更新后的种群更加集中,而种群收缩使得步长变小,从而形成正反馈,加速算法收敛。加之算法在变异前还追随当前最优个体,收敛速度更快。

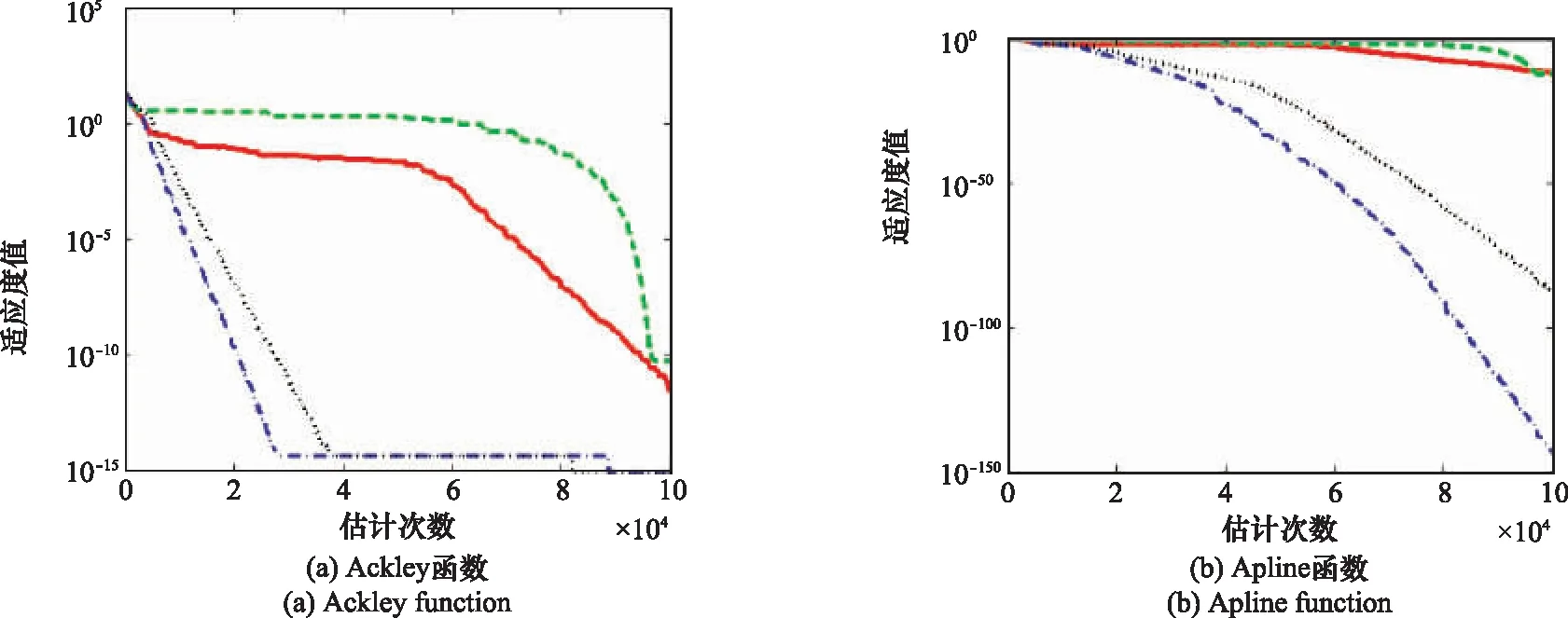
图2 10维部分函数适应度值变化曲线Fig.2 Variation curve of fitness value of several functions of 10 dimensions

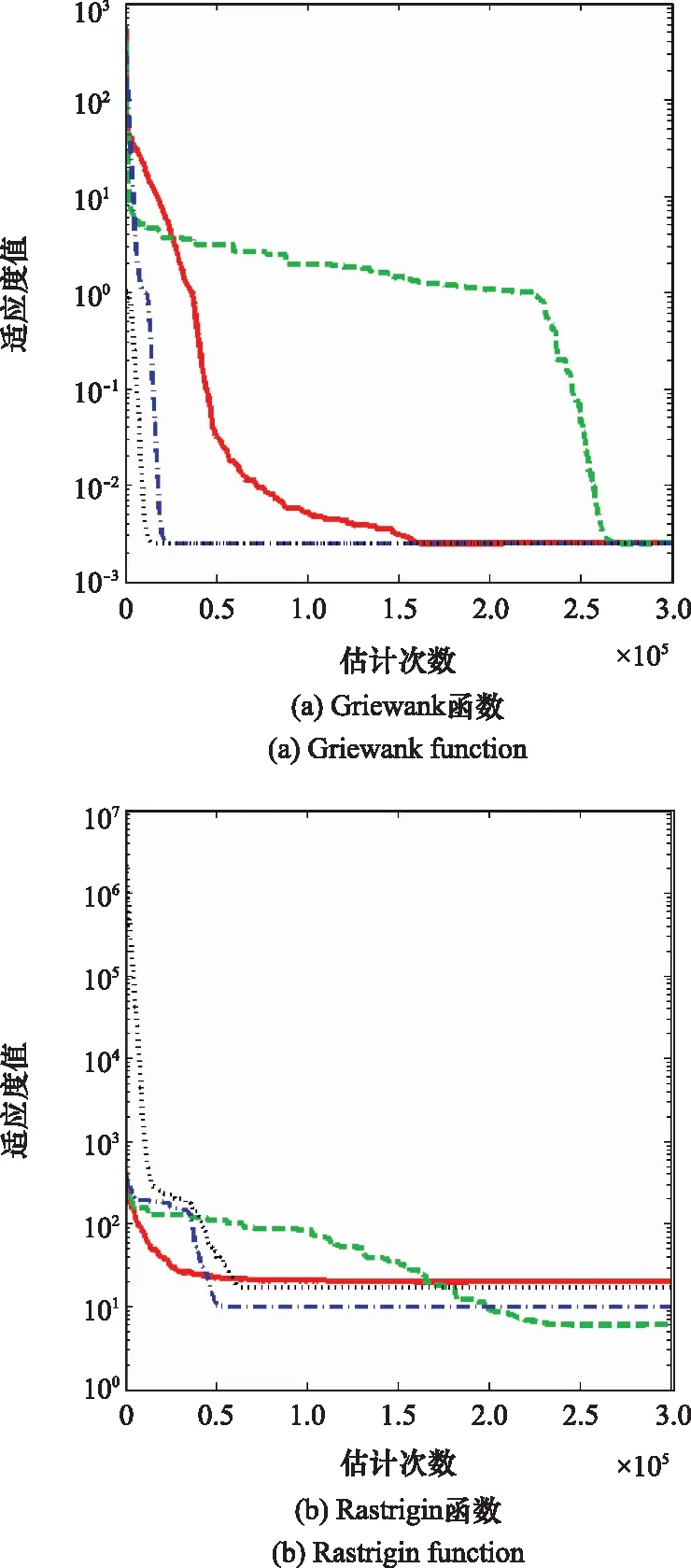
图3 30维部分函数适应度值变化曲线Fig.3 Variation curve of fitness value of several functions of 30 dimensions

4 应用实例

自主水下航行器(autonomous underwater vehicle,AUV)路径规划是保证其在水下安全隐蔽航行和可靠高效完成作战任务的关键技术。目前智能优化算法是路径规划算法的研究热点与未来重点。本文借鉴文献[26]提出的空间环境模型与路径规划策略,仿真验证GDBSO的有效性和可行性。

计算机仿真平台为Matlab 2014a,处理器为Intel(R)Core(TM)i7-7700 CPU @3.60 GHZ,RAM 8GB,操作系统为Windows7-64位。将振荡型IWO、GDBSO、GBSO、MBSO、BSO应用于AUV路径规划,各独立运行50次。水下空间参数设置参考文献[28],其中,障碍物水平面中心坐标为(133 100,25 400),禁航区水平面中心坐标为(133 200,25 400),AUV起点为(132 820,25 540,-80)、终点为(133 300,25 360,-80),水面舰艇布放位置为(132 950,25 440,-10),潜艇布放位置为(133 180,25 430,-130)。海流通过20个粘性Lamb涡流运动方程叠加而成,涡流中心位置随机给出,涡流强度为8,半径为2。

BSO及其改进型的参数设置参考第3节。振荡型IWO的参数设置参考文献[28]。算法的种群规模=30,问题维度=10。对算法终止条件的选取,本文进行了研究,先设置最大迭代次数为=200,路径代价变化曲线如图4所示。

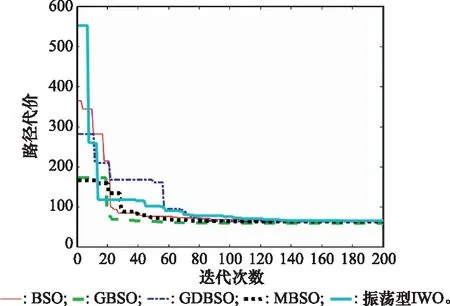
图4 最大迭代200次路径代价变化曲线Fig.4 Variation curve of path cost with 200 iterations

由图4可知,当迭代至100次时,各算法基本求得较优值。最大迭代次数增加使算法寻优结果更好,但花费的时间也随之大大增加。战场情况瞬息万变,AUV路径规划的实时性具有非常重要的意义。因此,设置最大迭代次数=100。

仿真得到的AUV规划路径如图5所示。图5中蓝色线条构成的类半球状图形表示武器平台的最大探测范围,红色线条构成的类半球状图形表示武器平台杀伤性武器的杀伤范围,黄色圆柱体表示禁航区的范围,青蓝色圆柱体表示障碍物的影响范围。蓝色短矢线表示矢线起点的海流方向与强度。

图5 不同算法规划的最优路径三维示意图Fig.5 Three dimensional diagram of optimal path planned by different algorithms

最优路径数据如表8所示。GDBSO算法规划的路径长度最长,但其航行时间最短。将最优路径局部放大得到图6,GDBSO与GBSO规划出的路径顺应海流方向,利用海流推动助力AUV运动。GDBSO充分利用海流,即使路径长度最长,也可以更快达到目的地。

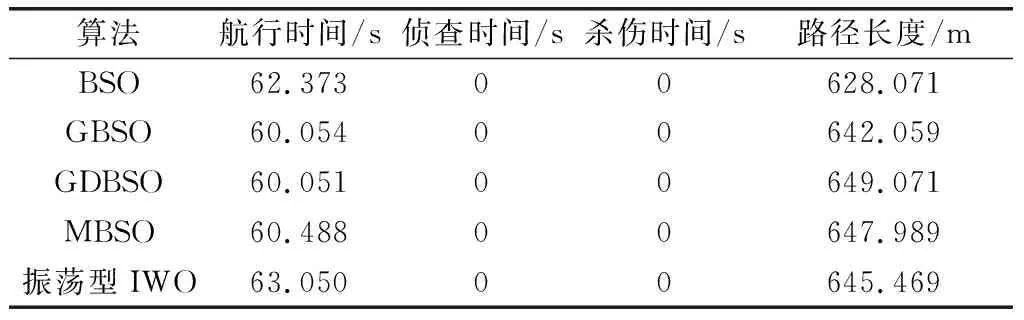
表8 不同算法规划的最优路径比较

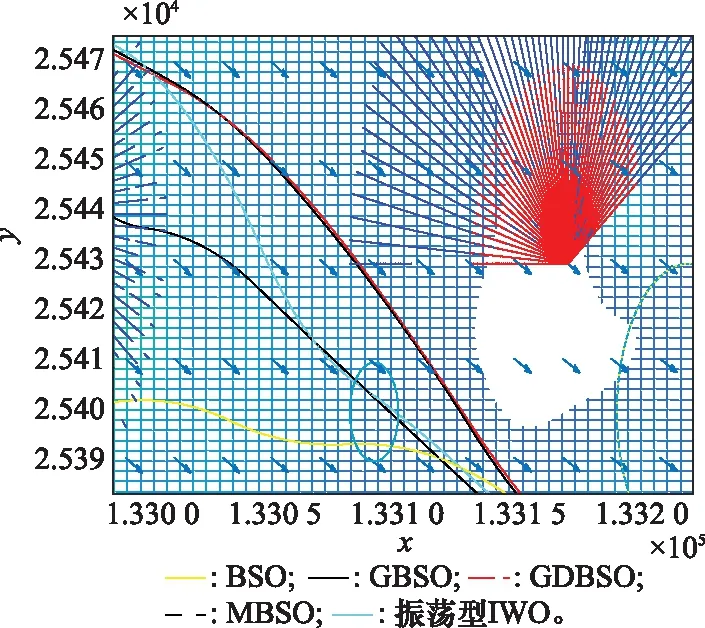
图6最优路径局部放大图Fig.6 Locally enlarged view of optimal path

算法运行50次的统计结果如表9所示。最优值表征算法找到更优解的潜力,表现最好的是GDBSO;最差值表征算法寻优的保底程度,表现最好的是振荡型IWO,GDBSO表现一般;平均值表征算法寻优结果的一般水平,表现最好的是GBSO,其次是GDBSO;标准差表征算法寻优结果的离散程度,表现最好的是振荡型IWO,GDBSO表现一般。这里的平均值是指去除最大最小值后的平均值,降低极端情况对最终计算结果的影响,更好地表征样本一般水平。

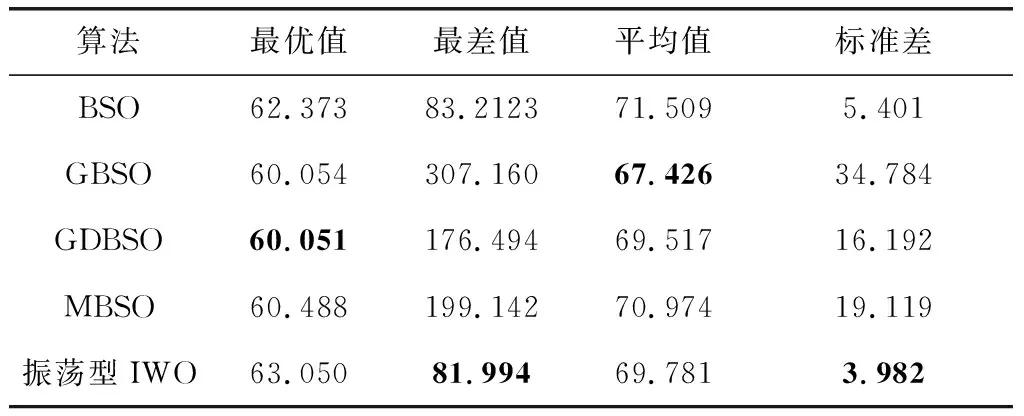
表9 不同算法的路径代价比较

从图4可见,5种算法规划路径时的收敛速度相近,因此在这里不作为算法性能评价标准。以最优值、最差值、平均值、标准差作为评价标准进行评分,得到表10。可见,GDBSO在AUV路径规划中有着最佳的综合表现。

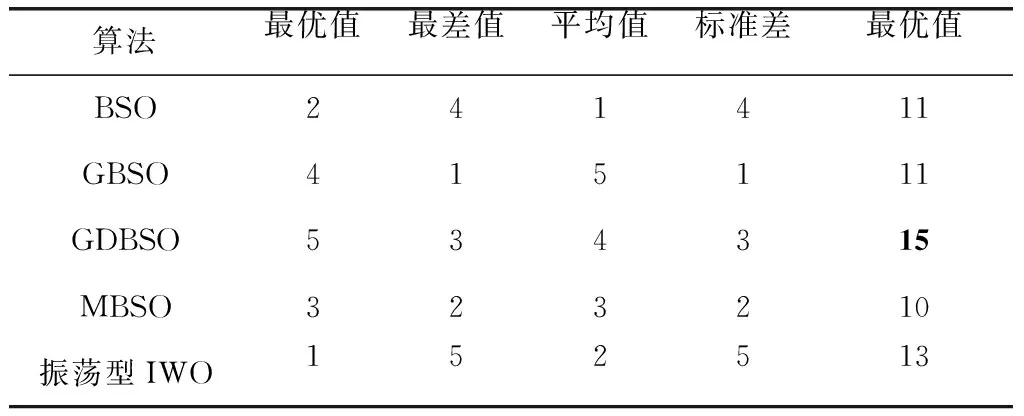
表10 不同算法规划路径评分表

5 结 论

本文分析了BSO算法,针对算法在选择操作中仅部分个体更新追随全局最优和变异操作中步长不能自适应的问题,应用了追随全局最优策略和差分变异策略,对BSO算法进行了改进。仿真结果表明改进算法在处理单峰函数时精度极高;处理低维多峰函数时也有较好寻优能力,但随着维数上升,寻优能力下降;求解大多数函数时都有很快的收敛速度、较高的优化效率和较强的可靠性。改进算法结合AUV路径规划应用的仿真验证表明算法找到更优解的潜力较高,能充分利用海流规划路径,并有着最佳的综合性能。改进算法的进一步理论分析和应用领域扩展仍是下一步的研究重点。