注意力机制CNN的毫米波大规模MIMO系统信道估计算法

刘紫燕, 马珊珊, 梁 静, 朱明成, 袁 磊

(贵州大学大数据与信息工程学院, 贵州 贵阳 550025)

0 引 言

毫米波大规模多输入多输出(multiple input multiple output,MIMO)作为5G关键技术,在提升移动通信系统性能方面因其具有的高速率和高效率得到了广泛运用。由于在收发端部署了大量天线,系统反馈、开销、信道矩阵尺寸变化给系统的通信质量带来了挑战。信道状态信息获取的准确性反应了系统的通信质量,对于毫米波大规模MIMO系统信道估计的研究具有重要意义。信号传播的过程中,受到外界环境、收发信机地理位置、系统配置等影响,对其产生大量数据信息进行学习有利于提取系统信息,为信道估计提供基础。深度学习作为人工智能领域的主要研究方法,其构建的网络模型对大量样本数据具有强大分析能力和识别能力。近年来,将深度学习用于解决通信系统信道估计、信号检测、预编码等问题具有较好鲁棒性为通信领域研究提供了新兴方向。

传统信道估计方法主要有最小二乘法(least square,LS)、最小均方误差(minimum mean square error,MMSE)和压缩感知算法。LS算法依据导频辅助作用进行线性插值估计未知信道响应信息,其导频开销大,对多天线系统估计精度较差;MMSE算法需要基于信道的统计特性和先验信息,计算复杂度高;压缩感知算法通过重构恢复对信号进行处理,对信道的特性具有稀疏性要求。近几年将深度学习方法用于解决信道估计问题受到学者们的关注。将信道矩阵视作二维图像,其方式区别于传统信道估计算法,通过图像处理方法进行信道估计。文献[17]基于导频辅助作用,通过已知位置的信息估计出信道响应的未知值。但其方法依然依赖于导频的辅助作用,训练过程中导致系统开销大。随着天线数目的增大,在图像转换过程中存在矩阵维数大的问题,还需要对图像进行去噪、边缘优化等操作。文献[18]引入去噪卷积神经网络(denoising convolutional neural network,DnCNN)对信道矩阵图像进行去噪处理,该网络的性能优于基于压缩感知的算法。而DnCNN是针对特定的噪音水平量身定做的,只有当噪音水平在训练范围内时效果才显著。因此,将信道矩阵视为自然图像进行训练,采用深度学习训练模型估计方法,可适用于多种信号噪声级别及空间相关噪声，并可以提升训练速度。在去噪过程中,由于前期需要人为设定噪声水平,而噪声通常是与通道和空间相关的,卷积神经网络(convolutional neural network, CNN)在去噪方面具有较好的鲁棒性。

基于导频的信道估计方法，会产生导频污染与开销从而影响通信性能,基于深度学习的信道估计方法可以不依赖导频信号的辅助,根据信道特性采取图像去噪的方式解决信道估计问题。由于系统受噪声影响,为提升去噪泛化能力和估计精度。本文提出一种基于注意力机制的CNN的信道估计方案,以CNN为基础网络,融合注意力机制构建信道估计网络模型。将信道矩阵视为图像进行去噪处理,通过CNN提取信道噪声信息,结合注意力机制增强图像噪声特性并进行特征融合提取噪声,该网络具有良好的去噪效果。

1 系统模型

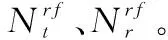
在时刻,系统传输的数据流为,经系统传输,第个用户向第个基站端发送信号,接受信号可以表示为

=,+

(1)

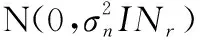
在生成信道路径后,信道矩阵可由信道响应加权相加,信道矩阵可以表示为

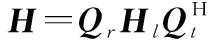
(2)

式中:=diag(,,…,);和分别是收发端阵列响应矩阵。

考虑到大规模天线系统中天线间的相关性和毫米波在传播过程中经历散射次数有限,信道,元素之间存在一定相关性,信道呈现稀疏特性。依据此特性,可将信道矩阵看作二维自然图像,考虑信道噪声的影响,采用图像去噪技术提取信道噪声部分,通过网络模型进行训练和测试,得到估计的信道矩阵,从而实现信道估计。

2 基于注意力机制的CNN信道估计

2.1 基于注意力机制的图像特征提取

注意力机制被广泛运用在自然语言处理、图像识别、语音识别等领域,是深度学习技术中关键核心技术之一。其与人类视觉注意力机制相似,通过注意力机制可以从大量信息中快速提取出有效的信息,极大提高信息处理的效率。

注意力机制的过程如图1所示,其过程主要分为3个阶段:第一阶段为将从模型的卷积层中提取得到, (0≤≤,0≤≤),其中、表示图片的大小,通过传输到注意力层,将得到, 计算与各个元素,=之间的相关性。表达式为

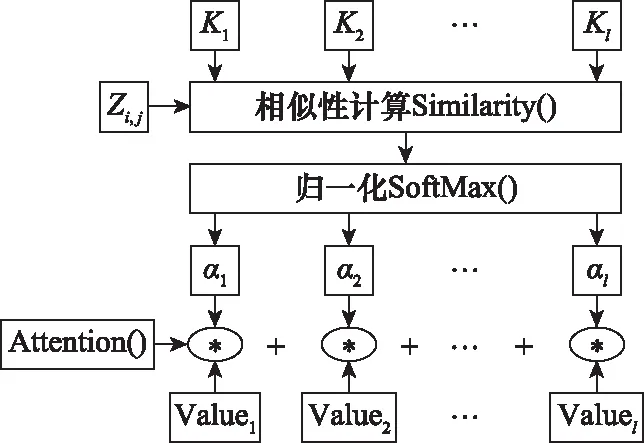
图1 注意力机制计算过程Fig.1 Computation process of attention mechanism

Similarity (,, )=,

(3)

第二阶段对第一阶段的结果进行数值转换,进行归一化处理,引入SoftMax。表达式为

, =SoftMax(Sim, )

(4)

第三阶段将, 与中对应的权重值Value, 进行加权求和得到权重值。表达式为

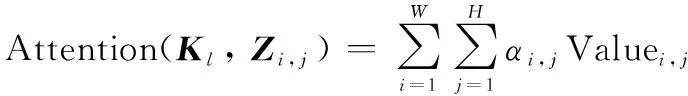
(5)

其输入是从卷积层中提取到的特征,输出是该特征的注意力权重。

算法 1 注意力机制算法输入:卷积层提取特征Zi,j输出:权重Attention1. W,H2. Similarity (Kl, Zi,j)=KlZi,j3. αi,j=SoftMax(Simi,j) 4. for i < 0 to W do;5. for j < 0 to H do;6. Attention (Kl, Zi,j)=∑Wi=1∑Hj=1αi,j·Valuei,j7. end for8. end for

2.2 基于注意力机制CNN信道估计

CNN是由基础的神经元之间线性加权组成,并且是具有卷积结构的深度神经网络。卷积结构可以有效减少网络参数,缓解模型过拟合问题。其特征提取功能的核心模块是由网络中隐含层的卷积层和池化层组成,是一种多层的监督学习神经网络。该网络模型中的权重参数逐层调节主要通过梯度下降法最小化损失函数,通过不断的迭代训练可以提高网络的性能。因此,在图像分类、识别、去噪等领域得到广泛运用。

CNN包括卷积层、激励层、池化层和全连接层,其网络结构如图2所示。卷积层(Conv)可以实现对输入图片的特征进行提取,其具有局部感受野和权值共享两个特性。池化层(BN)可以降低网络参数并避免特征维数大而出现过拟合问题。激励层(Relu)为了防止数据中存在较大或小的数据对训练效果弱化。全连接层通过进行特征融合并输出。

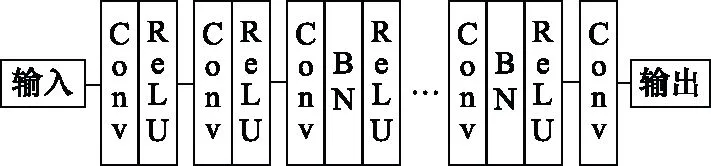
图2 CNN结构Fig.2 CNN structure

本文提出基于注意力机制CNN的信道估计模型如图3所示,其中模型由基础的CNN和注意力机制网络组成,将信道矩阵看作二维图像输入到网络模型中。

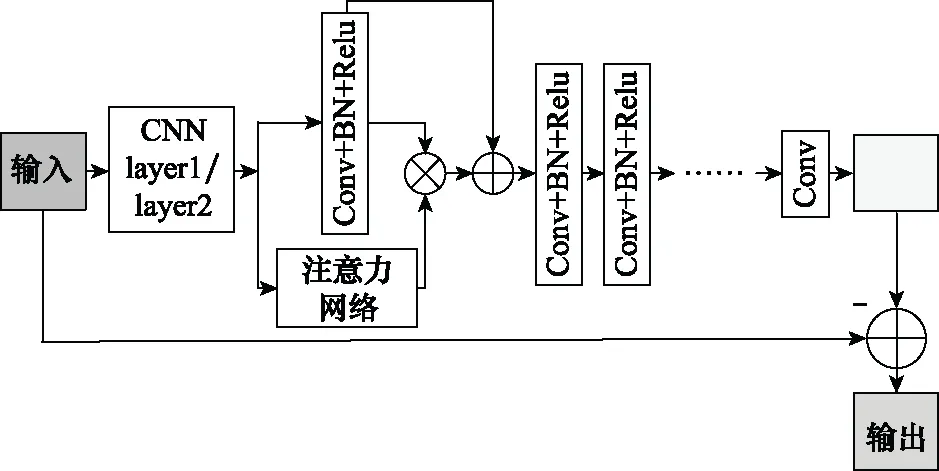
图3 基于注意力机制CNN的信道估计模型Fig.3 Channel estimation model based on attention mechanism CNN

通过CNN前两层提取图像的浅层特征,将CNN提取的浅层特征输入到注意力网络中,通过结合注意力机制网络提取的特征,融合后得到显著特征。最后,将提取的特征通过卷积层进行噪声提取,将提取的噪声通过全连接层输出。输入是含信道噪声矩阵,通过模型提取噪声,输出是估计信道矩阵。整个模型包含15层,除layer1层、layer2层和输出全连接层外,每层由Conv+BN+Relu组成,其中Conv代表卷积,BN代表批量归一化,Relu代表激活函数采用Relu函数,卷积核采用3×3×64大小。

2.3 评价指标

本文主要采用归一化均方误差(normalized mean square error,NMSE)来评价信道估计质量。其是用来衡量估计量与被估计量之间差异程度,表达式为

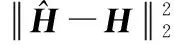
(6)

2.4 复杂度分析

表1为本文提出和对比算法的复杂度比较,其中为子载波数,为路径数。基于深度学习的信道估计方法,主要考虑以在线估计的复杂性为度量。

表1 算法复杂度对比

由表1可知,考虑在线估计阶段,本文所提算法的复杂度高于LS,但较LS估计精度有较大提升,复杂度低于MMSE。主要是神经网络进行在线训练,将已经训练好的网络用于估计,通过对矩阵进行乘法加权无需进行求逆,其复杂度较低。所提算法低于CNN,与DnCNN复杂度处于同等级,因增加了注意力机制,相较于CNN和DnCNN收敛得更快,相较于DnCNN可以得到更高的估计精度。

3 仿真结果与分析

本文所采用的数据集主要模拟在十字街道上分布的建筑物、基站和用户之间的通信场景,通过DeepMIMO捕捉周围环境和位置信息,将产生的数据通过网络模型进行训练并估计信道状态信息。首先通过文献[30]的方式产生数据集,将得到的信道矩阵输入到网络中。数据集的产生中提供了18个可以选择的基站,本文选定了第5～8个基站。在其分布的100万多用户中选取第1 200～1 800行的用户。基站天线数=××,分别代表基站,,方向上天线的数量,参数设置如表2所示。其次选取样本数40 000,其中75%用于训练数据集,15%用于验证数据,10%用于测试数据。最后本文将所提出的算法与LS、MMSE、CNN、DnCNN方法进行比较分析。

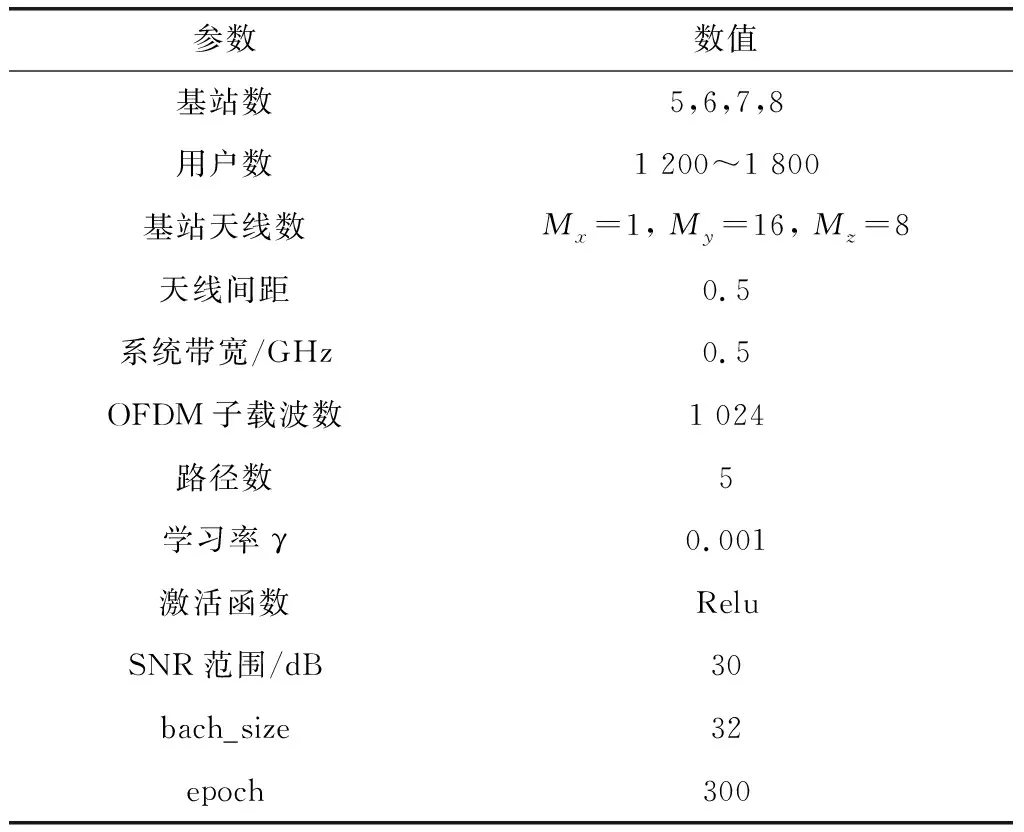
表2 系统仿真的主要参数

图4分别对比了CNN、DnCNN 2种方法和所提方法在不同迭代次数下各网络模型的损失。通过设定相同网络参数,在不同迭代次数下,优于基于注意力机制模块的优化,在提取特征时更加注重需要关注的特征而忽略不重要的特征,基于所提方法的网络模型在损失性能上优于CNN、DnCNN。

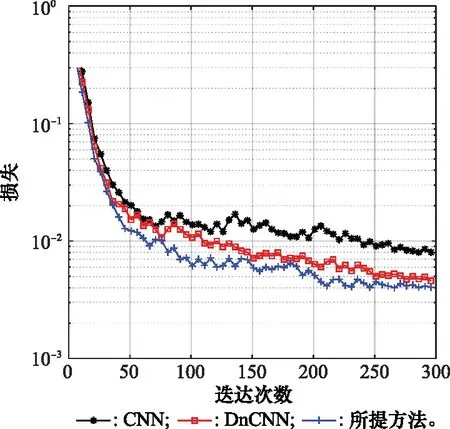
图4 不同迭代次数下各网络模型的损失Fig.4 Loss of each network model under different iteration times

图5～图7分别对比了在信噪比(signal to noise ratio, SNR)分别为10 dB、20 dB、30 dB时,CNN、DnCNN两种方法和所提方法在不同网络层数下各网络模型的NMSE性能比较。从图4～图6可以看出,通过不断增加网络层的数量来对比模型的估计性能,所提方法在相同网络层数下性能优于CNN、DnCNN方法。从图4可以看出,当网络层数为9和11时,可以发现所提方法和DnCNN方法的NMSE性能在同一等级。从图5可以看出,当网络层数为9和10时,可以发现所提方法和DnCNN方法MSE性能在同一等级。此外,所提方法在12层内收敛,而CNN、DnCNN在15层和14层收敛。从图6可以看出,当网络层数为9和13时,可以发现所提方法和DnCNN方法MSE性能在同一等级。此外,所提方法在11层内收敛,而CNN、DnCNN在14层和13层收敛。本文方法模型上较其他简单和实用。随着神经网络层数的增加,所提方法都能取得更好的NMSE性能。

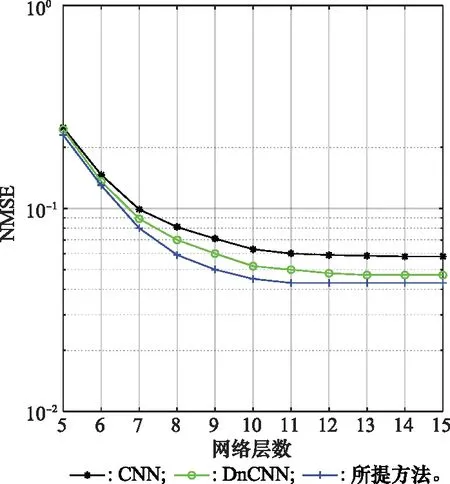
图5 不同网络层数下各网络模型的NMSE性能比较(SNR=10 dB)Fig.5 NMSE performance comparison of various network models under different network layers (SNR=10 dB)

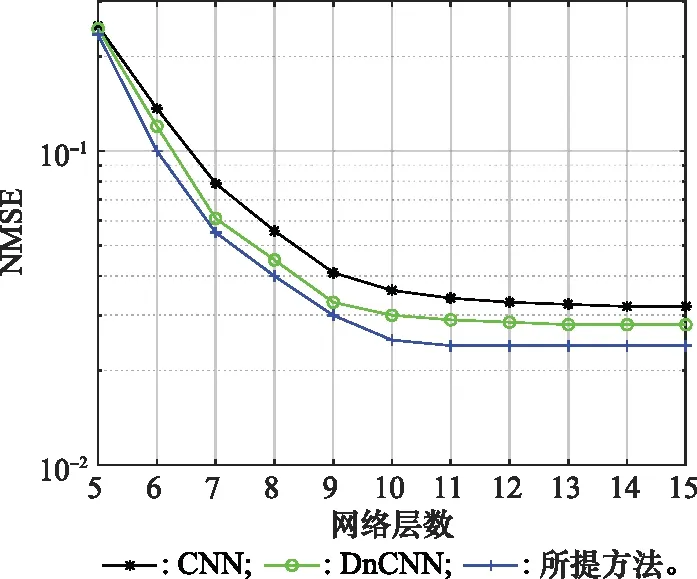
图6 不同网络层数下各网络模型的NMSE性能比较(SNR=20 dB)Fig.6 NMSE performance comparison of various network models under different network layers (SNR=20 dB)

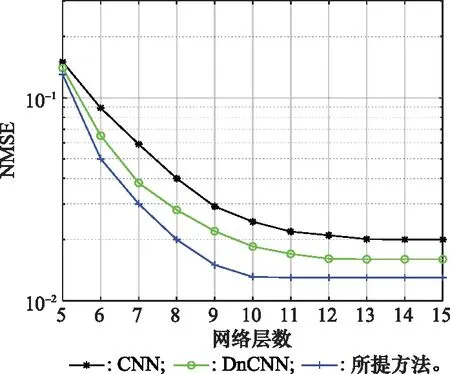
图7 不同网络层数下各网络模型的NMSE性能比较(SNR=30 dB)Fig.7 NMSE performance comparison of various network models under different network layers (SNR=30 dB)

图8分别对比了LS、MMSE、CNN、DnCNN 4种方法和本文所提方法在不同SNR下的NMSE性能,其中LS和MMSE为传统信道估计算法。LS算法的估计性能最差,MMSE算法较LS算法有一定的提升。从图8可以看出,本文所提方法较CNN、DnCNN方法估计性能平均提升约1.53 dB。在SNR为0～15 dB情况下,比CNN、DnCNN方法估计性能平均提高约0.15～0.23 dB;在16～30 dB情况下基于所提方法的信道估计性能平均提高约0.68～1.43 dB。由于所提方法对样本进行训练学习时增加了注意力机制模块,在噪声提取上表现出了更好的性能,在同一SNR下,基于所提方法的信道估计精度平均提升约1.86 dB。

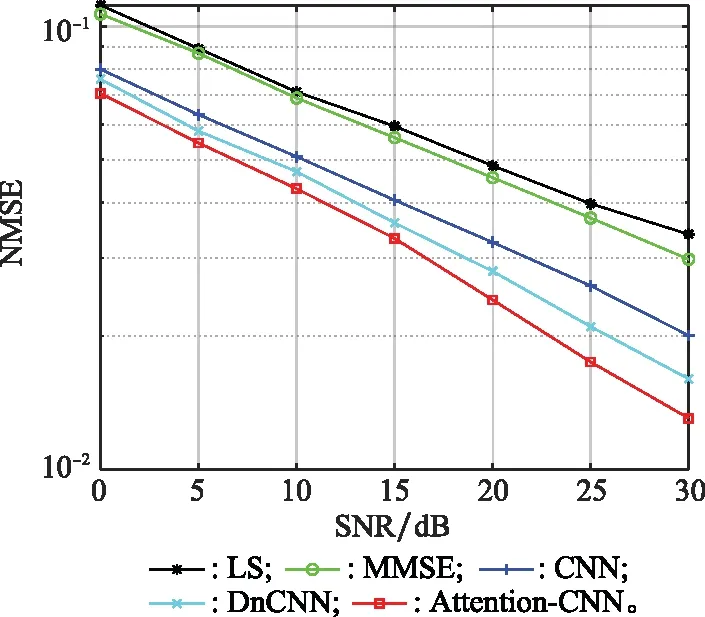
图8 基于Attention-CNN和其他方法的NMSE曲线Fig.8 Normalized mean square error curves based on Attention-CNN and other methods

深度学习方法应用于通信领域主要得益于对未知模型强大的学习能力,提出基于注意力机制CNN方法相较于其他方法性能有所提升。本文通过选取分布的基站中较为集中的几个基站和多个用户产生更符合实际通信场景的数据,仿真结果表明,在不同SNR情况下,其估计精度有所提升,并且随着信噪比增加,NMSE减小,估计性能越好。

4 结 论

针对信道估计受噪声、系统性能影响的问题,本文通过DeepMIMO模拟产生数据集,将产生信道矩阵视为图像的方式。本文通过注意力机制模块增强图像空间像素特征,将注意力机制结合CNN对图像进行去噪。结果表明,本文所提算法的信道估计精度较其他方法有所提升。下一步的研究方向是创建更切合真实环境的数据集,其他图像的处理方式提取信道特征以及更简单的网络模型提升信道估计的精度。