单边Lipschitz非线性多智能体系统一致性追踪控制

罗 哲, 权婉珍,*, 张朴睿, 杨小冈

(1. 火箭军工程大学导弹工程学院, 陕西 西安 710025; 2. 国防科技大学航天科学与工程学院, 湖南 长沙 410073)

0 引 言

近年来,多智能体系统协同控制已经成为许多学者关注的热点,被应用到多无人机编队控制、传感器网络同步、多机器人协作、多导弹协同攻击、分布式电网控制、多卫星组网技术等领域。一致性控制是各个智能体根据邻居状态信息设计的一种协作策略,在环境变化的影响下各个智能体仍然能利用这种策略使共同关注的状态信息达到一致。

目前,多智能体系统的一致性问题已经被广泛研究。文献[15]基于一致性理论,提出了一种二阶线性多智能体系统时变性能编队控制协议,适用于实际中无人机电池和燃料等资源有限的情况,验证了所设计的控制协议不仅能够形成期望的编队,同时系统所消耗的能量小于给定的系统总能量。文献[16-17]考虑到多智能体系统中部分状态不可测,提出了多智能体系统的输出一致性控制。文献[18-19]研究连续时间和离散时间的混合多智能体系统一致性问题,利用博弈论的方法对两组智能体建模,获得了系统一致的充分必要条件。文献[20]设计了一种改进的控制协议,可抑制外界扰动并实现了多智能体系统的一致性。上述研究都是针对线性系统,线性系统比较简单,易于分析,但由于实际中几乎所有系统是非线性的,很难用线性去刻画出实际物理系统的非线性本质。

为了解决以上线性系统所带来的缺陷,Lipschitz非线性系统的一致性问题引起了学者的广泛关注和深入研究。文献[21-22]研究了基于状态观测器的Lipschitz非线性系统,巧妙地利用分离原理,获得了系统稳定的充要条件。文献[23]针对二阶Lipschitz非线性无领导者有限时间一致性问题,提出了有限时间一致性算法,使多智能体在有限的时间内达到平衡状态。文献[24-25]以Lipschitz非线性多智能体系统为研究对象,考虑了智能体之间通信链路中断问题,提出了切换拓扑条件下的一致性追踪控制器,获得了Lipschitz非线性系统一致性跟踪的充分条件。文献[26]针对任意有向网络结构,设计了带有动态增益的一致协议,实现了在马尔可夫切换拓扑下高阶非线性多智能体系统的一致性控制。以上文献主要是Lipschitz非线性系统为研究对象,分别从Lipschitz非线性多智能体之间的通信拓扑结构、收敛时间、状态不可测等方面进行一致性分析和设计,并取得了一定的研究结果,较之前线性系统具有更强的工程应用价值(如单连杆柔性机械臂系统、航天器姿态控制系统、蔡氏电路系统)。但通常情况下,Lipschitz非线性多智能体系统的Lipschitz常数必须为正数,从而限制了非线性函数的增长速率,这使得Lipschitz条件常数具有局限性,将会给系统带来保守性。

针对上述Lipschitz条件常数所带来的局限性问题,本文研究了单边Lipschitz非线性多智能体系统一致追踪控制。相比较以上的线性和Lipschitz非线性系统,本文研究的单边Lipschitz非线性多智能体系统主要有以下特点:首先,单边Lipschitz非线性多智能体系统的单边Lipschitz常数可以为负数、零和正数,克服了Lipschitz常数的局限性,降低了系统的保守性。其次,解决了Lipschitz常数因系数增大而失效的问题。因此,本文所提出的单边Lipschitz非线性系统具有更强的实际工程应用意义,有待进一步的深入研究。

1 预备知识及问题描述

1.1 预备知识:图论

=((),())表示多智能体构成的一个有向通信拓扑结构图,其中非空集()={,,…,}表示图的节点集,节点表示智能体,()⊆()×()表示边集,每条边由一对节点(,)来表示,表示智能体与智能体之间的通信关系,其中代表父节点,代表子节点。={:(,)∈()}表示节点的邻居节点的集合。图的拉普拉斯矩阵定义为=()-(),其中非空集()=[]∈×表示邻接矩阵,表示边的权重,≥0且>0当且仅当(,)∈(),()=diag{,,…,}表示入度矩阵。

1.2 问题描述

假设+1个非线性智能体具有相同的结构,并构成了一个单边Lipschitz非线性领导-跟随者多智能体系统,其动力学模型如下:

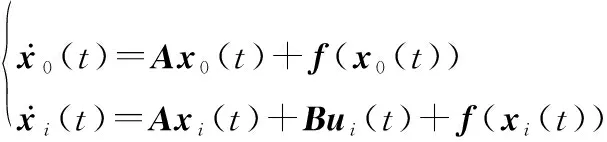
(1)

式中:()和()分别代表领导者和跟随者的状态;()代表其对应的控制输入。单边Lipschitz非线性函数()∶×[0,+∞)→是连续可微的,且满足单边Lipschitz条件和二次内部有界条件如下:

(2)

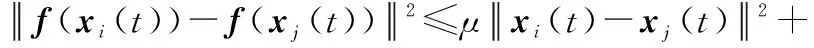
(3)

式中:表示单边Lipschitz常数;和是已知的常数。

本文研究的单边Lipschitz条件优势在于其常数,和可以为正数、0、负数,而Lipschitz条件常数>0。即单边Lipschitz条件和二次内部有界条件代表了更广泛的一类非线性函数,而传统Lipschitz条件不具备所有非线性动力学特性。在这种情况下,研究的单边Lipschitz非线性多智能体系统具有更广泛的应用价值。此外,基于Lipschitz条件的非线性控制方法对Lipschitz常数具有很强的依赖性,通常要求其较小,当Lipschitz常数很大时,很难找到一个可行的解。因此,基于单边Lipschitz条件和二次内有界的单边Lipschitz非线性多智能体系统的研究具有十分重要的意义。

为了解决单边Lipschitz非线性多智能体追踪问题,考虑控制协议:

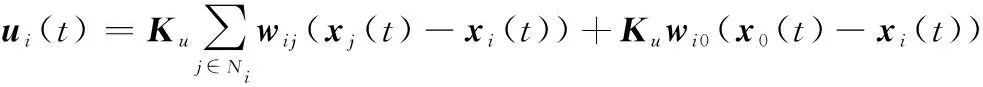
(4)

式中:=1,2,…,;是有待设计的控制增益矩阵。单边Lipschitz非线性多智能体系统一致性追踪控制的定义为:如果存在一个控制增益矩阵使得lim→∞(()-())=0(=1,2,…,)成立,那么通过设计控制增益矩阵,单边Lipschitz非线性领导-跟随者多智能体系统式(1)在控制协议式(4)的作用下可实现一致性追踪。

本文主要研究如何设计出合适的增益矩阵使单边Lipschitz非线性领导-跟随者多智能体系统实现一致性追踪控制。

2 控制协议设计

本节给出单边Lipschitz非线性领导-跟随者多智能体系统一致性追踪控制设计的充分条件。

首先,根据控制协议式(4),可得

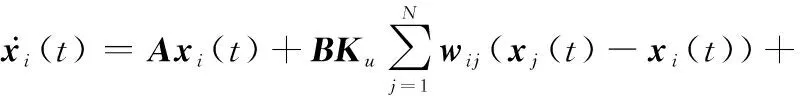
0(()-())+(())

(5)

令状态差()=()-(),在控制协议式(4)和式(5)的作用下,单边Lipschitz非线性领导-跟随者多智能体系统可转化为误差系统:

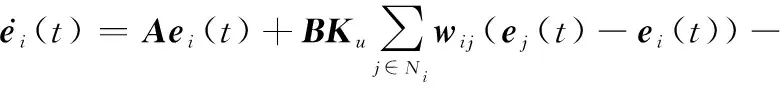
0(())+(())-(())

(6)

对于领导-跟随者结构作用拓扑为

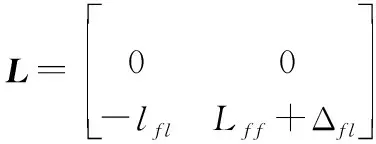
=[,,…,1]

=diag{,,…,1}

式中:表示领导者与跟随者的通信拓扑;表示跟随者之间的通信拓扑。通信拓扑包含生成树且跟随者之间的拓扑是无向的,则矩阵+是对称的。因此,存在一个正交矩阵满足条件(+)=diag{,,…,},且拉普拉斯矩阵的特征值>0(=1,2,…,)。

对于任意给定的系统参数>0,>0,存在矩阵=使得

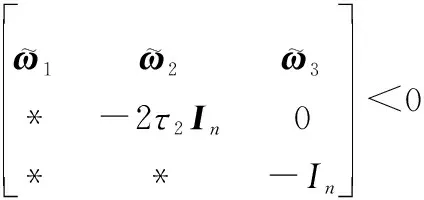
成立。其中,*表示对称矩阵。那么通过将控制增益矩阵设计为=,可保证单边Lipschitz非线性领导-跟随者多智能体系统式(1)在控制协议式(4)的作用下实现了一致性追踪控制,其中:

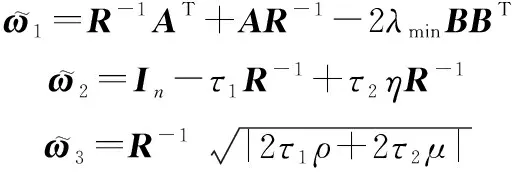
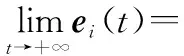
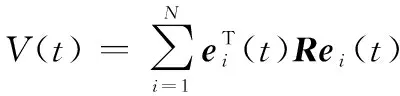
(7)

式中:=1,2,…,;=>0,可以看出()>0。将()沿着误差系统式(6)的解对时间求导可得

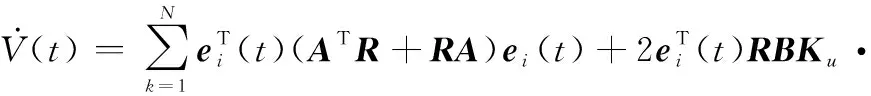
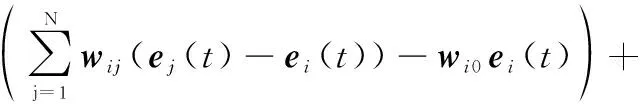
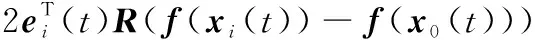
(8)

根据单边Lipschitz非线性条件式(3),下面的不等式成立:

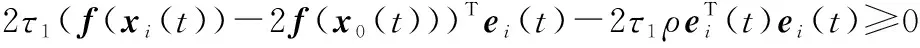
(9)

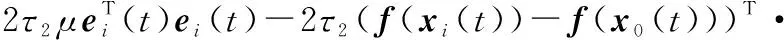
(10)

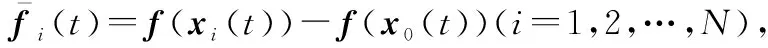
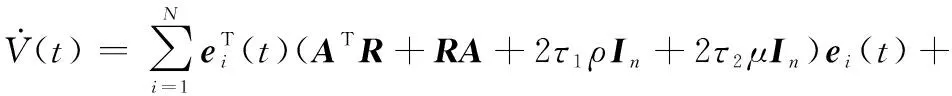
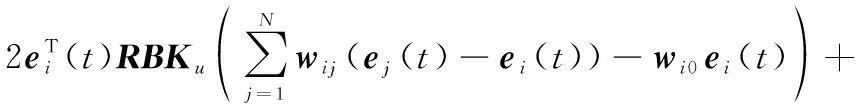
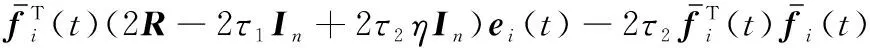
(11)

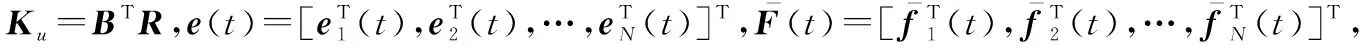
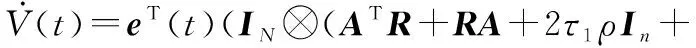
(12)

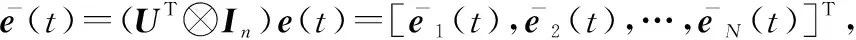
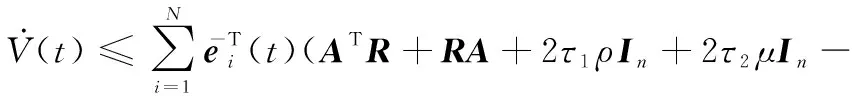
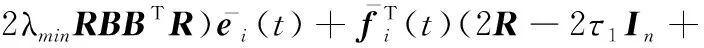
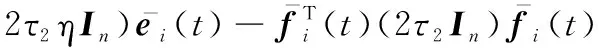
(13)

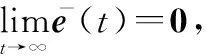
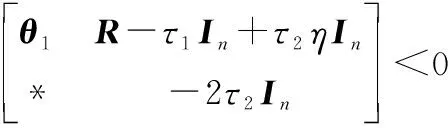
(14)

式中:

=++2+2μ-2

对式(14)左乘右乘diag{,},等价变化可得

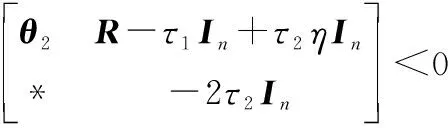
(15)

式中:

=++(2+2μ)-2

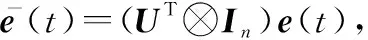
证毕

定理给出了单边Lipschitz非线性系统中控制协议式(4)的设计判据。下面考虑在控制增益矩阵给定的情况下,给出了单边多智能体系统实现一致性的分析判据。

对于任意给定的控制增益矩阵,存在一个对称正定矩阵=>0使得

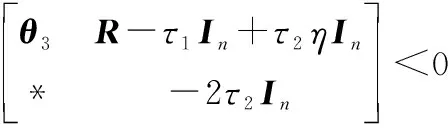
成立,那么单边Lipschitz非线性领导-跟随者多智能体系统式(1)在控制协议式(4)的作用下实现了一致性追踪控制。其中，=++2+2μ-2。

3 仿真分析

本节通过一个数值仿真实例对单边Lipschitz非线性系统的一致性追踪控制算法的有效性进行仿真验证。

单边Lipschitz非线性领导-跟随者多智能体系统由1个领导者和6个跟随者构成,其中每个智能体的动力学方程由式(1)表示,系统矩阵为

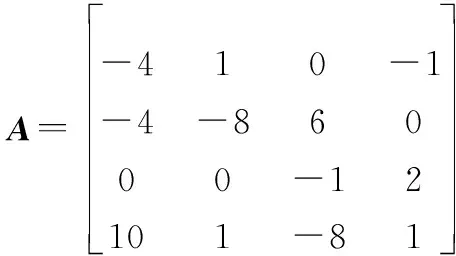
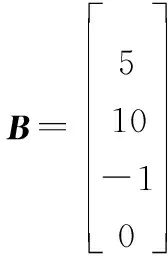
单边Lipschitz非线性函数(())(=0,1,…,)为

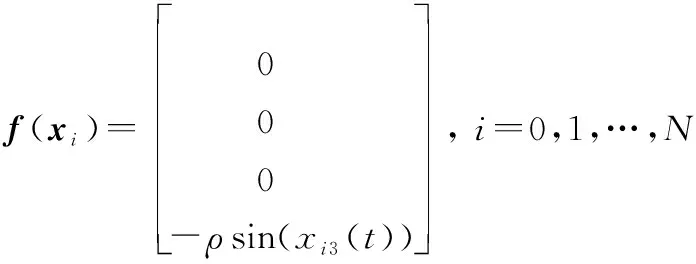
式中:函数()满足条件单边Lipschitz条件式(2)和二次内部有界条件式(3)。图1表示领导跟随者的通信拓扑结构图,其中拓扑图的权重都是0-1的。

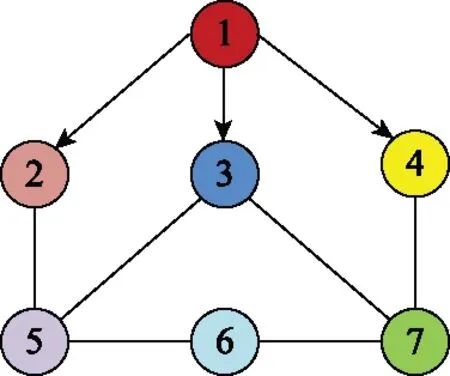
图1 通信拓扑结构图Fig.1 Communication topology

每个智能体的初始状态如下:

(0)=[02,03,15,06]
(0)=[12,08,-13,04]
(0)=[-15,05,12,09]
(0)=[-11,09,-06,03]
(0)=[-15,12,-12,10]
(0)=[-12,13,10,-08]
(0)=[13,02,11,-12]

选择参数=01,=-5,=015,=02和=5。根据LMI工具箱的FEASP求解器求出:

则控制增益:

==[3612 2,0949 1,0390 6,3756 0]

图2～图5表示了状态量的运动轨迹,其中红色圆圈表示领导者的运动轨迹曲线,其他不同颜色的曲线表示不同跟随者的状态运动轨迹。图2～图5分别表示状态量1(),2(),3()和4()(=0,1,…,6)的运动轨迹。从图2～图5的仿真结果可以看出,最后跟随者的状态与领导者的状态达到一致,因此可以得出在控制协议式(4)的作用下,单边Lipschitz非线性领导-跟随多智能体系统式(1)实现了一致性追踪。

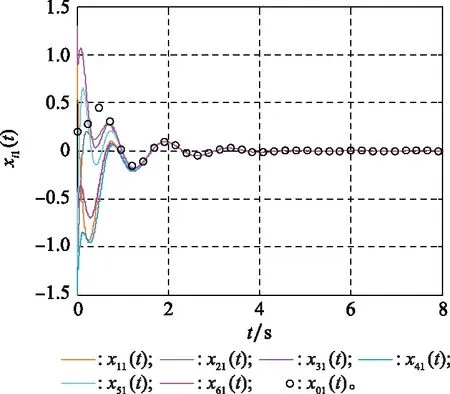
图2 状态xi1(t)的轨迹曲线Fig.2 Trajectories of the state xi1(t)

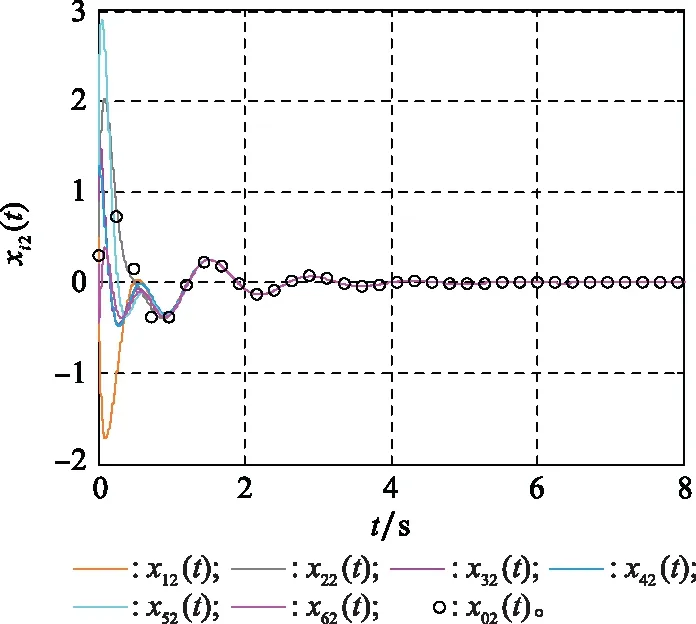
图3 状态xi2(t)的轨迹曲线Fig.3 Trajectories of the state xi2(t)

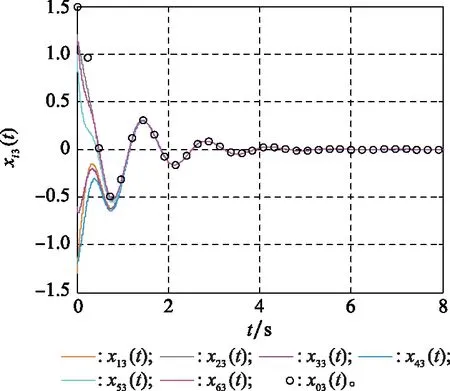
图4 状态xi3(t)的轨迹曲线Fig.4 Trajectories of the state xi3(t)

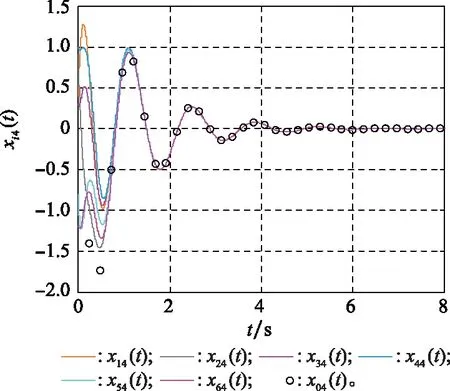
图5 状态xi4(t)的轨迹曲线Fig.5 Trajectories of the state xi4(t)

4 结 论

本文研究了单边Lipschitz非线性多智能体系统的追踪控制问题。首先,提出了分布式一致性控制协议。然后,利用正交变换,将一致性协议的设计问题转化为系统稳定性问题。同时,给出了单边Lipschitz非线性多智能体系统追踪控制的充分条件。理论结果表明,所设计的控制协议能够实现领导者和跟随者之间状态一致,即实现了一致追踪控制。最后,通过仿真算例验证了本文所提出方法的正确性。在未来工作中,将考虑一般非线性系统的一致追踪问题。