舰载导弹系统故障率及保修期模型优化

张怀强, 李铁成, 杜军岗

(海军工程大学管理工程与装备经济系, 湖北 武汉 430033)

0 引 言

舰载导弹系统由舰船上的导弹、攻击雷达、火控计算机等设备组成,用来完成攻击和防御任务。舰载导弹系统的使用目的是毁伤目标或使之无效,能否完成其预期使命任务是设计方、制造方和驻舰官兵最为关心的问题,因此各方对舰载导弹系统可靠性的关注度越来越高。美国海军因长期奉行有偿保修的装备售后策略,近年来舰船装备故障频发,海军舰船装备保修政策亟待调整。2016年,美国政府问责办公室(government accountability office,GAO)首次建议美国海军在舰船采购合同中调整舰船售后保修协议。2019年,GAO再次勒令美国海军重视导弹护卫舰的保修权益,尤其是要调整舰载导弹的保修策略。随着近年来海军新型舰船“下饺子”般批量入役,舰载导弹系统的升级换代也持续加快,极大地提升了舰船的火力打击与毁伤防御能力。但与此同时也暴露出一些问题:一是“可靠性水平”未能同步升级换代,主要体现在部分新研制的导弹系统在入役初期故障率较高;二是驻舰官兵对新型舰载导弹系统的操作与维修技能缺乏学习培训,经常因操作不当造成故障,同时舰员也不具备排除新型舰载导弹故障的能力;三是舰载导弹的保修期短,当前舰载导弹随同整舰享受一年的初始保修服务,也称为质保服务,保修任务及成本由造船厂承担。但当前“一刀切”的初始保修服务并不能使舰载导弹,特别是新研制新型号舰载导弹在保修期内暴露造船厂责任故障问题,一年保修期到期后,舰载导弹无论出现任何故障,都必须由军方自行修理。例如,某新舰在出厂服役4～5年后,导弹相继出现质量问题,属于承制方责任故障;某舰的导弹发射系统入役3年后第一次实际使用时发生承制方责任故障,但2个故障均超过了一年保修期,船厂拒绝保修。因此,有军内专家认为当前我海军实行的舰载导弹及舰船保修制度早已不能达到质量保证的效果,应展开相关研究、深入论证,对舰载导弹及舰船保修制度做出优化调整。

现有对舰载导弹系统保修期的研究主要从采购案例分析、合同条款优化、军地权益博弈等角度进行展开,定性论证了调整舰载导弹系统保修期的必要性。对舰载导弹系统保修期采用以军方需求为导向的经验判断来确定,对承制方不具有说服力。文献[13]提出了商品保修期优化的分析思路,构建了商品全局最优保修期模型,但在实证分析上较为薄弱,且其为双目标线性规划函数,主要计算消费者和生产商效益同时最大时的保修期,在约束条件下，无解的可能性较大且计算困难,模型的应用与可操作性存疑。文献[14]构建了商品公平保修期模型,通过实例分析得到对消费者和生产商权益均等的公平保修期。但商品与装备在可靠性规律、效益属性、价值体量等多方面存在差异,不能简单套用。且其对商品故障率的设定较为随意,缺乏必要的解释说明。文献[15]和文献[16]分别提出了机床、汽车等商品的故障责任数据处理方法,为挖掘舰载导弹系统的故障规律,确定其故障率函数形式与参数提供了思路。综合以上问题,现有研究存在的不足为:① 缺乏对舰载导弹系统保修期优化的定量研究思路;② 缺乏能够满足舰载导弹系统保修期优化研究的模型;③ 舰载导弹系统责任故障数据信息没有被充分利用。

针对此问题,使用线性回归法判断舰载导弹系统责任故障数据更拟合哪一类故障分布函数(指数分布函数、极值分布函数、威布尔分布函数、正态分布函数与对数正态分布函数),并求出舰载导弹系统故障率函数及参数。再根据舰载导弹系统作为军用装备的特点,分别优化了文献[13]和文献[14]提出的全局最优保修期模型与公平保修期模型。最后,通过算例数据计算求解,得到符合预期的公平保修期,并可根据全局最优保修期的解,判断分析舰载导弹系统保修期的优化方向。

1 舰载导弹系统故障率曲线定量化建模

舰载导弹系统保修研究的最终目标是制定最优保修策略,推进一体化维修与提升舰载导弹系统的可靠性,评价寻优需要建立在大量建模与仿真分析的基础上,而其中舰载导弹系统故障规律是模型的基础与仿真的重要参数。许多国内研究学者使用国外的研究成果,往往简化假设舰船大致服从某分布、某参数的故障规律,建模基础不符合实际,导致保修费用、成本模型脱离实际、仿真求出的最优解科学性存疑,进一步影响保修方案选择的正确性。因此,舰载导弹系统早期故障数据的分布规律研究首当其冲。而线性回归拟合是分布规律研究最有效、可操作性最强的分析方法。

1.1 筛选责任故障数据

早期故障数据多为责任故障数据,中华人民共和国船舶行业标准CB1379 2《舰船产品可靠性试验故障分类》中将可靠性试验中的舰船故障进行了分类,其中关联故障主要由设计缺陷、制造工艺缺陷或零、部件及元器件缺陷造成。关联故障中,研制或生产组织责任范围内的原因引起的关联故障应判定为责任故障。

在舰船舰载导弹系统故障资料中筛选出由于研制或生产责任导致的责任故障,并按照故障部位分类,将发生故障日期距交付日的天数作为责任故障数据。

1.2 建立回归模型

设为故障数据的序数,∈{1,2,3…,};故障距始时间记为,单位为“天”记为d,同时,通常采用中位秩法估测计算分布函数值:

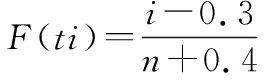
(1)

在可靠性试验中最重要的方法为回归分析法,即对常用的故障分布函数进行线性变换,转化为线性回归方程:

=+

(2)

式中:多个(,)故障记录数据点可粗略拟合在一条截距为,斜率为的直线附近。

1.3 故障分布类型

保修数据分析中常用的故障分布有5类:指数分布、极值分布、威布尔分布、正态分布与对数正态分布。

131 指数分布

指数分布是韦伯分布的一种特定形式,舰船电子部件的故障规律大多服从指数分布。双参数指数分布的分布函数为

()=1-exp[-(-)]

(3)

式中:为尺度参数;为位置参数。将两端取对数,得回归方程为

(4)

132 极小值分布

极小值分布常用于描述类似死亡率、旱季降雨量等极小值的概率分布,舰船局部腐蚀等多服从极小值分布。极小值分布的分布函数为

(5)

式中:为尺度参数;为位置参数。整理后得回归方程:

(6)

133 威布尔分布

威布尔分布是可靠性研究中最常见、最重要的分布,因此舰船上的众多通用设备的故障规律大多服从威布尔分布。常用两参数威布尔分布的分布函数为

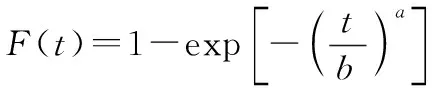
(7)

式中:为形状参数;为尺度参数。整理后得回归方程:

(8)

134 正态分布

正态分布广泛存在应用于生活中,舰船上的橡胶制、机械产品等故障规律大多服从正态分布。正态分布的分布函数为

(9)

式中:为均值;为标准差。接下来对其标准化,令=0,=1,整理后得回归方程:

(10)

确定()

首先,通常采用中位秩法估测():

(11)

求解

当0<()<05时,=();当05<()<1时,=1-()。

求解

=-ln(4(1-))

(12)

求解

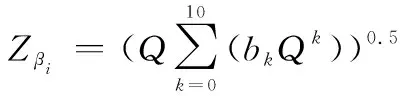
(13)

式中：,∈{0,1,2…9,10}根据中国科学院计算中心概率统计组发布的正态分布多项式近似公式确定。

=0157 079 628 8×10;

=0370 698 790 6×10;

=-0836 435 358 9×10;

=-0225 094 717 6×10;

=0684 121 829 9×10;

=0582 423 851 5×10;

=-0104 527 497 0×10;

=0836 093 701 7×10;

=-0323 108 127 7×10;

=0365 776 303 6×10;

=0693 623 398 2×10

确定

(14)

正态分布转化回归方程后对应的、值

135 对数正态分布

对数正态分布则是随机变量的对数服从正态分布,舰船的结构、金属疲劳等往往服从对数正态分布。对数正态分布的分布函数为

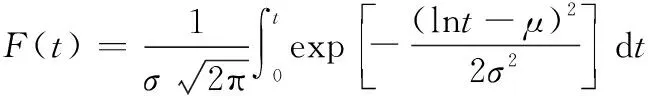
(15)

式中:为均值;为标准差。接下来对其标准化,令=0,=1,整理后得回归方程:

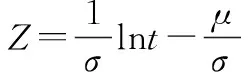
(16)

同理正态分布,因变量的值与正态分布所转化的值相同,即

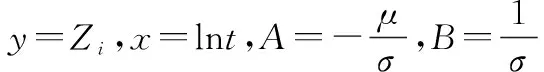
1.4 决策与求解

当分别转化求出五类分布对应的保修数据和后,利用与之间的相关系数(∈[0,1])的大小判定最优分布类型,求解相关系数。

相关系数利用统计软件SP.SS_26.0求得,且可以在给定显著性水平、样本量的前提下,通过查表找到相关系数的临界值[],若求出的>[],则认为经过对应分布转化后的与是线性相关的,该保修故障数据服从此类分布,且越大,越接近于1,线性相关性越强,对应分布的拟合效果越好。

令威布尔分布转化数据计算出的相关系数记为,指数分布转化数据计算出的相关系数记为,极小值分布转化数据计算出的相关系数记为,正态分布转化数据计算出的相关系数记为,对数正态分布转化数据计算出的相关系数记为。

1.5 现场数据分析

151 现场数据筛选

经调研海军舰入役5年间舰载导弹系统的维修记录(故障原因及类型、故障日期),筛选出其中在研制或生产组织责任范围内的故障,根据故障的发生日期及该舰的交付日期计算故障距始时间,单位为“天”(d),得到保修数据如表1所示。

表1 舰载导弹系统现场故障数据

1.5.2 线性回归解析与相关系数对比

经统计软件SP.SS_26.0求解,在显著性水平=0.05的情况下,对于案例中X舰舰载导弹系统的责任故障数据,各分布类型线性回归转化后的自变量和因变量,及二者之间的相关系数如表2所示。经查相关系数临界值表,在显著性水平为=005,=-2=16的相关系数临界值[]=0468 3。

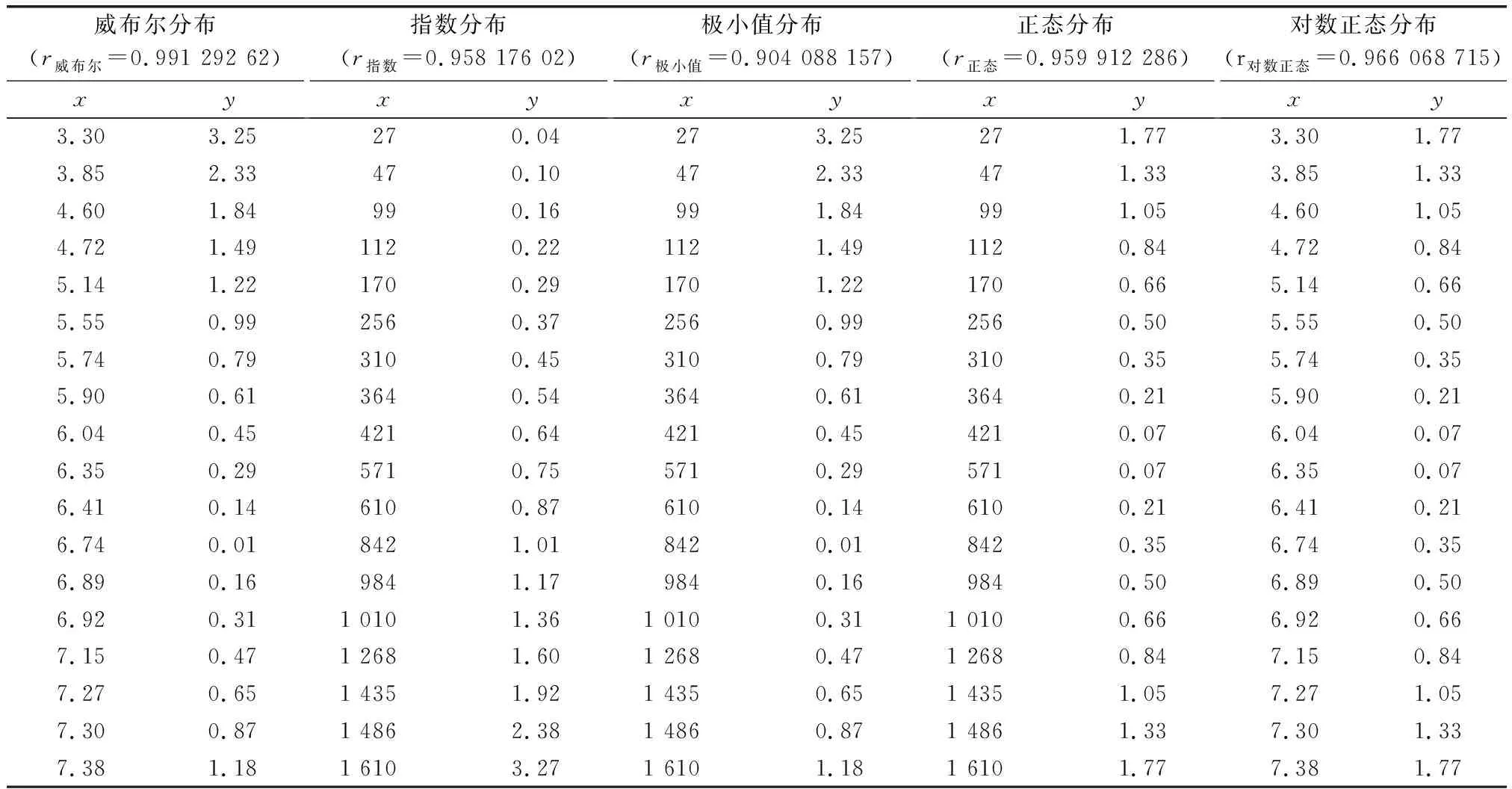
表2 5类分布线性回归参数与相关系数

5类分布中,相关系数均大于[r]=0.468 3,且相关系数最大的为r=0.991 292 62,因此认为威布尔分布的回归拟合效果最好。

1.5.3 舰载导弹系统的可靠性函数求解

现利用统计软件SP.SS_26.0对威布尔分布转化的故障数据进行线性回归,回归结果如表3及图1所示。

表3 威布尔分布转化的舰载导弹系统故障数据回归统计表

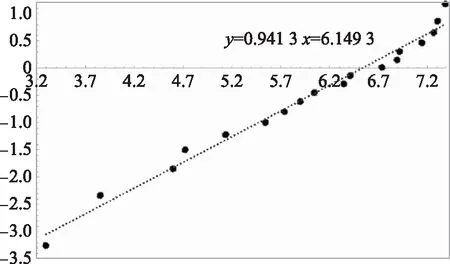
图1 威布尔分布转化的舰载导弹系统故障数据回归拟合图Fig.1 Regression fitting diagram of shipborne missile system fault data transformed from Weibull distribution

查表得1-(1,-2)=1-005(1,16)=449,=906778 356 7≫449=1-(1,-2),即说明在显著性水平为005的情况下,威布尔分布转化的舰载导弹系统故障数据线性回归效果显著。且可由表4获得威布尔分布转化后舰载导弹系统故障数据的回归系数,=-ln=-6149 3,==0941 3,计算得到威布尔分布的双参数为=0941 3、=687106 3,代入式(7)中,实例中舰载导弹系统故障数据的分布函数为

表4 威布尔分布转化的舰载导弹系统故障数据回归系数值表

154 故障率函数与检验分析

根据如下双参数威布尔分布的故障率函数：

(17)

将双参数代入式(17)中,得到实例中舰载导弹系统故障数据的分布函数为

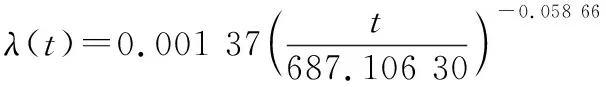
绘制故障率函数曲线如图2所示。根据图2,案例中的舰载导弹系统在服役的20年内故障率总体上由高到低递减,且递减速率逐渐减慢。具体来看,案例中的舰载导弹系统在前50天的故障率迅速锐减20%,第一年的故障率迅速锐减30%,第2～4年的故障率下降趋于缓慢,3年间约下降约7%,第4年开始下降趋势不再明显,基本维持在=0001 2～0001 3,即012%～0.13%的故障概率水平,即将结束早期故障期,进入故障率稳定的偶然故障期。与基层部队调研反馈的舰载导弹系统早期3～5年左右故障高发时段相差不大。

图2 基于现场数据参数的舰载导弹系统故障率函数图Fig.2 Failure rate function of shipborne missile system based on field data parameters

下一步对现场数据解析结果进行拉普拉斯检验。拉普拉斯趋势检验又称“截尾检验”,可以判断舰载导弹系统是否出现可靠性的变动,验证二参数威布尔分布所拟合的模型趋势是否正确,其统计量定义为,计算公式如下:

(18)

式中:为样本总量,即最大值,在本案例中为18;为区域总时间,在本案例中为1 825 d(5年)。

令显著性水平为,则会有2个判定临界值,2与1-2,∈(-∞,2),可靠性在该区域增长;∈[2,1-2],可靠性没有明显变化,且越接近于0,越可以判定该区域的可靠性没有任何变动趋势;∈(1-2,+∞),可靠性在该区域下降。

令显著性水平=005,查阅拉普拉斯趋势检验值临界表可得0025=-196、0975=196;令显著性水平=010,查阅拉普拉斯趋势检验值临界表可得0025=-1645,0975=1645。

根据表5的计算结果可知,无论在005还是01的显著性水平下,舰载导弹系统在182 5 d(5年)内有显著的可靠性增长趋势。

表5 拉普拉斯趋势检验计算参数表

本检验结果既与前文所示的二参数威布尔分布下舰载导弹系统故障率曲线趋势相吻合,又与先期调研中了解的部队舰船故障发生特性吻合。因此,用二参数威布尔形式拟合舰载导弹系统现场故障数据得出的故障参数符合部队实际,模型较为正确地解析了舰载导弹系统的故障规律。

2 舰载导弹系统优化保修期研究

舰载导弹系统作为舰船的重要组成部分,享受造船厂提供的一年保修期服务。但从前文现场数据的故障特性来看,舰载导弹系统在入役初期要经历3～4年的高频故障期才能达到稳定的可靠性水平,且此类故障均为由设计缺陷、制造工艺缺陷或零、部件及元器件缺陷造成的承制方责任故障。根据求出的舰载导弹系统故障率函数,可以估测出舰载导弹系统在一段时间内的故障次数,在维修费用一定的条件下,无论保修期的长短,时间区域内的维修费用是必然发生且确定的。从军方角度讲,希望造船厂提供终身保修,承担所有的维修任务与成本;从承制方角度讲,其希望能尽快终止保修义务,由军方自主承担维修任务与成本。保修期过短会使舰载导弹系统的承制方责任故障无法全然暴露,影响载导弹系统的可靠性和战舰的战斗力,军方权益受损;保修期过长意味着增加承制方售后成本,侵蚀承制方利润,必然影响承制方和军方的合作关系。因此,确定一个公平合理的保修期应平衡承制方和军方的利益,以此制定目标函数,用双方利益底线设置约束条件,解出保修期。

2.1 模型假设

在构建目标函数前,为简化模型计算难度,需要做出如下假设。

舰载导弹系统发生责任故障后,采取的维修方式为非更新维修。即在故障发生时,通过维修仅使故障部位恢复至发生故障前的状态,而非直接更换部件。非更新维修也不需重新计算保修期,便于模型的简化计算。

舰载导弹系统采取一维的保修策略,即衡量保修期长短的期限仅由日历时间确定,而二维保修策略的期限一般由日历和使用强度(如里程,转数等)共同决定,目前无论是舰船保修领域还是导弹保修领域均未成功引入二维保修模式。假设在舰载导弹系统建模中使用的时间单位为天,即舰载导弹系统作为舰船火力的重要保障系统,需要保持高水平的可用度,全天候在位。

舰载导弹系统采取保修期内免费的保修策略,即在保修期内所有修理费用由承制方承担。除免费保修策略外,军方与承制方还可协商对保修期内的维修费用实行按比例分摊或折扣分摊的方式由双方共同承担,属于购买“延保服务”决策研究,不在本文的研究范畴内。

舰载导弹系统在服役末期进入耗损故障期,不再为军方创造收益,因此假设舰载导弹系统在全服役期内(除去耗损期)的故障服从二参数稳定的威布尔分布。

为简化计算,假设舰载导弹系统每一次发生承制方责任故障时，军方与承制方均具备将故障部位恢复至发生故障前状态的能力,且维修能力在舰载导弹系统寿命期内不发生改变,但能力大小(维修时长及成本)各异。

假设由军方主导的定期修理不影响舰载导弹系统承制方责任故障的发生概率。本文重点研究舰载导弹系统承制方责任故障维修任务及费用的归属问题,因而假设在舰载导弹系统全寿命期内,除承制方责任故障导致的维修停工外其他所有的寿命时间均为可正常工作时间,产生工作收益与工作成本。

2.2 设定变量

设舰载导弹系统总合同价格为(单位:万元),全服役期(除去耗损期)为(单位:d),保修期限为(单位:d),承制方对舰载导弹系统的总成本(包含建造成本、销售成本、企业分摊进该产品的管理运营成本等)为(单位:万元)。

设承制方在保修期内对舰载导弹系统故障的平均每次维修时间为(单位:d),平均每次维修费用为(单位:万元)。

设军方在保修期外对舰载导弹系统故障的平均每次维修时间为(单位:d),平均每次维修费用为(单位:万元)。

且由于维修效率、学习曲线效应、劳动力价格及供应商资源等原因,一般<,<。

另外,设舰载导弹系统单位时间(d)为海军创造收益(单位:万元),舰载导弹系统单位时间(d)使用费用为(单位:万元),舰载导弹系统单位故障时间(d)使海军损失为(单位:万元)。

2.3 基于效益最大化的全局最优保修期模型

基于效益最大化的全局最优保修期是指分别建立承制方和军方对于舰载导弹系统的效益模型函数,以两个函数的和为目标函数,目标函数最大时对应的保修期(单位:d)即为能使双方效益最大化的全局最优保修期。

令承制方对于售卖及保修舰载导弹系统的效益为,军方对于购买、使用及维修舰载导弹系统的效益为。

计算平均故障及维修次数

计算

承制方对于售卖及保修舰载导弹系统的效益等于承制方总收益除以总成本。

基于模型假设,承制方对于售卖及保修舰载导弹系统的总收益为舰载导弹系统总合同价格为(单位:万元)。

总成本由管理运营成本(单位:万元)及保修成本组成,模型如下:

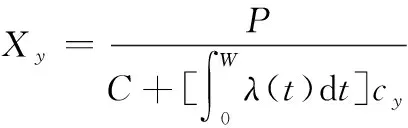
(19)

计算

军方对于购买、使用及维修舰载导弹系统的效益等于军方在舰载导弹系统可用时间区域内使用舰载导弹系统获得的总收益除以总成本。

基于模型假设,舰载导弹系统可用时间等于舰载导弹系统全服役期(除去耗损期)减去保修期内外承制方和军方排除故障所消耗的维修时间,再乘上舰载导弹系统单位时间为海军创造收益,即为军方在舰载导弹系统可用时间区域内使用舰载导弹系统获得的总收益。

其中,为使和尽量相等,舰载导弹系统单位时间为海军创造收益近似等于装备购买价格乘以5%的定额收益率再除以舰载导弹系统的工作在位天数(全寿命减去修理时间总和),再结合军地双方谈判意见予以浮动调整。修理时间总和可根据维修历史数据计算或按比例推算得出。

总成本包含4个部分,一是舰载导弹系统总合同购价;二是保修期外的故障维修费用,等于保修期外故障次数乘以军方平均每次维修费用;三是军方在舰载导弹系统可用时间区域内使用舰载导弹系统的费用,等于舰载导弹系统可用时间乘以舰载导弹系统单位时间使用费用;四是舰载导弹系统在故障期间因无法执行任务给军方带来的损失,等于舰载导弹系统保修期内外故障时间总和乘以单位故障时间损失。军方购买、使用及维修舰载导弹系统效益的模型如下:

(20)

基于效益最大化的全局最优保修期模型

令=+,则目标函数为

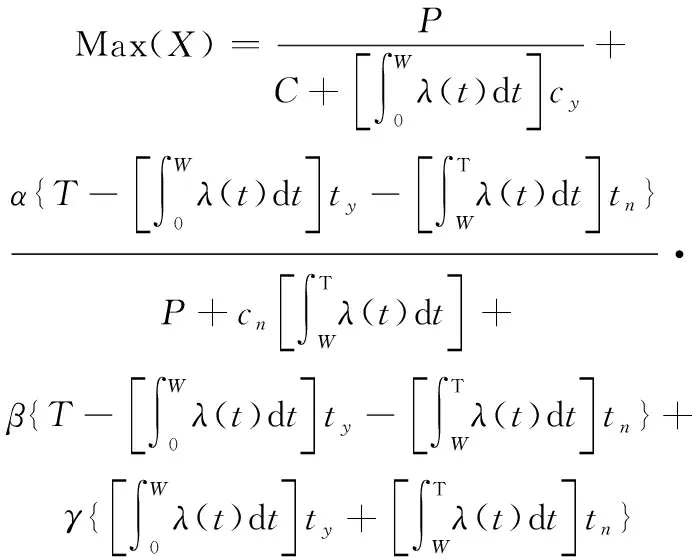
(21)

目标函数的含义为,以承制方和军方对于舰载导弹系统的两个效益模型函数的和为目标函数,目标函数最大时对应的保修期即为能使双方效益最大化的全局最优保修期。

约束条件为

(22)

约束条件的含义为,首先保修期必须大于0且小于舰载导弹系统的全寿命期,另外承制方售卖及保修舰载导弹系统的效益和军方购买、使用及维修舰载导弹系统的效益均须大于1,即承制方不会因保修造成售卖舰载导弹系统亏本,军方也要保证自身购买和使用舰载导弹系统是效益大于成本的。

计算全局最优保修期

根据实地调研获取的资料或利用德菲尔法(专家咨询)确定除 “保修期”外其他所有设定量的值,带入目标函数及约束条件函数模型,得到自变量为保修期,因变量为的线性规划函数,可解出Max()时对应的保修期记为,即为基于效益最大化的全局最优保修期解。

2.4 基于效益均等化的公平保修期模型

基于效益均等化的公平保修期是指分别建立承制方和军方对于舰载导弹系统的效益模型函数,以两个效益模型相等函数为目标函数,在约束条件范围内直接求解若可以得到保修期(单位：d),即为能使双方效益均等化的公平保修期。因此，可利用前文构建的承制方和军方的效益模型、。

基于效益均等化的公平保修期模型要求两个效益模型相等,因此可直接构建如下方程,并带入参数求解,即使=。

(23)

根据实地调研获取的资料或利用德菲尔法(专家咨询)确定除 “保修期”外其他所有设定量的值,代入式(23),利用Matlab等求解方程式。

若存在解,还需将解代入式(22)的4个约束条件中,若此解能同时满足所有的约束条件,即为基于效益均等化的公平保修期解,记作。

若此方程无解,或求得的解不能同时满足式(22)中所有的约束条件,则认为依据现有参数无法找到效益均等化的公平保修期,需要调整设定量的值。

2.5 算例分析

251 算例数据输入与求解

延用现场数据分析中的舰船舰载导弹系统的故障率二参数威布尔分布形式及参数:

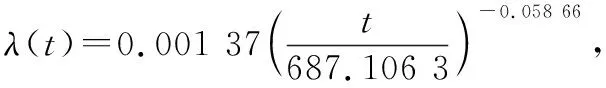
表6 X舰船舰载导弹系统算例数据

在Matlab2018b中分别输入2类保修确定模型的方程与算例数据进行线性规划求解,采用单目标规划求解算法及方程求解,输出相关参数结果如图3所示。并整合保修期一年时的相关参数结果作比较,如表7所示。

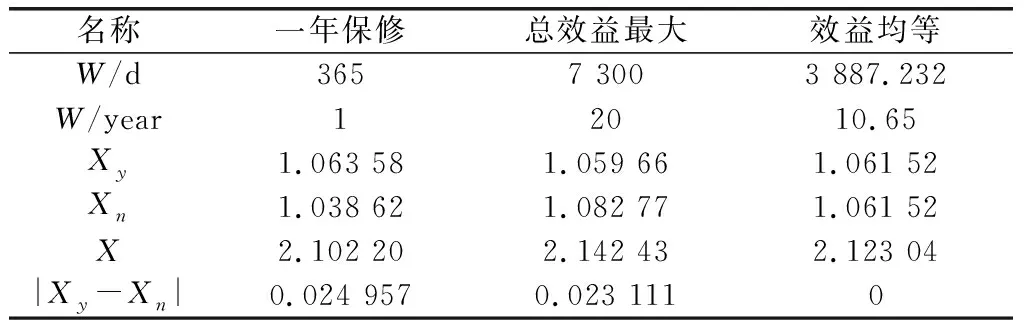
表7 3种同保修期方案的效益值

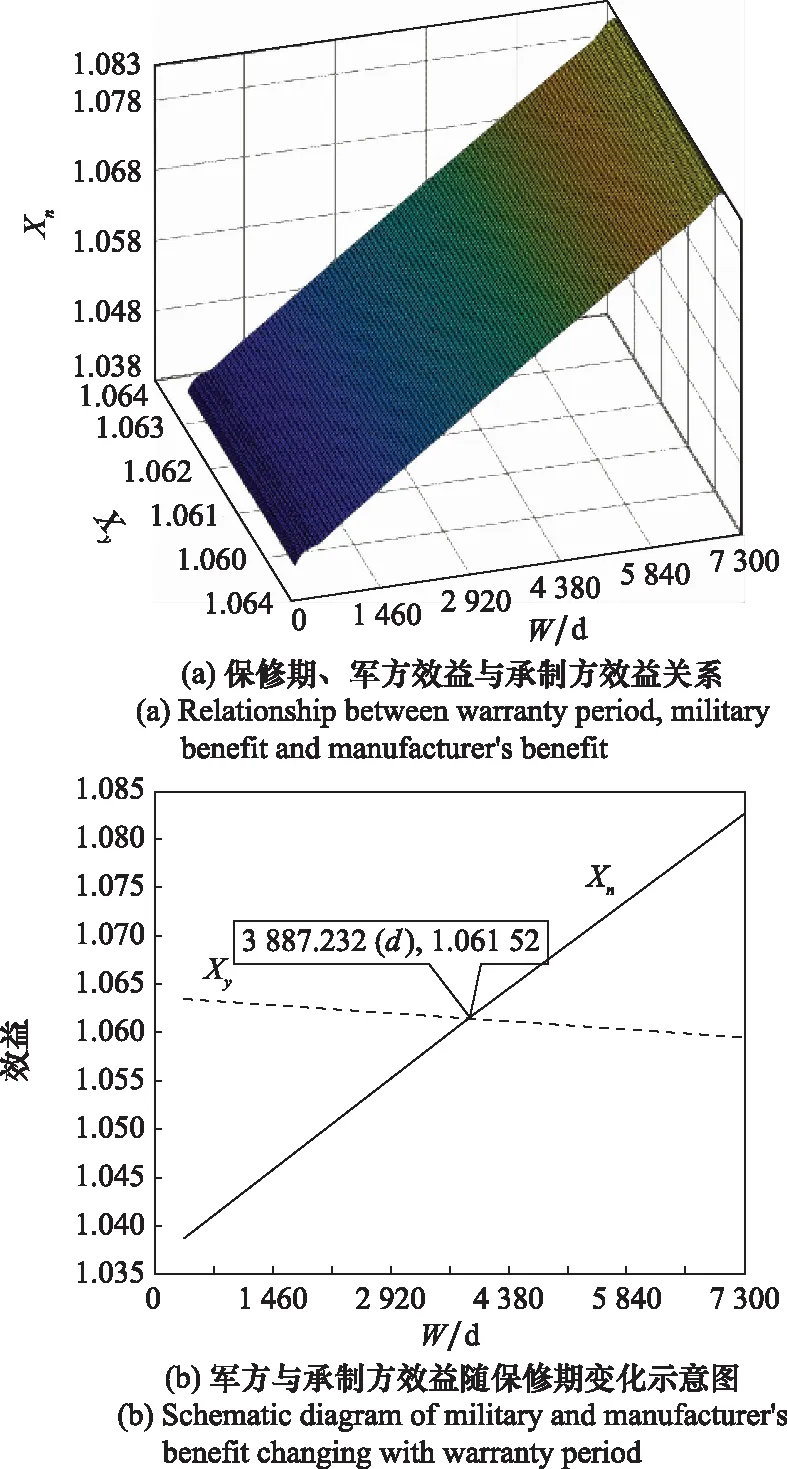
图3 基于算例数据的保修期、军方效益与承制方效益三变量关系图Fig.3 Three variable relationship diagram of warranty period, military benefit and manufacturer benefit based on example data

2.5.2 基于效益最大化的全局最优保修期算例解分析

如图3(c)所示,当=7 300 d时,=Max()=2.142 43,此时,=1059 66,=1.082 77。即当保修期等于舰载导弹系统的寿命时长时,承制方与军方的全局效益最大。

承制方的利润率约为5.97%,高于装备采购制度调整改革前承制方5%的合同利润率,未对承制方最基本的利润率产生侵蚀。军方利用舰载导弹系统的军事利润率约为8.28%。相较于传统的一年保修期,承制方的利润率仅下降6.17%(6.36%→5.97%),而军方的利润率则上升了114%(3.86%→8.28%),军方与承制方的效益值和X也达到了模型约束条件下的最大值Max()=2.142 43,实现了双方全局最优的目标。

由此分析,在军方和承制方对舰载导弹系统承制方责任故障维修能力在寿命期内不变的假设下,承制方由于积累了大量建造和研改舰载导弹系统的经验,排除舰载导弹系统承制方责任故障的时间更快、成本更低。如图3(b)所示,承接保修任务和成本对承制方利润率的侵蚀斜率小于对军方收益率的削减斜率。

基于效益最大化的全局最优保修期对承制方产生了显著的不公平倾向,直接将双方的效益差额正负扭转(-:0.025→-0.023),在合约谈判中,理性的承制方不会接受此保修期方案,但却启迪了军方去进一步研究是否可以通过购买承制方的有偿延长保修服务提升自身的利益杠杆,同时使全局效益最大化。

2.5.3 基于效益均等化的公平保修期算例解分析

如图3(b)中两线交点及图3(c)中虚线所示,当=3 887.232时,==1.061 52。即当保修期等于10.65年时,承制方与军方的效益均等。

基于效益均等化的公平保修期相较于传统的一年保修期(军方力图调整变革)和基于效益最大化的全局最优保修期(理性的承制方不接受),军方和承制方更容易接受。一方面,相较传统一年保修期,对承制方的利润率侵蚀度不大,仅下降3.24%(6.36%→6.15%),且公平保修期下承制方的利润率仍高于装备采购制度调整改革前承制方5%的合同利润率,企业盈利正常;另一方面,公平保修期能使军方的利润率增加59.28%(3.86%→6.15%),军方购买使用舰载导弹系统的效益提升过半,也必然会赞同公平保修期;最后,公平保修期使军方和承制方的采购(销售)效益均等化,不对任何一方产生利益偏向,在不受其他环境变量影响的情况下,有利于双方迅速达成售后权责调整协议,优化舰载导弹系统的保修期。因此,军方和承制方对基于效益均等化的公平保修期接受度和认可度更强,同时也可根据现场协议谈判局势的优劣对公平保修期进行幅度调整,以达到谈判目标,可操作性与应用性更强。

3 结 论

舰载导弹系统是战舰完成火力打击和舰体防护的重要武器系统,一旦发生故障,战舰将成为海面上的活靶子,影响军事任务的完成,在战时或扭转局势,因此应高度重视舰载导弹系统的可靠性。本文对优化舰载导弹系统保修期研究做出如下3点创新成果。

(1) 利用线性回归拟合出舰载导弹系统的故障率形式与参数

文章基于中科院计算中心概率统计组建议的线性回归方法对舰载导弹现场故障数据进行5种分布形式的拟合,确定出相关系数最高的分布类型并计算出故障率参数,可操作性强,拟合成果符合预期与实际。

(2) 建立了基于效益最大化的全局最优保修期模型

文章结合前文得出的舰载导弹故障率函数建立了基于效益最大化的全局最优保修期模型。该模型建立在一维免费非更新不重新计算保修期等假设的基础上,以军方和承制方效益值的和最大为线性规划目标, 重点探求在舰载导弹寿命期内承制方责任故障次数已知的情况下,军方和承制方怎样分摊维修任务及成本能使双方的总体效益最大化。算例解方案虽然无法使承制方接受,但通过算例发现,承制方由于积累了大量建造和研改舰载导弹系统的经验,排除舰载导弹系统承制方责任故障的时间更快、成本更低,承接保修任务和成本对承制方利润率的侵蚀斜率远小于对军方收益率的削减斜率。因而军方可进一步开展购买承制方有偿延长保修期服务的研究。

(3) 建立了基于效益均等化的公平保修期模型

文章继续沿用军方和承制方的效益函数模型,建立了基于效益均等化的公平保修期方程模型。该模型同样建立在一维免费非更新不重新计算保修期等假设的基础上,以军方和承制方效益值相等为线性规划目标,重点探求在舰载导弹寿命期内承制方责任故障次数已知的情况下,军方和承制方怎样分摊维修任务及成本能使双方购买/出售效益均等化。通过算例发现,公平保修期均在双方接纳限度内,不侵蚀承制方基础利润率,还能较大幅度地提升军方的整体收益率,适于推广并引导保修期优化调整决策。

保修数据分析与建模是近年可靠性研究的前沿领域与后起之秀,是推升舰载导弹系统等武器装备可靠性不可忽视的重要研究方向。随着武器装备更新换代速率的持续加快,“向前端看”必将成为可靠性研究的新趋势,武器装备保修研究也将积流成渊,充分挖掘与调动承制方维修保障资源。