PMSM转速和转子位置的滚动时域估计器设计
2022-02-14卓陈祥杜锦才
卓陈祥,杜锦才
(1.无锡科技职业学院物联网技术学院,江苏 无锡 214028;2.浙江大学能源工程学院,浙江 杭州 310027)
高性能无位置传感器永磁同步电机(permanent magnet synchronous motor,PMSM)驱动控制策略中对于转速估计通常基于磁链估计器[1]和反电动势观测器[2],前者简单易行,但鲁棒性欠缺,而后者则只较适用于表贴式PMSM,内埋式PMSM则需要辅以其他计算实现。此外,还有基于模型参考自适应观测器[3]和滑模观测器[4]的转速估计方案,但前者存在收敛验证问题,后者动态响应较快但需应对抖振。最近,基于扩展卡尔曼滤波器(extended Kalman filter,EKF)的转速估计方法也发展趋于成熟[5-6],但复杂度高。对此,文献[7-8]将滚动时域估计器(moving horizon esti-mator,MHE)用于感应电机转子位置估计,取得了良好的估计精度,但求解过程略显复杂。MHE的优势主要体现在:状态选择使得MHE能够获得一些线性系统的优势,而非完全的非线性系统处理方式,从而降低了复杂度;此外,MHE方案所需的采样频率低,即以较少的信息获取来实现非常准确的转速和转子位置估计。
综上,本文将MHE方法应用于PMSM驱动系统中估计转子位置,从而构建无位置传感器系统。首先,分析了不同时域尺度下MHE的性能,探明了估计误差、计算负担和时域尺度之间的关系,从而得到了MHE的基本设计标准和可行性;然后,在估计精度方面与EKF进行了仿真和实验对比;进一步,搭配了两种不同的电流控制器来使用MHE,即传统PI控制器和模型预测控制器(model predictive control,MPC)[9];最后,实验结果还验证了10 kHz采样率下的MHE实时可行性。
1 PMSM数学模型


2 MHE设计
2.1 MHE原理
MHE的报道最早可见于文献[10],随着数值优化计算发展和嵌入式芯片计算能力的提高,其关注度越来越高。图1为时域尺度为N的滑动时间窗口。
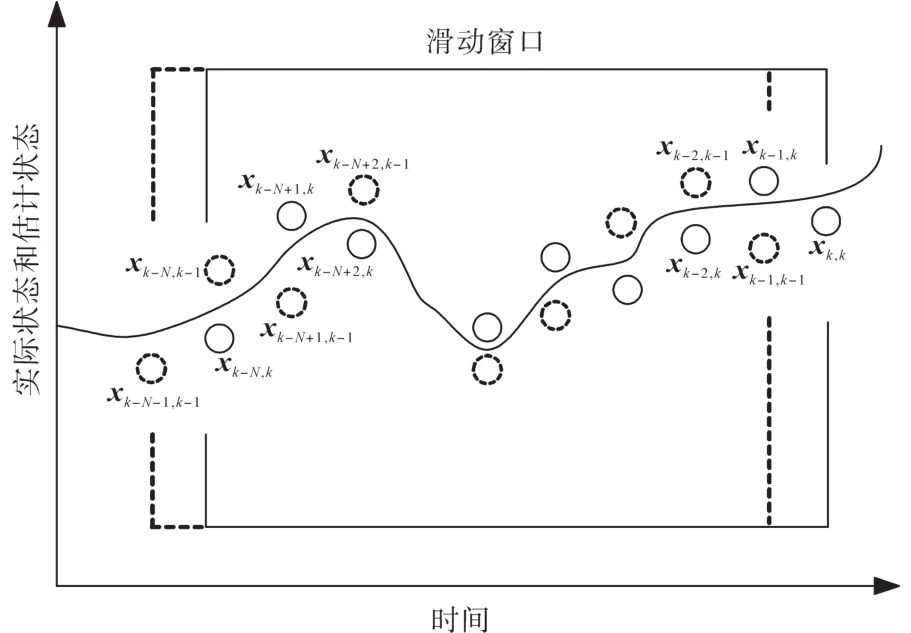
图1 滑动时间窗示意图Fig.1 Schematic diagram of moving time window


2.2 PMSM的MHE设计


2.3 MHE的实时实现


2.4 MHE与EKF的区别
EKF的原理为采用Taylor级数展开实现非线性问题向线性化逼近,然后进行卡尔曼滤波实现的状态估计。应用于无位置传感器PMSM驱动系统时,可选取定子的电压作为输入向量,定子电流作为输出向量,选取定子磁链、电机转速和转子位置为状态变量,从而由EKF观测定子磁链和电机转速。其存在的问题在于当系统非线性较强时与局部线性假设违背,Taylor展开式中被忽略的高阶项将带来较大的误差,从而EKF算法中滤波可能发散。此外,EKF在线性化处理时需要用雅克比矩阵,计算过程繁琐导致EKF实现相对困难。
MHE算法通过在滚动时间内调整模型的初始状态以及参数,让估计结果接近量测结果。MHE是以有限时间区间内,对程序模型及量测的最优化为基础的。在适当假设下,MHE就是一种含等式约束的二次规划类最优问题迭代求解算法,不需对非线性系统进行近似线性化处理,这和EKF有本质区别。因此,可以克服EKF算法中局部线性假设的缺陷。同时,在应用于无位置传感器PMSM驱动系统时,其计算负担小于EKF。但MHE可与EKF因为都是对系统状态估计,在数学上也存在一些关联性。
3 仿真分析和计算
为验证前述设计的MHE,在Matlab/Simulink仿真平台中进行了仿真测试。
仿真模型中采样周期为100 μs,时域尺度N=10,其中PMSM的主要参数为:定子电阻R=1.9 Ω,同步电感L=3 mH,极对数P=4,额定转速ωn=2 000 r/min,转动惯量Jn=0.000 18 kg·m2,永磁磁链ΨPM=0.1 Wb。
图2为基于MHE的PMSM无位置传感器驱动系统控制框图,电流控制器可采用PI控制器或MPC控制器。转速控制外环采用常规PI调节器实现。由于MHE算法主要适用于PMSM中高速运行时的转子位置估计,故PMSM低速运行时采用了常规的开环V/F控制,即保持V/F之比为常数,以期在低速时保持恒定磁通,当转速升高至中速运行后切换至基于MHE算法的转速闭环控制。
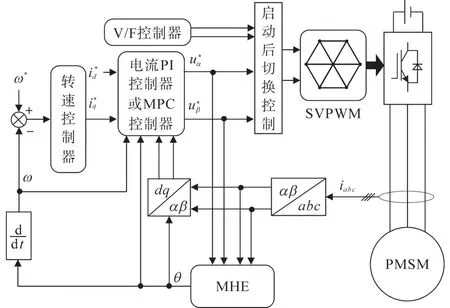
图2 基于MHE的PMSM无位置传感器驱动系统控制框图Fig.2 Control block diagram of PMSM rotor position sensorless drive system based on MHE
为了突出MHE的优势,将MHE与经典的EKF[5]进行了对比仿真,主要考察两者的转速和转子估计精度和动态。图3为仿真结果,仿真中设置t=0 s时转速控制器输入转速参考ω*从0阶跃至1 000 r/min,t=1 s时突加负载转矩。
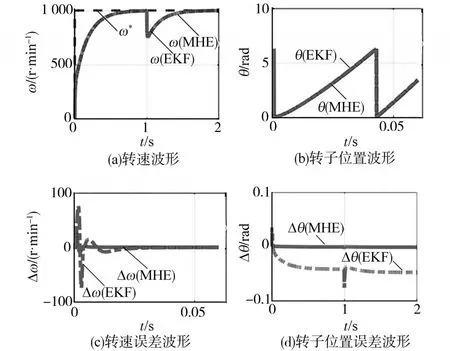
图3 MHE和EKF对比仿真结果(N=10)Fig.3 Comparison of simulation results between MHE and EKF(N=10)
由图3可以看出,MHE在稳态和动态下的转速和转子位置误差均小于EKF方案。值得注意的是,两种估计器得到的转子位置均存在稳态误差,这是由无限惯性假设引起的,但EKF的误差更为显著,也即表明简化假设对EKF极为不利。
进一步,通过仿真分析时域尺度N对MHE的影响。图4为设置N=2的仿真结果,其与图3(N=10)的结果基本一致。由此可得,窗口长度在MHE应用于PMSM驱动系统的影响主要在于收敛速度,N取值越大,则收敛越快,适用于低速区,但对应计算量越大,故实际中可酌情减小N。分析系统模型可发现存在两个时间点约束,即步长k和步长k-1,故N=1可对系统求解,但设置N=2则可更快速地收敛到精确解。有趣的是,图3和图4中EKF仿真结果也有所不同,这是由于协方差矩阵参数变化而引起的。
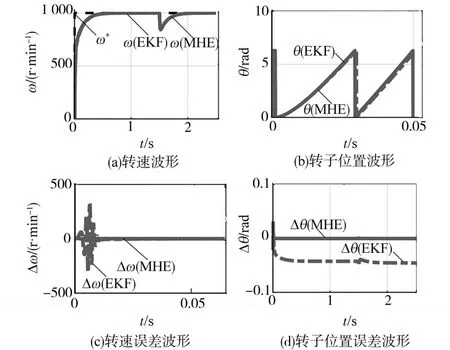
图4 MHE和EKF对比仿真结果(N=2)Fig.4 Comparison of simulation results between MHE and EKF(N=2)
4 实验验证
为深入验证所设计MHE的性能,开展了实验,实验平台主体为1台测试用PMSM和1台对轴安装的PMSM作为负载电机,其中PMSM参数与第3节相同。
基于MHE的PMSM无位置传感器算法基于实时仿真系统dSPACE(DS1104)实现,主频设置较低,为250 MHz,接近主流实时数字芯片的主频,以便于工业应用,例如TI公司的电机控制应用较为广泛的中性能Delfino浮点C2000系列芯片,主频达300 MHz,因此常规嵌入式系统即可应用本文提出的MHE算法。表1列出了运算时间明细,表中MHE中设置N=1和N=2的运算时间分别为12.4 μs和34.8 μs,有3倍差距,但总运算时间均小于采样周期100 μs,故开关频率可达10 kHz。

表1 控制任务运算时间统计表Tab.1 Table of calculation time of the control tasks
类似于仿真,实验也采用MHE(N=1)与EKF对比的方式进行,对比测试中仅改变转速估计器,转速和电流调节器的增益保持不变,这意味着两种估计器的带宽相同,同时驱动控制器速度外环已基于估计的速度闭合,并且旋转坐标变换已使用估计的转子位置执行。图5为ω*从500 r/min阶跃增至700 r/min,然后阶跃降至500 r/min的测试结果,图6为保持转速为500 r/min时突加负载扰动响应。对比动态测试结果可以看出,MHE产生的振荡较EKF小。
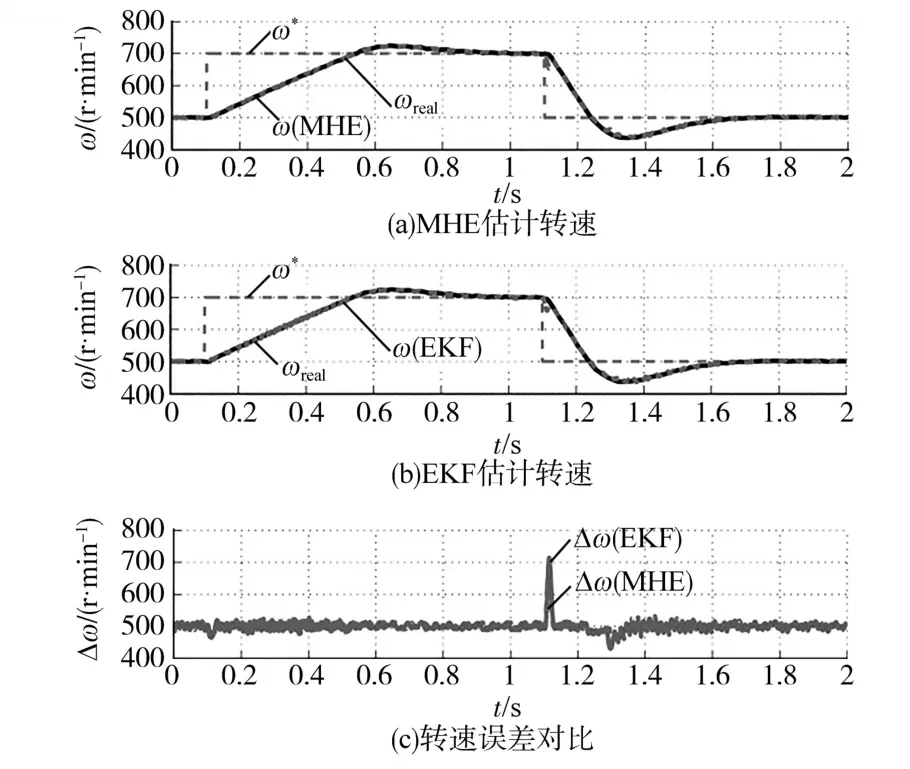
图5 转速阶跃测试结果Fig.5 Test results of the speed step
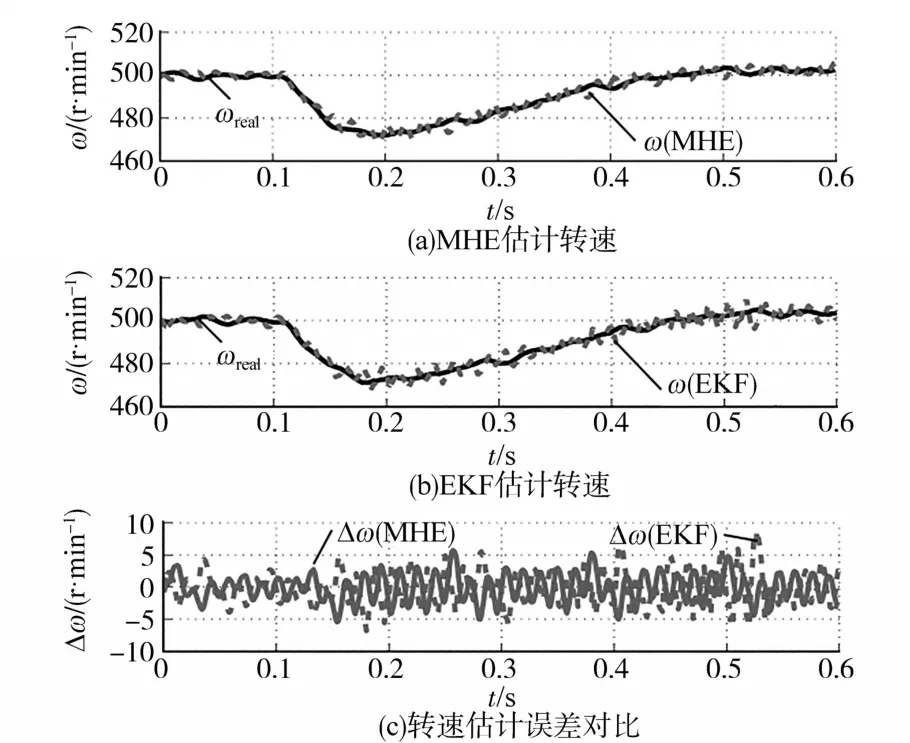
图6 负载转矩扰动测试结果Fig.6 Test results of the load torque disturbance
图7为稳态下,MHE与EKF所估计的转子位置和转子位置误差波形,对比结果显示,MHE稳态下估计的转子位置精度略高于EKF。为检验MHE的适应性,在前述采用电流PI调节器测试的基础上,用MPC取代PI调节器开展了进一步的对比实验,控制框图见图2。图8为电机转速为170 r/min时,MHE与EKF估计的转子位置误差对比,结果表明MHE比EKF在低速下的转子位置估计更为精确,更接近于零误差,而EKF则存在恒定的负误差。
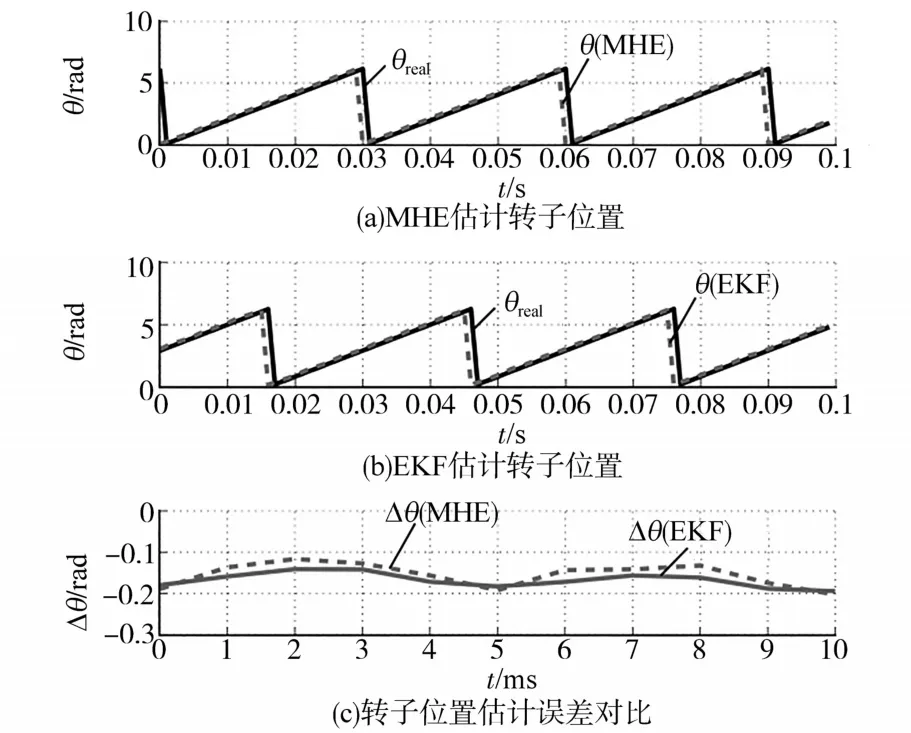
图7 MHE和EKF稳态对比测试结果Fig.7 Steady-state comparison of test results between MHE and EKF
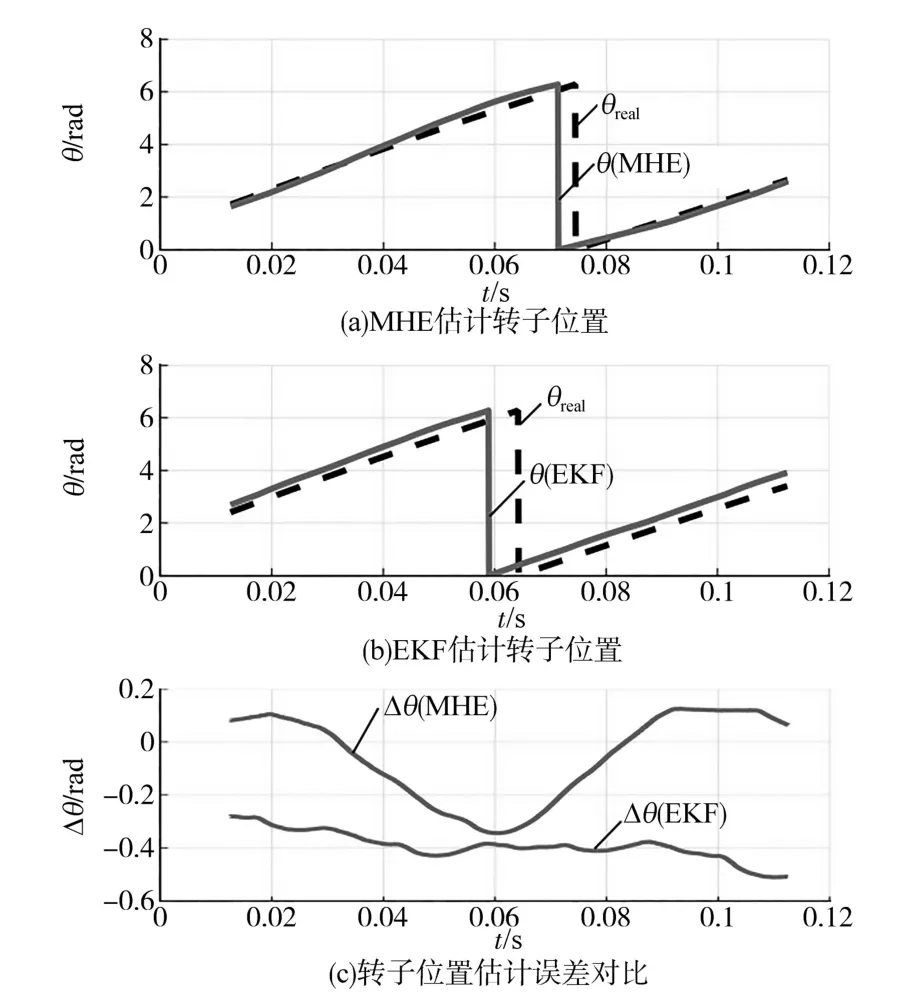
图8 低速测试结果(170 r/min)Fig.8 Test results of the low speed(170 r/min)
进一步降低电机转速到120 r/min,则MHE与EKF两种转速估计器误差均太大,导致系统失控,因此设置MHE中N=2再次进行降速测试,结果如图9所示,MHE的转速估计范围可低至70 r/min,说明MHE较之EKF的转速估计范围更宽。
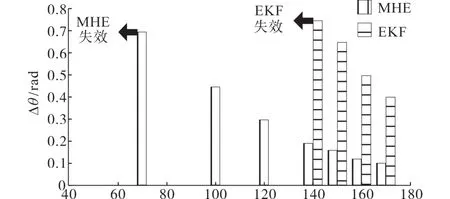
图9 MHE和EKF的转速适应范围边界对比Fig.9 Comparison of the boundary of MHE and EKF speed adaptation range
5 结论
本文设计了一种基于MHE的PMSM转子位置估计算法,现总结全文如下:
1)MHE本质上是一种适当假设下含等式约束的二次规划类最优问题迭代求解,基于离散时间域PMSM模型设计MHE后可通过摄动技术形成规范线性二次规划问题并得到实时求解,大大降低了计算负担;
2)MHE与EKF的对比测试结果表明,MHE在中高速下的转速和转子位置估计精度略好于EKF,但在低速性能显著更优,即转速估计范围较EKF更宽;
3)MHE可配合PI调节器或MPC调节器实施,效果俱佳,适应性好。
