离网型同步风力发电机单位功率因数新型控制策略

张思清，罗振鹏，石多峰，王淑玉，张志艳

（内蒙古工业大学电力学院，内蒙古自治区 呼和浩特 010080）

离网型风力发电主要为无电网地区的居民提供生活、生产所需的电力。此种情况下通常希望风机成本低并且使用寿命长，这可以从降低变换器容量和减少发电机损耗两个方面考虑。降低变换器容量最有效的方法就是在发电机发出有功不变的情况下将其发出无功控制为零，而减小谐波电流能大大地减小发电机损耗、增加其寿命[1-3]。所以本文将以单位功率因数控制和减小谐波电流两个问题为出发点进行分析。

在直驱永磁风力发电的机侧控制方法中，常规的最大转矩电流比控制，会在负荷功率增大时使无功功率快速增大，这对机侧变换器容量提出了更高的要求。针对这一问题，机侧变换器的单位功率因数是一个很好的解决方案，文献[4]利用传统的无功外环控制策略，能够实现单位功率因数控制，但是响应速度较慢；文献[5]提出通过控制电机d轴电压为零来实现永磁同步发电机的单位功率因数运行，此方法虽然能够实现单位功率因数运行，但在实际操作中比较复杂，尤其是在同步旋转坐标系定向时；文献[6]提出双静止坐标系下的单位功率因数控制，该控制方式结构简单，由于是在静止坐标系下对数据进行处理的，所以控制效果不如旋转坐标系下好。

若要实现变换器的单位功率因数运行，那么其电流谐波应该为零，但由于变换器自身特性、开关频率以及永磁同步电机自身缺陷等原因，电路中一定会产生相应的谐波电流，所以降低谐波电流也是单位功率因数控制的重要组成部分。文献[7-11]都有提出通过减小其输入、输出电流的谐波含量来降低电机损耗。为了减小谐波影响，文献[7]通过分析系统在5次、7次谐波时的数学模型，然后采用矢量比例积分（vector proportional integral，VPI）控制器来抑制谐波；文献[8]针对永磁风力发电机提出了一种非理想型的比例积分谐振（proportional integral-resonant，PI-RES）控制器来抑制发电机的电流谐波。

针对离网型永磁直驱同步风力发电机现有的单位功率因数控制的问题与不足，以及谐波电流对发电机损耗影响，本文设计了一种通过直接给出矢量控制下isd参考值的单位功率因数新型控制方法，并在此基础上引入PI-RES电流内环控制，以减小谐波电流，并给出了具体原理及参数设计。与传统控制方式相比，本文所设计的新型控制无功控制更加简单，在Matlab/Simulink中进行仿真实验，仿真结果显示：在运用PI-RES控制后发电机输出电流谐波得到了明显改善，与传统控制方式相比，其响应速度更快、无功波动更小，并且能够通过切换isd给定值调节发电机输出电压，验证了所提策略以及设计参数的合理性和有效性。

1 单位功率因数新型控制原理

当永磁同步发电机采用电动机惯例，即以输入电流为正时，则机侧变换器主电路结构如图1 所示，其中：esa，esb，esc为永磁同步发电机三相定子磁链感应电动势；isa，isb，isc为三相定子电流；Rs为定子电阻；Ls为定子电感与外串滤波电感的等效电感；usa，usb，usc为变流器相电压；RL为负载电阻；C为直流侧支撑电容；udc为直流侧电压；idc为直流电流；iC为电容充放电电流，iL为负载电流[4]。

图1 机侧变换器主电路结构图Fig.1 Main circuit structure diagram of machine side converter

假设d-q坐标系以同步速度旋转且q轴超前于d轴，将d轴定位于转子永磁体磁链方向上，得到按转子磁场定向的定子电压方程：

式中：usd，usq分别为同步发电机的d，q轴电压；Rs为定子绕组电阻；isd，isq为定子绕组d，q轴电流；Lsd，Lsq为发电机定子的d，q同步电感；ωs为同步转速；Ψf为转子磁链。

当忽略定子电阻时，由式（1）可得电机稳态电压方程：

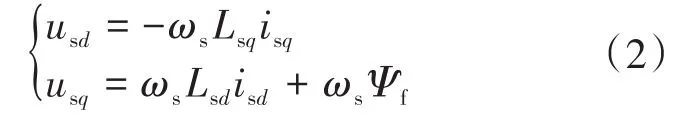
永磁风力发电机的有功功率Pgen和无功功率Qgen可表示为

将式（2）代入式（3）中可得稳态时发电机的有功功率Pgen和无功功率Qgen：

若要使发电机能够单位功率因数运行，就得让发电机无功功率为零，则由式（4）可得出：

而由式（4）可知isq与发电机有功功率有关系，所以只有通过调节isd来控制发电机输出无功功率，求解出式（5）的isd：

由式（6）可知，只有满足Ψf≥2Lsqisq系统才能正常工作；只要isd与isq满足式（6）关系，那么额定情况内，不论负载处于何种状态，均能实现发电机的单位功率因数运行；在任意一个isq值，即任意一种负载状态下，均有两个isd可以满足发电机的单位功率因数运行。

永磁同步电机的空间矢量图，如图2所示。其中：us为发电机定子电压，φ为功率因数角。

图2 电机空间矢量图Fig.2 Motor space vector diagram

由图2可知：在isq一定时，isd的两个结果都可以使功率因数角φ为180°。并且在取幅值较小的isd时，输出电压us的幅值Us会较大；在取幅值较大的isd时，输出电压us的幅值Us会较小。由变流器的运行特性可知，在空间矢量脉宽调制（space vector pulse width modulation，SVPWM）方式下，直流侧电压udc与交流侧电压幅值Us之间必须满足：

式中：m为调制比，且m＜1。

所以在系统满足式（7）的条件下，可选择幅值较小的isd作为给定；当系统不满足式（7）的条件下，可选择幅值较大的isd作为给定。如果用较小的isd作为给定，就会随着负载的增加而出现发电机端电压过高，而不满足式（7）的情况，工作范围受限；为了满足式式（7）通常使用恒端电压的控制方法，此时isd就不满足式（6）关系，也即变换器此时会有无功功率，在相同的负载情况下恒端电压控制就增加了变换器运行容量，而如果采用上述的单位功率因数控制就可以在保证单位功率因数的前提下降低输出电压，而不需要恒端电压的控制方法。这样就能够既减小变换器系统运行容量，又使系统的工作范围更广。另外由于isd的给定值是由isq运算后直接给出，不用经过外环控制环节，所以理论上系统动态响应速度会比传统无功外环控制更快、更稳，其控制效果更好。

2 控制系统设计

2.1 PI控制电流内环设计

由式（1）知变流器输出d，q轴电压相互耦合，因此可采用前馈解耦控制策略，当电流控制器采用PI控制器时，则usd，usq的控制方程如下[12-13]：

式中：Kip，Kii分别为电流内环比例调节增益和积分调节增益；分别为isd，isq的电流指令。

2.2 PI-RES控制电流内环设计

由于变换器自身特性、开关频率以及永磁同步电机自身缺陷等原因，在系统运行时同步电机输出的电流中含有较大的谐波，而大量的谐波会增加发电机的铜损与铁损，引起较大的转矩脉动，降低发电机寿命[4]。所以发电机电流谐波的抑制在电流环设计中尤为重要。

比例积分控制器能够实现直流信号的无静差控制，而比例谐振控制器能够实现交流信号的无静差控制。综合上述特点，文献[8]提出PI-RES控制器，来对永磁同步发电机的谐波电流进行抑制，其传递函数G（s）为[14-15]

式中：ωc为截止频率；h为谐波次数；Khwi为h次谐波谐振增益。

式（9）中的谐波传递函数可根据具体的情况进行适当的选取。根据式（1）和式（8）做出如图3所示的isq电流环结构，其中Ts为电流环采样时间，KSVPWM为桥路在SVPWM调制下的等效增益。isd电流环结构与其一致，不再赘述。

图3 电流内环结构Fig.3 Structure of the current inner loop

在不考虑扰动变量ωsΨf影响的情况下，将小时间常数Ts，0.5Ts合并，得到简化的电流内环结构，如图4所示。为实现电流环快速的跟随性能，可按照典型I型系统设计电流调节器。由图4可知，只需利用电流调节器的零点消掉控制对象的极点即可[16-17]，此时开环传递函数Giopen（s）为

图4 电流内环简化结构Fig.4 Simplified structure of current inner loop

由典型I型系统动态跟随性能指标和频域指标与参数关系可知，当阻尼比ξ=0.707时，有：

则可以求出Kip，Kii值为

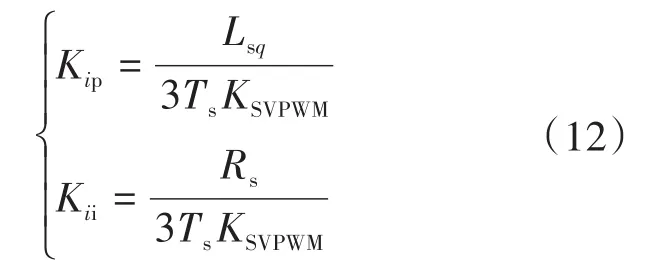
PI-RES控制中的比例系数Kp在PI控制器设计中已经确定，所以只能通过调节谐振增益Kwi与截止频率ωc来消除谐波信号。ωc的取值可根据电流波形的傅里叶分析来获取，波特图如图5所示。

图5 Kwi变化对比波特图Fig.5 Bode plot with different Kwi

假定ω=314 rad/s，ωc=10 rad/s，由图5可以看出通过调节Kwi可实现其幅频曲线向上或向下平移，既可影响控制器增益，又可影响控制器带宽，因此在理想情况下，合理的Kwi可以实现对被控交流谐波信号无静差调节，达到消除谐波的目的[8]。

2.3 PI控制电压外环设计

永磁直驱风电系统在离网状态下，直流侧的电压应由机侧变换器控制，发电机功率则由负载确定，所以外环控制变量为直流母线电压。同步旋转坐标系在基于转子磁场定向的条件下，主要通过调节q轴电流给定值控制直流侧电压稳定，调节d轴电流给定值控制无功功率为零。其中d轴电流给定值可按照式（6）选取，而q轴电流给定值则是电压外环输出值。

通过上述电流环分析，可得其闭环传递函数Gi（s）为

由变换器的数学关系得[13]：

式中：Im为线电流幅值。

由图1可知机侧变换器直流侧的数学模型为

则机侧变换器的电压外环控制结构如图6所示，其中τv为电压采样时间常数；Kvp，Kvi分别为电压环比例调节增益和积分调节增益[13]。

图6 电压外环结构Fig.6 Voltage outer loop structure

忽略扰动，将cos（ωst）取最大值1后，将电压调节器按照典型Ⅱ型系统设计，得出其电压外环开环传递函数Gvope（ns）：

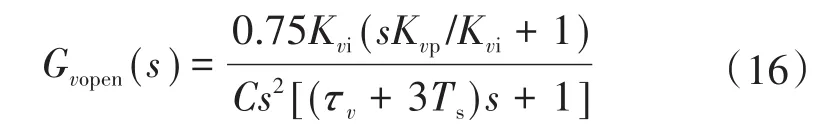
则电压环的中频带宽hv为

按照典型Ⅱ型系统的参数关系有：

考虑系统的跟随性和扰动性，工程上一般取hv=5，则可以求出Kvp，Kvi值为

3 仿真实验及分析

为了验证单位功率因数控制的正确性和控制器设计的可行性，在Matlab/Simulink中搭建了如图7所示的20 kW离网永磁风力发电机控制模型，其中，θ为转子的空间角度；np为磁极对数，ωw为风力机转速。

图7 离网型永磁直驱风电及其机侧控制系统Fig.7 The control system of stand-alone permanent magnet direct drive wind power and its generator side

仿真模型参数如下所示：风机额定功率Pw=20 kW，叶片半径Rw=5.25 m，额定风速v=10 m/s，空气密度ρ=1.225 kg/m3，直流侧电容C=0.5 mF，电机额定功率Pgen=20 kW，定子电阻Rs=0.000 2 Ω，定子电感Ls=5 mH，转子磁链Ψf=1.2 Wb，磁极对数np=8，转动惯量288 kg/m2。在设定电流与电压采样时间都为1×10-5s条件下，将上述参数代入式（12）、式（19）中可得：Kip=167；Kii=6.7；ωc=300 rad/s；Kvp=20；Kvi=300（考虑限幅作用，对参数进行了调节）；电压环限幅为-200～200。

3.1 控制结构频域分析

将上述参数代入控制结构中进行频域分析，通过分析开环和闭环波特图来验证电流内环和电压外环的参数设计，波特图如图8所示。

图8 电流环、电压环波特图Fig.8 Bode plot of current loop and voltage loop

通常希望网络结构的相位裕量为45°左右，此时系统则在满足稳定性的前提下而又不失其快速性。

由图8a、图8b可以看出，补偿前电流内环相位裕度为16.1°，补偿后相位裕度为23.1°；由图8c、图8d可以看出，补偿前电压外环相位裕度为86.6°，补偿后相位裕度为54.3°。所以按照典型Ⅰ，Ⅱ型系统进行设计的电流内环及电压外环闭环控制结构能够使系统快速稳定的运行，从理论分析上验证了参数设计的合理性。

3.2 PI-RES控制与PI控制对比仿真

设定仿真时间为0.3 s，风速v为10 m/s；负载PL为10 kW。由于0.15 s之前系统处于启动过程，所以取0.15～0.3 s时间的电流波形和傅里叶分析，PI控制仿真结果如图9所示。

图9 PI控制仿真结果Fig.9 Simulation results of PI control

由图9可知，电流环在PI控制下电流中含有较大的谐波，其中以5，7，11和13次谐波为主，总谐波畸变率THD为7.36%，所以在PI-RES控制中主要以抑制5，7，11和13次谐波为主，并调节谐振增益K5wi=35，K7wi=20，K11wi=12，K13wi=5，PI-RES控制仿真结果如图10所示。

图10 PI-RES控制仿真结果Fig.10 Simulation results of PI-RES control

由图10可知，电流环在PI-RES控制下电流中的谐波含量相较于PI控制中有所下降，此时总谐波畸变率THD为1.83%，并且可以直观地看出电流的正弦化程度更高了。所以利用PI-RES控制方式来抑制电机电流谐波是可行的，并且也验证了设计参数的合理性。

3.3 单位因数传统控制与新型控制对比仿真

在上述PI-RES控制基础上，对比传统的单位因数控制和新型的单位因数控制。设定仿真时间为4 s，仿真的风速v和负载PL按照图11曲线进行变化。

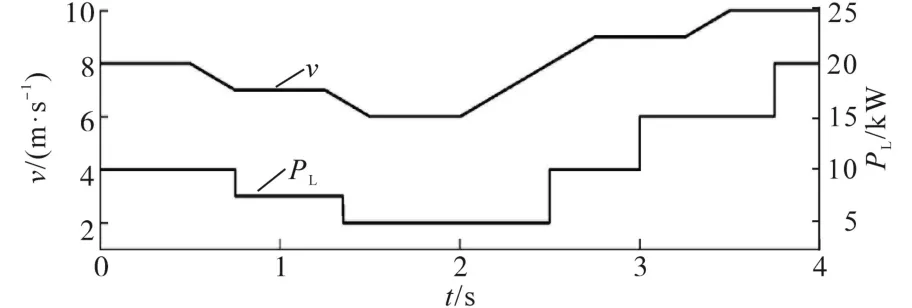
图11 风速和负载曲线Fig.11 Curves of wind speed and load

单位功率因数传统控制，也即，无功外环为零控制，通过对无功功率给定值设为零，来实现单位功率因数控制。在上述的风速和负载情况下，单位功率因数传统控制仿真结果如图12所示。在同样的风速和负载情况下，单位功率因数新型控制仿真结果如图13所示，并随机截取一段时间的usa与isa波形，观察其相位关系。

图12 单位功率因数传统控制仿真结果Fig.12 Simulation results of traditional unit power factor control

图13 新型单位功率因数控制仿真结果Fig.13 Simulation results of new unit power factor control

由图11～图13可知，在额定风速、额定负载以内的前提下，尽管风速和负载都变化，但单位功率因数传统控制和新型控制均能够在控制直流侧电压稳定在700 V的同时控制电机输出的无功功率为零，而电机输出有功功率则跟随负载的变化而变化，与风速变化无关。单独观察无功功率可知，在传统控制策略下，无功功率会随着负载变化而波动，并且在负载的有功功率越大，其波动越大，最大波动达到了4 000 var；但在新型控制策略下，即使相同的负载变化，无功功率并不波动，一直保持为零，并且相比传统控制其无功不但无波动，并且响应速度也更快。所以相比传统单位功率因数控制，从图13中的A相电压与A相电流波形可以看出，电压usa与电流isa的相位相差180°，所以在单位功率因数新型控制策略下机侧变换器实现了系统的单位功率因数运行。

3.4 i ssd给定值切换仿真

在单位功率因数新型控制策略下，isd的给定值有两种给定方式，并且从理论分析知：不同的给定值除了都能控制无功功率为零外，还能够调节输出电压。

isd给定值切换仿真参数设置如下：控制风速8 m/s，负载 10 kW，仿真时间0.7 s。在0.5 s时由较小的isd给定切换至较大的isd给定，由于0.15 s之前系统处于启动过程，所以取0.3～0.7 s的波形，仿真结果如图14所示。

图14 isd切换仿真结果Fig.14 Simulation results of isdswitching

从图14中可知：在两个isd给定值控制下均能够在稳定直流侧电压的前提下控制无功功率为零，能够实现机侧变换器单位功率因数运行；并且在较大的isd给定控制下能够使电机的输出电压降低，验证了理论分析；但在切换时，系统会有所抖动，并且较大的isd给定控制下，功率波动较大。

4 结论

本文提出了一种适用于离网型直驱永磁同步风力发电机的单位功率因数新型控制策略，依靠直接给出isd给定值的方法，使其相较于传统的单位功率因数控制，动态响应速度更快、稳定性更好、实现方法更为简单；在不同的isd控制下，该控制策略还能实现控制电机输出电压的能力，为变换器正常运行提供了条件；并且在引入PI-RES控制后，有效地解决了PI控制中电机输出电流谐波问题。仿真结果验证了理论分析的正确性及其控制策略的可行性。