计及不确定性的高比例清洁能源在微电网中的消纳

2022-02-14李晓鹏蔡文斌吕海霞

电气传动 2022年3期

李晓鹏，蔡文斌，吕海霞

（内蒙古电力经济技术研究院，内蒙古呼和浩特 010090）

近年来，随着我国实现碳达峰以及碳中和目标的提出，可再生能源（renewable energy，RE）在电网中的比例持续上升[1]。随着智能电网和微电网的发展，使得以高渗透的风能和太阳能为代表的分布式电源（distributed generation，DG）的利用更加有效。同时，风力发电和太阳能发电的间歇性给微电网带来了新的运行问题和挑战，为了保证可靠供电，当微电网出现电力供应短缺时，其他微电网元件必须能够快速、灵活地做出响应，文献[2]将这种灵活性的概念定义为：微电网能够根据可再生能源发电的短缺和过剩情况迅速修正发电量或需求量，从而总体上保持供需平衡。随着可再生能源渗透率的提高，使得电力供应的可变性和不确定性增加，维持电力供需平衡将变得更加困难，最终可能导致电力投资成本的增加来提供更高的供电可靠性。

微电网运行中的主要挑战是要满足瞬时功率平衡。储能系统（energy storage systems，ESS）作为可灵活调节出力的单元，能够对电能进行合理地转移，在时间上解耦电能的生产和消耗。让储能充分参与到系统调峰任务当中，在负荷低谷时储存电能，在负荷高峰期释放电能，减小系统峰谷差。储能的接入虽然可以在一定程度上平抑系统的功率波动，但不足以补偿高比例的风电和太阳能发电接入系统后出力的波动。需求响应（demand response，DR），旨在根据供电条件调整负荷的需求状况，从而为可再生能源发电的高渗透率的供电可能性提供支撑。已有研究表明采取有效的DR机制可以在很大程度上缩小供需之间的差距。但是，由于ESS运行需要考虑充放电损耗，而这些损耗则取决于设备的循环效率，因此DR可能会降低ESS的利用率。

同时高比例可再生能源对微电网的另一个重大挑战是如何考虑微电网中的机组组合（unit commitment，UC）决策。在可再生能源渗透率较低的情况下，UC可被视为一个确定性问题。然而，在可再生能源渗透率较高的情况下，由于风能和太阳能无法准确预测，这就导致微电网的运行中增加了一个重要的随机因素，为此传统发电机需要提供大量的备用容量，使得在接入高比例可再生能源的情况下对于减少碳排放的贡献度没有得到充分利用。

近年来，人们在解决微电网的优化调度问题上做了很多工作并取得了一定的成果。在大多数文献中，提出了两种市场策略来解决微电网的优化调度问题：一是使微电网的总运行成本最小化，包括传统发电机的运行成本和从主网获得电量的成本；二是通过与主网交换电力，使微电网的收益最大化。

文献[3]提出了一种基于微电网计及热电联产减排和发电成本的经济调度的调度模型。文献[4]提出了一个基于知识的专家系统（knowledge-based expert system，KBES），该系统为一个独立微电网提供每小时的离散调度算法。KBES通过使用ESS最大限度地减少系统甩负荷来对调度进行优化，从而降低运行成本和减少排放。文献[5]提出了一种以最小的运行成本和排放为目标，对独立运行的微电网中的分布式电源（DG）和ESS进行优化调度的优化模型。

综上所述，在负荷和可再生能源出力不确定的情况下，计及ESS和DR对微电网消纳高比例可再生能源的影响还处于研究的热点。

本文安排如下：第1节描述在UC问题中处理不确定性的主要方法，以及如何创建负荷、风能和太阳能等可再生能源出力预测误差的不确定度集。在第2节提出了微电网UC与ESS和DR的数学模型。将所建立的模型应用于微电网，并在第3节给出了仿真结果，并验证其有效性。

1 不确定因素

目前已经有很多种方法来处理负荷、风能和太阳能发电预测误差的不确定性的问题。本文采用了文献[6]和文献[7]中用于处理不确定性的方法：包含备用需求和随机优化模型。通过将这两种方法结合起来，得到最优的UC策略和更好的不确定性分析模型。备用需求是根据文献[6]中的预测误差确定的。风电出力及预测误差时域特征的研究，大多采用Markov模型与时间序列模型。前者是描述随机变量状态转移的有效方法，但其在处理短时间步长数据时存在一定的局限性。后者可以通过分析历史数据提取变量在时域上的变化特性。本文考虑的是清洁能源接入微电网的配合储能装置的中长期消纳，清洁能源在微电网中占比有限，同时储能作为备用，清洁能源随机性对电网影响能力有限，因此采用简单的基于离散误差的清洁能源随机性建模作为刻画清洁能源波动的手段。

在本文中以负荷需求、风能和太阳能发电量的预测误差百分比来表示系统运行中的不确定性。在随机优化模型中，不确定性很难考虑所有的连续状态，因此，为了简单起见，本文提取了一组有代表性的离散状态的正态离散概率分布。负荷、风电和光伏的预测误差δD，δW，δPV表示如下：

式中：e为预测中考虑状态的误差概率分布函数；ρ为对应状态出现的概率；下标D，W，PV分别为负荷、风电、光伏变量；n为该离散集中的状态数量。

通过上述的离散集来创建一个由下式给出的可能的情况（S）来表示负荷、风力和太阳能发电可能出现的偏差预测值：

通过上述提取的场景及其相应的概率，建立运行模型。

2 计及ESS和DR的UC模型

本节所建立的优化数学模型是一个多场景混合整数线性优化模型，目标函数是24 h内的预期总成本（expected total cost，ETC）最小，具体如下：

式中：λs为场景s出现的概率；K为时刻的集合；J为具备调节能力的机组集合；Cj（Pj，k，s）为机组燃料成本；SUj，k为机组的启停成本；CES为 ESS的充、放电一次的预期运行成本分别为ESS处于充电、放电的二元状态量；为限电功率；Ccurt为由于弃电导致的削减费用为功率需求的增量；CSH为需求转移的预期成本。

式（6）中，右边第一项为发电机的预期运行成本，第二项为ESS的预期运行成本，第三项为可再生能源限电的预期成本。

2.1 供需平衡约束

如下式所示总发电量（包括风能和光伏发电、ESS及DR和可再生能源电力限电）满足k期的预测需求：

式中：下标k，s为在s场景下的第k个时刻的变量；为系统总需求发生后k时刻产生的功率需求量，该需求可以大于或小于原需求量为在不考虑需求响应时的功率需求量分别为功率需求增加量和减少量。

假设负荷转移的决策由微电网运营商决定和控制，而不是由用户决定和控制。同时假设微电网运营商有关于其现有电气设备的信息系统，并可以使需求推迟到其他时间产生。关于延迟部分需求侧管理的更多详细介绍请见文献[4]和文献[8]。为了不将用户的活动转移到次日，用电需求变化必须在24 h内平衡如下式：

同时，通过下式可以得到从一个小时到另一个小时的最大转移需求量：

式中：Bup，Bdown分别为需求变化量的上、下限。

2.2 热备用约束

该约束确保所有参与备用的发电机和ESS的净可用容量满足k时间段的微电网旋转备用要求，其中还包括为减轻负荷、风能和太阳能预测的不确定性影响而增加的额外备用。

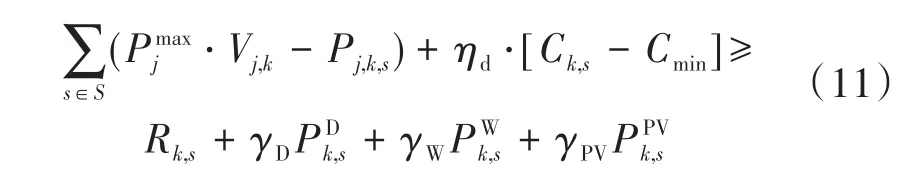
此外，每台可控发电机都有自己的运行约束条件，如升压/降压、最小上/下时间、发电输出限制、逻辑和初始约束等[9]。

2.3 储能系统约束

以下公式代表了储能系统的运行约束[10]。

2）放电和充电动态特性如下：

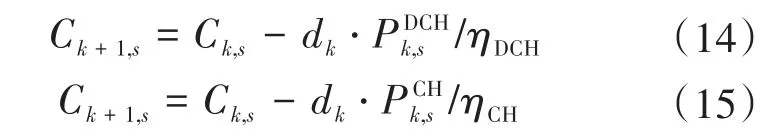
式中：Ck，s为当前储能装置的容量；ηCH，ηDCH分别为储能装置的充、放电效率；dk为当前场景的持续时间。

3）ESS运行端点和储能极限如下：

式中：Cmin，Cmax分别为储能装置最小、最大容量；C0，s为储能装置当前时刻的容量；Cst，CE分别为储能装置的初始容量和追踪容量。

4）充放电协调约束如下：

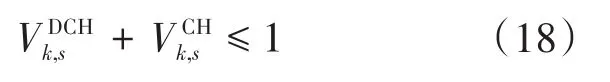
2.4 弃风弃光约束

当可再生能源发生出力过剩时，为了确保系统安全，就会采用该约束条件。通过以下3式确保当可再生能源发电量超过微电网负荷时，至少有一个有足够容量的可控机组可以提供所需的旋转备用：

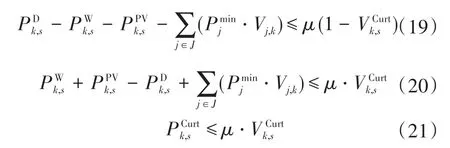
3 算例分析及仿真验证

本文采用基准微电网[11]，该微电网由12台可控DG、一台风电机组、一套光伏系统以及一套ESS组成。可控DG、风电机组和光伏系统的装机容量分别为2 040 kW，560 kW和1 440 kW。平均每小时风速曲线、风电机组参数光伏的辐照度形状的详细情况参数可参见文献[12]。可再生能源渗透率定义为可再生能源总装机容量占系统总装机容量的百分比。

微电网的24 h负荷曲线，包括商业、住宅和工业负荷如图1所示。假设微电网运营商拥有ESS的所有权和运营权。根据文献[13]假设每天有两个运行周期，电动车系统的平均运行成本估计为4.32元/（kW·h），考虑到每天两个运行周期，假设1 200元/（kW·h）的投资成本，按8%的年收益率计算，并且寿命为3 000个周期。对于ESS，当为150 kW，Cmax为900 kW·h时，Cst和CE为0.5（标幺值），而充电和放电效率为85%。

图1 所研究网络的负荷曲线Fig.1 Load curve of the study case network

为了表示不确定性，考虑了负荷、风能和太阳能预测误差的五种状态的正态离散概率分布，如表1所示，总共产生了125种场景。旋转备用约束的预测误差系数由文献[5]给出，具体如下：γD=0.03，γW=0.13，γPV=0.09。

表1 负荷、风电和太阳能的预测误差的概率分布（e，%）Tab.1 Probability distribution of prediction error of load，wind and solar energy（e，%）

假设三分之一的负荷是临界的。每小时的旋转备用需求被认为是一小时临界负荷的10%。由于负荷曲线包括工业、商业和住宅负荷，可转移需求被假定为总需求的15%。客户的负荷转移成本假定为14元/（kW·h），由于其对用户的舒适度的影响很大，所以选择了很高的负荷转移成本。

本研究考虑了可再生能源渗透程度不同的4个场景。场景1忽略了ESS和DR，以便关注不同水平的高可再生能源接入的影响；场景2只考虑了DR，而场景3只考虑了ESS，最后将两者结合起来作为场景4。

对上述4种场景进行仿真对比，每个场景和不同的可再生能源渗透水平的微电网的ETC如图2所示。图3显示了在不同的可再生能源渗透率水平下，每个场景的预期缩减能量。值得注意的是，在场景1中，当超过40%的可再生能源渗透率水平时，就需要减少可再生能源的发电量。相反，计及DR（场景2）和ESS（场景3）结合的微电网（场景4），可以将可再生能源渗透率提高到50%，而不增加预期的运行成本或造成大量的弃风弃光。

图2 不同可再生能源渗透率的ETC比较Fig.2 Comparison of ETC under different RE penetration levels

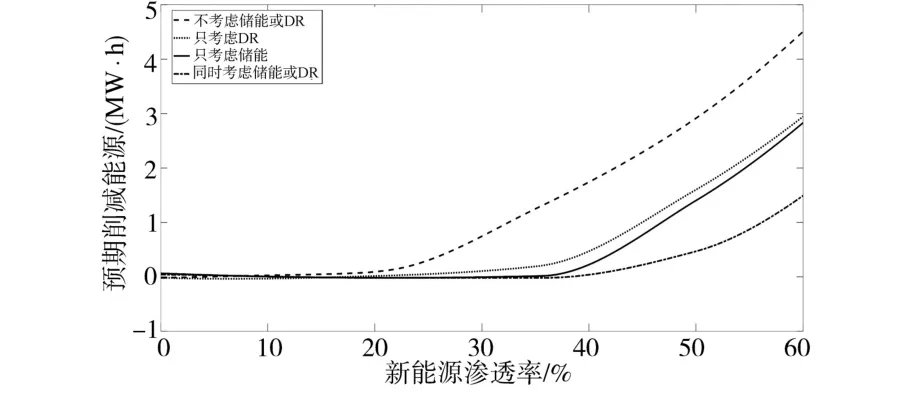
图3 不同可再生能源渗透率的预期缩减能量比较Fig.3 Comparison of expected curtailed energy under different RE penetration levels

表2、表3分别为所提出的场景研究中，在50%和60%的可再生能源渗透率水平下，微电网运行的预期成本。

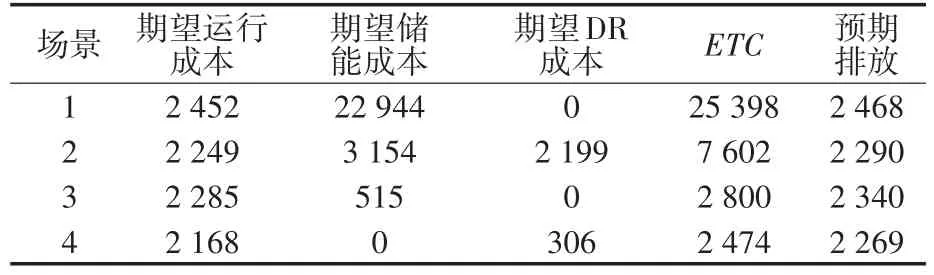
表2 50%可再生能源渗透率水平下的成本成分和排放量（美元）Tab.2 Cost components and emissions under 50%RE penetration levels（U.S.dollar）

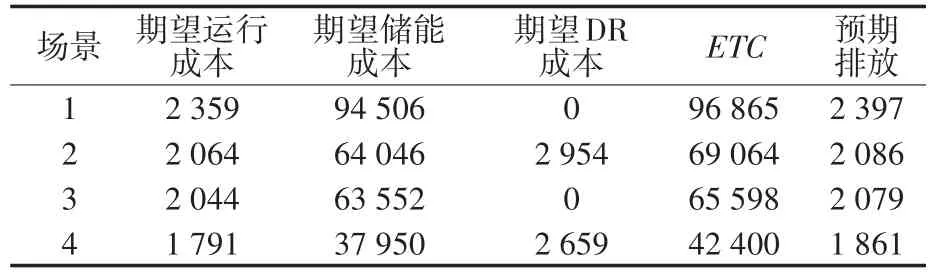
表3 60%可再生能源渗透率水平下的成本成分和排放量（美元）Tab.3 Cost components and emissions under 60%RE penetration levels（U.S.dollar）

由表2、表3可知，在场景1中，当可再生能源的发电量在某一小时k时刻超过微电网负荷时，多余的可再生能源出力在该小时内只能限电。此外，为了保证至少调度一台容量足够的可控DG机组来满足旋转备用的要求，还要对可再生电力进行一定的限电处理。在场景2中，采用DR改变微电网负荷曲线，使其尽可能地接近可再生能源功率曲线，从而使可再生能源的效益最大化，如微电网的ETC和可再生能源弃风弃光最小化。在场景3中，ESS被设置为在可再生能源发电量高的时期储存能量，在可再生能源发电量低的时期释放能量，从而减少弃风弃光，而协调ESS和DR（场景4）则有助于进一步减少可再生能源的预期限电。

通过图2可以观察到，场景1的ETC最高，原因是预期的可再生能源限电成本，表明在偏远或孤立的微电网中，如果没有ESS或DR，就不适宜接入高渗透率的可再生能源。因此，为了提高微电网的灵活性，必须将ESS和DR结合起来，从而在不发生弃风弃光的同时将可再生能源的渗透率提高到一个更高的水平。如表2、表3所示，采用这种机组组合策略也有助于进一步减少预期的微电网日排放量。