LLC谐振变换器的滑模混合控制方法
2022-02-14殷帆李先允王书征卢乙
殷帆,李先允,王书征,卢乙
(南京工程学院电力工程学院,江苏 南京 211167)
近年来,LLC凭借其可以实现一次侧开关管零电压开通(zero voltage switch,ZVS)和二次侧开关管零电流关断(zero current switch,ZCS)的特性,在直流充电桩、太阳能发电系统和电力电子变压器等场合得到越来越多的应用[1-3]。
LLC最初多采用变频控制,由于变频模式下,LLC频率变化范围不宜过大,因此在很大程度上限制了LLC的电压增益调节范围。在输入电压范围较宽的场合下,如果增益超出了变频模式的可调范围,则输出电压将不能得到很好的控制[4]。为此,许多学者提出了解决方案。文献[5]提出一种拓扑变换型LLC-C直流变换器,将两种简单谐振结构相结合,利用辅助开关管控制变换器的等效电路结构,可以获得较宽的电压增益范围,但这种方法增加了变换器的体积,且加大了参数设计难度。文献[6]提出一种新型的变结构控制方式,将全桥/半桥以及变谐振腔结构的方法相结合,在较窄的频率范围内实现宽增益变换,但该电路最多有四种工作模式,大大增加控制难度。文献[7]提出定频变母线电压和移相混合控制策略,通过增大变压器副边开关管零电流关断范围,提高变换器的工作效率和功率密度。这种控制方法可以让LLC工作在最高效率,但动态响应速度较慢。文献[8]提出一种简化最优轨迹控制,控制效果较好,但这种方法需要根据LLC的时域方程画出LLC移相模式下的状态轨迹,再根据状态轨迹进行控制器的设计,设计过程较为复杂。
综合考虑上述因素,本文提出一种基于滑模控制的变频移相混合控制策略。在变频模式下实现升压,在移相模式下实现降压。本文通过分析全桥LLC在变频和移相模式下的工作原理与数学模型,提供了详细的变频移相控制器设计步骤。该控制方法的优点是:能够很好地适应输入电压或输出电压范围较宽的场合,输出电压稳定,动态响应好,稳态误差小,鲁棒性强。
1 LLC谐振变换器工作原理
全桥LLC谐振变换器拓扑如图1所示。
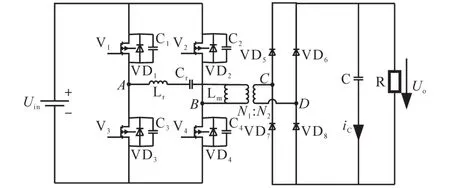
图1 全桥LLC谐振变换器拓扑Fig.1 Topology of full-bridge LLC resonant converter
图1中,Uin为直流电源电压;Uo为输出电压;V1~V4为功率开关管;VD1~VD4为 MOS 管的寄生二极管;Lr为谐振电感;Cr为谐振电容;Lm为励磁电感;VD5~VD8为副边整流二极管;C为输出电容;R为负载电阻。
在变频模式控制下,开关频率fs的范围可以分为fm<fs<fr,fs=fr,fs>fr三种模式[9-11]。其中

变频模式下,开关管V1,V4控制信号相同;V2,V3控制信号相同;V1,V4与V2,V3的驱动信号互补,各占0.5的占空比。其主要工作波形如图2所示。
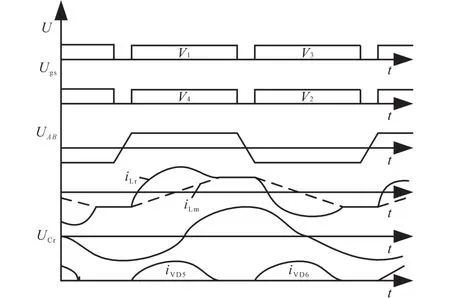
图2 变频模式工作波形Fig.2 Working waveforms of frequency conversion mode
移相模式下,LLC开关频率固定,上下桥臂控制信号互补,V1与V4的控制信号错开一个移相角[12]。图3为移相模式下变换器的主要波形。

图3 移相模式工作波形Fig.3 Working waveforms of phase shift mode
2 LLC变换器的基本特性
由第1节的分析可知,LLC变换器有变频和移相两种工作模式,本节将采用基波分析法,分别建立LLC变换器在变频模式和移相模式下的数学模型,并分析其基本特性。
2.1 变频模式基本特性
状态空间平均法等传统的建模方法在脉宽调制变换器中得到了广泛的应用,但这些方法不适用于LLC谐振变换器,基波近似法在LLC的设计中得到了广泛的应用[13]。
图4为LLC谐振变换器的基波等效电路。其中UAB为谐振腔的输入电压,变频模式下,UAB为方波,对其进行傅里叶分解并保留基波分量。

图4 LLC谐振变换器的基波等效电路Fig.4 Fundamental equivalent circuit of LLC resonant converter
基波分析法在许多文献中均有详细推导过程,在此不再赘述,直接根据图4给出基波分析法下的输出电压增益Mf表达式:

式中:Req为等效电阻;ωs为基波角频率。
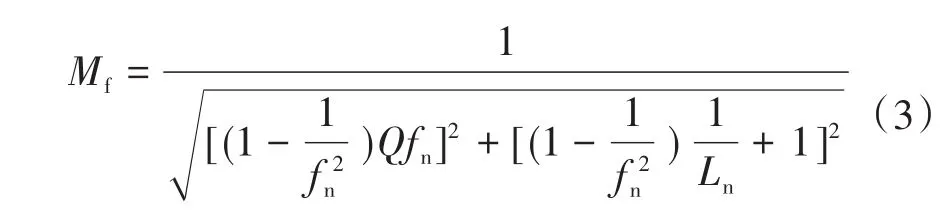
此表达式即为变频模式下LLC谐振变换器的输出电压增益表达式。
在Mathcad中得出变频模式下,不同Q值(即不同负载)情况下,增益-频率关系曲线如图5所示。

图5 增益-频率关系曲线Fig.5 The curve of the relationship between gain and frequency
根据图5可以看出,不论负载情况如何,LLC谐振变换器在谐振频率点fn处增益均为1。为了让LLC工作效率尽可能高,在变频模式下频率变化范围不宜过大[14]。当fs<fr时,Q值越小,曲线越陡,增益对频率变化就越敏感;当fs>fr时,曲线增益小于1,Q值越小,增益衰减越慢。由此可以看出,在Q值较小时,即在轻载情况下,LLC谐振变换器通过变频模式很难达到较小的增益。因此当所需增益小于1时,可以让变换器工作在移相模式。
2.2 移相模式基本特性
移相模式下,谐振腔输入电压UAB中基波含量会随移相角的增大而减小,利用基波分析法无法得出较为精确的模型。文献[15]用时域分析法列出了移相模式下各个模态下的数学模型,最后用数学分析软件绘出移相角与增益之间的关系,这种方法较为繁琐,且依然无法得出移相模式下的显式表达式。因此,本文仅采用基波分析法对移相模式下的工作特性作定性分析。
变频控制情况下,谐振腔输入电压方波的基波成分为
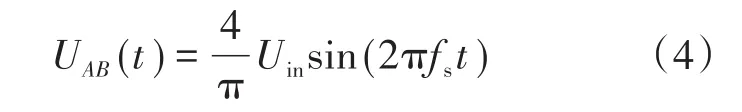
移相情况下,对输入电压作傅里叶分解,可得基波成分为

其中
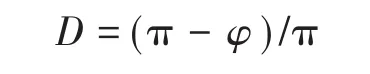
式中:D为全桥LLC谐振变换器的占空比;φ为移相角。
将式(4)、式(5)进行对比可以发现,移相模式下:

结合式(4)、式(5)、式(6),得出移相控制下的电压增益MD的表达式为
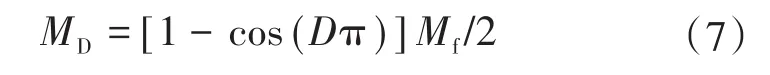
通常情况下,移相控制工作在谐振频率点fn=1处,将fn=1代入式(7),在Mathcad中绘出增益-占空比曲线图如图6所示。

图6 增益-占空比关系图Fig.6 The curve of the relationship between gain and duty cycle
由图6可以看出,随着占空比的增大,电压增益逐渐增大,当D=1时,增益为1;随着占空比的减小,电压增益逐渐减小,当D=0时增益为0。因此移相控制下,LLC变换器工作在降压模式[15]。
3 变频-移相混合控制器的设计
3.1 滑模控制器的设计
从前面的分析可以看出,LLC在变频和移相模式下的特性大相径庭。在移相模式下,变换器增益恒小于1;在变频模式下,变换器增益可在谐振点附近来回变换使得增益大于1或小于1。文献[16]采用了滑模变频控制,然而,fs需要远大于fr,才能使变换器获得较小的增益值,这在很大程度上限制了滑模控制在增益小于1情况下的电压调节能力。
为解决上述问题,可以通过判断所需的直流电压增益M=N1Uref/(N2Uin)(Uref为参考输出电压)的大小对移相和变频模式进行切换。
下面给出滑模移相-变频混合控制方法的设计过程。
首先需分别设计变频和移相模式下的控制器,过程如下。
为了尽量减少控制器需要设计的参数,滑模面选取如下式所示:

式中:k1,k2为待选取的滑模系数;e1,e2为误差变量。e1,e2定义如下:

引入控制变量u1,u2,将占空比选取函数与频率选取函数统一成矩阵形式:
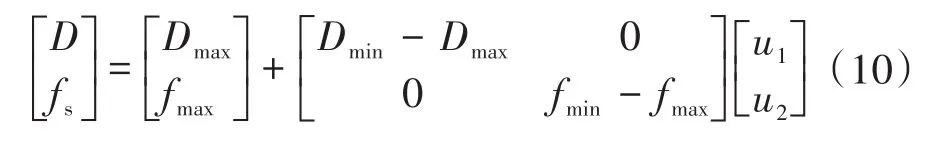
式中:Dmax为移相模式下的最大占空比;Dmin为最小占空比;fmin为变频模式下的最小开关频率;fmax为最大开关频率。
根据滑模面的大小在0和1之间的切换,设计控制变量u1,u2如下:

在实际系统中,常采用滞回比较器来保证滑模控制的可行性,因此引入滞回系数δ1,δ2,则控制变量u1,u2修改为

滑模移相以及滑模变频控制框图分别如图7a、图7b所示。
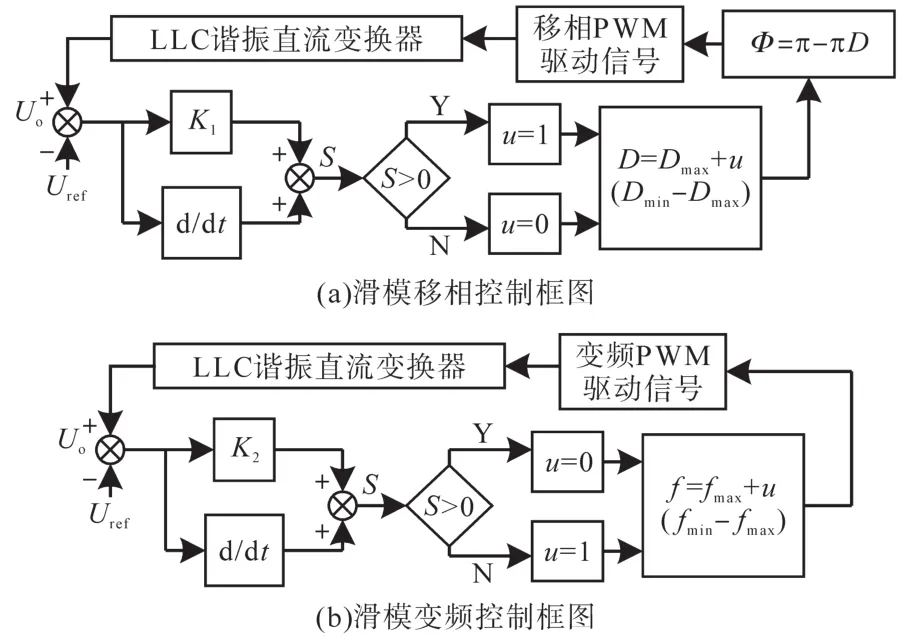
图7 滑模控制框图Fig.7 Block diagram of sliding mode control
3.2 滑模控制器稳定性分析
定义滑模变频控制与滑模移相控制下的李亚普诺夫能量函数:
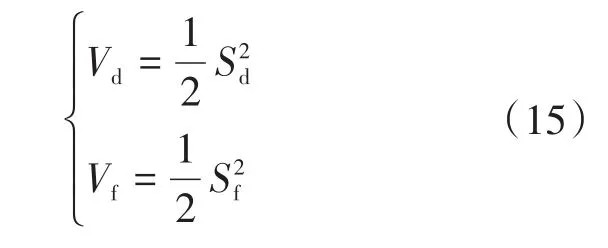
对等式两边进行求导,可得:

若系统能满足:
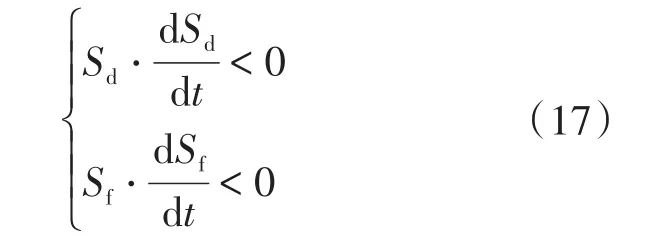
则滑模面可达且系统稳定。
移相模式下,当Sd>0时,u1=1,此时占空比D=Dmin,则输出电压Uo下降,e1,e2下降,因此滑模面Sd的值呈下降趋势,即 dSd/dt<0。当Sd<0 时,u1=0,占空比D=Dmax,此时输出电压Uo上升,e1,e2上升,因此滑模面Sd的值呈上升趋势,即dSd/dt>0。综上所述,滑模移相控制器满足式(17),同理可得变频模式下也满足稳定性。
3.3 控制器参数的设计
由于输入电压最大时所要求的增益最小,能满足此增益的占空比即为最小占空比,因此最大占空比Dmax取1,最小占空比Dmin可根据下式选取:

式中:Uin_max为最大输入电压;MD_min为最小占空比下的电压增益;Uo_nom为额定输出电压。
需要注意的是,式(18)中求出MD_min后可先根据式(7)求出最小占空比的值,但前面已经分析过,用基波分析法只是对移相模式进行定性分析,因此用该式求出的占空比并不是精确的最小占空比,且负载情况不同,移相模式下的增益特性也会有所不同,因此,用式(7)和式(18)求出占空比的粗略值后,需要结合仿真选取实际所需的最小占空比。
移相模式下的滑模系数k1主要影响系统的稳态误差以及调节时间。滞回系数δ1主要影响输出电压的纹波。根据仿真得出参数对输出电压的影响并绘制成曲线如图8所示。

图8 k1,δ1对控制性能的影响Fig.8 Impacts on control performance of k1,δ1
图8a为k1保持50 000不变,δ1变化对控制器性能的影响。可以看出,随着δ1的增大,电压纹波也会增大,因此可根据所要求的的纹波大小来选取δ1的值。
图8b、图8c为δ1保持500不变,k1变化对控制器性能的影响。可以看出,比例系数很小时,稳态误差很大,因此需要避免这种情况。随着k1的增大,输出电压稳态误差会变小,但为此付出的代价是调节时间会上升,因此选取参数时需要折中考虑。
变频模式下参数的选择方法与移相模式下的类似,限于篇幅,不再赘述。
3.4 变频-移相混合控制策略
变频-移相混合控制便是将这两种方式相结合,通过判断所需的直流电压增益Mref=N1Uref/(N2Uin)(Uref为参考输出电压)的大小对移相和变频模式进行切换,因此,切换点的选取至关重要。
假设切换点选为Mswitch=1处,这种情况下,如果所需的增益Mref=N1Uref/(N2Uin)=1,那么在输入电压有纹波的情况下,Mref也会在1附近上下波动,这将导致控制器在变频和移相模式之间频繁地切换,既不利于系统的稳定,也会对器件造成很大的影响。
因此,为避免在模式切换临界点处,由于输入电压纹波造成移相模式与变频模式的频繁切换,本文在切换过程中引入滞环,如下式所示:

式中:Mf_min为变频控制下所能达到的最小电压增益。
混和控制策略框图如图9所示。

图9 混合控制策略框图Fig.9 Block diagram of hybrid control strategy
至此,完成基于滑模控制的混合控制器的设计。
4 仿真与分析
为验证本文所提的基于滑模控制的全桥LLC混合控制策略的可行性,用PLECS搭建模型并进行仿真,并与传统PI控制进行对比。电路参数为:输入电压250~500 V,输出电压250 V,满载电流20 A,最大功率5 kW,谐振频率fr=153 kHz,变压器变比N1∶N2=11∶7,谐振电感Lr=12 μH,谐振电容Cr=90 nF,励磁电感Lm=51.5 μH,最大负载25 Ω。滑模混合控制器参数为:最大频率fmax=160 kHz,最小频率fmin=90 kHz,最小占空比Dmin=0.3,k1=186 633,k2=100 000,δ1=δ2=300。PI混合控制器参数为:变频模式比例系数Kfp=80,变频模式积分系数Kfi=2,移相模式比例系数Kdp=0.4,移相模式积分系数Kdi=4。
仿真过程如下:初始输入电压取最小输入电压250 V,此时电压增益为1.57,LLC谐振变换器工作在变频模式;0.01 s输入电压突变为最大输入电压500 V,此时电压增益为0.786,LLC切换为移相模式;0.012 s突然加载,负载由12.5 Ω变为25 Ω,测试混合控制下的鲁棒性。整体仿真输出电压波形如图10所示。
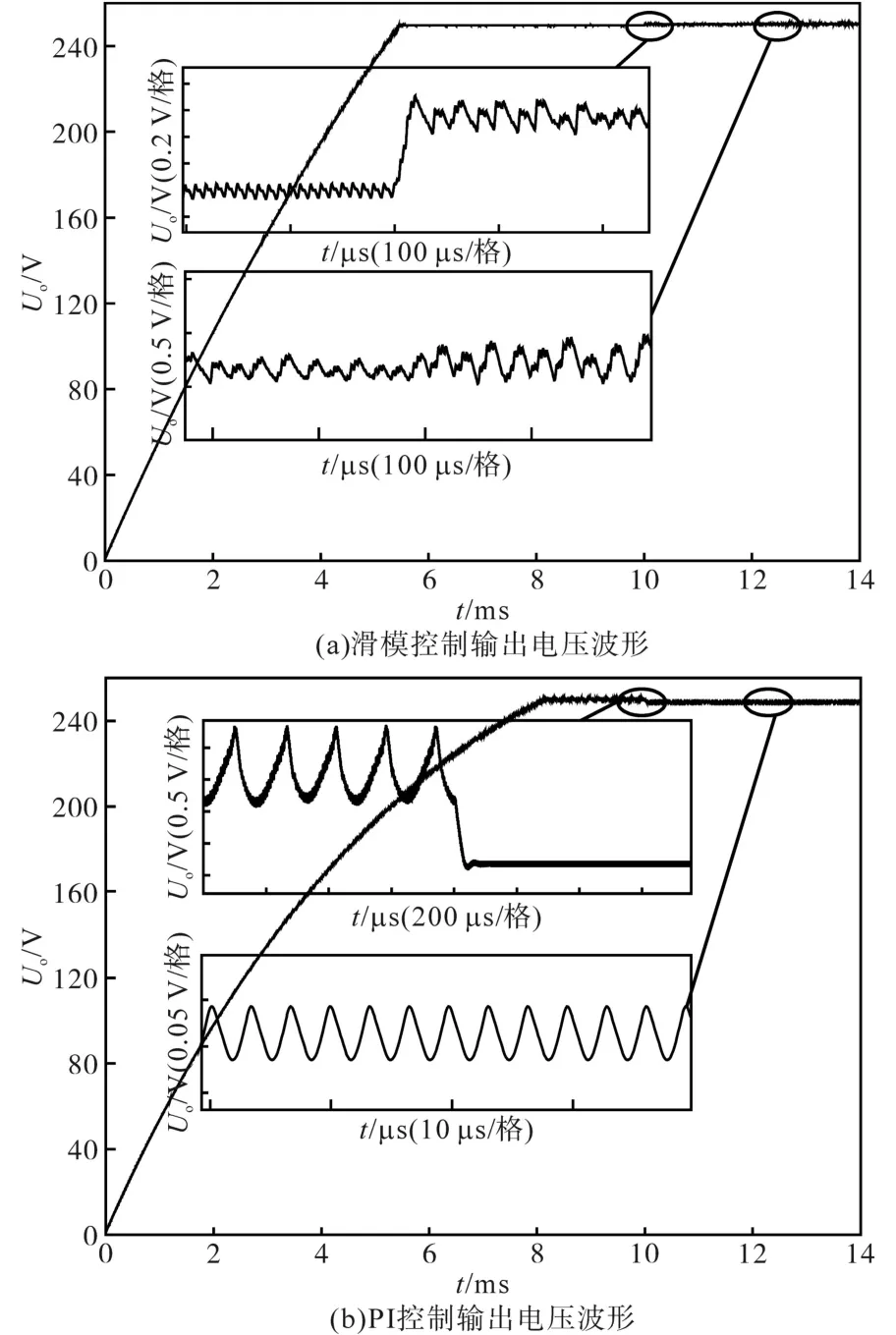
图10 滑模控制与PI控制波形对比Fig.10 Waveforms comparison between sliding mode control and PI control
由图10可以看出,PI控制下的电压上升速度较慢,上升时间比滑模控制长;0.01 s输入电压大范围突变,PI控制与滑模控制下,输出电压均仅有略微波动,然后稳定在250 V附近;0.012 s负载突变,电阻由12.5 Ω突变为25 Ω,PI控制与滑模控制的输出电压均基本稳定在250 V附近。
将PI控制与滑模控制下的仿真数据记录进行对比,对比结果如表1所示。
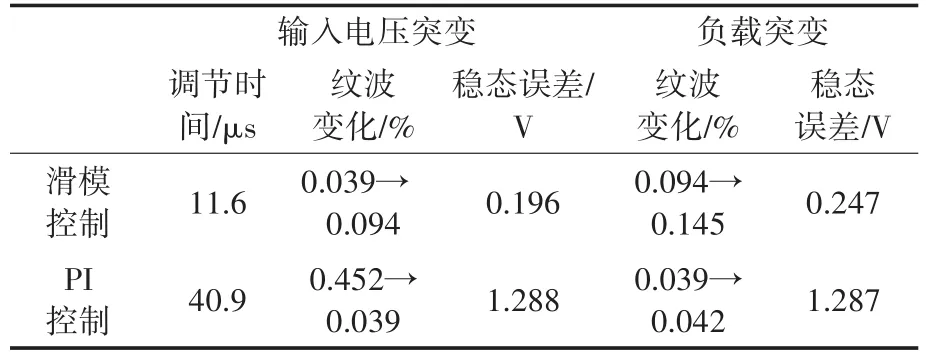
表1 PI控制与滑模控制效果对比Tab.1 Comparison between PI control and sliding mode control
由表1可以看出,输入电压由250 V突变为500 V的情况下,滑模控制的调节时间仅为PI控制的四分之一,且稳态误差也较小。这种情况下是移相滑模和移相PI在起控制作用,可见移相滑模的动态响应性能比移相PI好。负载电阻突变的情况下,滑模控制和PI控制的纹波都略微上升,总的来说滑模控制下的纹波要比PI控制下的略大,但稳态误差较小。综上所述,滑模控制的动态响应较好,稳态误差较小,鲁棒性强,纹波比PI控制略大但仍然符合工业要求。
图11为变频模式下开关管V1两端电压、电流以及二次侧二极管VD5电流波形图。图中iLr从0开始上升意味着V1开始导通,从图中可以看出,开关管电压先变为0,然后电流才由0开始增加,实现了ZVS。

图11 变频模式仿真波形Fig.11 Waveforms of frequency conversion mode
图12为移相模式下开关管V1两端电压、电流以及二次侧二极管VD5电流波形图。从图中可以看出,开关管电压先变为0,然后电流才由0开始上升,意味着开关管先变为零电压,才开始导通,实现了ZVS。
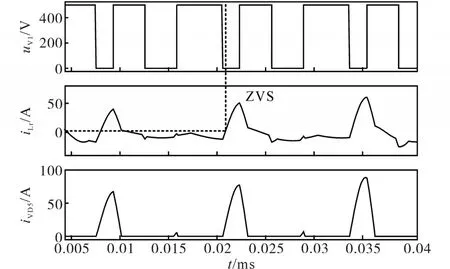
图12 移相模式仿真波形Fig.12 Waveforms of phase shift mode
5 结论
本文在对LLC谐振变换器分别在变频控制和移相控制下的原理和特性分析的基础上,提出一种基于滑模控制的LLC混合控制策略,能够较好地适应输入电压范围较宽的应用场合。仿真结果表明滑模混合控制动态响应较好,稳态误差较小,鲁棒性强,解决了LLC变换器在变频控制下电压增益范围较窄的问题。
