改进的浮体运动响应间接时域计算方法
2021-11-05扈喆张晓莹李妍李晓文
扈喆, 张晓莹, 李妍, 李晓文
(集美大学 轮机工程学院,福建 厦门 361021)
浮体在波浪中的运动响应是船舶与海洋工程领域中的常见问题,一般常基于势流理论求解此类问题。势流理论可分为频域和时域2类,其中频域势流理论经过多年发展已经成熟,且成为工程上分析浮体运动响应的常用方法。如Chen等[1]采用频域势流理论计算了柔性连接装置约束下的相邻浮体运动响应。Huang等[2]基于频域势流理论和模型试验研究了某FPSO与生活船斜对接时登乘梯的运动响应。Ghafari等[3]采用频域势流理论研究了波浪与某半潜平台和柱式FPSO的相互作用过程。王科等[4]采用基于预修正快速傅立叶变换的频域势流理论方法求解了多浮体铰接薄板结构的运动响应。
一般频域势流理论仅给出浮体在某一特定频率余弦波作用下的水动力系数和运动响应,相比之下时域势流理论可计算浮体在任意波浪激励下的运动响应。间接时域法是时域势流理论中较常用的一种方法,其将频域势流理论计算结果转化为时延函数,并据此建立浮体时域控制方程。如Choi等[5]基于间接时域法和模型试验研究了张力腿平台和半潜平台的耦合运动。Fonseca等[6]采用间接时域法研究了一系列大波作用下某FPSO的水动力载荷。李志富等[7]采用基于间接时域法的势流理论模拟了某半潜平台在畸形波作用下的运动响应和系泊缆动张力响应。纪仁玮等[8]基于间接时域法计算了振荡浮子式双浮体波浪能装置的运动响应。陈曦等[9]基于间接时域法求解浮体运动并据此建立深海浮式风机-系泊耦合分析系统。章健军[10]基于间接时域法求解浮体运动并据此建立了浮体-系泊系统运动响应异步耦合分析系统。
尽管间接时域法已经在解决实际问题中大量应用,但其在具体实施过程中存在依赖高频阻尼成分、时域附加质量确定方法模糊等缺陷。这影响了间接时域法的计算精度,进而导致间接时域法的计算结果常与频域结果存在一定差异[11-12]。研究表明这种差异很难通过缩短时间步长和提高积点个数等手段消除。针对上述问题,本文提出一种改进间接时域法,并通过数学推导证明改进间接时域法与频域法结果的一致性。以某驳船为例,对比传统间接时域法和改进间接时域法的计算结果,验证改进时域法在求解精度方面的显著提升。
1 间接时域法
1.1 传统间接时域法
有关间接时域法的理论基础已经得到充分研究讨论,这里不再叙述。Cummins[13]提出采用脉冲频谱方式建立浮体时域运动方程,即间接时域法。目前常用的间接时域法控制方程:
(1)
式中:M为浮体质量矩阵;m为时域附加质量矩阵;K(t)为时延函数;Kc为静水回复力矩阵;X(t)为浮体运动位移;F为波浪力。K(t)、m和F计算公式为[14-19]:
(2)
m=Madd(∞)
(3)
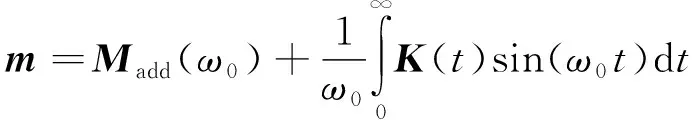
(4)

(5)
(6)
式中:Cadd为频域阻尼矩阵;Madd为频域附加质量矩阵;G为单位波幅规则波作用于浮体产生的波浪力(即RAO)。
对于式(2)和式(6)右端的积分,在t增大时被积函数迅速振荡,若不加处理,会对积分精度产生影响。目前常用的做法为采用Filon积分公式进行积分[11-12,18]。时域求解格式常采用四阶Runge-Kutta法[11-12,14,16]。
以上传统间接时域法在实际实施过程中存在以下问题:1)计算时延函数K(t)时式(2)右端积分上限无法取到无穷大;2)计算附加质量m时,若采用式(3)则实际无法给出无穷大频率对应的附加质量,若采用式(4)则右端积分上限无法取到无穷大,且ω0取不同值时得到的结果不同;3)计算g(t)时式(6)右端积分上限无法取到无穷大。
为解决积分上限无穷大的问题,最简单的做法即为直接截断,如令:
(7)
显然直接截断会导致精度损失,文献[18]指出截断频率的选取至关重要,并采用了多种函数形式对截断频率外的阻尼进行外推。
高频截断精度损失问题导致了传统间接时域法在实施过程中产生与频域法相悖的结论。例如对于任意频率为ω1的单色规则波,由频域法可知浮体的运动响应仅与该频率下的阻尼和附加质量即Cadd(ω1)和Madd(ω1)有关,原则上任何其他频率下的水动力系数均不应对ω1频率下的结果产生影响。而传统间接时域法的高频截断精度损失问题表明高频阻尼的数值将影响到ω1频率下的计算结果,与频域法的结论不符。
1.2 改进间接时域法
针对传统间接时域法的缺陷,本文提出一种改进间接时域法。改进间接时域法不采用Filon积分,对积分区间高频截断后的离散形式表达式为:
(8)
(9)
(10)
(11)
(12)
(13)
ωj=(j-1)Δω,j=1,2,…,N
(14)

显然改进间接时域法计算式(8)~(14)是间接时域法理论表达式(1)~(6)的数值实现,只是舍弃了式(1)中的时域附加质量项,改用类似时延函数K(t)的表达形式,即式(8)中左端第2项。
尽管式(8)中包含了不同频率的水动力系数,但与传统间接时域法不同,其计算实施结果与频域法完全相符,下面给出证明。
1.3 频域一致性证明
此时暂不考虑时间导数离散带来的误差,以频率为ωk的单色规则波引起的浮体运动响应为例,设η(t)=eiωkt,则:
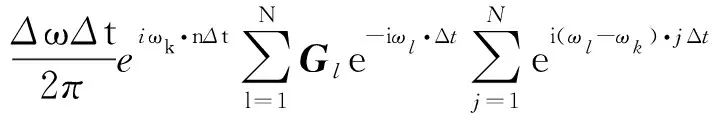
(15)
当l≠k时:
(16)
当l=k时:
(17)
故式(15)可化为:
(18)

(19)
注意到式(16)和(17),则式(19)可进一步化简为:
(20)
同理,有:
(21)
综上,在受η(t)=eiωkt波浪激励时,t=tn时系统控制方程(8)退化为:
KcX(tn)=G(ωk)η(tn)
(22)
这与频域控制方程完全一致。对于多频率成分波浪的情形,根据叠加原理,采用上面推导过程,也可以退化为频域控制方程。
2 计算结果与讨论
以某驳船为例,验证改进间接时域法的在求解精度上的优越性。驳船主要参数见表1。在驳船底部和侧面外板处划分网格,由四边形和三角形网格组成,平均网格尺寸1.5 m×1.5 m,网格数2 056,节点数2 133,湿表面模型与坐标系示意图如图1。
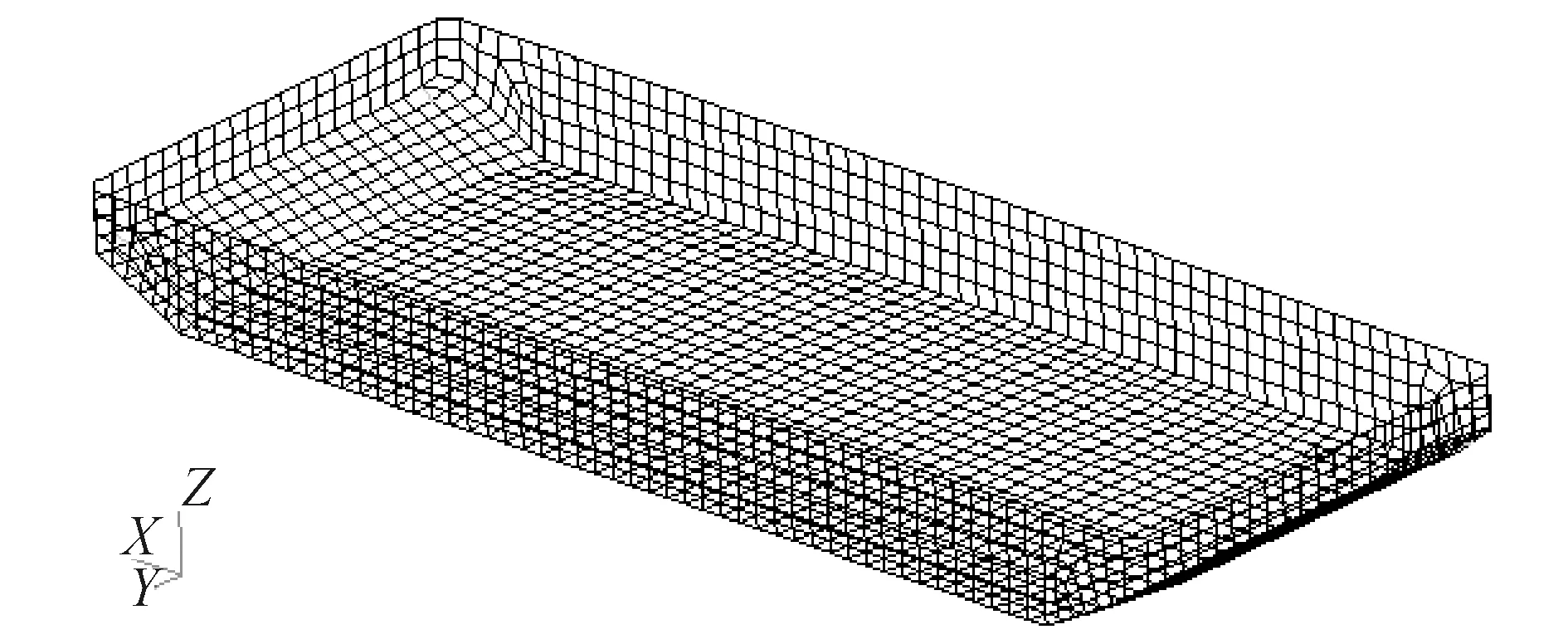
图1 驳船湿表面Fig.1 Wet surface diagram of the barge

表1 驳船主要参数表Table 1 Main parameters of the barge
首先采用频域求解器WAMIT开展频域分析计算。浪向取0°、45°和90°,频率取0.05~10 rad/s,间隔0.05 rad/s。图2以横摇为例,给出了频域分析得到的附加质量、阻尼,以及90°浪向下X方向波浪力矩RAO。
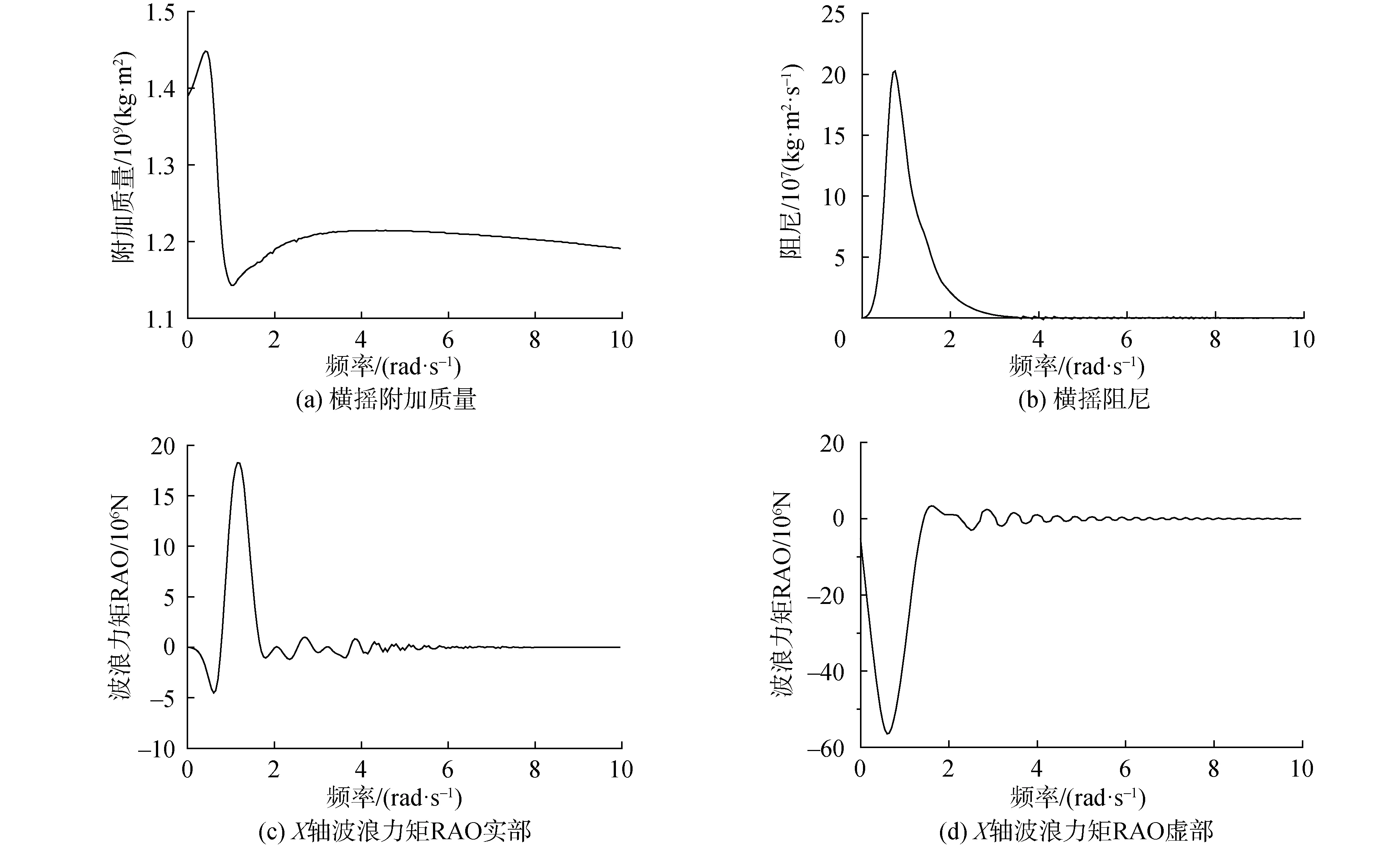
图2 90°浪向下驳船横摇水动力系数Fig.2 Roll hydrodynamic coefficient of the barge under 90° wave direction
2.1 算例一
本例选取90°浪向下,频率为0.05、0.5、1.0、2.0和6.0 rad/s的5组单位波幅波浪,采用传统间接时域法和改进间接时域法分别计算横摇运动响应,并与频域结果进行对比。图3给出了各工况下横摇角时历曲线。表2给出了传统间接时域法和改进间接时域法相对频域方法的峰值误差,即(Atmax-Afmax)/Afmax,其中Atmax为传统或改进间接时域法计算得到的横摇角振动幅值,Afmax为频域方法计算得到的横摇角振动幅值。
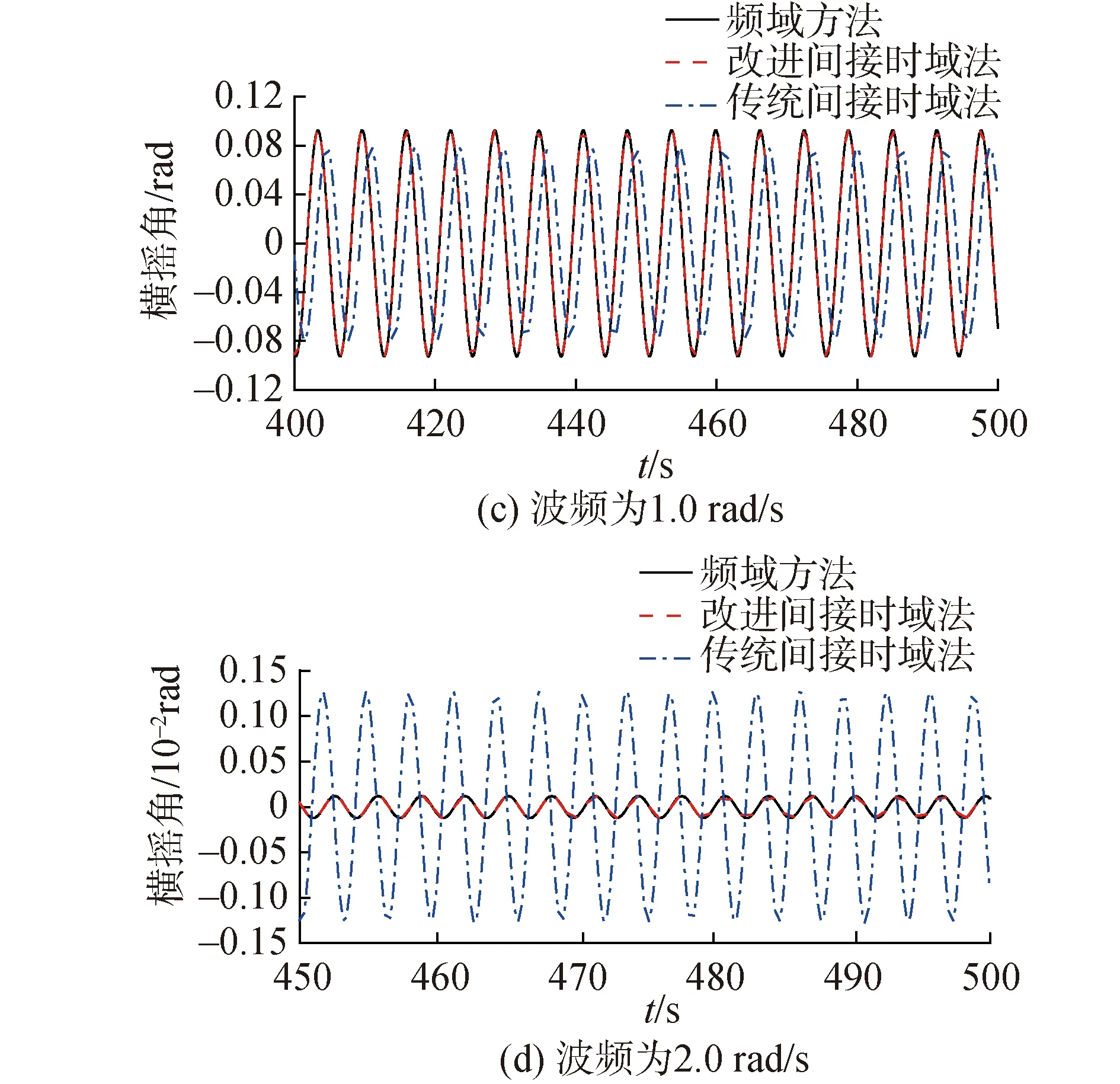
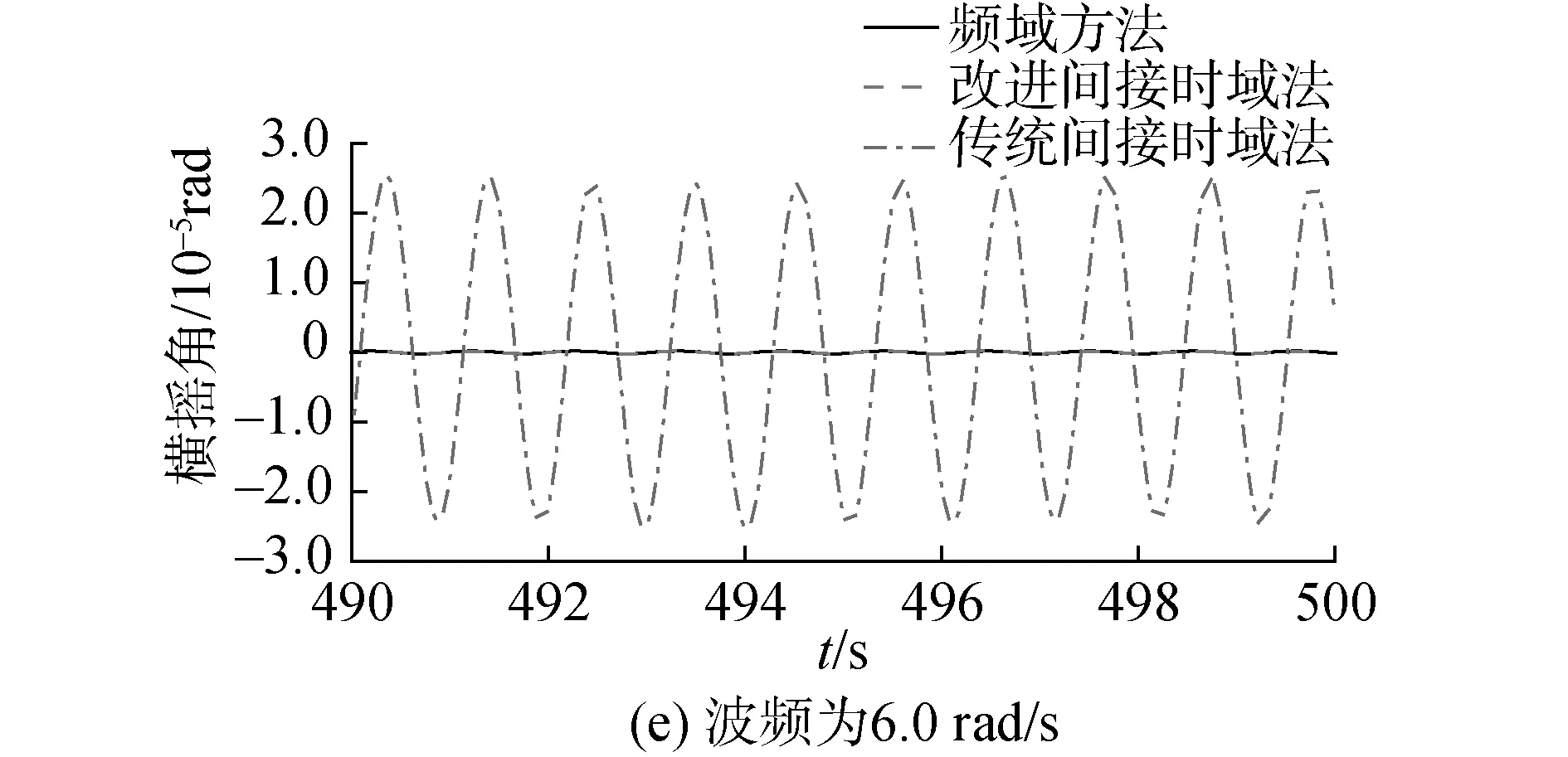
图3 90°浪向下驳船横摇角频域与时域计算结果Fig.3 Frequency domain and time domain calculation results of the barge′s roll angle under 90° wave direction

表2 横摇时历曲线峰值相对误差Table 2 Peak relative error of rolling time history curve
如图3所示,在中等波频(0.5 rad/s和1.0 rad/s)下传统间接时域法和改进间接时域法的计算结果均与频域结果吻合较好;然而对于低频(0.05 rad/s)和高频波浪(2.0 rad/s和6.0 rad/s),传统间接时域法的计算结果与频域结果存在显著差别,而改进间接时域法的计算结果仍保持与频域结果的良好吻合。从表2的误差对比中可更清楚地看到改进间接时域法的精度优势。对于本例,采用相同的时间步长,对于中等频率波浪,改进间接时域法的计算误差比传统间接时域法小2~3个量级,对于低频与高频波浪,改进间接时域法的计算误差比传统间接时域法小4~6个量级。
值得一提的是,忽略浮点数运算误差,改进间接时域法计算误差的主要来源为时域数值离散误差,虽然模拟过程中时间步长均为0.012 5 s,然而无量纲时间步长(时间步长/波浪周期)从9.95×10-5增加到1.19×10-2,这导致了表2中改进间接时域法误差自上至下依次增大。此外,尽管传统间接时域法在低频和高频波浪下的相对计算误差较大,但绝对计算误差并不大。因此传统间接时域法可用于处理一般浮体运动响应问题。相对误差较大是由于在低频和高频波浪下响应幅值本身不大,而在计算相对误差时响应幅值作为分母,放大了计算结果。
2.2 算例二
在算例一的计算中,传统和改进间接时域法的频率计算范围均为图2的横坐标范围,即0~10 rad/s。为验证改进间接时域法不受高频截断影响,在本算例中对图2中频率大于1.5 rad/s的曲线部分进行截断。基于截断后的水动力系数曲线,采用传统与改进间接时域法计算驳船横摇运动响应,并与频域结果对比。浪向取90°,波浪频率取0.05、0.5、1.0、2.0和6.0 rad/s 5组,时间步长为0.012 5 s。
图4给出了各计算工况下的横摇角时历曲线。表3给出了传统间接时域法和改进间接时域法相对频域方法的峰值误差。注意到高频截断后频率大于1.5 rad/s的水动力系数和波浪载荷均为0,即此时浮体无运动响应。因此,2.0 rad/s和6.0 rad/s频率下的频域计算结果为0,这将导致相对误差计算无意义(除数为0),故此时取绝对误差值。

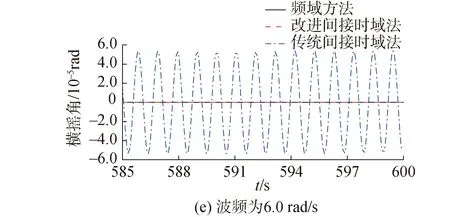
图4 90°浪向下驳船横摇角频域与时域计算结果(水动力系数高频截断)Fig.4 Frequency domain and time domain calculation results of barge′s roll angle with 90° wave direction (high frequency truncation of hydrodynamic coefficient)

表3 横摇时历曲线峰值误差Table 3 Peak error of rolling time history curve
由图4可见高频截断后改进间接时域法的计算结果仍然保持与频域结果高度吻合,相比之下,传统间接时域法的计算精度明显下降。对比表2和表3,可见无高频截断时,传统间接时域法在中等波频(0.5 rad/s和1.0 rad/s)下可以给出较满意的计算结果,而水动力系数高频截断后,同样频率下计算误差大幅度增加,表明此时传统间接时域法失效。与之相反,改进间接时域法的计算结果仍然具有高精度。特别地,当激励波频超过水动力系数对应频率上限时(2.0 rad/s和6.0 rad/s),改进间接时域法给出的结果十分接近0。
经验表明,不同截断频率对传统间接时域法的计算结果有一定影响,一般截断频率越大(即保留的RAO数据越充分),传统间接时域法的计算结果与频域结果吻合越好。但截断频率取足够大后,传统间接时域法的计算结果趋于稳定,不再改变,但与频域结果的差异始终存在。相比之下,改进间接时域法不受截断频率影响,其结果与频域结果高度吻合。
2.3 算例三
本算例验证改进间接时域法求解不规则波下浮体运动响应的准确性。波谱取双参数PM谱,根据驳船作业所在海域的实测情况,选取5种典型海况,见表4。

表4 驳船工作海域典型海况Table 4 Typical sea conditions of the barge′s working area
图5给出了各计算海况下的横摇角时历曲线。可见改进间接时域法的计算结果与频域法计算结果高度吻合,传统间接时域法计算结果与频域法计算结果在趋势上基本吻合,但曲线峰值大小存在差别,个别峰值差别较大。图6给出了各计算海况下的横摇响应谱。改进间接时域法得到的响应谱依然与频域计算结果高度吻合,传统间接时域法在海况Ⅰ~Ⅳ下得到的响应谱与相应频域结果吻合良好,但响应谱峰值偏大。对于海况Ⅴ,传统间接时域法得到的响应谱与频域结果存在较大差异,这是由于海况Ⅴ的波频成分偏大,传统间接时域法存在一定误差。



图5 90°浪向不规则波作用下驳船横摇角频域与时域计算结果Fig.5 Frequency domain and time domain calculation results of the barge′s roll angle under 90° wave direction irregular waves

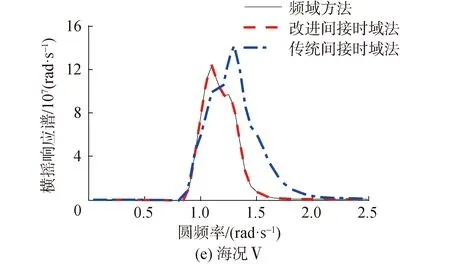
图6 90°浪向不规则波作用下驳船横摇响应谱Fig.6 Roll response spectrum of the barge under 90° wave direction irregular wave


表5 横摇响应谱整体相对误差Table 5 Relative errors of roll response spectrum
3 结论
1)改进间接时域法具有更高的计算精度,其计算结果与频域法得到的结果高度吻合。
2)传统间接时域法在计算低频和高频问题时相对误差增大,相比之下,改进间接时域法在计算低频和高频问题时不会增大误差。
3)传统间接时域法的计算结果受高频阻尼的影响。当高频阻尼截断时,低频条件下的计算结果也会受到影响,进而误差增大。相比之下,改进间接时域法不受高频截断影响,适用性更强。
