航空钛合金高效插铣加工实验与多目标优化研究
2022-02-13李益兵王辉雄庄可佳
李益兵,王辉雄,庄可佳
(武汉理工大学机电工程学院,武汉430070)
近年来,钛合金材料因其密度低、强度高、耐腐蚀性好等特点在航空发动机整体叶盘、机匣等关键部件中,钛合金被大量使用[1]。钛合金整体叶盘结构复杂、叶片为自由曲面、流道加工空间狭小,材料难切削、加工余量大,制造难度较大[2]。传统的侧铣加工中刀具主要受径向力作用,随着刀具悬伸量的增加,切削系统刚度降低,容易产生颤振,刀具磨损加剧,严重时刀具折断,工件质量下降,加工效率显著降低。而插铣过程,刀具沿主轴方向进给,刀具主要受轴向力作用,径向力相对较小,刀具悬伸量较大。结合插铣的特点,将插铣技术应用于钛合金整体叶盘制造可有效解决上述问题。
Li 提出了一种圆柱形零件的插铣方法并且建立了瞬时切削力的预测模型[3]。Altintas和Jeong 系统地研究了插铣加工的瞬时切削力模型及振动模型[4-5]。Damir 研究了刚性和柔性工件系统的时域切削力和稳定性分析[6]。岳彩旭建立了动态切削力系数的切削力机械模型,在该模型基础上研究了插铣加工的切削力和稳定性分析[7]。Zhuang 建立了考虑刀具跳动的插铣瞬时切削力解析模型和机械模型,模型的预测值与实验结果非常接近[8-9]。
除了加工机理方面的研究外,研究了切削参数对加工性能指标的影响,对切削参数进行优选,以提高加工效率、提高工件质量和减小生产成本等。任军学及其团队做了一系列钛合金插铣试验,研究了插铣参数对切削力、表面温度的影响规律,并以刀具许用挠度为约束,提出了切削参数选择的方法[10-11]。Zhuang 等基于精确的切削几何形状,建立了插铣瞬时切削力的机械模型,并以颤振稳定性为约束优化切削参数,提高了材料去除率[12]。Danis等研究了镁合金插铣过程中切削条件对表面完整性的影响,给出了切削条件以达到表面完整性和加工效率之间的平衡[13-14]。Fredj等研究了插铣钛合金过程中不同的刀具类型和切削参数对切削力的影响规律[15]。
上述研究主要集中在插铣的切削力建模与稳定性分析及实验等方面,很少应用智能优化算法对插铣过程的切削参数优化。此外,在切削参数选择中,没有涉及到多个目标同时优化问题,而是以部分目标作为约束条件进行参数选择。实际加工过程中,各目标是相互冲突和影响的,使多个目标同时达到最优的切削参数组合往往是不存在的,只能在它们中间进行协调和折中处理,尽可能使各目标达到最优。本文以航空发动机整体叶盘材料TC4 钛合金作为实验材料,选用响应曲面法设计实验,测量插铣切削力,建立切削力与切削参数之间的数学模型,分析切削参数对切削力的影响规律。以材料去除率和切削力为目标,基于带精英策略的非支配排序遗传算法(Non-dominated sorting genetic algorithm, NSGA-II)优化切削参数,以最大化材料去除率和最小化切削力。
1 实验与测量
本实验以主轴转速、切削宽度、切削步距和每齿进给量为可控切削参数,测量不同切削参数组合情况下的加工性能指标。
1.1 实验材料、刀具及设备
选用尺寸为125 mm×100 mm×40 mm 的TC4合金为实验工件材料,其各元素的质量分数见表1。

表1 TC4钛合金各元素的质量分数%
选用机床为MIKRON VCE 800W Pro立式加工中心,最大转速10000 r/min。选用山高制造的直径12 mm 两齿铣刀,刀杆型号MM12-12055.0-0008,刀片型号MM12-12008-R10-PL-MD05 F30M。在干切削条件下进行实验,插铣方式为逆铣,选用Kistler 9257B测力仪测量实验切削力。实验装置如图1 所示。

图1 实验装置
1.2 实验设计
响应曲面法(Response surface methodology,RSM)集合了数学和统计技术,能够通过较少的实验次数来节省成本和时间,将响应与因素之间的关系映射成数学模型,分析因素对响应的影响规律,获得响应最优的因素值[16]。当寻找响应的最优值时,通常需要包含曲率的模型来近似预测响应。一般情况下,采用的二阶模型形式为
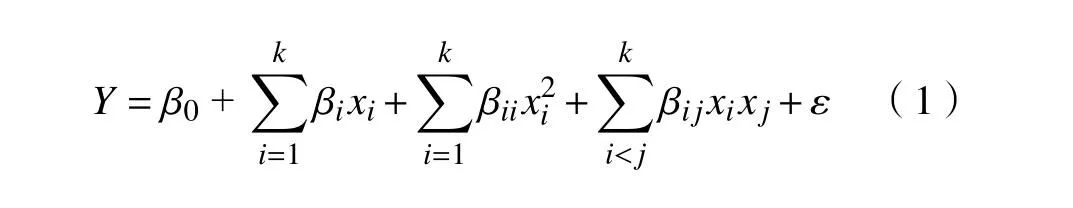
式中:Y 为预测的响应值;k 为设计变量个数;xi和xj均为设计变量;β0、βi、βii和βij分别为常数项、线性项、平方项和交互项的系数;ε 为残差。
中心复合设计(Central composite design,CCD)是RSM中使用最广泛的一种实验设计方法,它非常适用于拟合2阶模型。一般来说,CCD包括2k个因子点、2k 个轴点和nc个中心点。本实验因素为4个切削参数,轴点到中心点的距离α=2,因子点个数为16,轴点个数为8,中心点数量设置为6个,共30组实验。切削参数的编码及水平如表2所示。
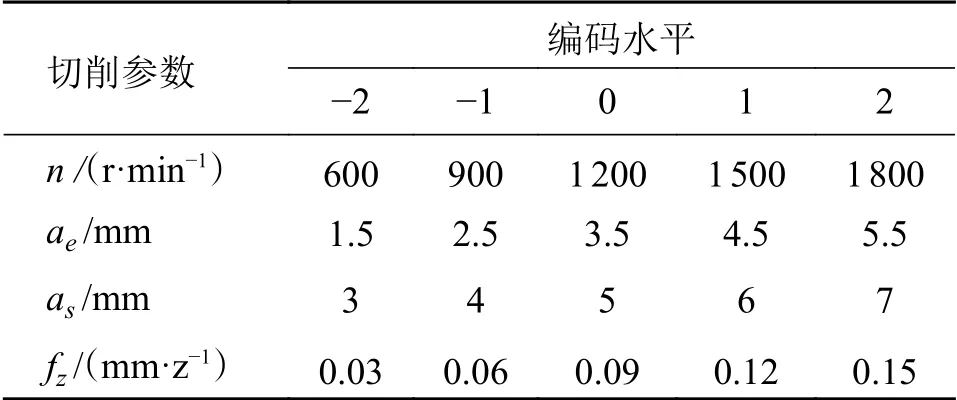
表2 切削参数的编码及水平
2 结果分析
采集的三向切削力信号局部放大图如图2所示,由图可知在插铣中轴向是主要受力方向。本实验切削力数据用最大切削合力表示,30组实验参数组合以及对应的材料去除率(Material removal rate,MRR)和最大切削力Fc结果如表3所示。

图2 切削力信号局部放大图

表3 实验数据
2.1 建立切削力模型
为了更好地预测切削力,通过实验数据建立了一个切削力2阶模型。拟合的切削力2阶模型为

该模型通过后向消除法去除了不显著项。建立模型之后,对模型进行方差分析,验证模型的可靠性。模型方差分析表如表4所示。在方差分析表中,F 和P 值用来判断模型和参数项的显著性。F 值越大,P 值越小,显著性越高。当P 值小于0.05时,表示该项在95%的置信度水平下对响应有显著影响。

表4 方差分析表
由于模型消除了一些不显著的参数项,表4显示的P 值都小于0.05。由表4可知,模型的P 值小于0.001,在95%的置信度水平下是显著的。模型的R2、调整R2和预测R2分别为99.40%、99.03%和97.84%,这些值都非常接近于1,表明建立的模型非常有效。每个参数对Fc的百分比贡献如表4最后一列所示,在4个主参数中,切削宽度ae是影响Fc最显著的参数,其次是每齿进给量fz、切削步距as和主轴转速n。
模型预测值与实验值的对比如图3所示,预测值与实验值接近。经计算,预测值与实验值的最大误差为11.89%,平均误差为2.73%,说明该切削力预测模型的准确性和可信度较好。30次实验的残差散点图如图4所示,残差随机地分布在水平轴上下,无不正常的升降趋势。残差正态性检验图如图5所示,残差几乎落在一条直线上,残差正态性检验P=0.479,大于0.05,可以认为残差是呈正态分布的。从以上分析可以得出,建立的模型是有效的、充分的和可靠的,它能够较准确地预测切削力。

图3 切削力预测值与实验值
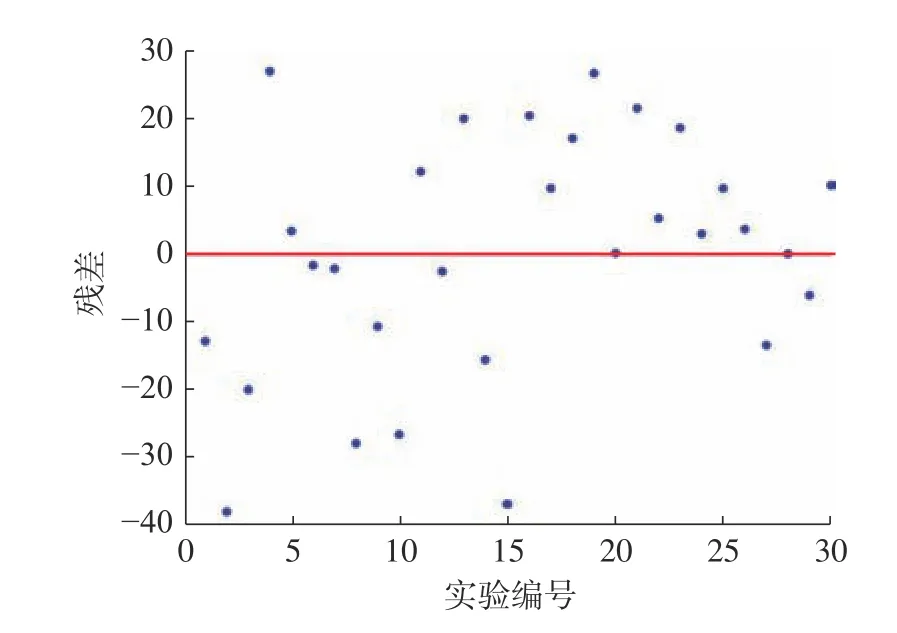
图4 残差随实验编号分布的散点图

图5 残差的正态性检验图
2.2 切削参数对切削力的影响
在建立的2阶模型基础上分析切削参数对切削力的影响,切削参数对切削力影响的曲面图如图6~图9所示。
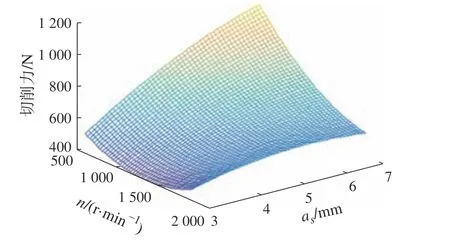
图6 n和as 对Fc 的影响
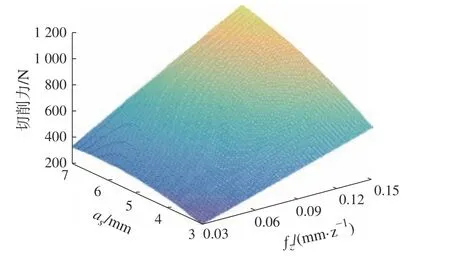
图9 as 和fz 对Fc 的影响
从图6和图7可以看出,切削力Fc随着主轴转速n的增加而减小,但是减小的幅度比较小。这是由于随着n的增加,金属的局部温度、应力和应变升高,从而导致切屑厚度减小[17]。另一方面切削温度升高,金属材料发生热软化,摩擦力和切削抗力减小。as和fz值越大,Fc随n减小的幅度越大,这是由于当ae和fz取较大的值时,切削温度越高,热软化现象越明显。
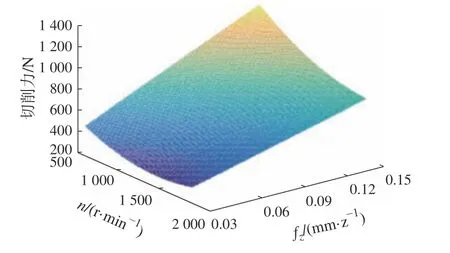
图7 n和fz 对Fc 的影响
从图6、图8和图9可以看出,Fc随着切削宽度ae和切削步距as的增加而增加,ae对Fc的影响比as大。这是由于ae和as增加,刀具单位时间材料去除量增加,铣刀直接参与切削的切削刃长度增加,铣削面积和摩擦面积增加,从而Fc增加。由于插铣加工方式的特点,材料去除量随ae增加的幅度比as大,所以ae对Fc的影响大得多。
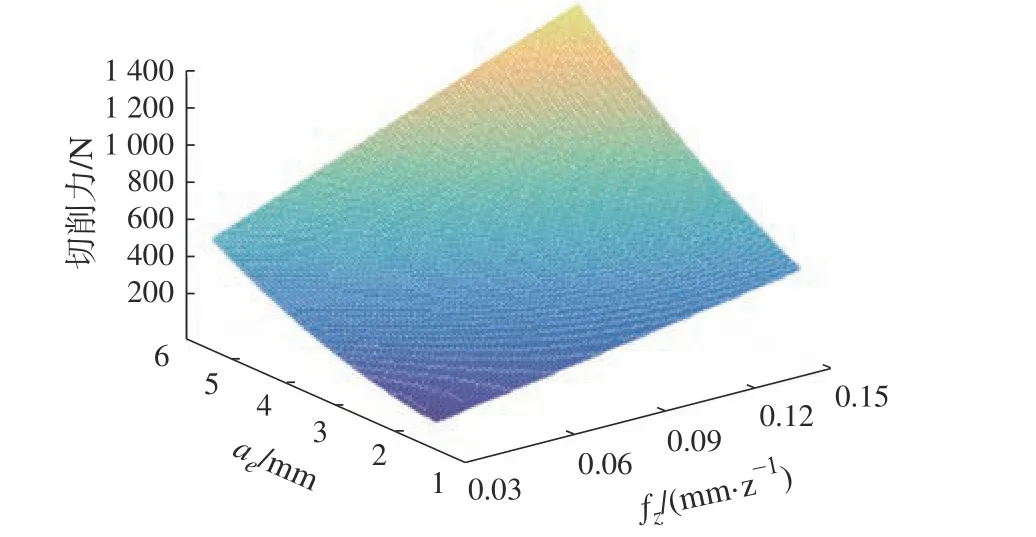
图8 ae 和fz 对Fc 的影响
从图7~图9可以看出,Fc随着每齿进给量fz的增加而增加。由于fz的增加,切削厚度增加,切削刃单位时间材料去除量增加,切屑厚度增加,所需的切削力增加。虽然fz和ae对Fc的影响几乎都是成正比关系,但由于进给量的增加会减小切削层的变形,所以fz对Fc的影响比ae小。
从以上分析可以得出,切削力随主轴转速的增加而减小,随切削宽度、切削步距和每齿进给量的增加而增加。变化的幅度从大到小依次为切削宽度、每齿进给量、切削步距和主轴转速,这同时表示切削参数对切削力的影响程度,与2.1节的分析结果一致。加工时要得到较小的切削力,可以选择较大的主轴转速,较小的切削宽度、切削步距和每齿进给量。
2.3 多目标优化
从第2.2节的分析可以得出,较高的主轴转速、小切削宽度、小切削步距和小每齿进给量可以获得较小的切削力。但是在小切削宽度、小切削步距和小每齿进给量的条件下,加工效率无法得到提高,无法体现插铣加工的优势。材料去除率MRR指的是单位时间内的材料去除量,可以用来表示加工效率。根据文献[12]插铣加工的材料去除率MRR可表示为
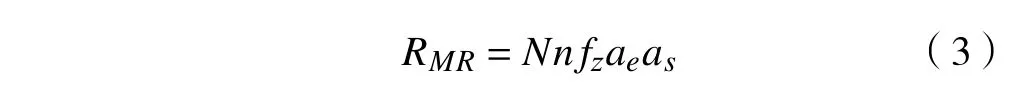
式中:N 为刀具齿数;n为主轴转速;fz为每齿进给量;ae为切削宽度;as为切削步距。
不合理的切削参数容易产生较大的切削力和较低的加工效率,因此以小Fc和高MRR 为目标,选择合理的切削参数是有必要的。材料去除率MRR和切削力Fc相互冲突,优化一个目标会造成另一个目标变差。因此本节以MRR 和Fc为目标,采用NSGAII算法进行多目标参数优化,以最大化MRR 和最小化Fc。
本次多目标优化可规划如下:
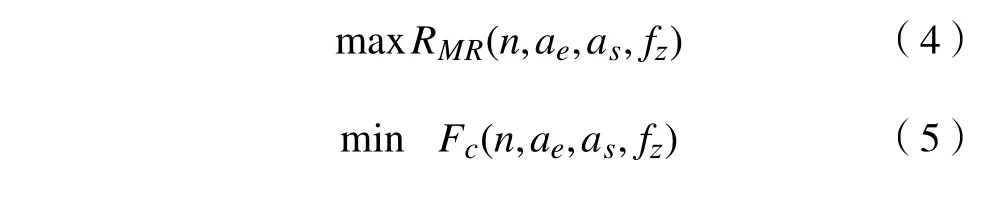

式中:Fc和MRR的模型分别采用式(2)和式(3)的数学模型。
本文多目标优化方法主要分成两个阶段:第一阶段建立一个切削力经验模型,主要用来准确地预测切削力Fc;第二阶段为多目标优化过程,以第一阶段建立的预测模型为适应度函数,在MATLAB环境下通过NSGA-II算法找出Pareto最优解集。
NSGA-II算法种群规模200,进化代数为200 代。获得的Pareto最优解集如图10所示,X 轴和Y 轴分别表示MRR和Fc。由图10可知,在Pareto前沿上,当一个响应改变时,另一个响应也会发生变化。很明显,当MRR增加时,相应的Fc也会增加。表5列出了Pareto最优解集中的20个解,以及每个解对应的切削参数值。值得说明的是,由于采用的是启发式算法,每一次运行的结果都会略有不同。可以根据需求,选择适合的切削参数组合。比如,当规定切削力不能超过1000 N 时,材料去除率能达到的最大值为15800 mm3/min。
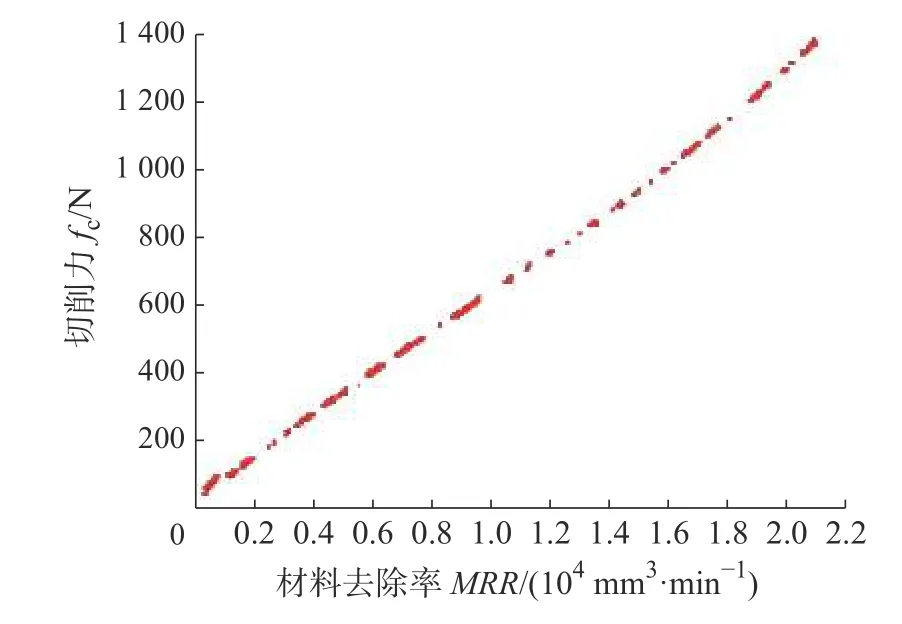
图10 Pareto最优前沿
为了验证多目标优化的效果,将实验中心点水平的参数组合(n = 1200 r/min、ae= 3.5 mm、as= 5 mm、fz=0.09 mm/z)作为实验初始参数组合与部分Pareto最优解对比,结果如表6所示,其中实验中心点的切削力为6个中心点的切削力平均值。从表6可知,当取表5中的第5组实验参数时,预测的MRR为9221.248 mm3/min ,Fc=602.86 N,MRR增加了143.95%,而Fc减小了1.22%。当取表5中的第6组实验参数时,预测的MRR为3836.536 mm3/min,Fc为279.059 N,MRR增加了1.50%,而Fc减小了54.28%。当取表5中的第11组实验参数时,预测的MRR为6874.44 mm3/min,Fc=465.791 N,MRR增加了81.19%,而Fc减小了23.68%。因此,与实验中心点对比,根据优化的切削参数,可以大幅度增加MRR而Fc几乎不变化,可以保持MRR不变而大幅度减小Fc,也可以得到两个目标都优化的结果。
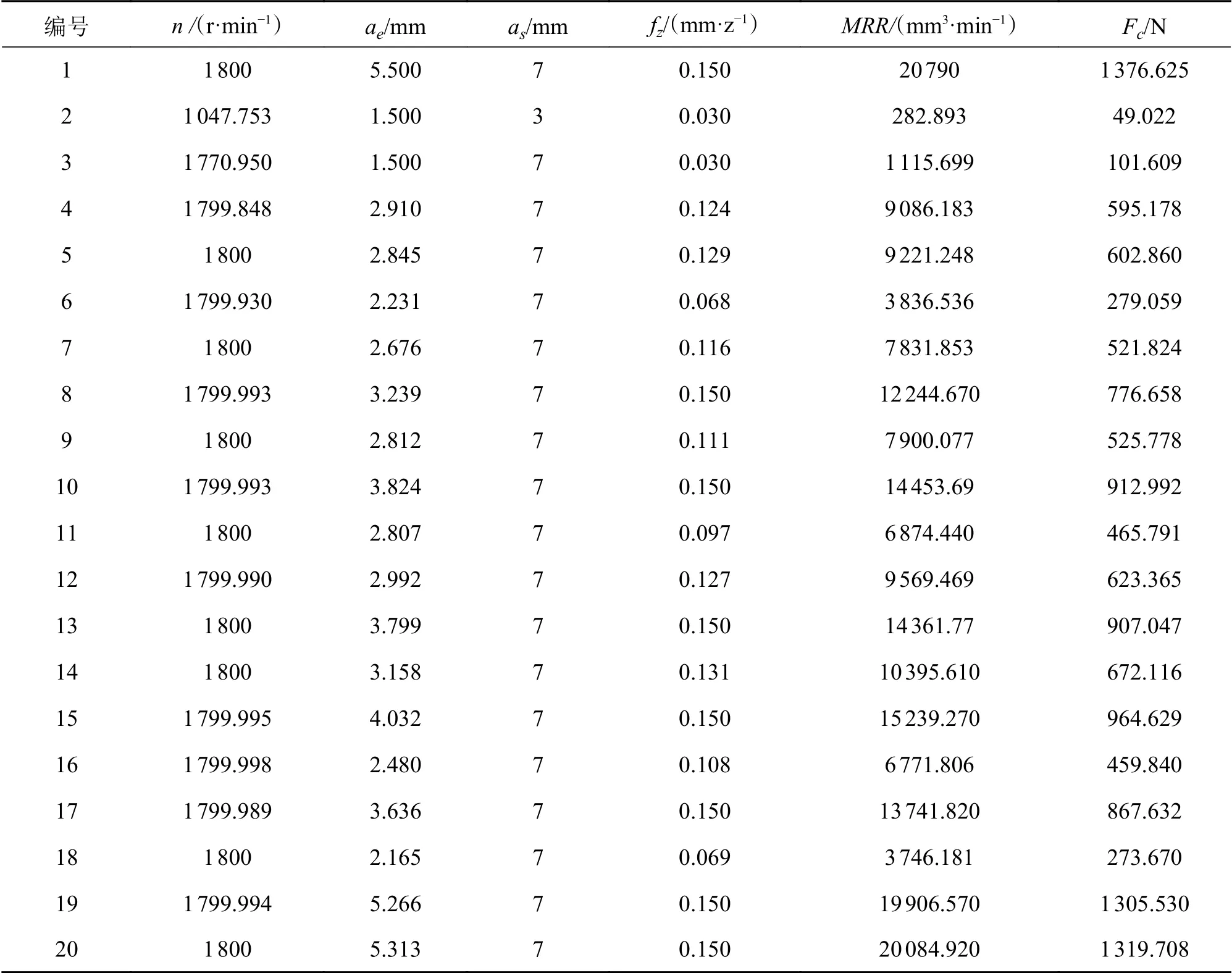
表5 预测的20个Pareto最优解

表6 优化与实验中心点对比结果
3 结论
1)应用响应曲面法RSM建立的钛合金最大插铣切削力模型是有效的和可靠的,模型的预测值与实验值接近,最大误差低于12%,可以有效预测插铣过程切削力。
2)钛合金插铣切削力随着主轴速度n的增加而减小,随着切削宽度ae、切削步距as和每齿进给量fz的增加而增加。对模型进行方差分析得出:切削参数对插铣切削力的影响程度从大到小依次是切削宽度ae、每齿进给量fz、切削步距as和主轴速度n。
3)以最大化材料去除率和最小化切削力为目标,利用NSGA-II算法进行多目标优化,与实验初始参数对比,优化的结果能够显著提高材料去除率和减小切削力。
