含腐蚀缺陷的非粘结柔性管骨架层承载分析*
2022-02-13鲁中歧崔俊国肖文生王魁涛
鲁中歧 崔俊国 肖文生 王魁涛 张 俊
(1.中国石油大学(华东)机电工程学院 2.中海油研究总院有限责任公司)
0 引 言
腐蚀缺陷严重影响了油气管道的承载能力,进而影响其运载寿命。目前,国内外学者针对腐蚀缺陷形貌尺寸对传统刚性管道承载能力影响关系进行了深入研究,其中部分专家借助数值分析软件建立了管道有限元模型,对矩形和球形等不同形状的单个腐蚀缺陷进行了模拟,分析了腐蚀形貌对管道失效压力的影响[1];不少学者也对腐蚀缺陷的长度、宽度及径向深度对管道承载能力的影响规律进行了研究,得出了腐蚀缺陷深度对管道失效压力影响最大、缺陷长度次之、缺陷宽度影响最小的结论[2-4]。还有一些研究人员对存在轴向、环向及交叠等情况的组合腐蚀缺陷对管道等效应力的影响规律进行了探讨,得出结论如下:轴向及环向存在多个腐蚀坑时,存在一个临界距离,大于该临界距离时,两腐蚀缺陷不会相互影响;对于交叠分布缺陷,小缺陷对等效应力的影响不可忽略[5-7]。
以上研究都是针对于传统刚性管,而柔性管道相比刚性管道具有更大的优势,逐步得到广泛应用。柔性管最内层骨架层与运输介质直接接触,不可避免地会有腐蚀发生,进而影响管道的承压能力,导致管道失效。然而针对该腐蚀缺陷对于管道承载能力影响规律的研究还比较少。国内外相关专家通过数值分析的方法,探讨了材料非线性、初始椭圆度、相邻节之间的接触方式及螺旋缠绕角度等因素对均匀荷载或对径向压力下的骨架层失效压力的影响,得出了材料非线性对骨架层的抗压溃能力影响最大,初始椭圆度及接触方式影响次之,螺旋缠绕角度影响最小的结论[8-13]。
上述针对柔性管骨架层的研究都在无腐蚀缺陷情况下进行,有关腐蚀缺陷对非粘结柔性管骨架层的承压能力研究较少。为此,笔者结合已有研究成果,借用ANSYS Workbench软件建立了柔性管骨架层的有限元模型,研究了腐蚀形貌尺寸及腐蚀形式对骨架层失效压力的影响规律,并借助分析结果对骨架层的腐蚀状态进行了划分。研究结果可为柔性管腐蚀程度评价提供借鉴。
1 理论模型研究
圆环在均匀外压载荷下的屈曲载荷值[8]可结合铁木辛柯弹性稳定理论中圆环挠曲线微分方程推导,具体如下:
(1)
(2)
式中:q为圆环均匀外压下的屈曲载荷,MPa;I为圆环矩形截面惯性矩,m3;b为矩形截面长,m;t为矩形截面宽,m;R为圆环半径,m;E为材料弹性模量,MPa。
对于传统均质圆环,截面为长方形,于是单位长度下的平面应力临界压溃值qcr为:
(3)
由于非粘结柔性管骨架层截面形状十分复杂,可依据下式计算等效厚度teq:
(4)
式中:IGmin为骨架层截面的最小主惯性矩,m4;A为截面面积,m2。
本文选取内径101.6 mm(4 in)非粘结柔性管道为研究对象,骨架层截面尺寸如图1所示[14]。
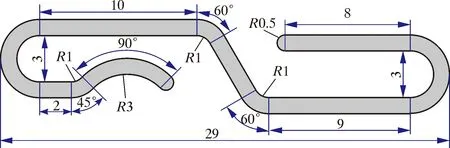
图1 骨架层截面
该骨架层截面面积A为56.210 7 mm2,最小主惯性矩IGmin为181.172 5 mm4。
将以上参数带入式(4)可求得骨架层的等效厚度teq为6.219 1 mm。圆环半径取中径[9],即有:
(5)
式中:R1为非粘结柔性管最内层半径,mm。
带入式(5)求得R为52.409 5 mm,骨架层材料为316L不锈钢,弹性模量E为206 GPa。将弹性模量E、等效厚度teq及半径R带入式(3)求得单位长度下平面应力临界压溃值为79.06 MPa。
2 有限元模型分析
2.1 模型验证
根据现有文献,骨架层的螺旋缠绕角度对均匀外压下临界压溃值影响较小,因此在研究中可以忽略不计。对骨架层承载能力影响较大的因素有材料非线性、初始椭圆度以及骨架层相邻节之间的接触方式[7]。其中材料非线性指的是材料的弹塑特性,即当应力超过材料的屈服极限时,应力与应变之间呈现一种非线性的增长关系,该因素对骨架层承载能力影响最大;骨架层在制造及安装过程中,难免会有夹持等情况出现,从而导致其形状改变,通常会呈现一种椭圆形状。规定以椭圆的长径与短径之差和两者之和的比值作为衡量其发生椭圆变形的标准,称之为椭圆度。椭圆度越大,骨架层的承载能力越小。骨架层相邻节之间的接触方式对承载能力有所影响,例如绑定接触或摩擦接触以及摩擦接触的摩擦因数等,同样会影响骨架层的承载能力。本文所研究骨架层材料为316L不锈钢,在0.2%初始椭圆度、相邻节之间为摩擦接触、摩擦因数为0.15的情况下分析其承载能力。
首先建立管道整体模型,如图2a所示。在不考虑材料非线性、初始椭圆度及节间接触的情况下,对其进行特征值屈曲分析,查看管道的压溃形式,同时分析压溃的临界载荷值,与理论值进行对比,验证理论模型的准确性。该分析中,骨架层的各节之间为绑定接触,在管道轴向两端限制轴向位移约束,同时打开弱弹簧开关,骨架层外表面施加1 MPa的均匀载荷。骨架层及特征值屈曲分析结果如图2b所示。

图2 骨架层整体有限元分析
由图2b可知,屈曲载荷系数为76.672,屈曲载荷等于屈曲载荷系数乘以施加载荷,由于施加的是单位载荷,所以屈曲载荷为76.672 MPa,即骨架层在该设定条件下的失稳值为76.672 MPa,与理论值对比如表1所示。

表1 特征值屈曲分析结果对比
由表1可知,骨架层特征值屈曲分析值与理论计算值很接近,验证了用理论模型来计算无节间摩擦、完美圆状态下弹性材料管道临界失稳值的准确性。
2.2 数值模拟分析
在工作实际中,上述理想条件比较少,仅靠理论模型不能满足要求,可借助数值模拟来进行分析。结合实际及现有理论,材料弹塑性对骨架层的承载能力影响很大,对于塑性材料,当应力超过比例极限后同样采用上述分析显然不合理。对于塑性分析有塑性极限载荷和塑性失稳载荷2个参量来衡量含缺陷管道的承载能力。当考虑材料应变硬化特性,载荷增加则变形增加,结构发生无限制塑性变形时的载荷就称之为塑性失稳载荷;而假设材料为理想弹塑性材料时,管道所能承受的最大载荷称之为塑性极限载荷,可用ASME规范中的2倍斜率准则来确定。
截止到目前,对于存在腐蚀缺陷的柔性管道承压能力研究很少。本文研究了不同轴向、周向腐蚀长度及小范围的径向腐蚀深度对柔性管道骨架层承压能力的影响。由于骨架层几何尺寸及所受载荷的对称性,为简化模型,节省分析时间,只建立模型进行后续分析。
骨架层材料为316L不锈钢,在20 ℃温度下,屈服强度为210 MPa,抗拉强度为490 MPa,弹性模量E为206 GPa,泊松比为0.3,密度为7.98 g/cm3,伸长率为40%。
在材料参数设置时,选用双线性随动强化模型,切线模量可通过下式进行简化计算。
(6)
式中:Tm为切线模量,MPa;Rm为抗拉强度,MPa;Ys为屈服强度,MPa;l为伸长率,无量纲。将以上参数带入求得切线模量为700 MPa。
本文采用ANSYS Workbench软件对非粘结柔性管道的骨架层进行有限元分析,依据所研究的椭圆度要求建立有限元模型。由于骨架层截面的不规则性,采用扫掠的方式进行网格划分,以骨架层的2个对称截面分别为源面和目标面,首先对源面进行网格划分,然后沿圆周向目标面扫掠,完成实体的网格划分,划分结果如图3a所示。模型节与节之间接触面设置为摩擦接触,摩擦因数为0.15[15];在模型上下两截面施加对称约束,限制其法向位移,两侧边界施加轴向的位移约束,限制其轴向位移,外表面施加均匀压力载荷,如图3b所示。

图3 骨架层有限元模型
塑性极限载荷又称之为垮塌载荷,本文以此为参量来衡量骨架层的承载能力,以无腐蚀缺陷的骨架层分析为例,外表面施加50 MPa均匀荷载,载荷步设置为1,步长为1 000 s,激活自动时间步,时间步类型选择子步,初始载荷步、最小、最大载荷步分别为500、500和1 000。总载荷随载荷子步分步施加,在其逐步施加总变形发生突变,取该突变点位移及应力云图如图4所示。经估算该点施加载荷约为15.95 MPa,明显低于特征值屈曲分析时的临界压溃值,表明对于塑性材料,材料非线性是分析其承载能力必不可少的考虑因素之一,同时也说明在塑性材料的比例极限之前没有失稳情况发生。

图4 无腐蚀缺陷的骨架层仿真云图
通过建立及改变骨架层内表面不同尺寸的矩形凹陷,来模拟实际情况中管道不同的腐蚀缺陷,研究不同缺陷尺寸对管道失效压力的影响,矩形缺陷形貌如图5所示。红色区域为腐蚀坑,XC为轴向长度方向,ZC为周向长度切线方向,YC为径向深度方向。

图5 骨架层局部腐蚀缺陷示意图
所建立矩形腐蚀缺陷尺寸如下:
当轴向长度为3 mm、径向深度为0.5 mm时,缺陷周向长度为17.732 5、35.465 1及53.197 6 mm;当周向长度为35.465 1 mm、径向深度为0.5 mm时,缺陷轴向长度为3、5和7 mm;当周向长度为35.465 1 mm、轴向长度为3 mm时,缺陷径向深度为0.3、0.5和0.7 mm。
采用与无腐蚀缺陷模型同样的步骤进行分析,根据分析结果,依据2倍弹性斜率准则[16]来确定骨架层的塑性极限载荷。在载荷-位移曲线中,斜率为弹性部分直线斜率2倍的直线与曲线的交点即为塑性极限载荷。采用该准则进行计算,结果如图6所示。

图6 局部腐蚀塑性极限载荷的确定
将图6依据2倍弹性斜率准则计算所得数据统计,结果如表2所示。

表2 管道失效压力随腐蚀缺陷尺寸变化情况
由上述分析可知,不同轴向、周向长度及径向深度的腐蚀缺陷都能影响管道骨架层的失效压力,但是影响甚微,可以忽略不计,即小范围的局部腐蚀对骨架层承载能力的影响不大。由于骨架层与运输介质直接接触,考虑其内层缓慢的大面积均匀腐蚀对骨架层失效压力的影响,因为骨架层内表面与所运输的油气水混合介质充分接触,所假设的均匀腐蚀边界如图7所示。

图7 骨架层均匀腐蚀的腐蚀边界
分别以均匀腐蚀深度δ为0.1、0.2、……、0.8 mm的管道骨架层进行承载能力分析,同样运用2倍弹性斜率准则来确定管道的塑性极限载荷,计算结果如图8所示。

图8 均匀腐蚀塑性极限载荷的确定
将图8计算结果整理,结果如表3所示,其中Δp1为相邻两均匀腐蚀深度之间所对应的失效压力差值。

表3 管道失效压力随均匀腐蚀深度变化情况
由表3及图8可知,随着腐蚀深度的增加,骨架层失效压力下降速度整体上逐渐增加,呈现为抛物线趋势,对其进行非线性的拟合,如图9所示。拟合公式为:
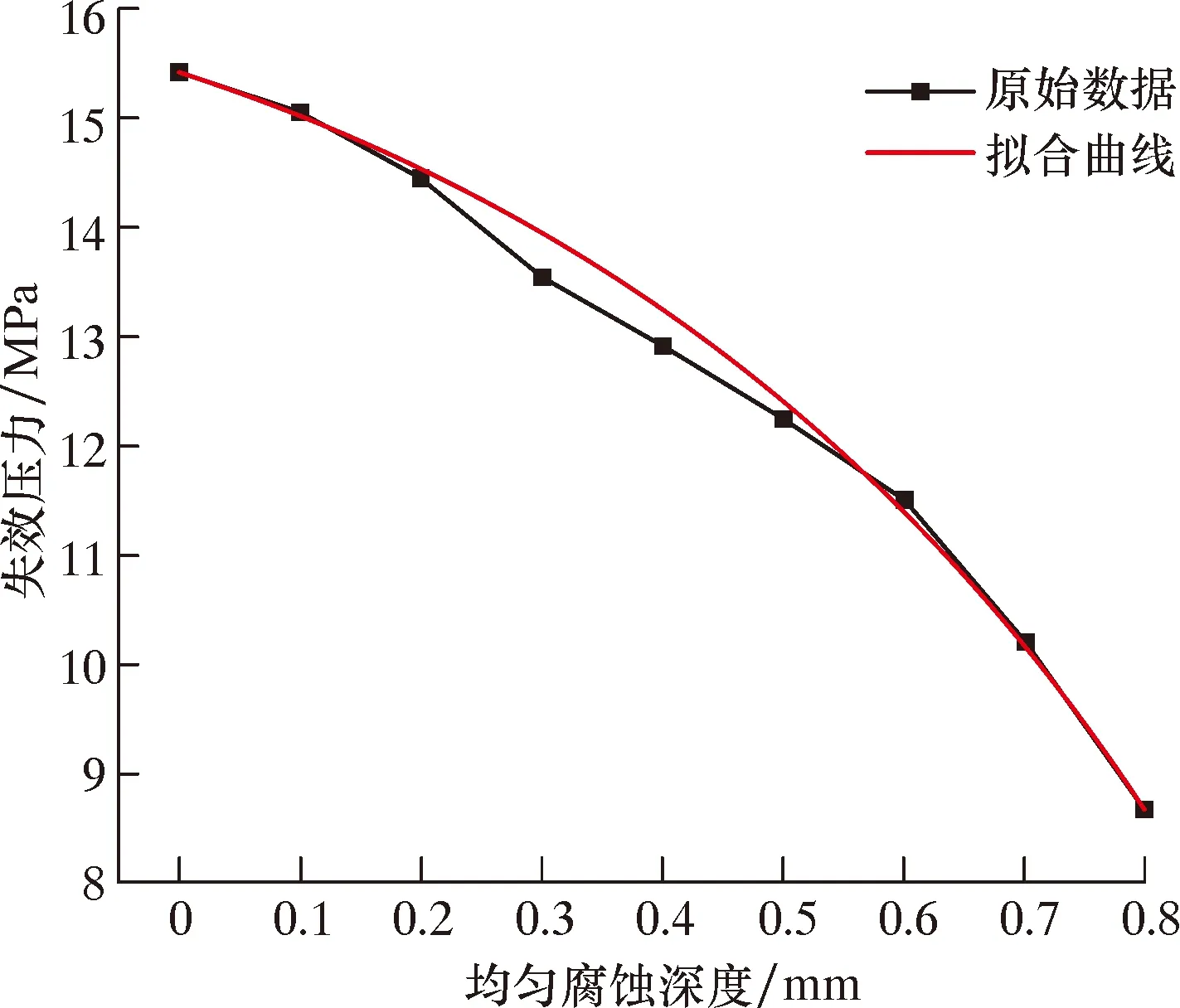
图9 管道失效压力随均匀腐蚀深度变化情况
(7)
式中:y为骨架层失效压力,x为均匀腐蚀深度。
拟合数据及误差如表4所示,经检验,该模型决定系数为0.98,平均绝对误差为0.139 8,均方误差为0.041 4,误差较小,拟合数据符合良好。

表4 拟合数据误差检验
3 腐蚀预测模型建立
海底管道下一时刻的腐蚀状态只与当前时刻有关。马尔可夫性质如下[17-18]:一个随机过程在给定现在及过去所有状态情况下,其下一时刻所处状态的条件概率分布仅取决于当前状态。这与管道的腐蚀状态转移性质相符合,因此可借用离散的马尔可夫过程,即马尔可夫链模型来对管道的腐蚀状态进行预测。马氏链表示如下:
(8)
建立马尔可夫预测模型的关键在于构建状态转移矩阵:
P=[Pij]n×n
(9)
Pij表示系统在t时刻处于状态i,下一时刻(t+l)处于状态j的概率;n为系统所有可能的状态个数。预测模型的建立流程如图10所示。
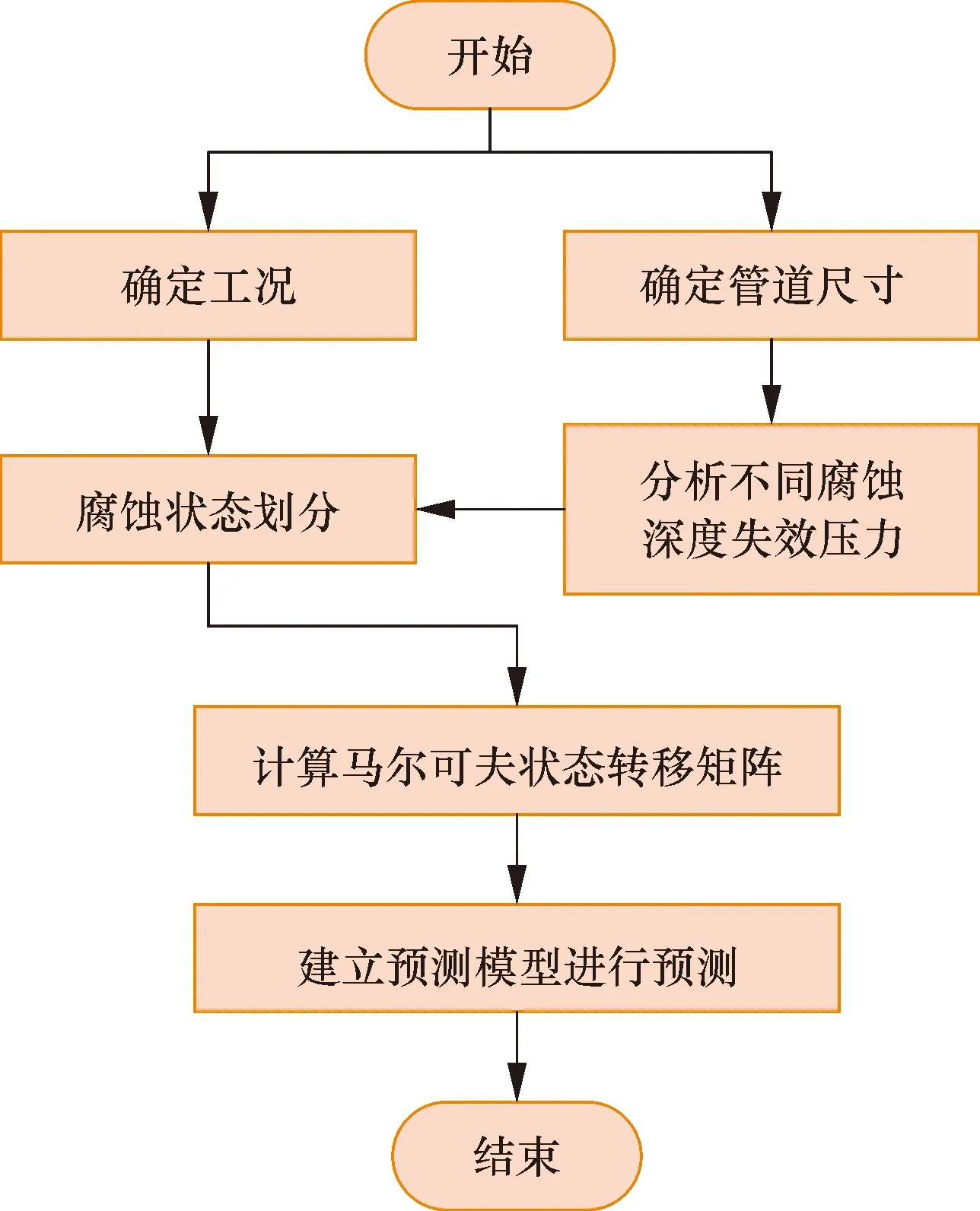
图10 腐蚀预测模型构建流程图
对于传统刚性管道,根据SY/T 6151—2009《钢制管道管体腐蚀损伤评价方法》,以管道的最大腐蚀深度为指标,将不同腐蚀程度的管道划分为“轻、中、重、严重及穿孔”5个等级[19],依次对应5种状态,计算各状态之间的转移概率,可构建马尔可夫状态转移矩阵,实现对管道所处腐蚀状态的预测。而对于非粘结柔性管道骨架层复杂的几何形状,上述状态划分方式明显不适用。依据不同腐蚀深度的骨架层承载能力分析,结合管道所处工况,可进行管道腐蚀状态的划分。以某管道2020—2021年工况为例,该管道输送油气水3项物质,其中输气量(标准状态)为77×104m3/d,输油量、输水量都为4.62 m3/d,内压范围为3.10~4.27 MPa,外压范围为12~15 MPa,出、入口温度分别为25.0和39.2 ℃。
管道不同管段的骨架层承受不同的内压与外压,当某管段内压最小、外压最大时,骨架层承受最大的压力载荷,为11.30 MPa;当某管段内压最大、外压最小时,骨架层承受最小的压力载荷,为7.73 MPa,因此该管道可能承受的压力载荷范围为7.73~11.3 MPa。根据式(7)计算可得,该失效压力区间所对应的骨架层均匀腐蚀深度为0.609~0.854 mm,即当均匀腐蚀深度小于0.5 mm时,管道处于安全状态,定义腐蚀状态为轻度腐蚀;当腐蚀深度处于0.5~0.6 mm之间时,虽然管道失效压力大于工况所施加的载荷,但该阶段的失效压力随腐蚀深度变化较快,有即将失效的风险,定义腐蚀状态为中度腐蚀;当均匀腐蚀深度处于0.60~0.85 mm之间时,管道中某些位置骨架层失效压力小于工况所施加的压力载荷,故定义腐蚀状态为重度腐蚀;当继续腐蚀,腐蚀深度大于0.85 mm时,管道骨架层失效压力小于工况所施加的最小载荷,管道完全失效,定义该阶段腐蚀状态为失效。即该工况腐蚀状态划分如下:①轻度腐蚀,均匀腐蚀深度小于0.5 mm;②中度腐蚀,均匀腐蚀深度在0.5~0.6 mm之间;③重度腐蚀,均匀腐蚀深度在0.60~0.85 mm之间;④失效,均匀腐蚀深度大于0.85 mm。
腐蚀过程中,若不采取措施,劣化状态会越发严重,随着时间的延长,或停留在当前状态,或越来越差,因此状态④,即失效状态只能停留至该状态,不能向其他状态转移,其值为1。根据上述划分的4种腐蚀状态,可得马尔可夫状态转移矩阵如下:
(10)
式(10)中,Pij(i,j=1,2,3,4)为状态转移概率,表示当前时刻为i状态,下一时刻为j状态的概率。已知初始状态为T(0)=[a,b,c,d],其中,a、b、c、d分别为初始时刻管道处于各状态的概率,则n年后管道所处腐蚀状态为T(m)=T(0)×P(n)。至此,完成管道所处腐蚀状态的预测。
4 结 论
基于ANSYS Workbench软件对非粘结柔性管道骨架层进行了特征值屈曲分析,并与理论值作对比。另外,在不考虑螺旋缠绕角度、初始椭圆度为0.2%、考虑材料弹塑性及节间摩擦接触条件下,对腐蚀缺陷形貌及尺寸对骨架层承载能力的影响规律进行了分析,并借助分析结果构建了马尔可夫预测模型,得出如下主要结论:
(1)结合铁木辛柯弹性稳定理论中的圆环挠曲线微分方程,根据单位长度弯曲刚度相等将骨架层等效成截面为矩形的圆环,计算其临界失稳值;建立骨架层有限元模型并对其进行特征值屈曲分析,将分析结果与理论计算结果进行对比,误差为3.02%,验证了理论模型对于无节间摩擦、完美圆状态下弹性材料管道的承载能力计算的可行性。
(2)对于塑性材料,采用理论模型或特征值屈曲方式来进行分析显然不合理,本文以塑性极限载荷为参量来衡量骨架层的承载能力。通过分析矩形腐蚀缺陷的周向、轴向长度及径向深度对骨架层承载能力的影响,发现小范围的局部腐蚀缺陷对其影响不是很大,可以忽略,考虑到骨架层内层与运输介质直接接触,分析了骨架层内层均匀腐蚀对承载能力的影响,分析结果显示该种腐蚀影响较大。
(3)分析均匀腐蚀深度对管道失效压力的影响规律发现,失效压力曲线呈抛物线形式,对其进行非线性拟合,得到均匀腐蚀深度与骨架层失效压力的关系式,经检验,该关系式计算所得结果与仿真结果吻合较好。
(4)在管道腐蚀状态预测时,由于现有的腐蚀状态划分方式对非粘结柔性管骨架层的不适用性,基于分析结果,建立了针对柔性管的腐蚀状态划分新方式,并且建立了马尔可夫预测模型进行预测。
