旋转导向工具多列块式滑动轴承载荷研究*

许爱荣 柳梅梅 薛佳男，2 周 静

(1.西安石油大学机械工程学院 2.昆仑数智科技有限责任公司 3.西安石油大学井下测控研究所油气钻井技术国家工程实验室)

0 引 言

井下旋转导向工具是旋转导向钻井系统的核心组件，旋转导向工具设计一直是该项技术的关键，轴承系统作为其最主要的旋转支撑部件之一，选用的结构类型非常重要[1-3]。旋转导向工具的轴承系统工况十分恶劣，表现在：在导向钻井过程中，钻头压力、导向力和钻具与井眼间的滑动摩擦力综合作用于轴承系统；轴承摩擦副暴露在含有大量固相颗粒的钻井液之中，形成严重的磨粒磨损工况；井底的工作温度可能高达150 ℃以上。随着钻进的进行和井下地层状况的改变，轴承系统所受载荷以及磨损呈现不规则的变化，影响旋转导向工具的导向精确性及稳定性，因而对轴承的强度、抗振和耐磨性能提出了更高要求[4]。近年来，众多学者对旋转导向工具采用的轴承系统进行了研究。ZHANG X.D.等[5-6]研究了旋转导向主轴系统中悬臂轴承的部分载荷效应，提出用深腔滚子轴承代替滚针轴承改善边缘应力集中问题。周琴等[7]研究了旋转导向工具心轴的弯曲变形状态以及对滚针轴承运动的影响。彭松水[8]提出了一种包括推力轴承和向心轴承的导向钻井工具关节轴承组合系统。张光伟等[9-10]对旋转导向可控弯接头变异万向轴的推力滚子轴承与万向轴的相互作用进行了研究，分析了指向式旋转导向钻井工具导向轴的关节轴承固有模态及温度对轴承应力的影响。王涛[11]对旋转导向偏置机构中的PCD滑动止推轴承进行了摩擦磨损特性试验研究，提出了结构参数优化设计方案。王红亮等[4]研究了旋转导向用复合滑动轴承的材料及制造工艺并进行了强度分析。

虽然对轴承系统的研究取得了一定成果，但尝试采用新结构形式的轴承，以适应旋转导向钻井技术的发展仍是未来的研究重点[1]。滑动轴承因具有承载力大、抗振性能好、工作稳定和寿命长等特点[12-13]，在旋转导向工具中将得到更为广泛的应用。笔者针对“ø120.65 mm(4.75 in)高造斜率推靠式旋转导向工具系统研制”项目中采用的多列块式摩擦副滑动轴承结构，应用ANSYS Workbench有限元软件，分析近钻头端径向滑动轴承摩擦副的应力和接触状态，探究轴承摩擦副的载荷变化规律，以期为滑动轴承的设计和使用性能提升提供指导。

1 旋转导向工具滑动轴承系统

推靠式旋转导向工具的机械结构主要包括旋转心轴、不旋转外套、滑动轴承系统、导向机构和下接头等组件。心轴下端与钻头连接，导向机构固定在不旋转外套上，滑动轴承系统置于心轴与不旋转外套之间，依靠轴承系统实现不旋转外套与心轴的相对转动。工具在导向工作时，导向机构的3个翼肋伸出，分别以不同的压力推压井壁，使不旋转外套定位；同时井壁的反作用力对心轴产生一个径向推靠合力，从而达到改变钻进方向的目的[14-17]。

考虑推靠式旋转导向底部钻具组合的第一稳定器对旋转导向工具心轴的约束支撑作用，本文以底部钻具组合第一稳定器至钻头段为轴承系统力学分析的实体模型，模型总长2 854 mm，最大外径(钻头公称直径)152.4 mm。当滑动轴承外圈与内圈的摩擦块呈3块式接触状态时，摩擦块的接触面积最小，轴承摩擦块受力较大，故以此时摩擦副的接触位置建立几何模型。建立的推靠式旋转导向工具轴承系统力学分析几何模型如图1所示。

1—第一稳定器；2、6—滑动轴承系统；3—心轴；4—不旋转外套；5—导向翼肋；7—下接头；8—钻头。

图2为近钻头端滑动轴承组合示意图。由图1、图2可知，工具采用的轴承系统包括2副径向滑动轴承和2副止推滑动轴承，2种滑动轴承分别具有相同的内部结构。径向滑动轴承由外圈和内圈组成，在外圈的外套和内圈的内套上各均匀嵌有4列摩擦块，每列均匀排布30个摩擦块。止推滑动轴承包括定子和转子2部分，定子的空心固定盘和转子的空心转动盘端面上各均匀嵌有单列16个小摩擦柱。径向轴承外套和止推轴承固定盘为一体式结构，通过轴承座固定在不旋转外套上。径向轴承内套和止推轴承转动盘用螺纹连接在一起，分别固定在心轴或下接头上。

1—径向轴承外套；2—外圈摩擦块；3—内圈摩擦块；4—径向轴承内套；5—转动盘；6—摩擦柱；7—固定盘。

为方便摩擦块的位置描述，对径向滑动轴承的摩擦块进行编号，每个摩擦块的编号由“内外圈符号-摩擦副列序号-摩擦块周向位置序号”组成。轴承内圈用ip表示，外圈用op表示；摩擦副的列编号用“Ⅰ～Ⅳ”表示，近导向翼肋侧为第Ⅰ列摩擦副，其他列依次排序；摩擦块的周向位置序号编排如图3所示，编号用数字“1～30”表示，起止位置见图3，按顺时针方向依次增大，称“1～15”号为上半圈摩擦块，“16～30”号为下半圈摩擦块。如编号“ip-Ⅰ-2”，表示位于轴承内圈、第Ⅰ列上半圈的第2个摩擦块。图3中F表示翼肋推力合力(简称翼肋推力)及作用位置。

图3 单列摩擦块编号示意图

相较于两端的止推滑动轴承，径向滑动轴承将承受钻压和翼肋推力同时作用产生的径向力，特别是近钻头端径向滑动轴承位于导向翼肋和钻头之间，载荷环境更为苛刻，其摩擦副承载特性的研究尤为重要。本文采用ANSYS Workbench软件进行近钻头端径向滑动轴承多列摩擦副应力计算时，摩擦块的摩擦接触非线性问题求解采用Augmented Lagrange方法。

2 Augmented Lagrange算法

求解摩擦接触问题通常采用的方法有罚函数法、Lagrange方法和Augmented Lagrange方法。Augmented Lagrange方法应用于摩擦接触问题时，克服了罚函数法中罚参数及优化参数的不确定等缺点，也消除了传统Lagrange方法中增加系统求解规模的缺点[18]。Augmented Lagrange方法处理摩擦接触问题的过程如下。

根据库仑摩擦定律，设滑动函数为φ，两物体接触的切向约束条件可表示为：

(1)

式中：μ为摩擦因数；pn为法向接触力，MPa；pt为摩擦接触力，MPa；ut为切向位移，m；ξ为滑动量,m。

当φ<0、ξ=0、dut=0时，为完全黏着接触状态；当φ=0、ξ>0、dut≠0时，为相对滑动接触状态。

假设允许物体间存在穿透，即接触处的法向位移gn<0，法向接触力可表示为：

(2)

式中：λn为法向拉格朗日乘子，MPa；εn为法向罚因子，MPa/m。

将摩擦接触力增量dpt分解为罚部分和拉格朗日乘子部分dλt，则接触点切向约束条件可表示为：

(3)

式中：εt为切向罚因子，MPa/m;λt为切向拉格朗日乘子,MPa。

(4)

(5)

3 建立有限元分析模型

滑动轴承系统的多列摩擦块选用YG8硬质合金材料，摩擦柱选用聚晶金刚石材料，轴承系统力学分析模型的其余零部件材料均选用P550无磁钢。各组件材料的力学性能参数如表1所示。

表1 各组件材料的力学性能参数

把图1几何模型导入ANSYS Workbench软件之中，用不同单元尺寸控制网格精度以划分网格，并进行网格精度的计算验证，划分的单元总数为327 520。滑动轴承多列摩擦副之间的接触为非对称接触，指定接触面为内圈摩擦块的外表面，目标面为外圈摩擦块的内表面，接触单元数为10 864。接触算法选用Augmented Lagrange法。

将旋转导向工具轴承系统力学分析模型视为简支梁[19]，在图1的第一稳定器端面施加纵、横方向位移约束，钻头端面施加横向位移约束，在导向翼肋表面施加与工具重力方向相反的翼肋推力F，钻头端面施加钻头压力W，工具自重为分布体力。

4 轴承摩擦副应力计算结果分析

应用ANSYS Workbench有限元软件，基于建立的有限元分析模型，考虑几何非线性效应，在钻头压力W=200 kN，翼肋推力F分别为10和25 kN的2种载荷工况下，进行模型的力学计算，可得到滑动轴承摩擦副在2种载荷工况下的等效应力(von Mises应力)、接触压应力及摩擦应力。由计算结果可知，在2种载荷工况下，模型的最大应力值分别为73.121和223.37 MPa，最大应力均发生在摩擦副上，且远小于选用材料的屈服极限，满足强度要求。

4.1 轴承各列摩擦副最大应力分布

4.1.1 轴承内圈各列摩擦块

2种载荷工况下轴承内圈各列摩擦块的应力极值列于表2中。表2中，应力极值差等于相同载荷工况下最大应力的最大值与最小值之差；最大应力比值为F=25 kN与F=10 kN工况下各列摩擦块最大应力的比值。最大应力分布曲线如图4所示。由表2及图4可以看出：

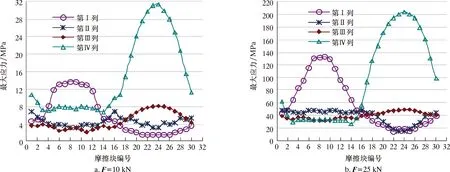
图4 轴承内圈4列摩擦块的最大应力分布曲线

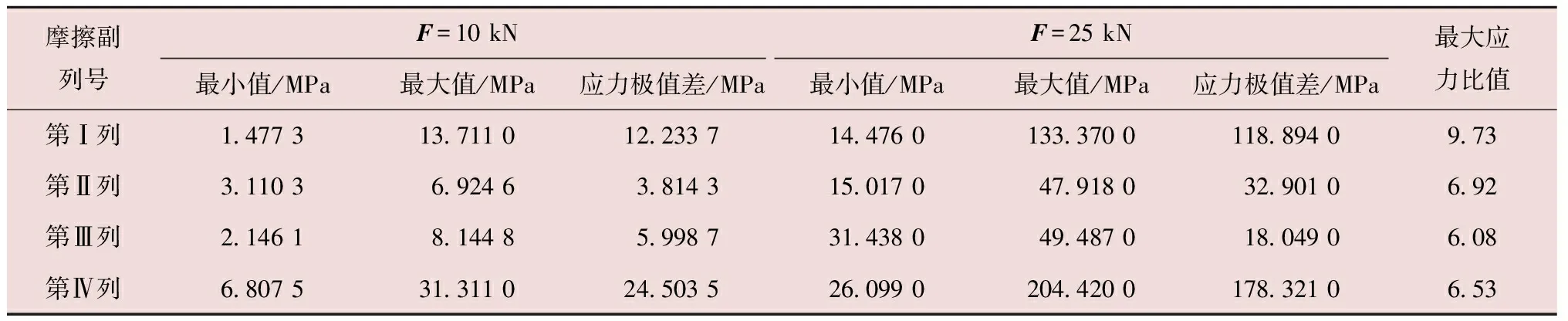
表2 内圈各列摩擦块的最大应力极值

(1)2种载荷工况下，各列摩擦块的最大应力分布规律基本相同，位于第Ⅰ列上半圈、第Ⅳ列下半圈摩擦块的最大应力呈上凸状曲线分布，变化幅度较大，应力极值差最高达178.32 MPa；第Ⅱ、Ⅲ、Ⅳ列上半圈的各列摩擦块最大应力近似呈现水平直线分布，应力波动甚小。

(2)内圈各列摩擦块的最大应力均随翼肋推力的增大而增大，各列摩擦块最大应力增大到6倍以上，翼肋推力的增大使第Ⅰ列上半圈、第Ⅳ列下半圈摩擦块的应力水平快速上升，第Ⅳ列摩擦副分担的外载荷最大，编号为ip-Ⅳ-24的摩擦块应力最大为204.42 MPa。

(3)在旋转导向工具工作时，内圈摩擦块随心轴一同旋转，因此，各摩擦块的最大应力将随其周向位置的变化按应力曲线的分布规律循环变化，处于周期性交变应力状态；当翼肋推力较大时，第Ⅰ、第Ⅳ列摩擦副将承受高幅值的循环应力，即靠近翼肋处和靠近钻头处的摩擦副应力受外载荷的影响更大。

4.1.2 轴承外圈各列摩擦块

2种载荷工况下轴承外圈各列摩擦块的应力极值列于表3中。表3中的应力极值差及最大应力比值与表2定义相同。最大应力分布曲线如图5所示。由表3及图5可以看出：

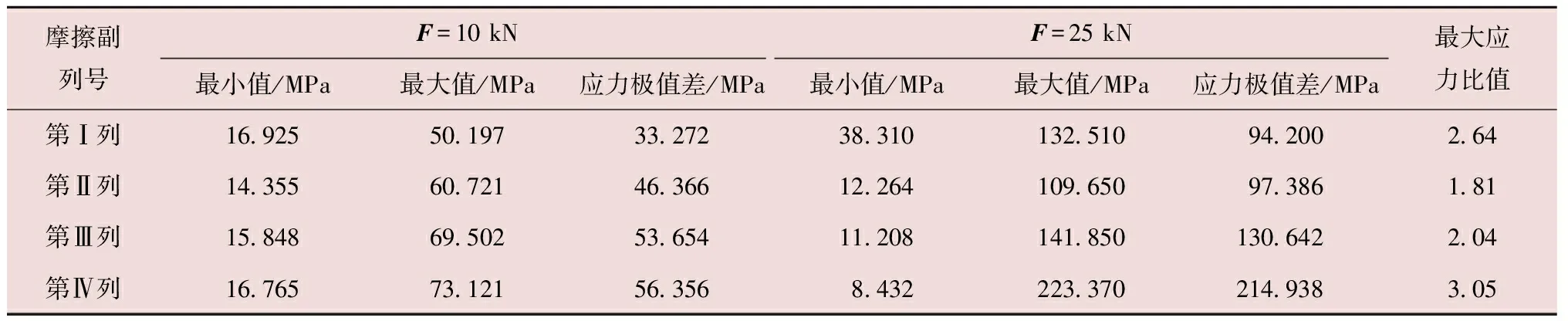
表3 外圈各列摩擦块的最大应力值

图5 轴承外圈4列摩擦块的最大应力分布曲线

(1)2种载荷工况下，第Ⅱ～Ⅳ列摩擦块的应力分布规律基本相同，上半圈摩擦块的应力曲线呈下凹状或盆状，下半圈应力曲线呈上凸状，从摩擦副圆周顶部至底部，摩擦块的应力逐渐增大；上半圈各列摩擦块的应力分布曲线趋于重合。

(2)随着翼肋推力的增大，第Ⅰ列上半圈摩擦块的应力曲线变化规律与其他3列不同，翼肋推力的增大使上半圈顶部附近的摩擦块应力水平上升较快，曲线由下凹转为上凸状；下半圈摩擦块应力分布规律的变化与其他3列相同。

(3)随着翼肋推力的增大，各列摩擦块的最大应力均增大，最大应力比值大于1.8；第Ⅳ列摩擦块的应力水平上升最快，承担外载荷最大，位于圆周底部编号为op-Ⅳ-23的摩擦块应力最大为223.37 MPa。

(4)对于静态推靠式旋转导向工具，外圈摩擦块不旋转。因此，外圈周向不同位置的各摩擦块应力水平始终保持不变，各列摩擦块的最大应力极值差越大，应力分布就越不均匀。显然，第Ⅳ列摩擦块应力分布的不均度最大，在翼肋推力为25 kN时，最大应力差值高达214.94 MPa。

4.2 轴承摩擦副总体应力分布

图6为2种载荷工况下滑动轴承多列摩擦副的应力云图。图7给出了翼肋推力为25 kN条件下，轴承内圈各列中最大应力摩擦块的应力云图。

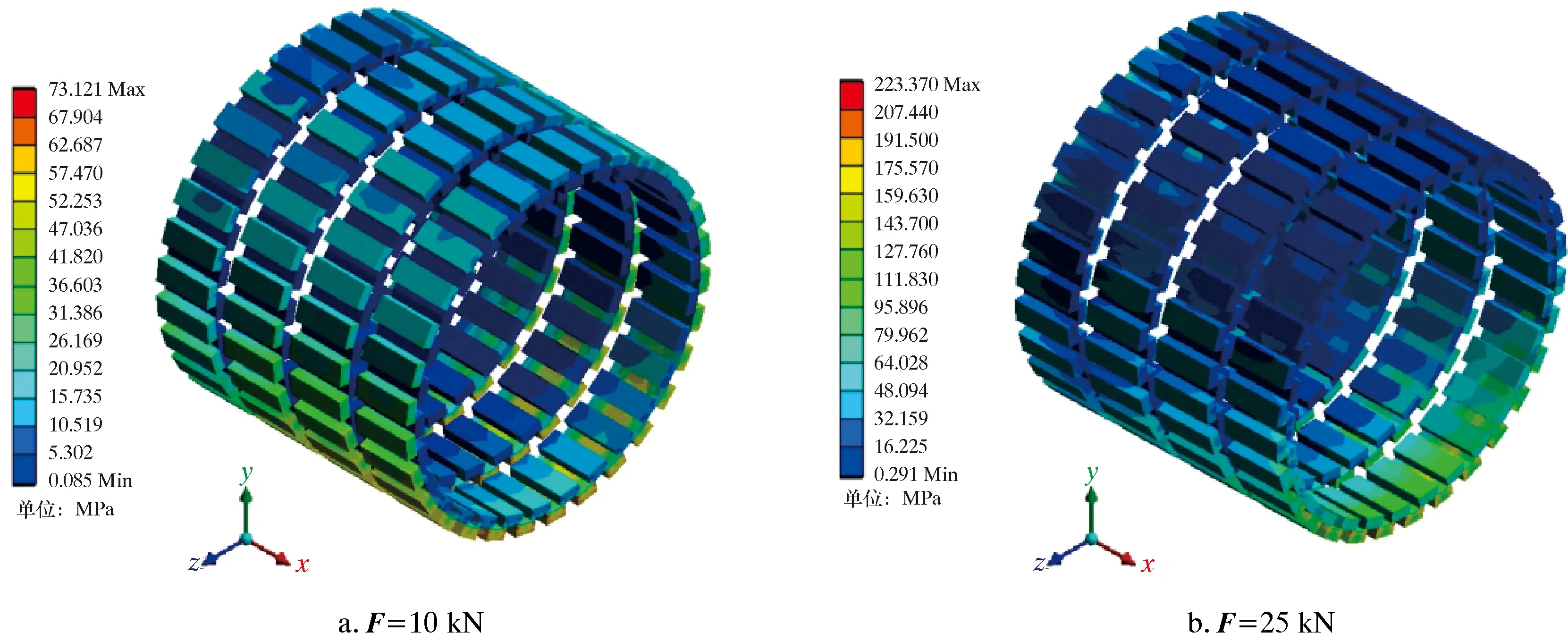
图6 近钻头滑动轴承多列摩擦副应力云图

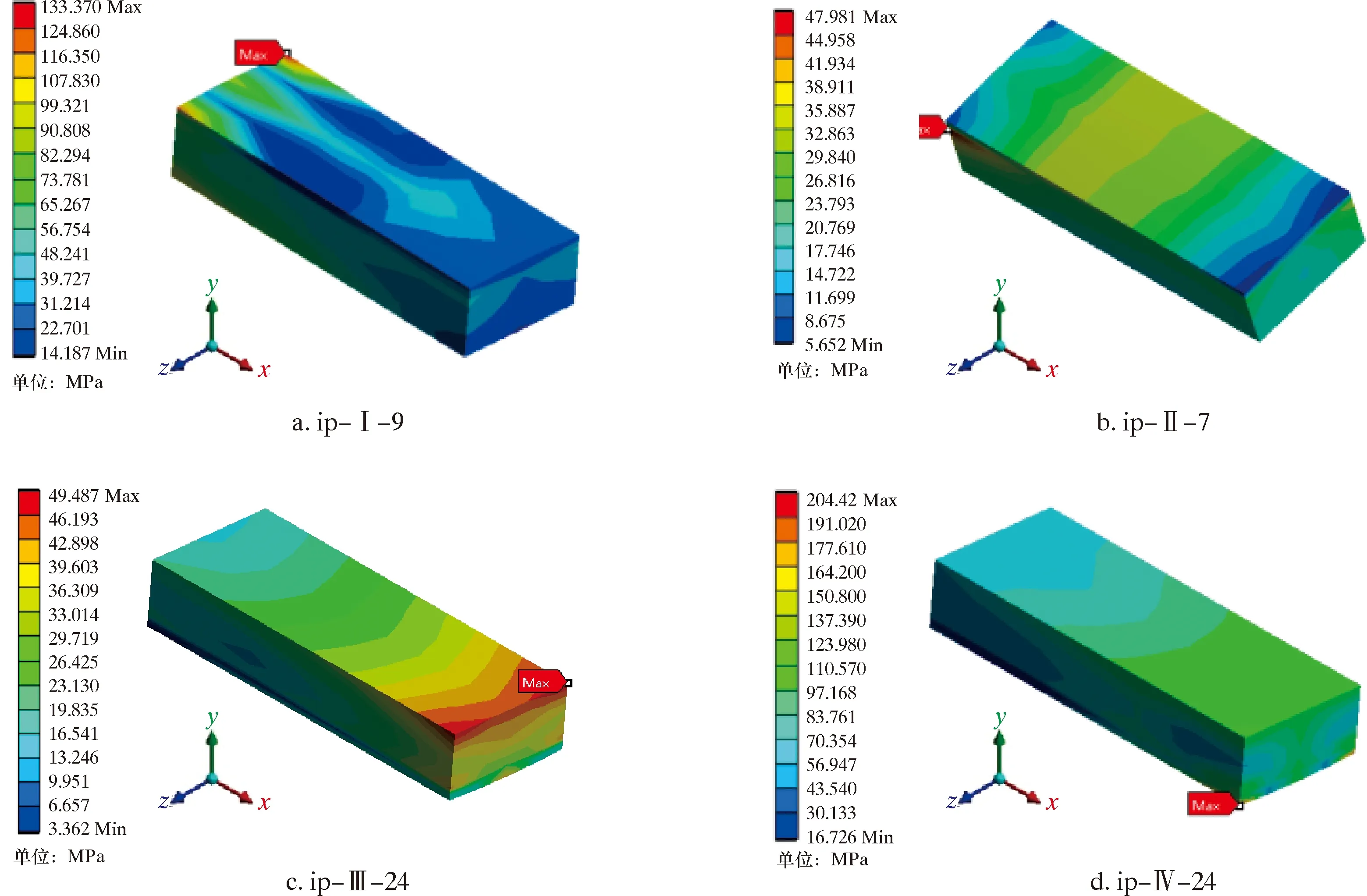
图7 内圈各列最大应力所在摩擦块的应力云图

由图6和图7可以看出，内、外圈各列周向相同位置的摩擦块应力分布明显不同，翼肋推力的变化改变了内、外圈同一位置摩擦块应力大小的相对关系。摩擦块的较大应力区域从第Ⅰ列的左端渐渐地移向第Ⅳ列的右端区域，即轴承各列最大应力摩擦块的最大应力位置由近翼肋端逐渐向近钻头端变动；内圈第Ⅰ、Ⅱ、Ⅳ列摩擦块的接触表面应力较大，第Ⅲ列摩擦块的嵌入内套面应力较大，即多数摩擦块的摩擦接触表面应力较大，最大应力均发生在摩擦块的边角处。

上述轴承各列摩擦副最大应力分布曲线以及应力云图的变化特性是翼肋推力、钻头压力、端部约束及工具几何的综合作用导致。图8为翼肋推力为25 kN条件下轴承系统有限元力学分析模型的整体变形云图。由图8可以看出，不旋转外套与轴承内、外圈的变形不一致，造成轴承不同位置摩擦块的应力和接触状态不同，影响各摩擦块的载荷大小。

图8 轴承系统力学分析模型的位移云图

5 结论及认识

(1)推靠式旋转导向工具的近钻头径向滑动轴承内圈各列摩擦块在2种载荷工况下的最大应力分布规律基本相同。位于第Ⅰ列上半圈、第Ⅳ列下半圈的摩擦块应力水平及变化较大，应力水平明显高于其他2列，第Ⅱ、Ⅲ列摩擦块的应力水平与变化较小。

(2)在2种载荷工况下，径向滑动轴承外圈第Ⅱ～Ⅳ列摩擦块的最大应力分布规律基本相同，位于上半圈摩擦块的应力水平及变化范围较小，下半圈摩擦块应力水平及变化范围明显增大。翼肋推力的增大，使第Ⅰ列上半圈顶部附近的摩擦块应力水平上升较快，周向顶部的摩擦块应力高于底部，改变了第Ⅰ列摩擦块的应力分布规律。

(3)翼肋推力的增大，增大了轴承内、外圈摩擦块的最大应力，内圈各列摩擦块的最大应力增大到6倍以上，外圈摩擦块的最大应力增大到2倍左右；第Ⅳ列摩擦副的应力增幅远高于其他3列，内、外圈摩擦块最大应力的增量分别达178.32及214.94 MPa，最大应力均发生在该列底部的摩擦块上，内、外圈摩擦块的最大应力分别为204.42及223.37 MPa。第Ⅰ列、Ⅳ列摩擦副的应力水平及分布受外载荷的影响最大，当翼肋推力较大时，第Ⅳ列摩擦副承担的外载荷最大，第Ⅰ列摩擦副次之，即靠近翼肋处和靠近钻头处的摩擦副应力受外载荷的影响较大。

(4)轴承外圈各列摩擦块的载荷大小与主导向翼肋的周向相对位置有关，内圈各摩擦块的最大应力呈周期性变化，易产生疲劳破坏。因此，轮换3个翼肋与造斜方向的相对位置均衡外圈摩擦块载荷、选择高疲劳强度的内圈摩擦块材料、改进循环应力幅值较大列摩擦块的结构设计，可达到减轻轴承振动、预防摩擦副失效、延长轴承使用寿命的目的。