旋转导向推力测试装置设计优化*
2022-02-13张玉霖贾建波杨恒灿菅志军丁旭东
张玉霖 卢 涛 贾建波 杨恒灿 菅志军 丁旭东
(中海油田服务股份有限公司)
0 引 言
旋转导向钻井系统[1-5]是当代定向钻井技术发展的最新成果,是目前油气勘探开发行业最先进的定向钻井技术装备。其可在全井段保持旋转钻进,并根据需要及时调整轨迹,实施三维定向井轨迹控制,具有精准命中靶区、建井周期短、钻井质量高、大幅提高采收率等特点,代表着当今世界钻井技术发展的最高水平,被誉为石油钻井技术“皇冠上的明珠”。该技术最早诞生于20世纪90年代,一经问世就引起了钻井作业者的极大关注,随着技术的不断成熟和产品的应用推广,每年全球市场规模达到了80亿美元左右,占到了定向钻井市场的75%以上。
近几年,国内旋转导向技术发展迅猛,中海油、中石油、中石化等多家单位开展了技术攻关和产品研制。其中中海油的进展最具代表性,开发出了全系列商业化技术装备,产品应用规模迅速提升,已经突破1 000井次、100万m进尺应用大关,呈现出了良好的发展势头。中国作为油气资源需求大国,该技术对提升油气产量和保障能源安全具有十分重要的意义。
旋转导向钻井系统按其工作原理可以分为推靠式(push-the-bit)和指向式(point to the bit)2种。推靠式属于被动式导向工具,工具的导向性能与推靠效果高度相关,对地层依赖较大。指向式属于主动式导向工具,对地层依赖较小;2种系统各有特点,研究并提升系统的测量及控制精度对提升旋转导向的应用效果至关重要。笔者针对推靠式旋转导向推靠力测试需求,设计了推靠力测试装置,并对测试装置存在的若干问题进行研究,对测试装置进行了设计优化,可大幅提升系统的控制精度和应用效果。
1 推靠力与导向力矢量关系
推靠式旋转导向钻井系统的推靠功能主要由偏置短节[6-11]实现。在偏置短节的外圆上周向均布3个独立的推靠臂(见图1中推靠力F1、F2、F3),3个推靠力互成120°,3力平面汇交[12-17],其合力F的方向α可按公式(1)来计算,导向力矢量与合力F大小相等,方向相反。

图1 平面三力汇交力系合力计算
(1)
式中:F1、F2、F3为3个推靠力,N;F为3个推靠力的合力,N;θ0为F1与X轴正向的夹角,(°);α为合力F与X轴正向的夹角,(°)。
合力的方向、大小由3个分力决定,分力的测控误差会对合力的大小和方向产生很大影响。假设F1、F2、F3分别为1 000、1 000、1 200 N且F2测控误差范围从10%至30%,为了计算方便,假设θ0为0°,计算数据见表1。由表1可见,F2测控误差为30%时,合力的角度误差达到了36.59°。

表1 分力误差引起的合力角度误差
2 推靠力测试系统研制
2.1 系统构成
推靠力测试系统由1个测力盘、3组推力传感器、信号采集处理模块及测控监视系统构成(见图2)。通过压差传感器可以算出3个推靠臂的理论推力,通过推力传感器可以测量3个推靠臂实际推力,对比可知两者的差值,并建立压力与推靠力的线性关系。
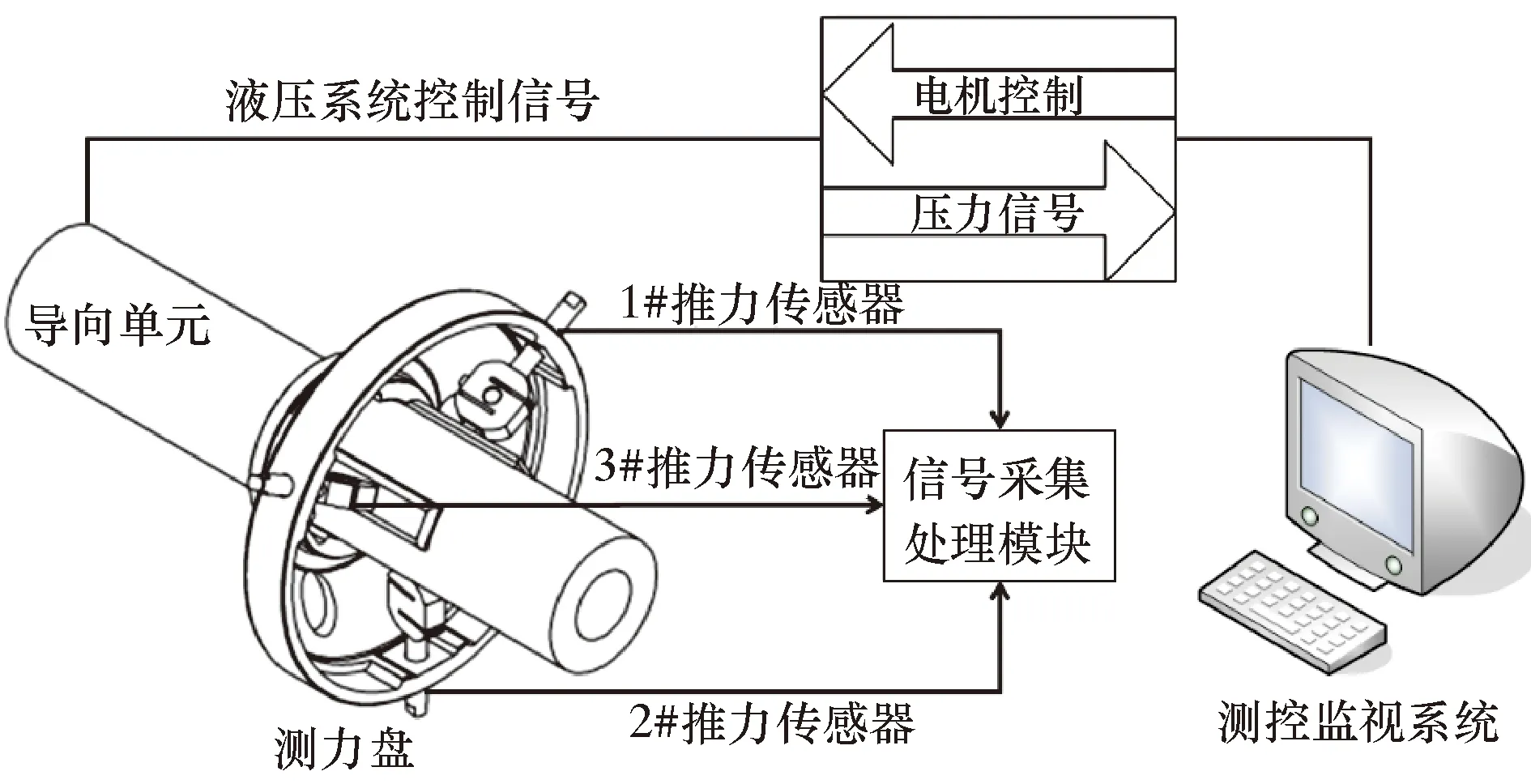
图2 推靠力测试系统
2.2 测试试验
图3为推靠力测试系统实物照片(这里将优化前的测力盘称为A),利用该系统先对一个推靠臂进行推靠力测试,检测其理论推力与实际推力的偏差情况及推靠力与压力的线性关系,再同时进行3个推靠臂的推力测试。

图3 推靠力测试系统实物及测量模型
图4为1个推靠臂的测试曲线。由图4可以看出,实测推力和理论推力之间存在一定差值,且随着推力增大,差值也变大,差值最大达到5 kN。

图4 实测推力-理论推力关系曲线
图5是3个推靠臂推力同时测试的曲线。设置1#、2#和3#推靠臂的推力分别为推力1、推力2和推力3。对1#推靠臂从0~24 MPa进行一个完整的升程和降程的推力测试,设置2#、3#推靠臂的压力为0,则2#和3#的实测推力应该为0,但实际结果却并非如此。从图5可以看出,2#、3#的实测推力会随着1#推靠臂压力的升高而逐渐变大,这说明1#推靠臂的推力对2#和3#推靠臂造成了影响。用相同的测试方法对2#和3#进行单独的推力测试,也发现了同样的情况。
对单独推靠臂和3个推靠臂同时推力测试发现,该测试系统存在以下2个问题,极大地影响导向力测控精度,必须加以分析解决:单个推靠力测量精度较低,实测推力和理论推力存在较大偏差;测力盘A变形引起的3个推靠臂推力测量相互干扰,极大地影响推力测量精度。
2.3 结果分析
针对上述问题,对系统各部件的受力情况进行分析,可以初步锁定问题的根源在于测力盘A的变形过大。测力盘A进行单路推力测量时受力变形如图6所示。测力盘A可以简化为一个悬臂梁,主要有5个方面的变形因素:测力传感器变形X1,测力盘A变形X2,安装固定变形X3,推靠臂受压变形X4和传感器固定杆变形X5。系统总变形量可以表示为:

图6 测力盘进行单路推力测量时受力变形示意图
X=X1+X2+X3+X4+X5
(2)
式中:X为测试系统受力总变形量,mm。
理想情况下,希望X=X1,这样使得变形更多地反映在传感器上,虽然实际上X2、X3、X4、X5无法完全消除,但却可以使其尽量减小。由胡克定律可知,材料受力变形量取决于4个因素:力、长度、弹性模量和面积。只要选用高强度材料,增加固定螺栓的直径、缩短螺杆的长度,便可大大减小这4方面的变形量,使X1所占比重越大,测量的准确度也就越高。
2.4 主要零部件有限元分析
对测力盘A、推靠臂、传感器固定杆、固定螺栓4种零件赋予同样的材质,这里选用40Cr。这样做的目的是为了便于对各因素的受力变形量进行比较。40Cr的材料属性见表2。

表2 40Cr力学属性
运用有限元软件对4个零件的变形逐一进行分析,首先对测力盘A进行受力变形分析,分析结果如图7所示。

图7 测力盘A受力变形的有限元分析
按照上述方法依次对传感器固定螺栓、安装固定螺栓、推靠臂进行分析。将4个零件的变形进行对比,结果见表3。由表3可以看出,对每个推靠臂进行单独测量时,测力盘A是主要变形因素,变形量占到了84%,其余变形量则远远小于X2,可以忽略不计,测力盘A的变形是影响测量精度的主要因素。由此可知:只要设法减小测力盘A的变形量,就可大大减小推靠臂实测推力与理论推力之间的差值,从而提高系统的测试精度。

表3 4个次要零件变形情况对比
单个推靠力测试时测力盘A的应力和变形分布见图8。由图8可以看出,1#推靠力引起的变形延伸到了相邻2个传感器(即2#和3#传感器的安装位置),用探针拾取2#传感器安装位置附近5个点处的变形量,见表4。由表4可以看出,从1#到2#传感器的相邻区间,5个点变形量逐渐减小,2#传感器的正对位置(节点19922处)变形量为0.075 mm,这种影响在3个推靠力同时测量时表现尤为明显。

图8 测力盘A变形扩散分布

表4 测力盘A测力点附近5个节点变形量
综上所述,测力盘A的变形是影响系统测试精度的主要原因,优化测力盘A的结构以减小变形量和相互干扰是改进测量效果的主要方向。
3 测试系统优化
3.1 测力盘结构优化方案
原有测力盘A呈喇叭状,采取小端固定的方式,传感器受力时,测力盘相当于一个悬臂梁(见图9)。由材料力学可知,在相同结构参数下,简支梁的挠度是悬臂梁的,变形量大幅降低。

图9 测力盘受力模型
基于这一思路,在测力盘A的基础上,设计了一种新结构的测力盘B,见图10。测力盘B呈纺锤状,伸出3个桥状翼肋,用于安装测力传感器。采用两端同时固定的方式进行安装,每2个测力桥之间设计一条加强筋,进一步加强测力盘的结构强度。

图10 测力盘B三维模型
3.2 优化结构有限元分析
对优化后的测力盘B进行有限元受力分析,材质依然选用国标40Cr。先进行单个推靠力测试的受力分析。再进行3个推靠力同时测试的受力分析,将测力盘B的变形与测力盘A的变形进行对比,结果见表5。由表5可知,测力盘B的变形大幅减小,仅为测力盘A变形的2.67%,优化效果非常明显。

表5 测力盘A和测力盘B变形量对比
将测力盘B的变形与其余几个零件的变形进行对比,结果见表6。由表6可知,测力盘B的变形量与其余3个干扰因素的变形量相当。测力盘的变形占比从之前的84%下降到12.5%。
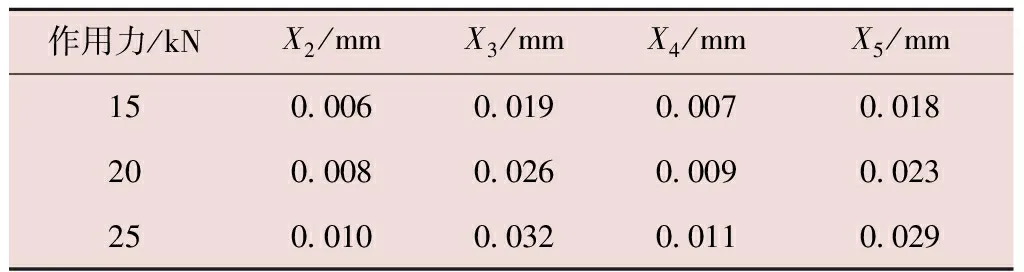
表6 测力盘B受力变形量对比
3.3 测试试验
对测力盘B进行推靠力测试试验,结果见图11。由图11可知,实测推力和理论推力之间的差值约为0.9 kN,比测力盘A的测试差值5 kN小了80%左右,说明优化后的测力盘B确实减小了理论推力和实测推力之间的偏差,优化效果非常理想。

图11 测力盘B理论推力-实测推力曲线
同2.2设置推力1、推力2和推力3,对1#推靠臂进行推力测试,压力从0~24 MPa进行一个完整的升程和降程,设置2#、3#推靠臂的压力为0,结果见图12。由图12可知,1#推力随着1#设定压力的增大呈线性增加,2#和3#推力则没有任何变化,说明了优化后的测试系统不会相互干扰。
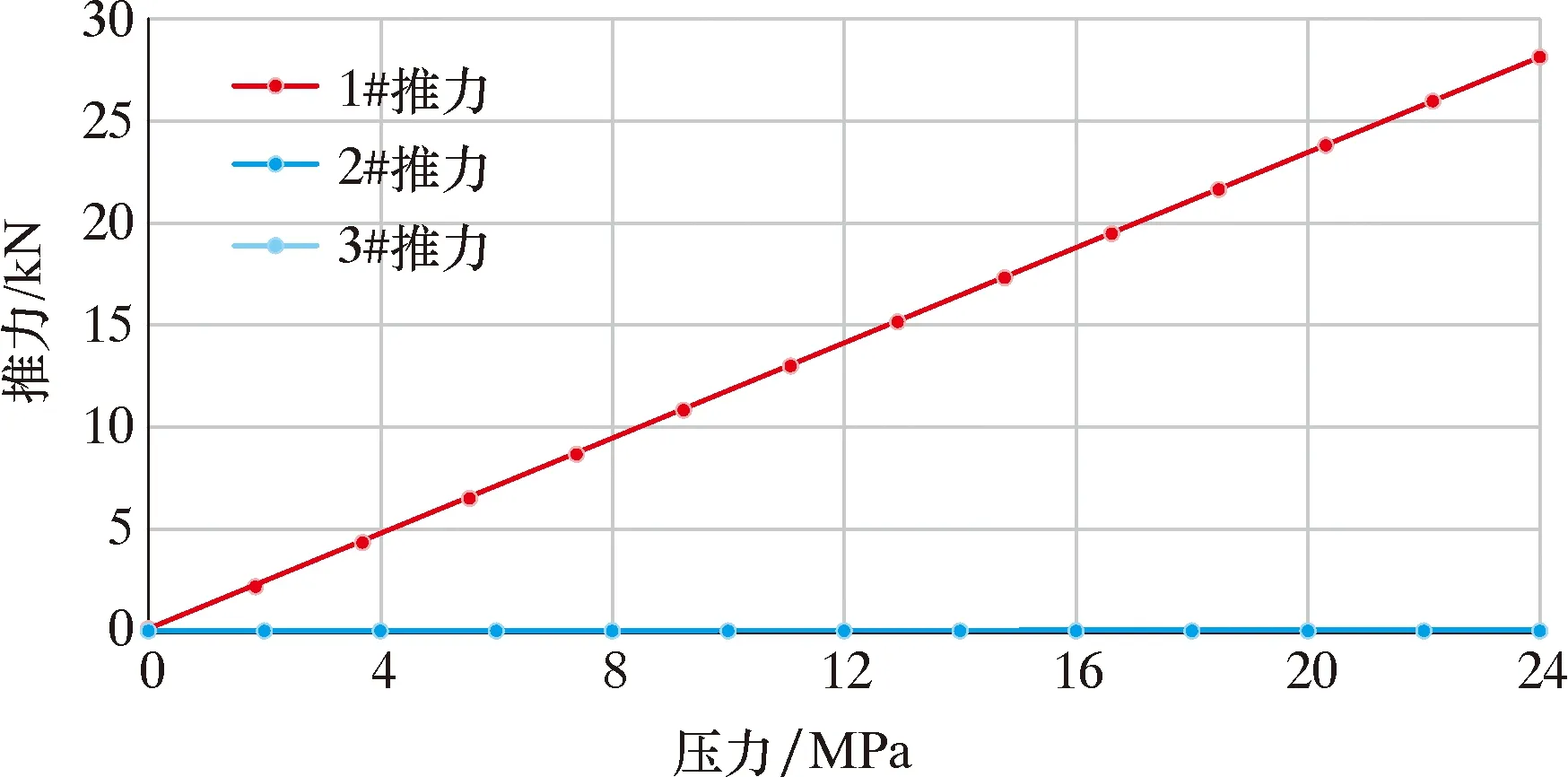
图12 单个推靠力测试时3个实测推力的变化趋势
4 结 论
(1)阐述了推靠式旋转导向的工作原理,并针对推靠式旋转导向钻井系统推靠力测试需要,设计了一种测试系统,实现了推靠力测试及标定功能。
(2)进行了推靠力测试试验,对试验中出现问题的原因进行了深入分析,找出了影响测量精度的关键因素;并运用有限元软件对各个零件受力变形情况进行分析,分析结论与试验问题相互印证。
(3)根据分析结果对测力盘结构进行了优化,再次运用有限元软件对优化结构进行仿真分析。仿真结果显示,优化结构大大降低了测力盘的变形量和互相干扰,解决了3个推靠臂推力测试相互干扰,导致测量精度低的问题,优化结果在后续的试验测试中得到了很好地验证。
(4)所研制的推靠力测试装置实现了推靠力的精确测量,为导向力的精确测控奠定了基础,该测试系统已成功应用于仪器制造和使用,成为旋转导向技术装备产业化必备的测试设施之一。
