全向移动机器人的自抗扰轨迹跟踪控制

张相胜，黄将

（江南大学轻工过程先进控制教育部重点实验室，江苏无锡214122）

传统轮式移动机器人在平面运动中属于非完整约束系统，一般仅适合于空间较大，转向灵活性不高的场合[1]。而全向移动机器人（Omni-directional mobile robot，ODMR）的优势在于运动过程中不需要改变自身位姿，仅依靠全向移动机构即可实现任意方向移动，适合在狭窄的空间，精度要求较高的场合，如物流搬运、救灾、侦查地形等[2]。常见的全向移动机构有：Mecanum 轮、球轮、连续切换轮、正交轮、偏心轮等[3]。其中，以Mecanum 轮作为行走机构的ODMR 结构简单实用，平移运动灵活自如，因此它的机械结构、力学模型、运动控制等方面受到许多国内外学者的关注，尤其是针对ODMR 轨迹跟踪问题成为近几年的研究热点。

目前，轮式移动机器人轨迹跟踪的控制方法主要有PID控制、自适应滑模控制、模糊控制、神经网络控制、自抗扰控制[4-8]，以及这几种控制方法的相互结合，如自适应反步滑模控制、模糊自适应滑模控制、自适应神经网络滑模控制等[9-11]。PID控制虽然较简单，但对复杂的非线性耦合系统的控制效果并不理想；自适应滑模控制和模糊控制均具有一定的鲁棒性和自适应性，但前者的输出易出现抖振，后者模糊规则的选择缺乏系统性，且无法在线调整；神经网络控制有较好的鲁棒性，但控制算法复杂，在线学习时间长；而自抗扰控制不需要依赖被控对象的精确模型，仍可对系统集总扰动进行精确的估计补偿，且结构简单，计算量小[12-13]，因此在移动机器人领域得到了广泛应用。

本文主要研究了4-Mecanum 轮ODMR 在未知干扰下的轨迹跟踪问题。首先，建立了ODMR 的运动学和动力学模型，然后设计了改进的扩张状态观测器和自抗扰动力学控制器，最后通过仿真对比结果验证了本文控制器的优越性。

1 动力学建模

1.1 运动学分析

图1为本文所设计的4-Mecanum ODMR，各轮分别由一台直流电机独立驱动，结构布局为纵向对称分布，由于各轮速矢量均可被分解至 XM和 Yu方向上，因此只需调节4个轮子的转速方向，就可以在水平面上实现三自由度的平面运动。

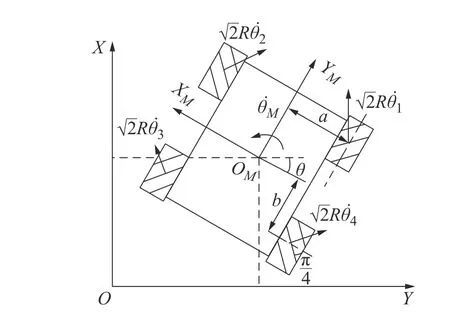
图1 全向移动机器人坐标系

假设：1）ODMR 在绝对平坦的地面上运动，各轮不存在打滑或空转现象；2）ODMR 的重心与自身几何中心重合。以大地作为广义坐标系O（X,Y），以ODMR 的几何中心为原点的移动坐标系为OM（XM,YM），由此建立ODMR 逆运动学方程为[14]：

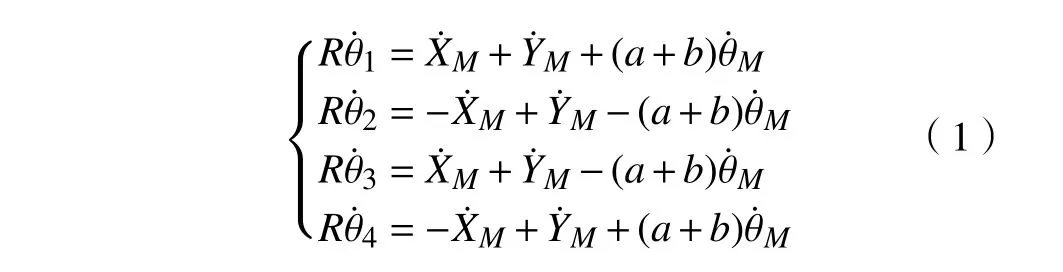
将式（1）写成正运动学矩阵方程为

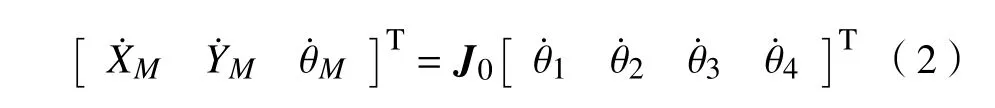
式中J0为ODMR 的雅克比矩阵。

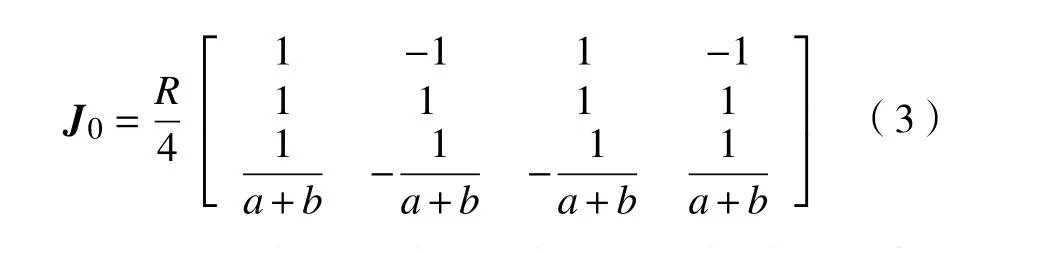
设移动坐标系到广义坐标系的坐标转换矩阵为E，则ODMR 在广义坐标系下的位姿为

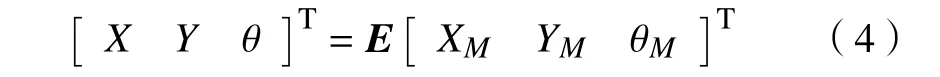
联立式（2）与式（4）得到ODMR 在广义坐标系下的正运动学方程为

1.2 动力学分析

ODMR 属于多刚体系统，可根据拉格朗日方程描述其动力学模型为[15]

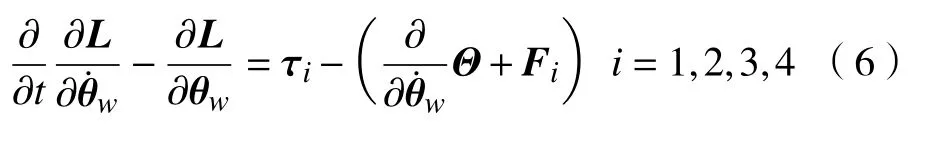
由于机器人只做平面运动，选取重心所在平面为零势能面，即V =0，可得到拉氏函数为

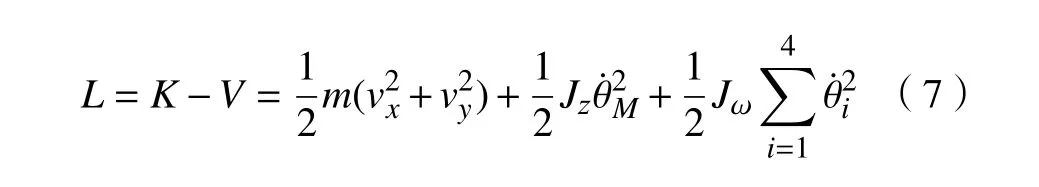
式中：K 为总动能； m为 机器人的总质量； Jz为机器人绕 z 轴的转动惯量； θ˙z为机器人绕 z轴旋转的角速度；Jω是各轮绕轮轴的转动惯量；速度分量vx=，vy=

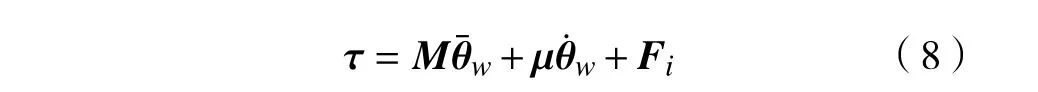
联立式（2）、式（6）与式（7）可得系统的动力学方程为

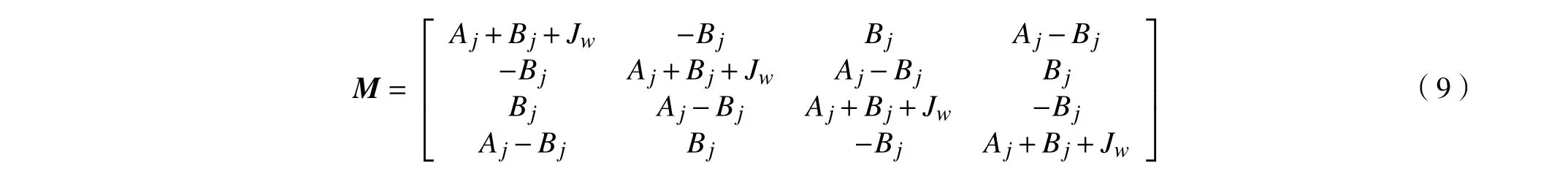
2 反步法运动学控制器设计

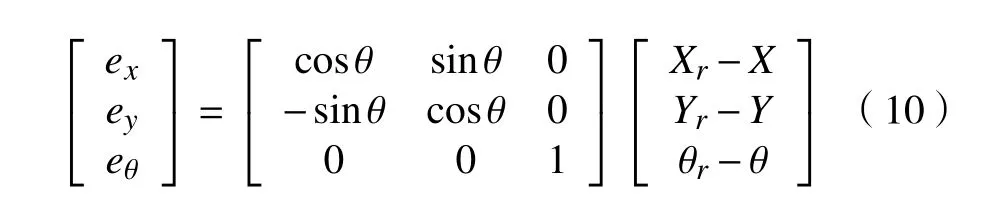
设ODMR 的参考线速度和角速度分别为 vr和ωr，则在广义坐标系中满足如下速度转换方程：对式（10）求1阶导后联立式（11）得到误差微分方程为：

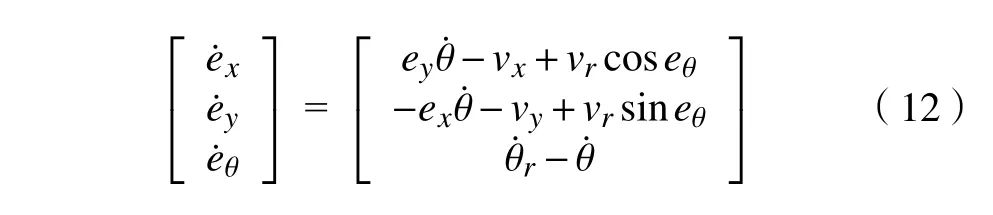
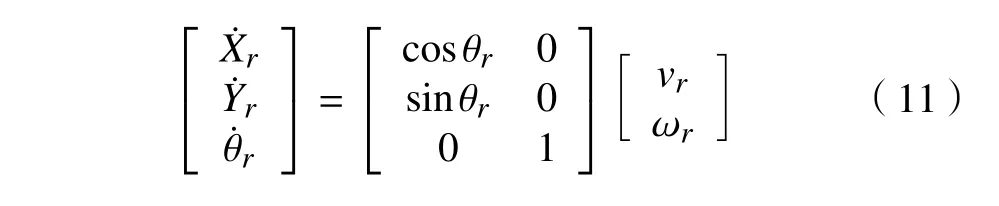
基于反步法设计思想构造李雅普诺夫函数[16]，设计如下运动学控制律：

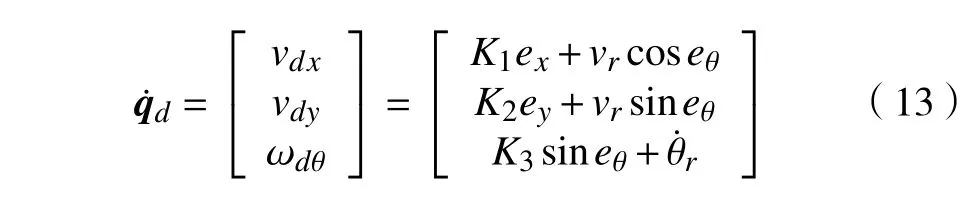
式中： K1、K2、 K3为正常数。

3 自抗扰动力学控制器设计

由于运动学控制律输出的是虚拟速度，ODMR在运动过程中受动力学参数影响更为复杂，因此基于虚拟速度为参考速度，设计动力学控制器可以实现更好的轨迹跟踪。首先设计扩张状态观测器来估计扰动值，然后设计动力学控制器并实时补偿扰动。

3.1 扩张状态观测器设计

在实际问题中会存在重心偏移、振动等不确定因素对运动性能产生影响，故观测器能否准确对未知扰动进行动态估计与实时反馈是控制器设计的关键。由式（8）建立含有不确定因素的动力学方程为

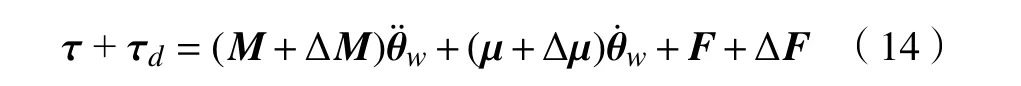
式中：ΔM 为 M的 不确定量； Δμ为μ的不确定量；ΔF 是 F的不确定量； τd为 τ 的未知输入扰动。ξ=(ΔM+Δμ+ΔF-τd)

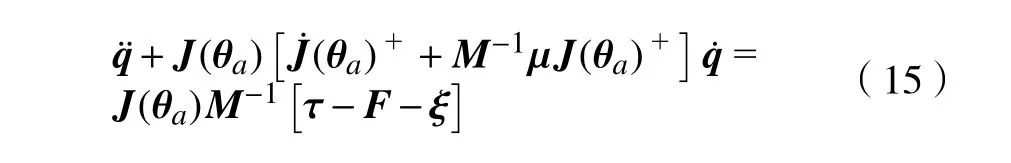
令，联立式（5）、式（14），并整理得到式中： ξ为机器人运动过程中所受不确定变化量和未知输入扰动及未建模干扰项的集总扰，且 ξ有界可导；

根据式（15），分别定义ODMR 的状态变量为x1=q ，x2=， x3=σ(t)=-J(θa)M-1ξ，因此建立系统的状态空间方程为：

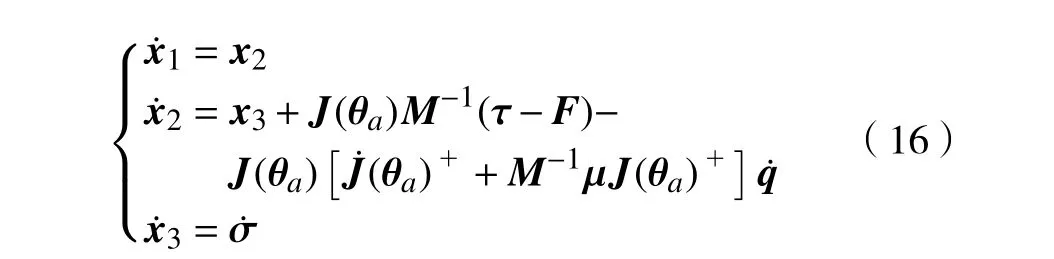
为了提高观测器的估计能力，采用滑模技术来控制观测误差，并根据误差大小设计可相互切换的线性/非线性扩张状态观测器。传统的滑模面通常是比例-微分的形式，但易引起抖振，为了削弱这一缺点，引入比例-微分-积分形式的滑模面为[17]

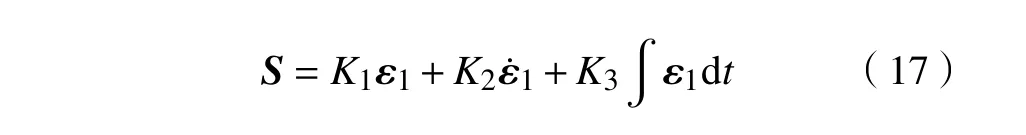
式中： ε1为位姿观测误差，定义为ε1=q-z1；zi为状态变量 xi的估计值。

同时采用幂次趋近率s˙=-β|s|αsgn s，并改写为

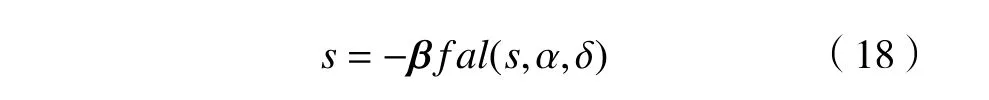
根据式（16）建立如下滑模线性/非线性切换扩张状态观测器：

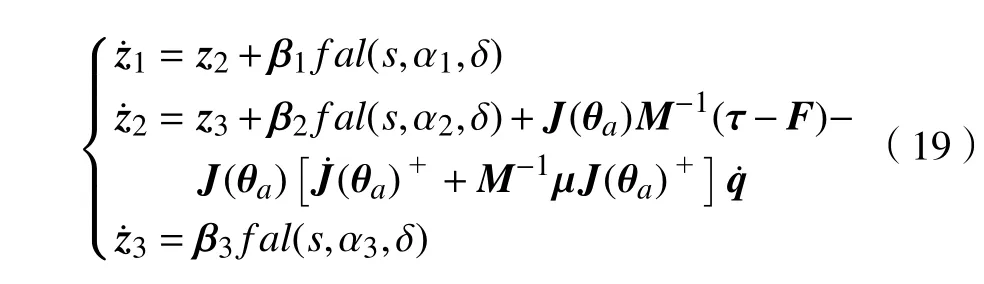
式中：ω0为观测器宽带，且ω0＞0；根据文献[18]可知：

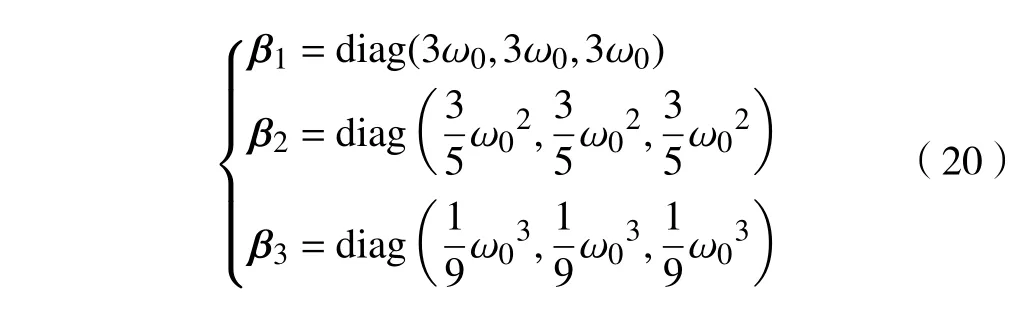
3.2 动力学控制器设计

基于无源性思想的动力学控制器是根据状态反馈来重建系统能量，并通过观测器与控制器组合来实现控制系统的误差[19]。拉式方程导出的动力学模型已直接定义了从实际控制输入 τ到 q˙的被动映射，因此改进传统无源性轨迹跟踪控制器的设计如下

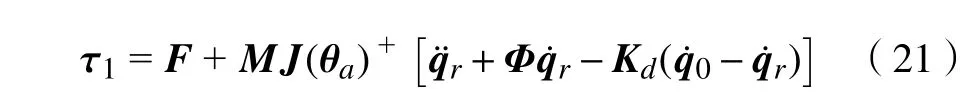
式中：Φ=J(θa)[(θa)++μM-1J(θa)+]；e 为系统控制误差，e =q-qd；和均 为辅助变量，=-Λe，=z2-Λε2，其中 Λ为 定常矩阵， Λ=diag(ωc,ωc,ωc)，且ωc＞0。

集总扰反馈补偿设计如下

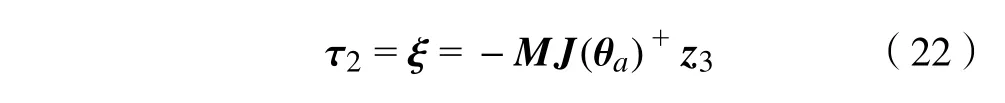
将集总扰动估计部分并入无源性控制器中作为整体来实现两者组合，由此得到最终的无源性动力学控制率为

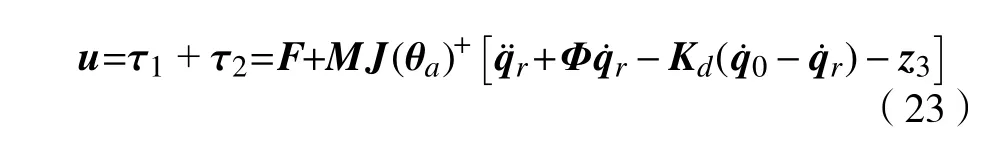
式中 Kd=diag(ωc,ωc,ωc)。

4 稳定性分析

联立式（15）与式（23）得闭环动态跟踪误差方程为

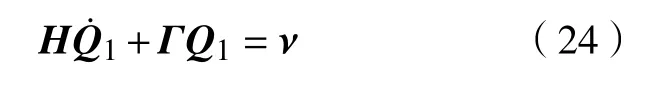
式中：Q1=；ν=H(KdQ2+ε3)，ε3为扰动观测误差值；Q2=；H=MJ(θa)+；Γ= M(θa)++M-1μJ(θa)+)。

因M 是正定对称的惯性矩阵，雅克比矩阵是q 的变换矩阵。根据文献[20]对于任意 q ，x ∈Rn满足λminM||x||2＜xTMx ≤λmaxM||x||2，其中： λmin和λmax分别是最小最大特征值。

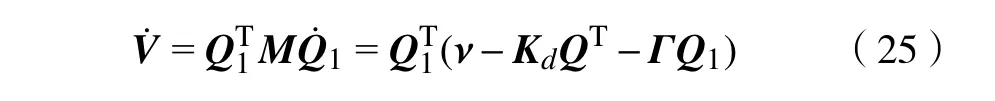
5 仿真实验

为验证上述自抗扰轨迹跟踪控制器（SADRC）的有效性与优越性，实验采用直线、圆形及双扭线作为参考轨迹并计算累积绝对误差T(exy)、T(eθ)和最大绝对误差 exymax、 eθmax来量化控制器的性能，并与传统自抗扰控制器（ADRC）作对比，仿真采样时间均设置为0.001s，模型参数与控制器参数如表1所示，最终仿真实验结果采用的量化指标为：

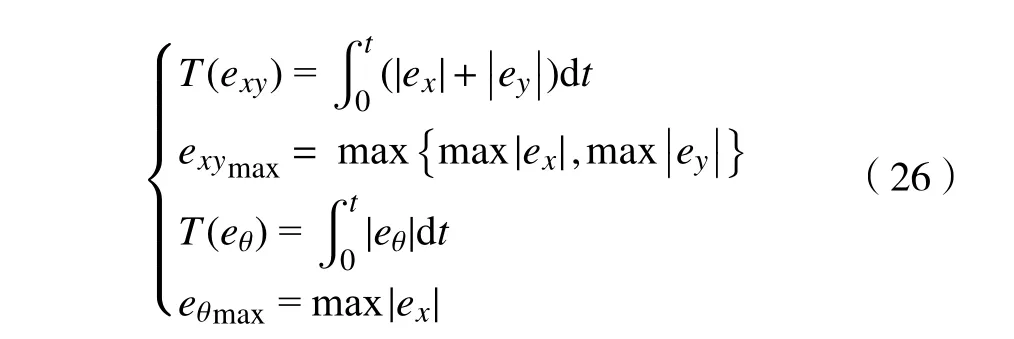
表1 ODMR 模型参数与控制器参数

实验1采用直线作为参考轨迹：Xd=0．05t，Yd=0．05t ，θd=初始位姿参考位姿将系统集总扰动同时施加在ODMR 的4个轮子上，即在10 ～20 s间在施加的总扰动同时在20～25 s施加幅值为0.1 m，频率为5 rad/s的正弦信号，实验结果如图2～ 图6所示。

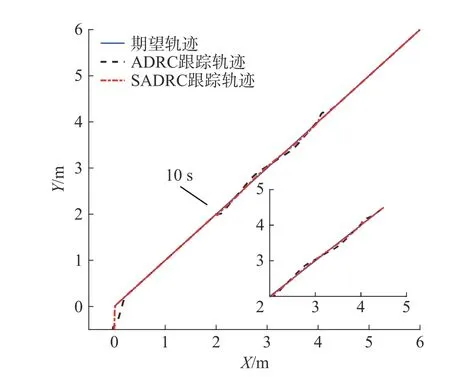
图2 直线轨迹跟踪

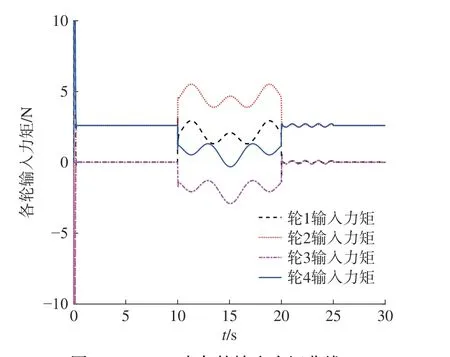
图6 SADRC中各轮输出力矩曲线

图2 表示两控制器在直线参考轨迹中的跟踪效果，其中ADRC的跟踪曲线有明显波动现象。对比图3与图4的直线跟踪误差曲线，SADRC的误差曲线在起始时刻无剧变现象，扰动期间误差曲线平滑且误差值较小，可见对扰动有抑制作用，且收敛快。而ADRC在受到干扰的起始时刻，因集总扰动的幅值或其导数变化较大，导致其系统性能急剧下降而出现较大的误差峰值，且控制欠平稳。图5中可见改进后的观测器对集总扰估计响应速度快，其估计曲线基本与实际输入扰动相拟合，观测值始终没有明显的误差，而ADRC于扰动起始时刻均存在明显误差，尤其在20 s 时刻因固定增益而导致出现峰值现象。图6中力矩曲线符合了机器人沿直线以不变角度移动时的Mecanum 轮运动特性，且受扰过程可实现实时补偿力矩。表2中的评价指标中，两控制器的eθmax相差并不大，严格来说SADRC 稍逊于ADRC，但SADRC在整个跟踪过程的T(exy)和 T(eθ)以及exymax均优于ADRC。综上，SADRC在直线跟踪过程 中的抗扰能力较强，鲁棒性更好。

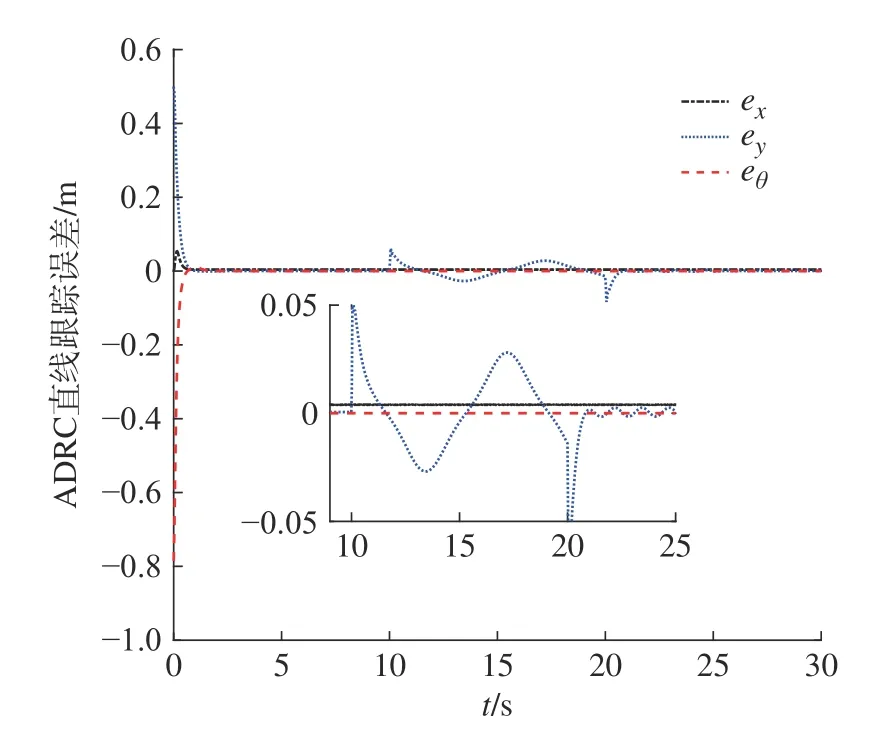
图3 ADRC直线跟踪误差曲线

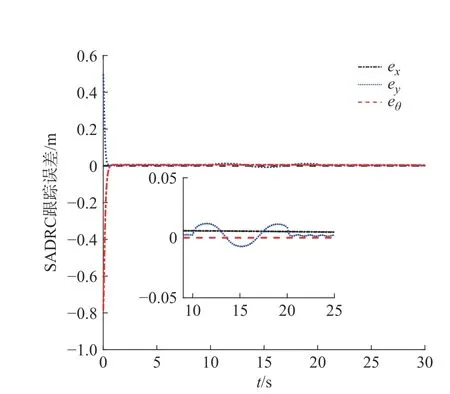
图4 SADRC 直线跟踪误差曲线

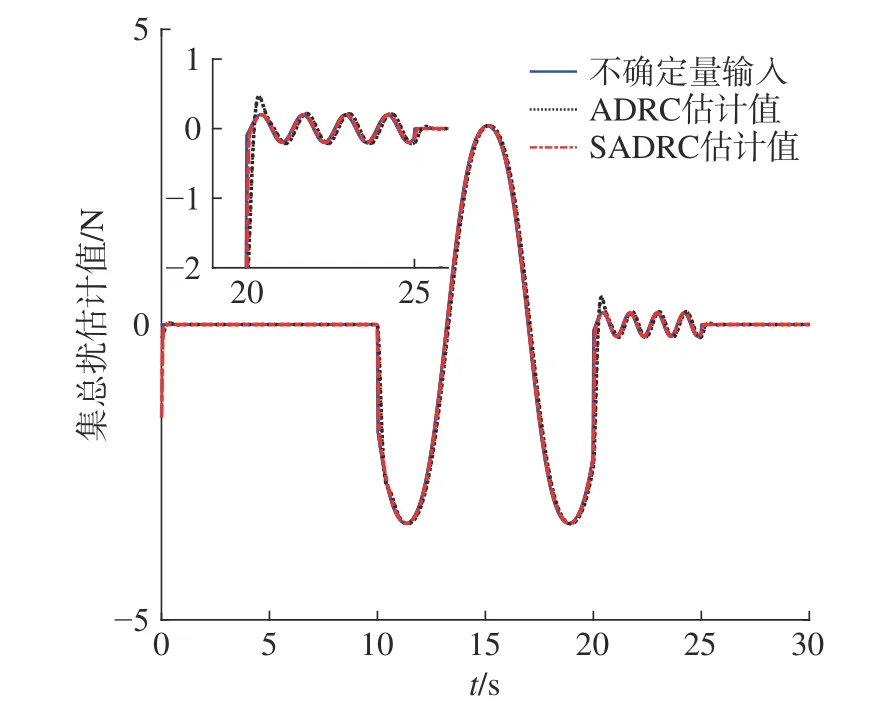
图5 集总扰估计曲线

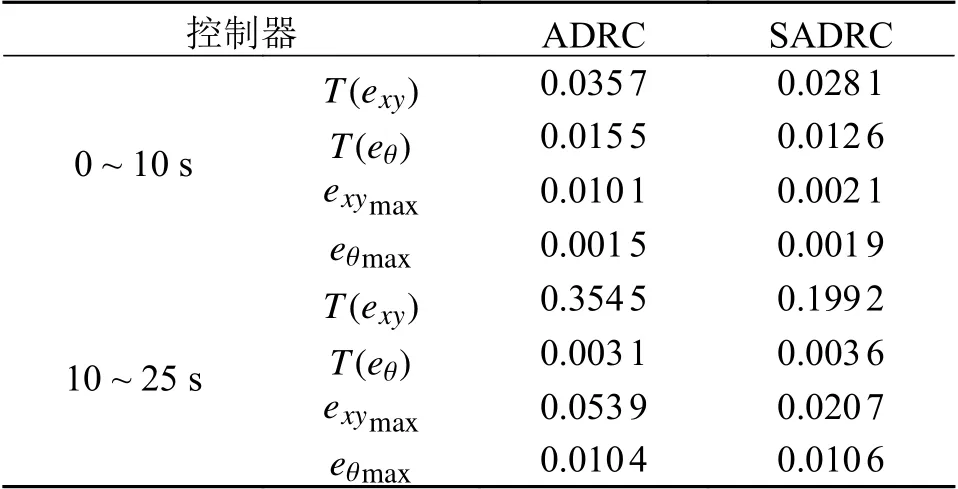
表2 直线轨迹评价指标

实验2采用圆形和双扭线作为参考轨迹，并选取双扭线实验结果进行分析。其中采用的圆形参考轨迹为双ã扭线参考轨迹为：θd=0。初始位姿均参考位姿将系统集总扰动施加在ODMR 的第一个轮子上，即在10～ 20 s间第一个轮子施加的总扰动同时在20～25 s施加幅值为0.1 m，频率为5 rad/s的正弦信号，得出的实验结果如图7～ 图12所示。

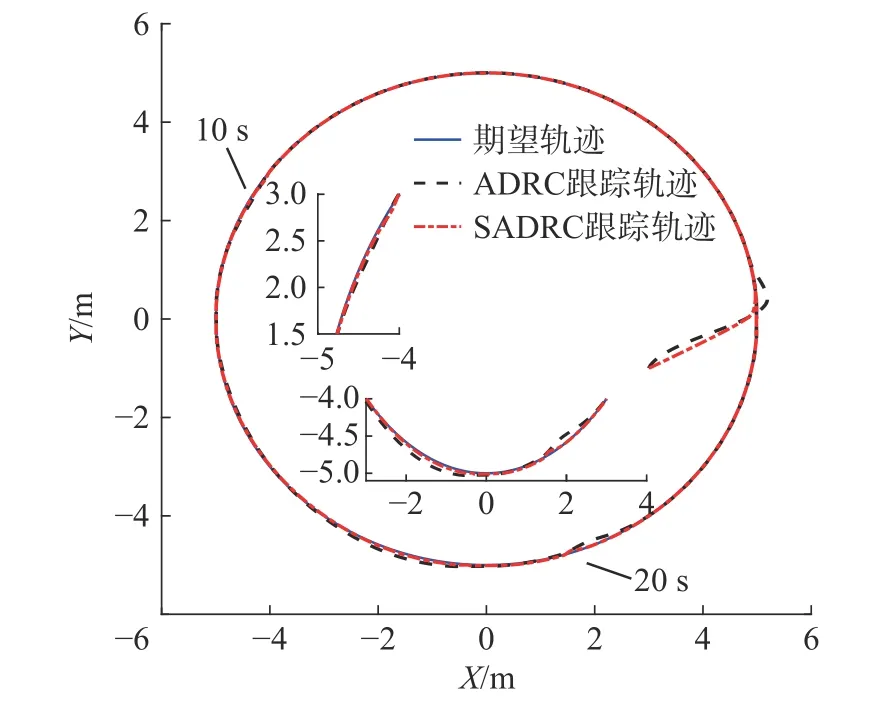
图7 圆形轨迹跟踪

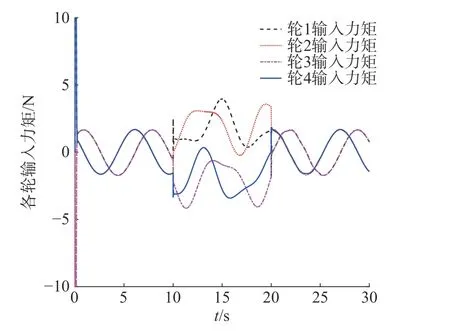
图12 SADRC中各轮输出力矩

由图7和图8看出，两控制器在受到相同扰动过程中，SADRC均无明显偏离参考轨迹的现象，可见其总体动态跟踪效果较好。图9和图10对比，ADRC的响应速度略慢，稳态误差较大，受扰动期间的横纵位姿误差曲线峰值较大且波动较为明显。相反，SADRC 收敛速度快，扰动过程的横纵误差曲线无明显震荡现象，误差峰值较小，克服了ADRC受扰过程因增益不变而引起性能急剧下降的缺点。图11中观测误差曲线说明了改进后的观测器与所设计的滑模函数结合后响应速度灵敏，估计精度高，且观测器在带宽值较小的情况下十分稳定，传统滑模控制的抖振现象不明显。对比表3中的评价指标，两控制器的eθmax仍然相差不大，SADRC在扰动跟踪过程中的T(exy)和exymax均优于ADRC。但在整个跟踪过程中，SADRC在T(eθ)上稍差于ADRC。图12中力矩曲线体现了机器人沿双扭线轨迹移动时的各轮输入虚拟力矩，因其以恒定角度进行平移而需要不断调整四轮转速，故在无扰动期间呈波形曲线，符合其运动学特性。综上，在双扭线跟踪控制中，改进后的控制器仅在角度位姿控制上欠佳，其余指标均优于传统控制器，在一定程度上抑制了误差峰值，体现了SADRC整体跟踪能力有更好的抗干扰性和鲁棒性。

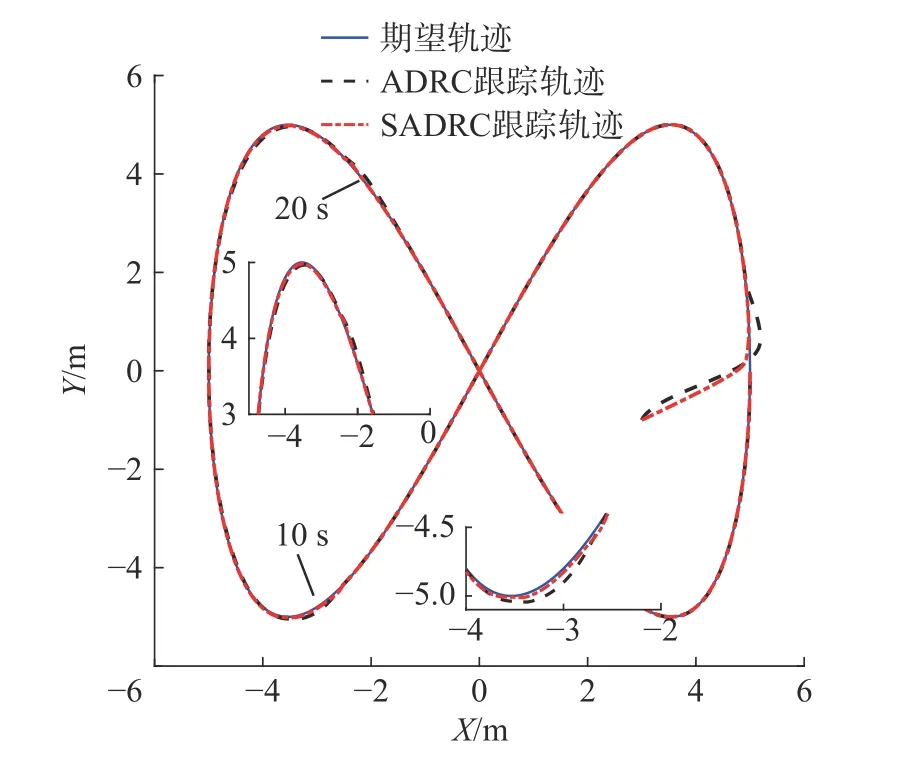
图8 双扭线轨迹跟踪

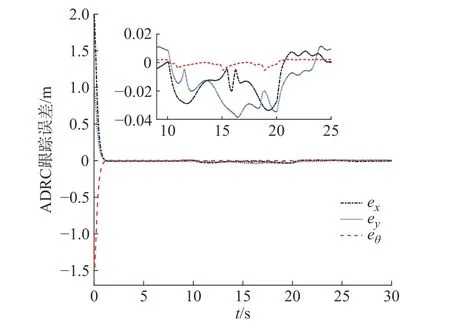
图9 ADRC双扭线跟踪误差曲线

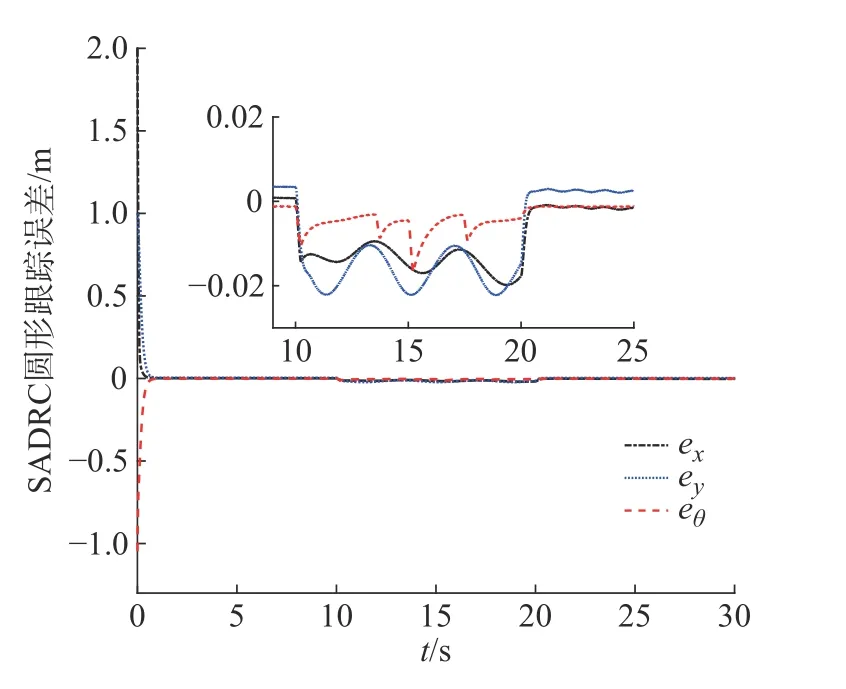
图10 SADRC双扭线跟踪误差曲线

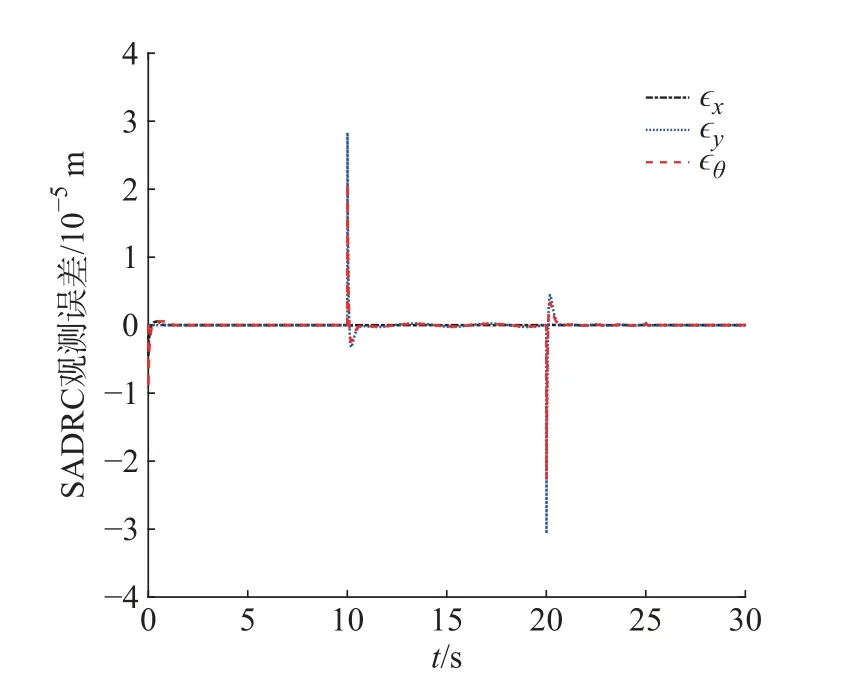
图11 SADRC双扭线位姿观测误差曲线

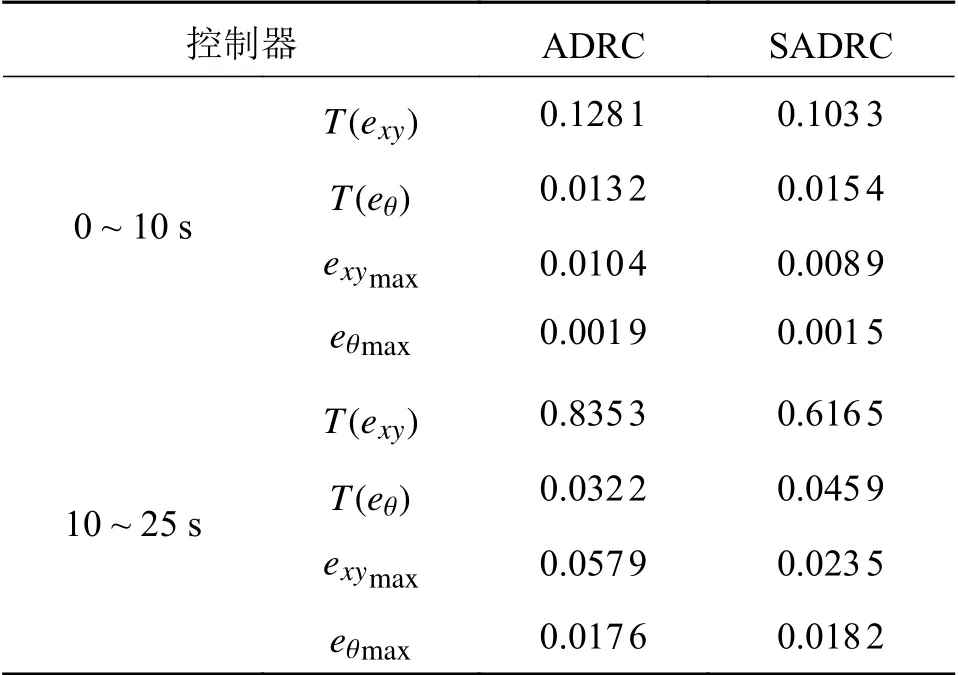
表3 双扭线轨迹评价指标

6 结论

本文针对4-Mecanum 轮全向移动机器人在实际应用中，存在负载变化导致的重心偏移，复杂路况引起的滑移、振动及其他未知输入干扰等不确定因素，基于反步法与无源性思想分别设计了运动学控制器和自抗扰动力学控制器，并通过改进扩张状态观测器对不同形式的集总扰动进行更准确的估计与补偿，仿真结果证明了本文设计的控制器在总体控制效果中有较好的鲁棒性和抗扰性。下一步工作将在全向移动机器人实验平台上对本文设计的控制器进行验证和完善。