关中地区日光温室前屋面曲线标准化设计
2022-02-13赵昱权
赵昱权
(1.西北农林科技大学水利与建筑工程学院,陕西杨凌 712100;2.西北农林科技大学旱区农业水土工程教育部重点实验室,陕西杨凌 712100)
0 引言
日光温室前(采光)屋面不仅是温室的主要的采光结构,还直接决定了其蓄热和力学承载能力等诸多因素,日光前屋面有多种形式,其形状主要有椭圆[1]、抛物线、双曲线[2]等多种类型。也有从屋面承载力的要求角度出发,得到采光屋面的类型[3]。经过国内学者对日光温室屋面的多年研究,不同形状的屋面均能保证良好的采光、蓄热与承载力要求。但是在实际日光温室工程建设中,建造者大多对设计环节不够重视,主要根据偏经验化的方法来建造,到目前为止也没有真正适合于关中地区日光温室建造的具体参数。杨凌地处陕西省关中盆地中部,位于东经108°4′,北纬34°16′之间,属大陆性季风气候。气候温和,环境条件非常利于发展设施农业。本研究在确定日光温室设施前屋面角、跨度、脊高等参数的前提下,结合以往学者的研究成果,以数学理论模型为依据,制定出适用于关中地区日光温室前采光面的曲线及参数。
1 确定日光温室基本参数
1.1 前屋面角计算
前屋面角的大小决定了温室前屋面与太阳光线所构成的入射角大小,根据前人研究,入射角的大小又影响光线的透过率[4]。当入射角为零,光线的透过率最大,但是不符合实际建设。故针对日光温室前屋面角的选择问题,前人已有大量研究,综合来看,前屋面角的计算公式为[5]:

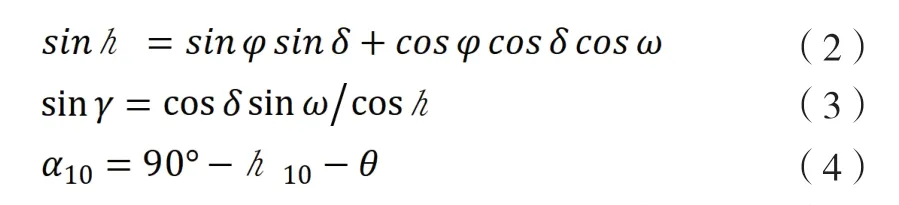
式中,α-日光温室采光面朝向正南时的最佳采光屋面角;
α10—冬至日上午10时的理想屋面角;
γ10—冬至日上午10时的太阳方位角;
h10—冬至日上午10时太阳高度角;
ω—太阳时角,取值为-30°;
δ—太阳赤纬角,咸阳地区取值为-23.094°;
θ—太阳入射角;
采光设计以冬至日为计算基准。
覆盖材料的透光率的计算公式如下[6]:
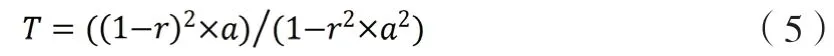
式中,γ—透明覆盖材料对太阳辐射的反射比;
α—光在玻璃内前进时穿透的比率。
根据以上公式得出日光温室玻璃的透光率以及太阳入射角的变化关系得出数据。具体结果如图1所示:太阳入射角在0°~40°范围内透光率并无太大的变化,当太阳入射角超过55°时,玻璃的透光率急剧下降。
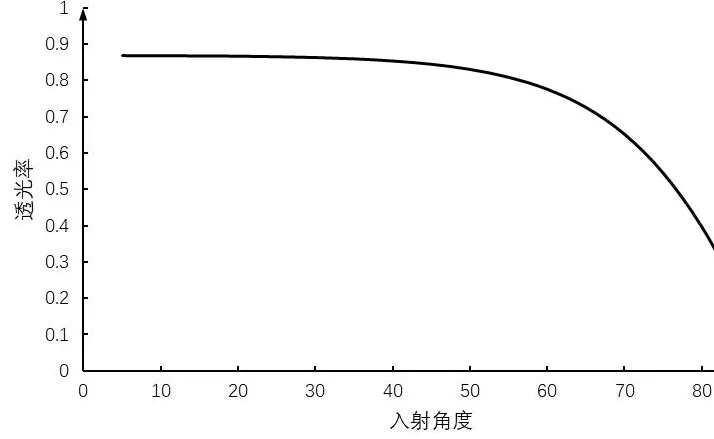
图1 太阳入射角与玻璃透光率的对比
在实际工程上,一般将薄膜透光率衰退程度的2%作为取值临界点,在图中所对应的太阳入射角为为43°。联立上式求得关中地区日光温室最佳前屋面角:
α=24.446°
根据图2,利用三角函数关系,可以计算出不同跨度对应前屋面角和脊高的表达式:
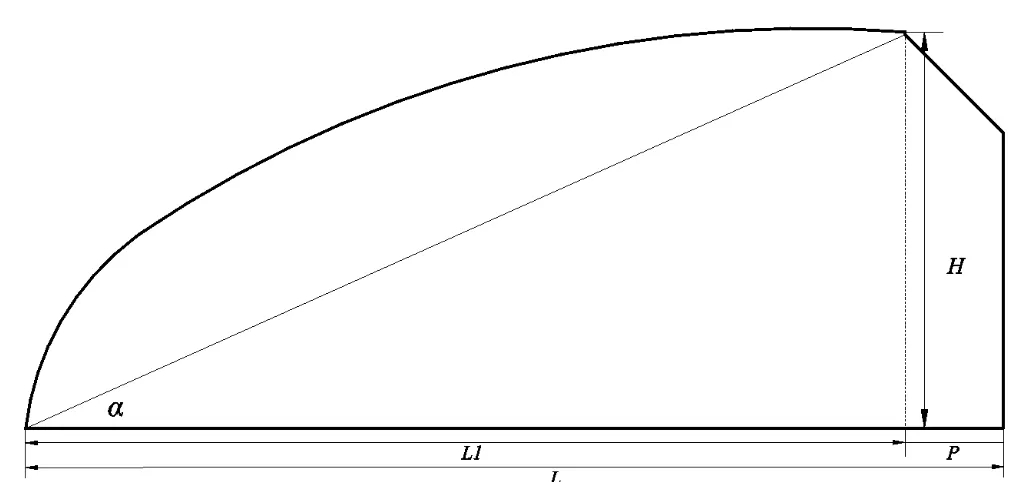
图2 日光温室总体尺寸
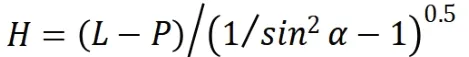
将最佳屋面角代入(6),得脊高与后屋面水平投影关系式:

1.2 后屋面水平投影与脊高
脊高在日光温室跨度和前屋面倾角确定后,即可有相应公式确定[7]。
后屋面主要作用是温室保温,后屋面面积占温室比重越大越有利于保温,同时还需考虑前屋面保证夏至日最后一排植株区域的顶层白天能接收到太阳光照射[8],根据图3,即要求保证:
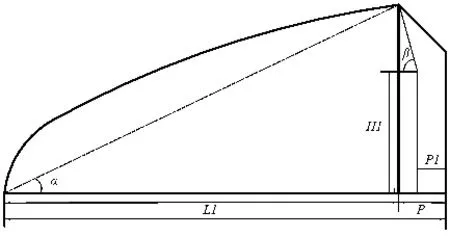
图3 最后一排作物冠层区域光照示意图
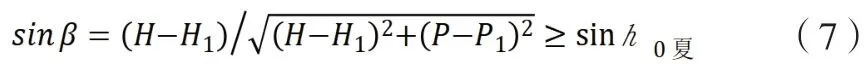
H1为一般植株高度,取2 m;P1为温室走到宽度,取0.6 m。代入公式(2-7),得到公式:

咸阳地区夏至日太阳高度角h0夏为79°,代入式(2-8),得:

联立(6)(8)两式,令日光温室跨度L=10 m,求得出后屋面投影宽度为1.006 m,脊高H=4.092 m。
按照前文得到的前屋面角、脊高、跨度以及后屋面水平投影的相互关系,设计陕西关中地区9 m,10 m,11 m三种跨度日光温室总体尺寸。相应的取值如表1,并以10 m跨度为例设计3种前屋面曲线。

表1 咸阳地区日光温室主要尺寸取值
2 建立前屋面曲线
为了方便研究采光面曲线类型,首先对当地地区目前存在的日光温室结构进行对比:当地日光温室采光面基本接近于双曲线组合形式,且多为圆弧幂函数与双圆组合为主。其次为保证日光温室离有足够的作业区域,当地地区要求温室底脚区域不能过低,在距离底脚1 m处,其屋面高度大于等于1.5 m;为方便雨雪滑落,前屋面在脊高处应有一定倾角;为使日光温室达到良好的防风效果,采光面最好采用曲线型[9],且多段曲线型采光面在数学上应满足:曲线在交汇处一阶导数相同,且光滑连续。
为保证陕西关中地区对日光温室的基本要求能够实现,现根据数学理论,基于采光要求,设计三种日光温室采光面形式,并计算各温室内太阳辐射总量。
2.1 圆弧与幂函数曲线
幂函数与圆弧屋面的设计原则是,屋面上半部采用半径为R的圆,圆心为O,下半曲线为幂函数曲线。两端曲线相交于B点,坐标为屋脊点的高度已经确定,坐标为C南底脚的坐标为A初步设计日光温室曲线,如图3所示。
对于屋脊处的上圆,在C点做满足αc≥10°的屋面切线,过C点做垂足于该切线的直线OC,连接BC两点,取垂直平分线并延长,直线OC与α垂直平分线交于O点,即为上圆的圆心O与半径R。
根据上述对圆弧的数学理论,应采用具体的数学方法确定屋面系数,圆的数学公式为:则上圆弧的各个参数计算公式为:
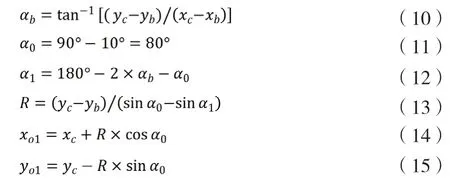
根据前述确定的日光温室脊高,跨度,以及后屋面水平投影的数值,代入上圆弧计算公式,得出其圆心坐标为(14.277,-25.836),半径为30.39 m,其参数方程为上圆曲线弧长为:8.49 m。
总弧长L1=9.524 m。
绘制出的第一种前屋面曲线如4所示。
2.2 双圆弧屋面曲线
对于上圆参数和方程不在做过多赘述。由于下圆的半径与上圆重合,下圆方程与上圆设计思路相似:连接AB做垂直平分线并延长,交于上半圆OB线上,即为下圆的圆心与半径,另外要注意的是上圆与下圆的交点B处,其左右邻域的斜率相等。具体曲线如图4所示。

图4 幂函数与圆弧曲线
上圆弧圆心坐标为(14.277,-25.836),半径为30.39 m,其参数方程为
下圆弧圆心坐标为(14.277,-25.836),半径为30.39 m,其参数方程为上下圆弧的弧长分别为:8.49 m、1.89 m,总弧长L2=10.35 m。
绘制出的第二种前屋面曲线如5所示。
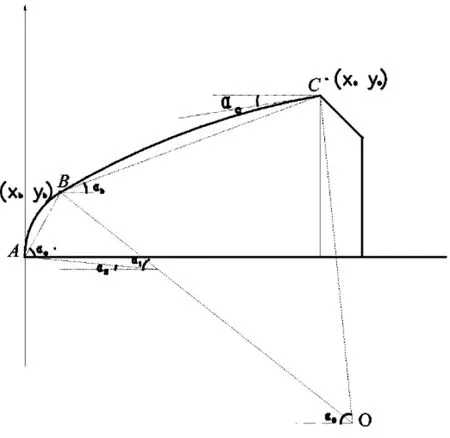
图5 双圆弧曲线
2.3 三次样条曲线
三次样条函数形式有:
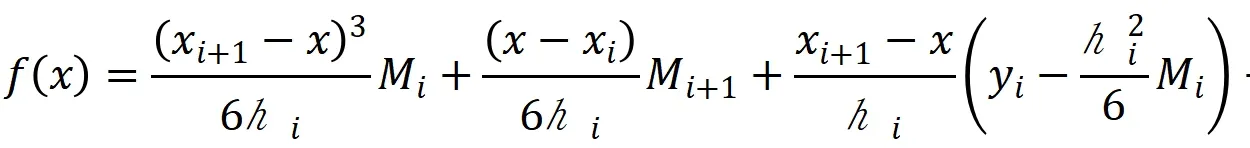
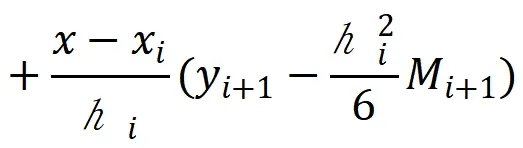
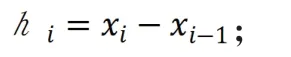
为了方便研究采光面曲线类型,对杨凌智慧园日光温室的结构进行考察,当地日光温室采光面基本为双曲线。并将所测得数据进行拟合,跨度与脊高的数值如表2所示:
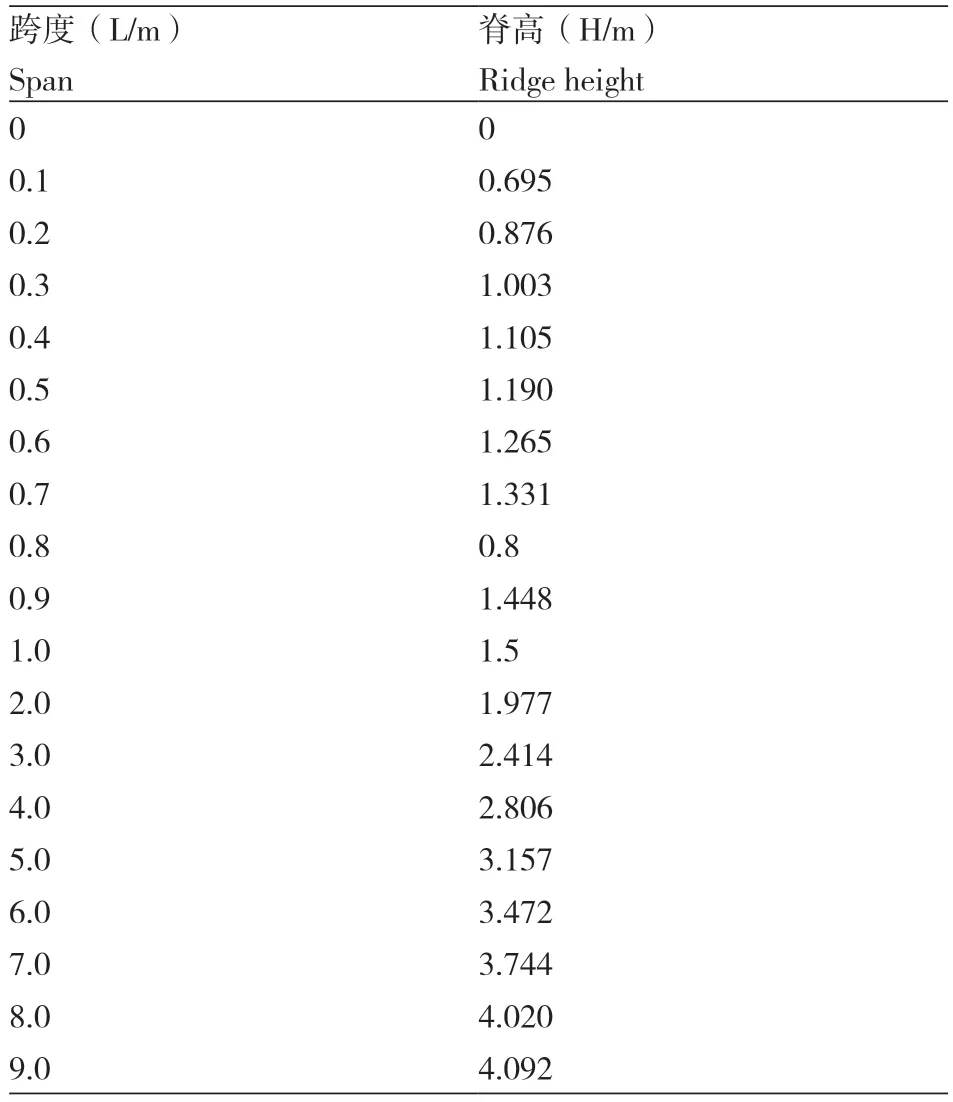
表2 不同跨度对应脊高
根据表2,求得上函数表达式为:
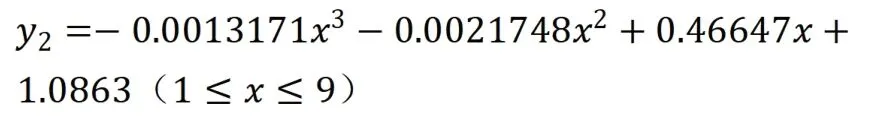
下段函数为自然对数函数:
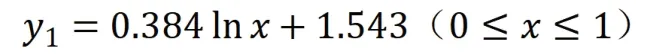
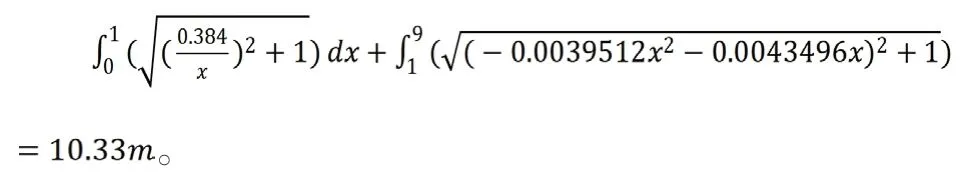
三种日光温室曲线如图6所示,在确定日光温室设施前屋面角、跨度、脊高等参数的前提下,以数学理论模型为依据,只需代入基本参数,利用数学算式,即可获得不同条件下日光温室曲线方程,利于实际施工画图,计算,以及搭建温室桁架。
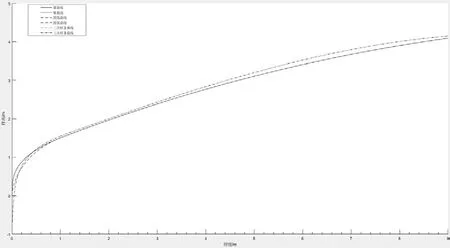
图6 三种日光温室前屋面曲线对比
3 太阳辐射计算
3.1 太阳通量辐射计算
根据太阳总辐射通量公式[10],可计算两种曲线在冬至日一天中温室内的太阳辐射量,公式为:

B为骨架间距;
L为曲线方程;
San为太阳辐射通量。
3.2 计算结果对比
对于第一种温室曲线:
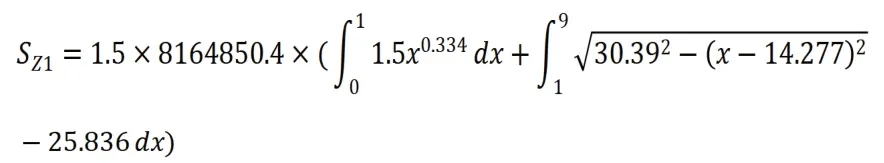
对于第二种温室曲线:
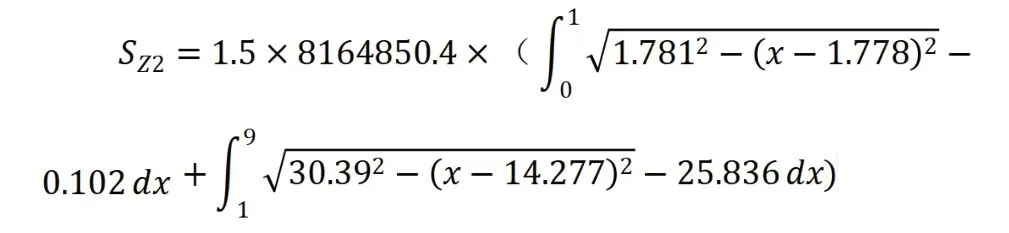
对于第三种温室曲线:

由结果可知,总弧长关系为:,太阳辐射通量关系为:。
从进光量角度来看,陕西关中地区最优的前屋面曲线为。从节省材料角度来看,陕西关中地区最优的前屋面曲线为。
4 结论
以关中杨凌地区的太阳辐射和气候特征为例,在确定温室设施前屋面角、跨度、脊高等基础参数的前提下,设计了两种温室采光面曲线,并分别对两种曲线进行太阳辐射通量的计算。得出一套咸阳地区日光温室前屋面曲线参数的设计。通过与对比北京地区历年实测日光温室内辐射量[11]的结果以及参考陕西省日光温室设计建造规范等相关资料。表明此类日光温室前屋面曲线设计的方法具有一定的参考价值和可行性。
由于决定日光温室前屋面曲线方程的取值有很多因素,本文设计结果只是针对基础参数固定的情况下进行分析,未能考虑温室整体荷载等多方面的影响。同时也需要在日后的设计中更加深入和提高。

表3 两种日光温室前屋面曲线表达式与太阳辐射通量
