微调情境，促进深度学习

王朝兵

摘要：笔者对人教版“两位数乘两位数”教学情境的文字信息进行了微调，使情境联系学生生活经验，有利于学生操作，凸显了优化思想，突出了各部分积的含义，促进了学生深度学习。

关键词：情境微调 算理 核心素养 活动经验 小学数学

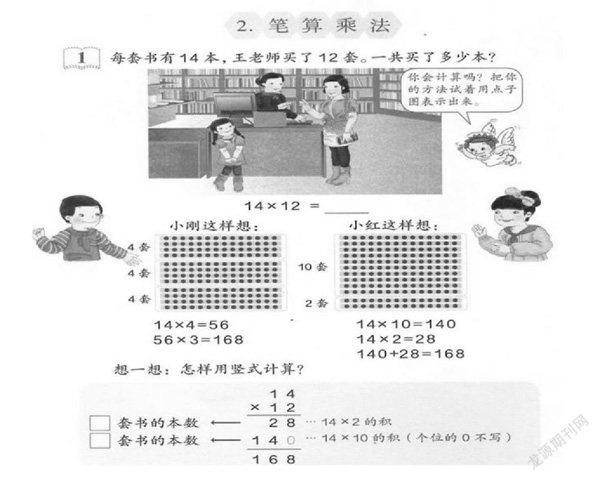
“数的运算”是小学数学的核心内容，是培养学生核心素养的重要载体。运算教学要做到明理知法。算理是数学抽象性的体现，本质是算法背后的原理，它涉及对数的概念、计数单位、数位和运算意义的理解。教学实践中，算理是课堂教学的重点也是难点。学生往往能够熟练计算，对于运算的依据却语焉不详，一脸懵懂。为帮助学生理解算理，教材在运算内容的编排上往往通过设计方块图、点子图和情境图等，提供丰富形象的图示或生活情境让学生在观察、操作和思考的基础上建构算理并能正确计算。人教版数学三年级下册为学生学习“两位数乘两位数”创设了如下情境：

学生应用已学过的计算知识，调动已有的学习经验尝试自主计算14×12，并在点子图上表示计算方法。在这个过程中学生运用旧知解决新问题，探索新知识，也培养了动手操作能力和几何直观能力;并且情境中学生借助点子图的不同操作能说出不同的口算方法，特别是情境图中右边的口算方法与竖式计算的算理是相同的，这个过程为学生理解竖式算理和正确笔算提供了丰富的活动经验。在教学实践中，三年级学生对“一套书”的理解有一些困难。一方面，是由于学生通常购书时往往只买一本或几本书，没有买成套书的生活经验;另一方面，是因为情境图中只呈现了书店购书场景，没有展现“一套书”的图示，学生缺少理解“一套书”的感性支撑。杜威说：“教学的艺术就在于能够创设恰当的情境。”理想的教学情境应是学生利用已有的知识、经验走向新知的桥梁，有利于学生主动学习，探索新知，实现新知向已知转化，建构知识体系，积累活动经验，提高思维能力，提升数学素养。因此，笔者再次教学时，对情境的文字表述进行了微调。同样的情境图，文字信息改为：“每本书14元，王老师买了12本。共付多少元？”微调情境文字，使抽象的算理形象化，促进了学生深度学习，课堂教学收到意想不到的效果。

一、微调情境 联系生活经验

“每本书14元，王老师买了12本。一共需付多少元？”直接来源于学生的生活经验，不需要理解原情境中“一套书”的概念，减少了不必要的干扰因素，有利于学生思维聚焦重难点。原情境的问题是“一共买了多少本”，解决这个问题的关系式是“每套书的本数×套数=书的总数”。虽然这个关系式是常见的数量关系式，但三年级学生多数没有买成套书的生活经验，需要结合相应情境加以想象和理解才能接受。而情境微调后的问题是“一共需付多少元”，解决此问题需应用关系式“书的单价×数的本数=书的总价”，这个关系式在学生生活中常见常用，学生有真实的购书经历和活动经验，容易用算式表示出来，集中精力重点探讨两位数乘两位数的算理算法。因此，微调情境联系了学生生活经验，有效激活了学生原有的认知，为学生探索算理引来了源头活水。

二、微调情境 利于学生操作

情境应是学生学习的助力场，是引导学生主动参与、展示思维过程的平台。学生从情境出发，解决学习疑点，攻克知识难点，自主建构知识体系。

师：每本书14元，王老师买了12本。一共需付多少元？同学们已经根据“书的单价×书的本数=书的總价”很快列出了算式14×12，你们会用竖式计算吗？

生：不会，还没有学过。

师：请思考买12本书，可以一次付钱，还可以怎么付款？请同学们独立思考后把付钱的方法和过程在点子图上圈出来，并且用算式表示出来。

学生独立完成后交流。

生1：可以一本一本付钱，付12个14元。

生2：一本一本付钱太慢。两本两本付，付6次，速度提高了一倍。14×2=28元，28×6=168元。

生3：可以四本四本付，付3次。14×4=56元，56×3=168元。

生4：可以六本六本付，付2次。14×6=84元，84×2=168元。

生5：可以先付五本付的钱，14×5=70元，再付7本付的钱，14×7=98元，70+98=168元。

生6：还可以先付2本的钱，再付10本书的钱。14×2=28元，14×10=140元，140+28=168元。

……

“还可以怎么付款？”，一石激起千层浪，学生思维充分激活。学生之所以能够想到如此多的付钱方法，源于这些方法扎根于学生的生活，在现实生活中具有极强的可操作性。学生在点子图上表示这些付钱的方法，也是轻而易举的事。把口算和生活中怎样付书钱联系起来，这为学生用竖式表达口算过程，自主建构两位数乘两位数的算理，积累了丰富的感性经验。

三、微调情境 凸显优化思想

在学生说出多种付钱方法后，接着引导学生对这些算法进行分类、比较和优化。

师：同学们真善于思考，想出了那么多付钱方法。这些付钱方法可以分为几类？

生1：可以分为连加、连乘和乘加三类。

师：以上几种付钱方法，现在请你选择一种，你会怎样选择？说说你的想法。

生2：六本六本付，两次就行了，付钱比较方便。

生3：先付10本书的钱再付2本的方法好些。因为先付10本，就是14×10，一个数乘整十数容易计算，而且不管买十几本都可以这样计算。

乘法竖式其实只是乘法计算的一种表示方式，学生往往容易掌握这种格式化的计算方法，却不理解乘法竖式背后的道理，例如：笔算两位数乘两位数为什么要从个位乘起、用十位乘得的积的末位为什么要和十位对齐等。学生在探索14×12的多种算法的过程中，感受到虽然算法不同，但是算理是相同的;又通过分类、比较、反思几种付钱方法，学生发现先付2本书的钱再付10本的方法简洁，而且具有普适性，为学生下一步用竖式表示两位数乘两位数做了铺垫，学生理解乘法竖式的算理自然也就水到渠成了。

四、微调情境 突出积的含义

计算学习的情境创设要与四则运算的意义和学生的已有经验结合起来，在实际生活中为算理搭建载体、寻找支撑，让学生能够结合四则运算的意义探索算法、理解算理。

学生会口算简单的两位数乘两位数是学习笔算两位数乘两位数的现实起点。学生口算14×12的思维过程是：14×10=140，14×2=28，140+28=168。14×2的积表示“2本书的价钱”，是竖式计算的第一步;14×10的积表示“10本书的价钱”，是竖式计算的第二步;两次乘得的积相加是竖式计算的第三步，得到12本书的价钱。“2本书的价钱”“10本书的价钱”与原情境中“2套书的本数”“10套书的本数”相比，由于学生有鲜活的现实生活经验，其中蕴含的抽象的算理找到了现实生活的表征和依托，这样学生的数学学习才是灵动而富有生命的。

总之，对教材情境中的文字进行微调使教学情境取材于学生生活实际，便于学生活动、操作和交流，为学生理解算式、建构算理找到了生活原型，也体现了算法多样化，凸显了优化思想，提高了学生的数学应用能力，提升了学生的数学素养。

责任编辑：赵潇晗