Discrete-time sliding mode control with power rate exponential reaching law of a pneumatic artificial muscle system

Quy-Thinh Dao·Trung-Kien Le Tri·Van-Anh Nguyen·Manh-Linh Nguyen

Received:16 June 2021/Revised:8 July 2022/Accepted:1 August 2022/Published online:13 October 2022

©The Author(s),under exclusive licence to South China University of Technology and Academy of Mathematics and Systems Science,Chinese Academy of Sciences 2022

Abstract This paper develops a discrete-time sliding mode controller with a power rate exponential reaching law approach to enhance the performance of a pneumatic artificial muscle system in both reaching time and chattering reduction.The proposed method dynamically adapts to the variation of the switching function,which is based on an exponential term and a power rate term of the sliding surface.Thus,the controlled system can achieve high tracking performance while still obtain chattering-free control.Moreover,the effectiveness of the proposed method is validated through multiple experimental tests,focused on a dual pneumatic artificial muscle system.Finally,experimental results show the effectiveness of the proposed approach in this paper.

Keywords Pneumatic artificial muscle·Discrete-time sliding mode control·Exponential reaching law·Chattering

Abbreviations

PAM Pneumatic artificial muscle

PID Proportional integral derivative

SISO Single input single output

DSMC Discrete-time sliding mode control

ERL Exponential reaching law

PRERL Power rate exponential reaching law

RMSE Root mean square error

1 Introduction

In modern industry,multiple actuator systems characterized by non-linearity are widely used. The pneumatic artificial muscle(PAM)system is a special one among all that stimulate human muscles by producing a contraction via internal air pressurization. The PAM consists of a rubber bladderlike tube covered by a fiber-braided shell. As the tube is inflated, the PAM is contracted. The more tension is created, the greater force is produced. PAM systems bring many advantages of good flexibility with cylinder shape,high power-to-weight ratio, low cost, ease of maintenance,cleanliness,etc.Therefore,mostly used in manipulators[1–3], rehabilitation robotics [4,5], medical devices [6], and many others [7,8]. However, it is challenging to obtain good tracking performance due to strong non-linearity,high hysteresis behavior, and the inaccuracy of the PAM mathematical model. Therefore, various control strategies have been proposed to overcome these problems in controlling the PAM-driven system.An advanced nonlinear PID-based controller is introduced in [9] for positioning control problem and hysteresis compensation. In [10], the authors implemented an inverse fuzzy model to PID controller so as to achieve good angle output performance of a PAM robot arm. Cascade position control PID-based controllers using hysteresis model such as modified Prandtl–Ishlinskii model,Maxwell-slip model are designed to compensate the nonlinearity in[11–13].These enhanced PID control methods have been widely used yet shown their drawback in the lack of robustness against hysteresis effect and high nonlinearity of PAMs.

It has been acknowledged that sliding mode control(SMC) is an effective robust control strategy in the presence of uncertainties and disturbances of pneumatic actuators like PAMs [14–19]. Nevertheless, with the recent development of digital controllers in the data-sampled system, the essentiality in discrete-time sliding mode (DSMC) design is inevitable. It is noteworthy that the control input of discrete-type SMC is updated at the sampling instant only and kept constant during the sampling period. For many years, numerous works of DSMC-based have been carried out in the literature on different kinds of systems,including equivalent control approach[20,21]and reaching-law-based method [22–25]. As the chattering phenomenon is a major obstacle in the application of DSMC,specified in pneumatic artificial muscle actuator, this paper is then concentrated on the reaching-law based control strategy which considers effective against chattering problem.It is worthwhile to note that there always exists a trade-off between chattering alleviation and robustness as well as convergence rate.Therefore,the need for a reaching-law-based approach applied in a PAM-driven system that can alleviate the chattering effect while maintaining fast reaching speed and robustness is evident.

To deal with the aforementioned problems,this paper proposes a discrete-time sliding mode controller(DSMC)based on a novel power rate exponential reaching law(PRERL)for the PAM-driven system.The exponential term was first introduced for continuous-time approach in [26], and had been applied in a variety of researches for chattering elimination but rarely employed on discrete control design.Combining with the well-known power rate reaching law[27],the proposed controller can thus perform smooth control with its chattering alleviation property and still significantly improve reaching speed with satisfactory tracking accuracy.The novelty of this work are summarized as follows:

• A discrete-time reaching-law-based sliding mode controller is established to enhance the control performance as well as chattering alleviation for a dual pneumatic artificial muscle system.

• The proposed reaching law combines an exponential term with the power rate reaching law, and is newly formulated in the discrete-time domain for digital implementation purposes.The stability along with finite steps convergence of the designed controller are theoretically analyzed by Lyapunov theory on the linear system.

• Experiment results with various scenarios such as low and high frequency,different tracking wave signals,load as external disturbance,illustrate advantages of the proposed method compared to some others in controlling PAMs.

Fig.1 Experiment platform of the PAM-based antagonistic configuration

Theremainsofthispaperareorganizedasfollows.Section 2 presents experimental setup equipment and mathematical model of the PAM system.In Sect.3,the design procedure of DSMC with PRERL-based is introduced.The experimental results and further investigations are then carried out in Sect.4.Finally,conclusions are given in Sect.5.

2 Problem statement

2.1 Materials and system structure

Thepneumaticexperimentalplatformhasbeenestablishedas presented in Fig.1 and its schematic diagram is demonstrated in Fig. 2. The structure comprises a pair pneumatic artificial muscle actuators(self-made)connected in antagonistic configuration, with 23×10−3(m) of diameter, 40×10−2(m) of nominal length. The internal pressure of PAMs is regulated through a proportional valve (SMC, ITV-2030-212S-X26), and produces rotational motion of the pulley wheel, which is measured by an angular displacement sensor (WDD35D8T). The control setup for the system is implemented using myRIO-1900 embedded controller from National Instrument,which processes the collected data from the angle potentiometer and applies the control signal to proportional valves.The whole experimental process is interfaced and monitored through LabView software.

2.2 System modeling

Considering the antagonistic configuration of system structure shown in Fig.2,which simplifies the motion control to only one variable, internal pressures of two PAMs can be described as

whereP0represents the initial pressure of PAM, which is fixed throughout the process, andΔPis the pressure difference. It should be emphasized that control voltages of

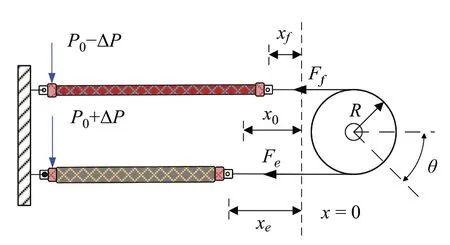
Fig.2 The structure schematic of the antagonistic PAMs system

Table 1 Model parameters

proportional valves regulating PAMs are designed as

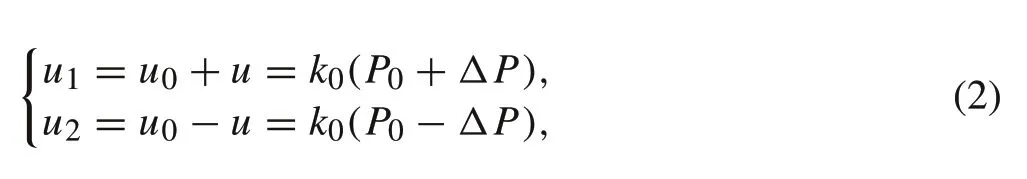
whereu0is the preloaded voltage,k0is the proportional coefficient of the output pressure for PAMs and the control voltage,uis used as a manipulated variable.Therefore,the voltageuis the control input of the closed-loop system that manipulating PAMs to create contraction, which deflects joint angleθ,and then the signal of deflection angle is transmitted back through a sensor.As a result,a pair of pneumatic artificial muscles in antagonistic configuration can be described as a single input single output (SISO) system. In this case, the control voltageuof two proportional valves would be the only input variable and output would be the measured joint angleθ.For such a motion control system,a linear model can be chosen to describe the behavior of the system with acceptable modeling error.The remaining modeling error can be regarded as a lump disturbance,and then is handled by the controller. In our research, based on the input/output data and several experiments, a discrete-time second-order linear model with perturbation is employed as the system model[28]:

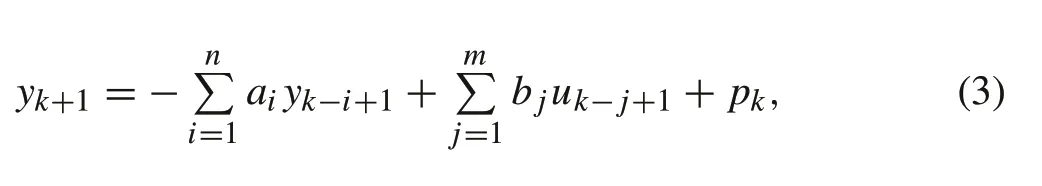
whereukis the control signal of input voltageu,ykis the angle deflection,pkrepresents the unknown uncertainties and disturbances,aiandb jare model parameters(withb j/=0),n=m= 2 are orders of the model.It can be observed from the identification result shown in Fig.3 that the chosen second-order system can effectively describe the antagonistic PAMs system with acceptable error.Specific values of model parameters are listed in Table 1.

3 Design of the control strategy

Inthispaper,theDSMCwithpowerrateexponentialreaching law is introduced for the PAM system to guarantee chattering free control and fast reaching speed without affecting the accuracy in tracking performance. The schematic diagram of the designed control algorithm is shown in Fig. 4. The proposed reaching law is based on the conventional power rate strategy combined with an exponential term,which is a modification of the constant reaching law.

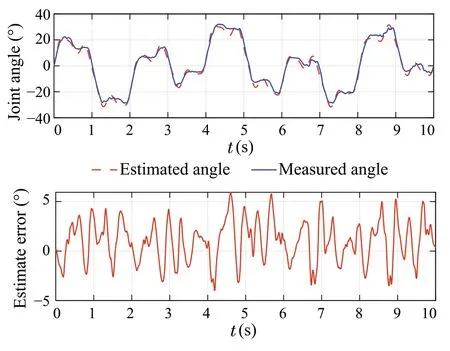
Fig.3 Identification result with a time-varying sine wave as input

3.1 Sliding surface design

Considering the selected sliding surface as

whereekis the tracking error defined asek=−ykwith the desired trajectory,andλis a strict positive constant.Taking increment from(4),one obtains

which is rewritten as

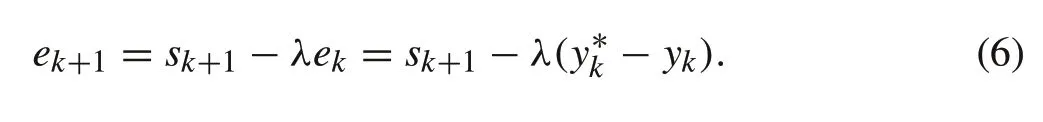
Based on the SISO model of the PAMs system chosen in(3), the one-step-ahead tracking error can be expressed as follows:

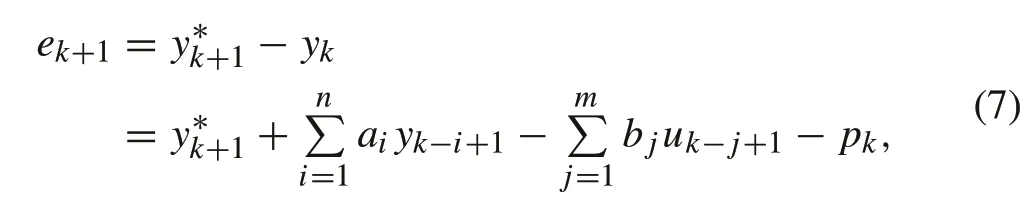
where+1is the one-step forward of the desired trajectory.As reference trajectory is predetermined in control practice,+1is assumed to be known.Substituting the tracking error in(6)into(7),one obtains

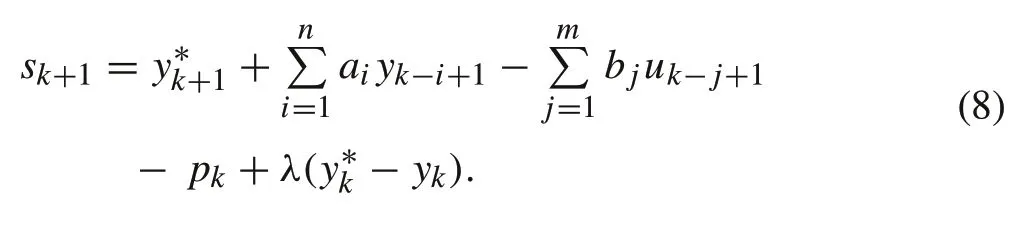
Assumption 1The generalized disturbancepkis bounded and smooth as the sampling timeTs= 5ms is relatively small,sopkis proved to possess a lemma as follows[29].

Lemma 1pk= O(Ts),pk−pk−1= O(T2s),and pk−2pk−1+pk−2= O(T3s),whereO(Ts)is the magnitude in the order of T.

Due to the fact that the disturbancepkis fairly intricate to calculate in general,thus letting the disturbancepkbe simply estimated by its decrement value as

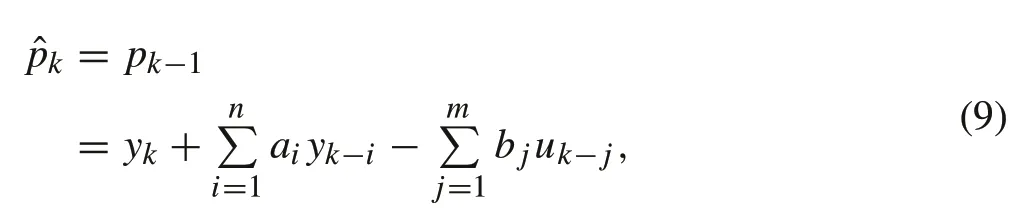
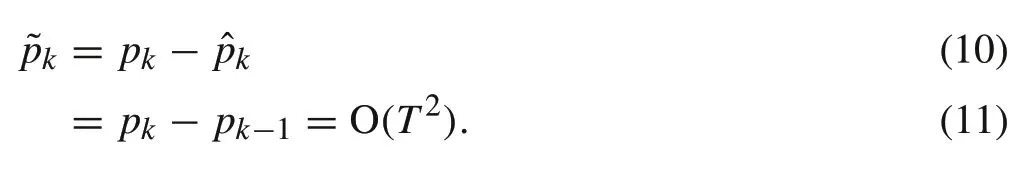
Substituting(10)into the expression of the sliding manifold in(8),it follows that

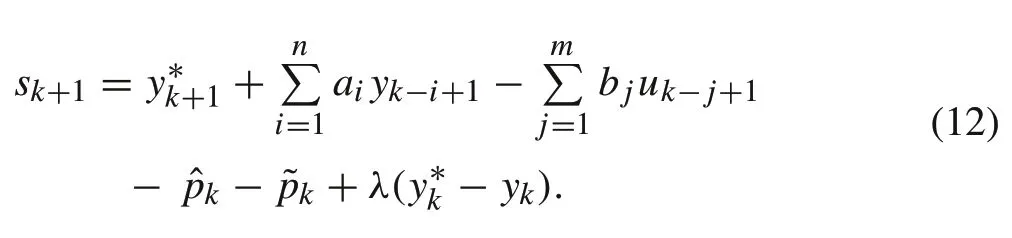
3.2 Discrete-time power rate exponential reaching law

To the extent of achieving chattering reduction, fast convergence speed and robustness simultaneously, the discrete reaching law proposed in this work is given by

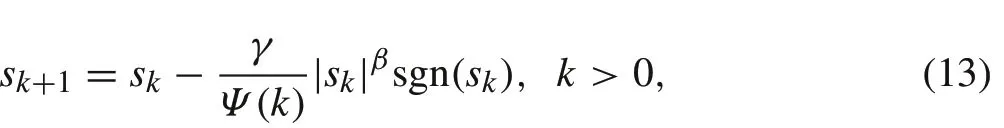
where

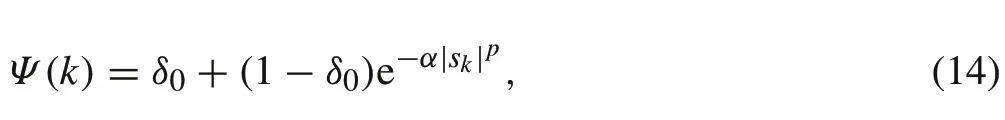
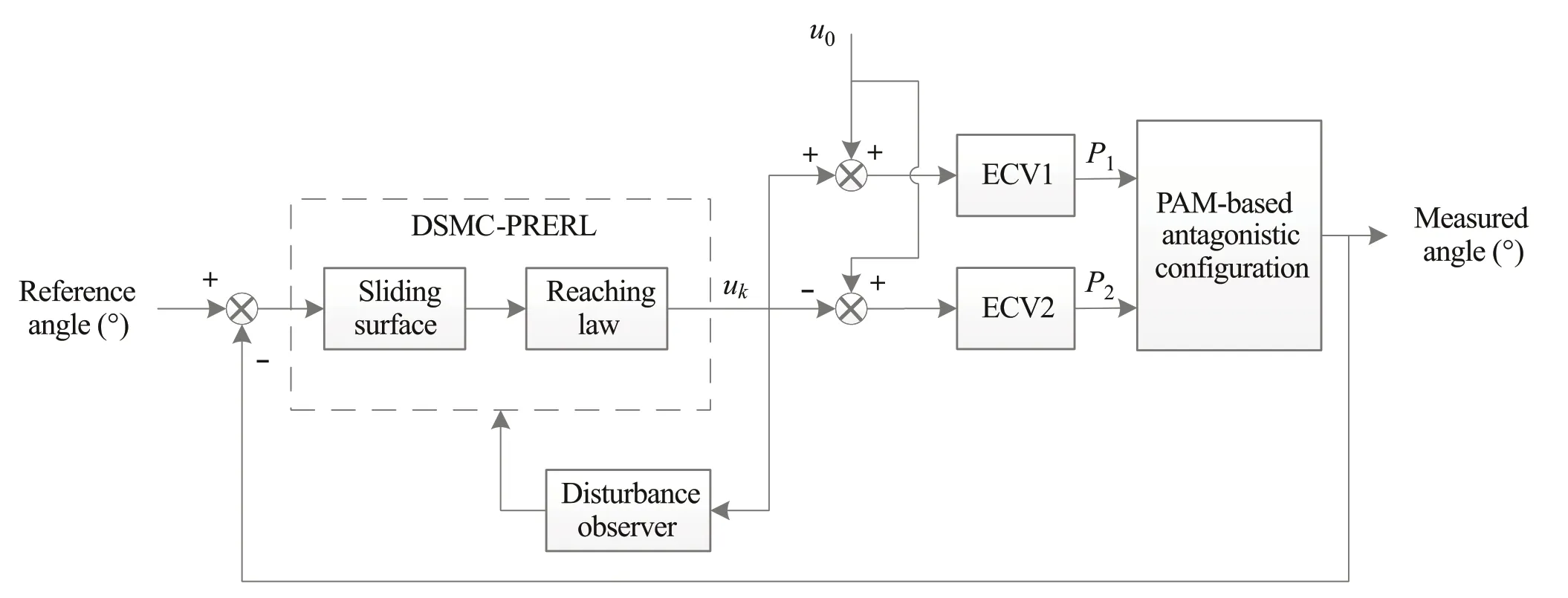
Fig.4 Block diagram of the system controller

in whichδ0,α, andγare strictly positive constants andδ0is less than one, andpis a strictly positive integer. This exponential term allows the controller to dynamically adapt to the variations of the switching function by letting the gain to vary betweenγandγ/δ0, thus reducing the chattering phenomenon. Combining with the power rate method, the proposed controller is greatly enhanced by the property of chattering alleviation as well as having the ability to improve the reaching speed compared to either the ERL-based only approach or the conventional one.

Remark 1Ifδ0andβare chosen to be equal to one and zero,respectively, the designed controller becomes the DSMC with constant rate reaching law. In other words, the conventional reaching law is a peculiar case of the proposed approach.

Then the proposed control signal is found from the reaching law by substituting sliding variablesk+1from(13)into(8),and further solving forukwhich leads to

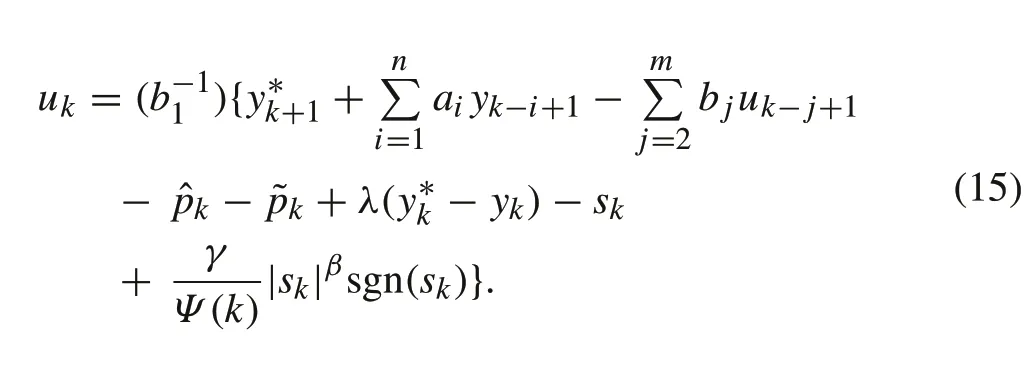
According to (11), the disturbance estimation erroris bounded and rather small in practical applications that is negligible.Hence,the feasible final form of control signalukin the absence ofcan be rewritten as

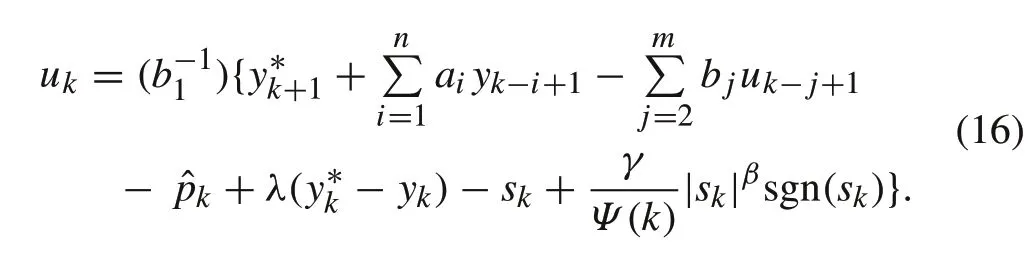
3.3 Stability analysis

In this section,the behavior of the sliding function as shown in the proposed reaching law(13)will be proven.

Lemma 2Let a positive function Φ(β)be defined as

in which1＜Φ(β)＜2if0＜β＜1[30].

Theorem 1For the discrete-time SISO system(3)along with the sliding surface(4)and the controller(16),it is ensured that the sliding variable sk will enter the region Ω in finite time,which is defined as

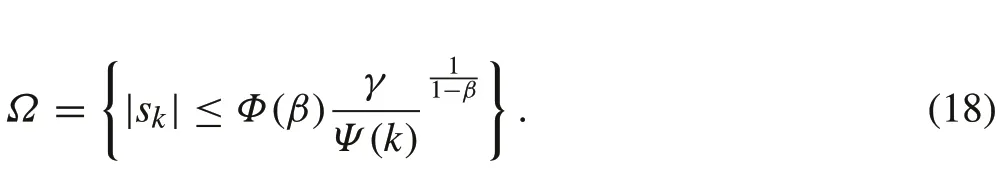
ProofChoosing Lyapunov functionVk=(sk)2and from(13),one obtains

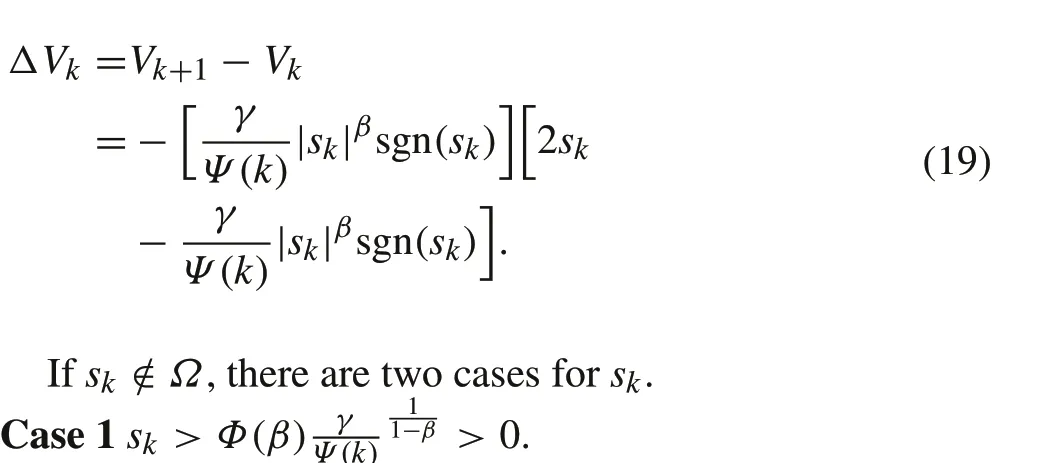
In this case,it can be derived that

which yields

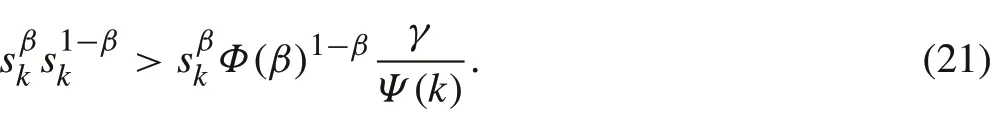
SinceΦ(β)1−β>1,the following deduction can be held:

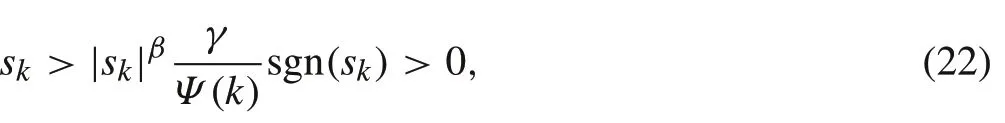
which implies

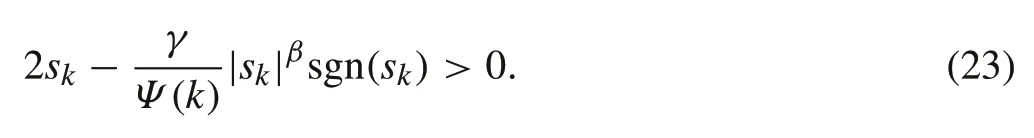
Thus,in view of(19),(22)and(23),it follows that

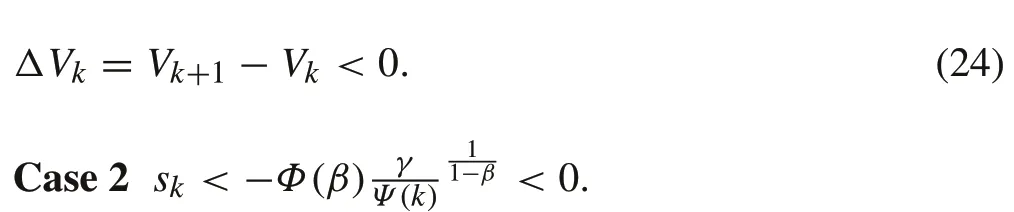
With a similar analysis,one can deduce thatΔVk＜0 still holds.

Hence,theskwill enter into the domainΩin finite steps.This ends the proof. ■

Lemma 3Given function Φ(β)as in(17),if0＜β＜ 1,then θΦ(β)−θβΦ(β)β+Φ(β)−1 ≥0for any θ∈[0,1].

ProofDefinef(θ)=θΦ(β)−θβΦ(β)β+Φ(β)−1.

First, since Lemma 2 implies 1＜Φ(β)＜ 2 if 0＜β＜ 1, we can easily deduce thatf(0) =Φ(β)−1> 0 andΦ(β)−Φ(β)β> 0,which also holdsf(1) =Φ(β)−Φ(β)β+Φ(β)−1>0.

Second,by solving ˙f(θ)=0 to find the critical points off(θ),we have

Theorem 2Once sk enters the region Ω,it cannot escape from it.

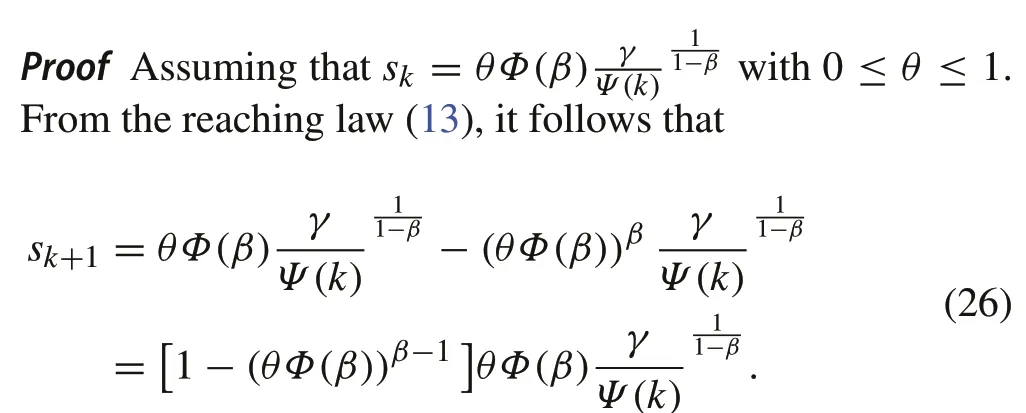
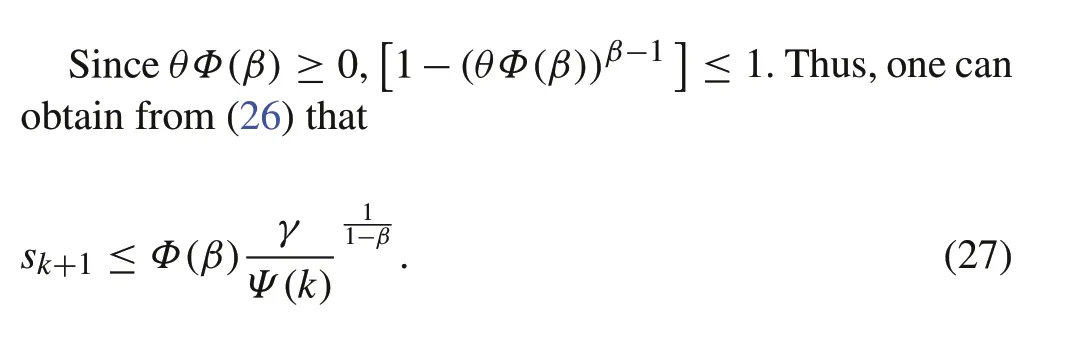
On the other hand,reviewing(26)gives

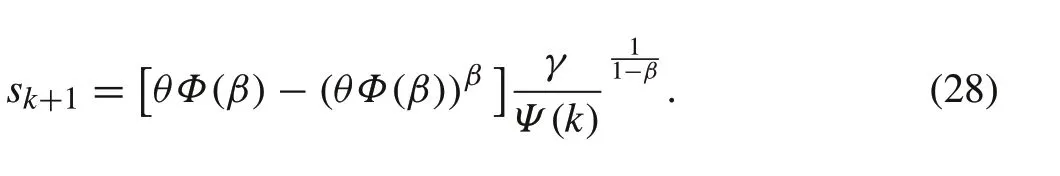
Taken 0＜β＜ 1 into account, ifθΦ(β) ≥1, thenθΦ(β)−(θΦ(β))β> 0. Also if 0 ≤θΦ(β) ≤1, then it can be derived from Lemma 3 thatθΦ(β)−θβΦ(β)β≥1 −Φ(β)≥−Φ(β).Therefore,one can conclude with 0 ≤θ≤1 that

Remark 2While the condition 0＜β＜ 1 exists as in the power rate method,a high value ofβcan result in the absence of sliding mode motion. This could ensure fast reaching to the equilibrium point but directly affect the robustness of the controlled system.Hence,βis advised to be selected within 0＜β＜0.5 as proposed in[31].

4 Experimental results

In this section,the effectiveness of the proposed controller is verified through a series of experiments with different trajectories.The employed experimental setup has been introduced in Sect. 2 as shown in Fig. 1. The sampling timeTsof the discrete-time control system is set to be 5ms.The control algorithm is developed with LabVIEW/MyRIO Toolkit and downloaded to NI MyRIO-1900 embedded controller.Furthermore, the proposed control approach is compared with a conventional discrete-time sliding mode controller(DSMC)and the one with exponential reaching law in terms of performances under the same operating conditions.Model parameters for PAMs system are shown in Table 1.The control parameters of the proposed PRERL are fine-tuned by trial and listed in Table 2. Common parameters of the two being compared are selected the same as the PRERL.

Table 2 Parameters of the PRERL controller

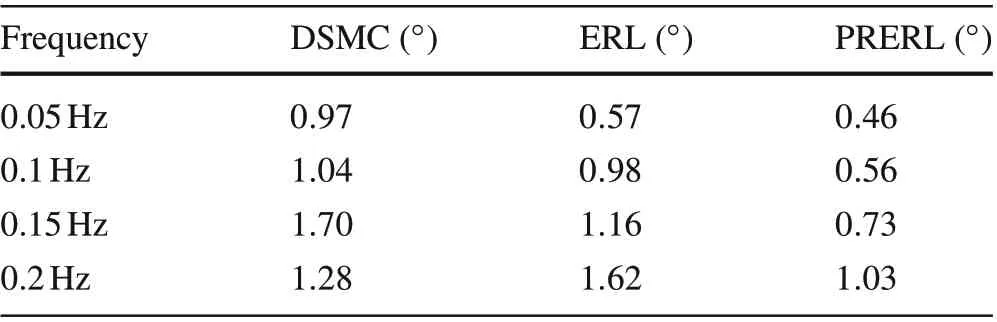
Table 3 RMSE of comparative controllers with regard to lowfrequency sinusoidal tracking experiment

4.1 Tracking low-frequencies sinusoidal trajectories

In this following part, the reference trajectories are given as sinusoidal signals with an amplitude of 20◦and frequencies ranging from 0.05 to 0.2Hz.Representative comparison results of the DSMC,ERL,and proposed controller PRERL are shown in Fig.5.It can be observed that the conventional DSMC controller leads to a serious chattering phenomenon,and also gives the worst performance with an unacceptable range of tracking error at about±5◦.The chattering behavior is partly weakened by the exponential term in the ERL controller so that its tracking performance can achieve good precision with less than 2◦of error in steady state. Despite the fact that both ERL and PRERL have much fewer control chatters as the advantage of exponential term, only the proposed approach with power rate term can achieve far better smooth control with almost chattering free operation and also greatly handle the overshoot problem in transient state.To give a quantitative analysis, the root mean square error(RMSE)of the three controllers,which is defined as follows,are summarized in Table 3.

whereNis the total number of samples.

4.2 Tracking high-frequency sinusoidal trajectories

To further investigate the effectiveness of the proposed control algorithm, three different controllers are put to the test with tracking various sinusoidal reference signals with 20◦in amplitude and frequencies of 0.5Hz,0.8Hz,and 1Hz.The tracking performance results along with tracking errors and control signals are typified in Fig. 6. It can be found that the DSMC and the ERL are strongly affected by the hysteresis effect resulted in upraising of the tracking error. On the contrary,even with the extreme input frequency of 1Hz under-tested,the proposed PRERL still can give precise trajectory tracking with less than 1.49◦of maximum tracking error in steady-state. Furthermore, the designed controller provides excellent chattering alleviation in the control signal as well as fast response speed. Therefore, the superior performance of the proposed PRERL is evidenced by the experimental results.The detailed RMSEs of the three controllers are provided in Table 4.

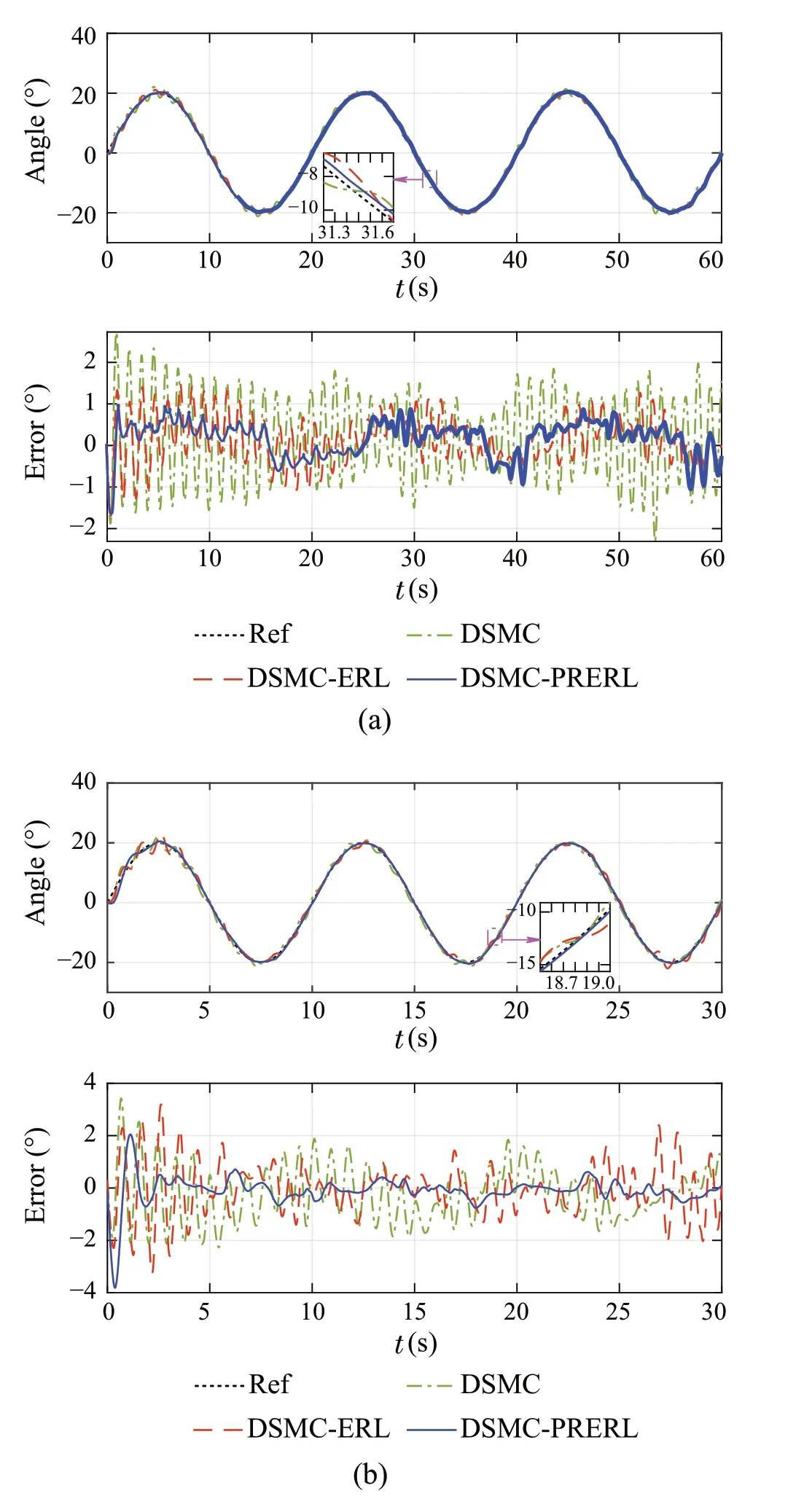
Fig.5 Experiment results for tracking low-frequency sinusoidal trajectory.a 0.05Hz,b 0.1Hz

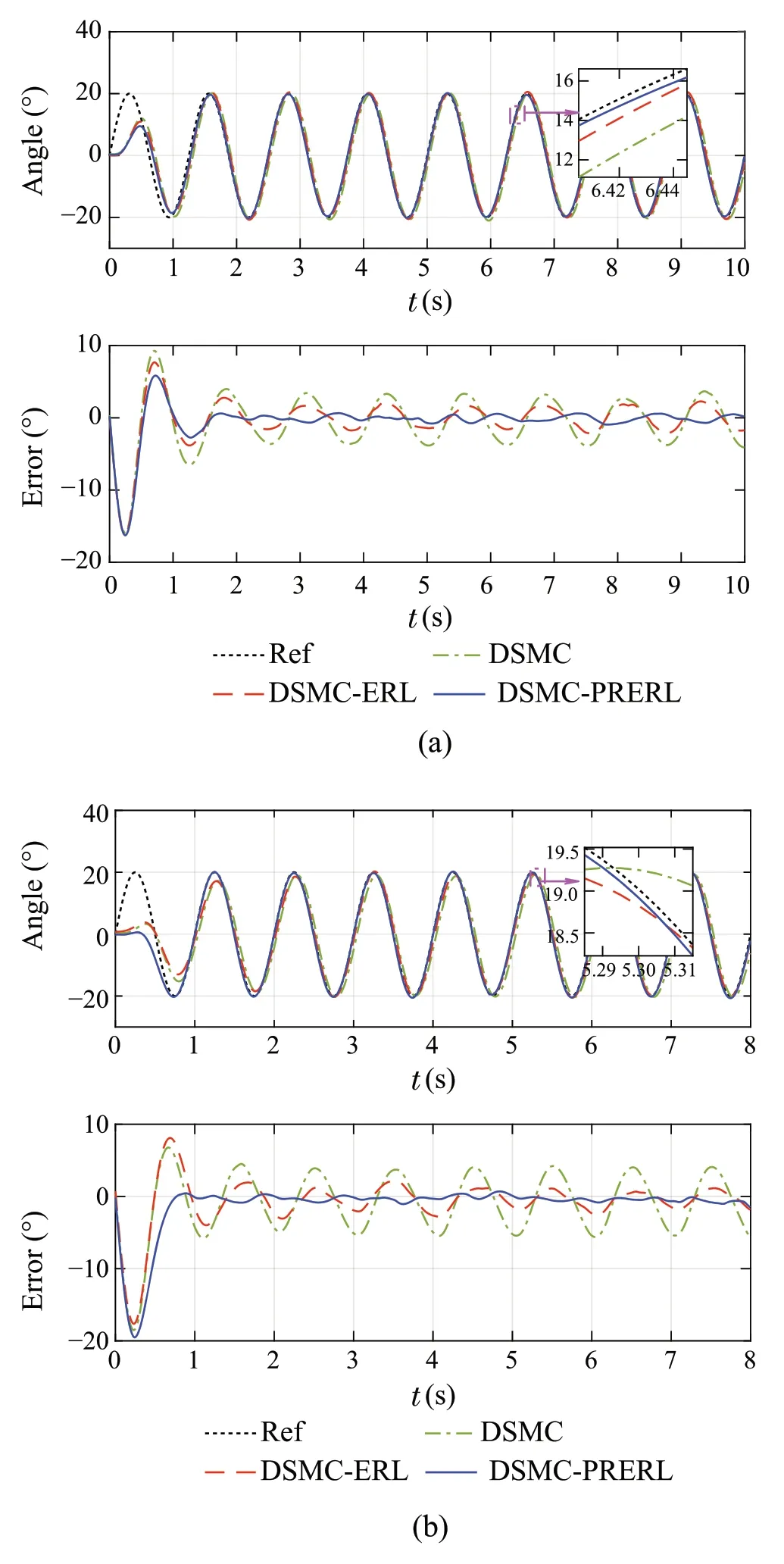
Fig.6 Experiment results for tracking high-frequency sinusoidal trajectory.a 0.8Hz,b 1.0Hz

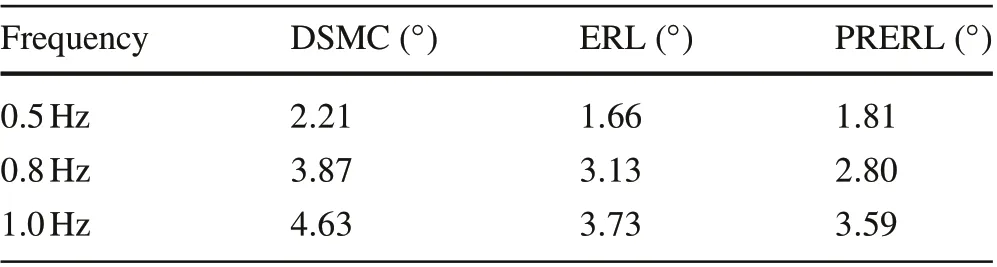
Table 4 RMSE of comparative controllers regarding high-frequency sinusoidal tracking experiment

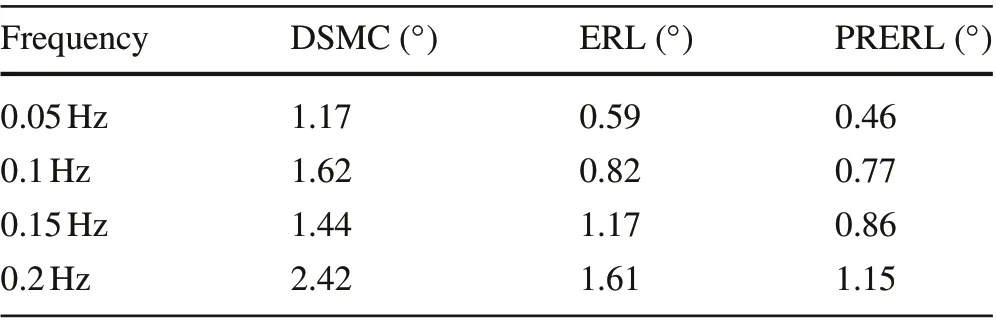
Table 5 RMSE of comparative controllers with regard to triangular tracking experiment

4.3 Tracking low-frequency triangular trajectories

As an extension to examine the tracking performance of the designed controller,the triangle signal wave is set to be the reference trajectory. In this case, the amplitude of desired input signal is 20◦with frequencies ranging from 0.05 to 0.2Hz,and the illustrative tracking results of three comparative controllers are shown in Fig.7.As a consequence of the hysteresis issue and slow response behavior of the PAMs,the changing in direction of the two PAMs can lead to an increase in steady error.Nevertheless,it can be derived from these figures that at the changing direction point, the proposed PRERL achieves fast convergence rates in terms of error which maintains the tracking error within a considerable small range of under 2◦.This advantage mainly comes from the property of PRERL,which guarantees the reduction of reaching time and chattering alleviation.Table 5 demonstrates the quantitative comparisons of RMSEs among all controllers.Asregardsfromthistable,theeffectivenessofthe PRERL is once again verified with the best performance,outstanding tracking accuracy,and chattering-free control signal even though in the presence of hysteresis and disturbance.

4.4 Tracking sinusoidal trajectories with load

To examine the stability and robustness of the proposed PRERL,in this subsection,a 5kg load is added to the experimental system as an external disturbance element.This 5kg mass is attached to the PAMs structure through the pulley mechanism as shown in Fig. 2, and will be employed at the later half of the second period after the system enters steady state.Let the sinusoidal signal be the desired trajectory and the amplitude of the reference signal is 20◦.Figure8 illustrates the two particular tracking results comparing the PRERLcontrolleranditstwocounterparts.Itcanbeobserved that the DSMC controller performs even worse in the case of a 5kg load.The DSMC controller poorly compensates for the impact of load and takes a noticeable amount of time to regain the tracking performance. The maximum steady-state error after adding load is rather high up to 5◦.Meanwhile,the ERLbased DSMC can give a better control performance under loading conditions with a quick recover after load added but still witnessed chatters as shown in Fig. 8a. However, the effectiveness of the proposed controller is once again proven withthebesttrackingperformanceevenwithhaving5kgload as the external disturbance.The PRERL is able to maintain excellent tracking accuracy and shows no issue dealing with load with less than 2◦of the steady-state error.As expected,the PRERL-based controller also shows no sign of chattering behavior which comes from the adaption of the control gain.Table 6 summarizes quantitative comparisons of the three controllers.

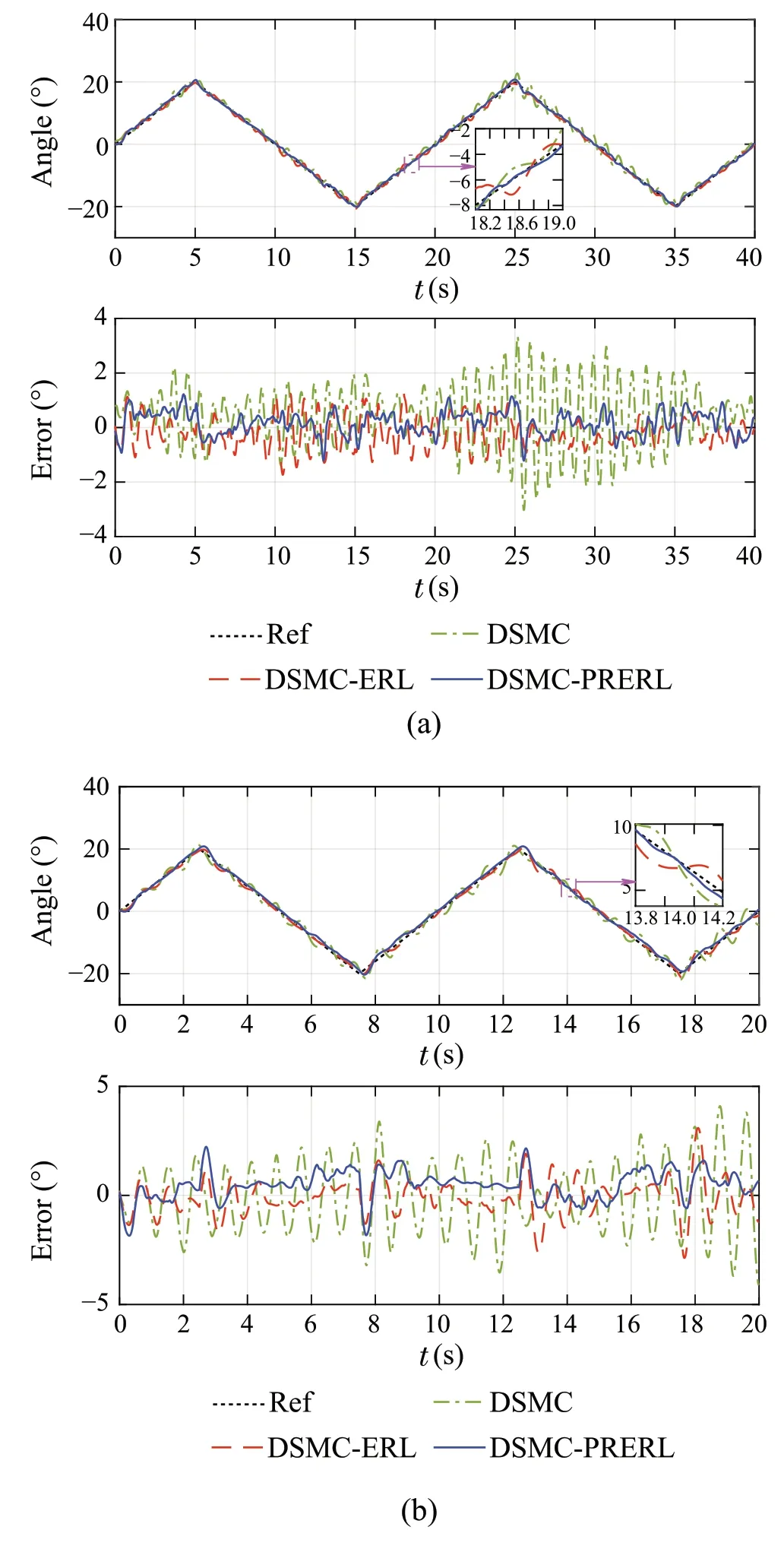
Fig.7 Experiment results for tracking low-frequency triangular trajectory.a 0.05Hz,b 0.1Hz

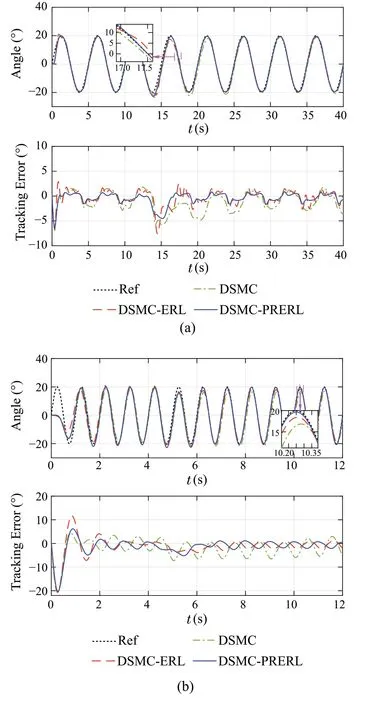
Fig. 8 Experiment results for tracking sinusoidal trajectories when driving load m =5kg.a 0.2Hz,b 1.0Hz

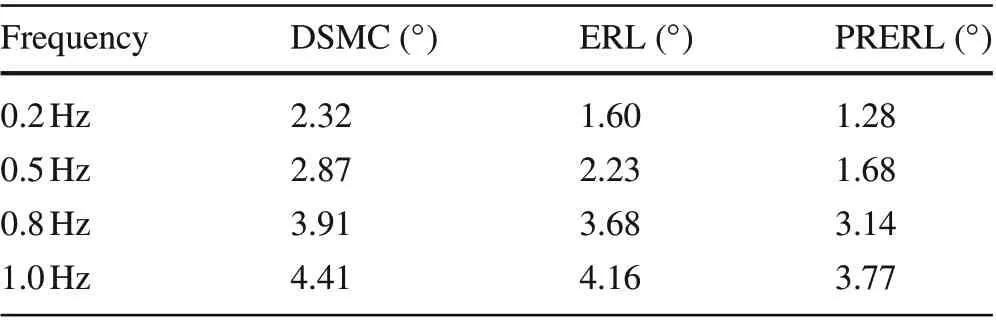
Table 6 MSE of comparative controllers with regard to sinusoidal tracking experiment with m =5kg of load

5 Conclusion and discussion

In this paper, a discrete-time sliding mode controller based on power rate exponential reaching law has been proposed for a mechanism of PAMs in antagonistic configuration.The power rate exponential term is introduced into the controller design to attenuate the chattering and enhance the tracking performance of DSMC in both transient and steady state.Its superb lies in the adaption to the variation of switching function by letting gain vary and fast response during reaching phase. The tracking accuracy of the PRERL has been analyzed and the effectiveness of the proposed reaching law has been verified through various scenarios.Finally,experiment results clearly show the validity of the designed controller in dealing with the chattering phenomenon and achieving satisfactory tracking performance.

It may be noted from this work is that the simplified model in system identification brings some advantages compared to others such as the hysteresis model[12,13].This leads to the fact that the control algorithm is much less affected by noisesensitive model parameters and measurement errors.On the other hand, experiment results show the excellent tracking accuracy and outstanding chattering reduction of the proposed controller in all cases given. Although there exists a drawback in the slow response speed in the transient state,the practical application of the proposed DSMC-PRERL is promising. Future works would be the development of this controller its applicability in the rehabilitation field,specifically in leg-gait pattern tracking for medical purposes.