Cooperative distributed state estimation:resilient topologies against smart spoofers

Mostafa Safi1

Received:25 December 2021/Revised:19 August 2022/Accepted:22 August 2022/Published online:9 November 2022

©The Author(s),under exclusive licence to South China University of Technology and Academy of Mathematics and Systems Science,Chinese Academy of Sciences 2022

Abstract A network of observers is considered,where through asynchronous(with bounded delay)communications,they cooperatively estimate the states of a linear time-invariant(LTI)system.In such a setting,a new type of adversary might affect the observation processbyimpersonatingtheidentityoftheregularnode,whichisaviolationofcommunicationauthenticity.Theseadversaries also inherit the capabilities of Byzantine nodes, making them more powerful threats called smart spoofers. We show how asynchronous networks are vulnerable to smart spoofing attack.In the estimation scheme considered in this paper,information flows from the sets of source nodes,which can detect a portion of the state variables each,to the other follower nodes.The regular nodes,to avoid being misguided by the threats,distributively filter the extreme values received from the nodes in their neighborhood.Topological conditions based on strong robustness are proposed to guarantee the convergence.Two simulation scenarios are provided to verify the results.

Keywords Cyber-physical systems·Smart spoofing·Distributed resilient algorithm·Secure observers

1 Introduction

Security is becoming an increasingly important concern for the stability and safety of networked control systems.Nowadays, in large-scale control systems, communication channels connecting various physical components for realtime measurement and control mostly make use of general purpose cyber-networks such as the Internet and wireless networks, which create vulnerabilities to adversarial intrusions.While conventional network security-based measures may be partially effective,novel resiliency methods explicitly taking the dynamical nature of physical components into account should be developed as any failure in security of the cyber components in such systems may turn into irrecoverable harms to the physical infrastructure.

Security experts define various security goals including(i)Confidentiality, ensuring privacy of important data against outside eavesdroppers;(ii)Integrity,maintaining fidelity of system signals;(iii)Availability,capability of timely having access to the required signals; (iv)Authenticity, verifying identity of each signal; (v)Authorization, adjusting legitimacy of access by each component to other parts of the system; and (vi)Accountability, detection of any potential attacks and faults in the system[1].

In this paper, we considermasquerading,spoofing, orimpersonationattack strategy on cyber-physical networked systems, which is a threat of authenticity. A broad range of wired and wireless networks including sensor networks,in-vehicle networks,and Internet-based networks are susceptible to be threatened by spoofing. For instance, the reader can refer to[2]for satellite mobile communication networks,[3]for mobile ad hoc networks,and[4]for CAN-based networks. Spoof-resiliency techniques would be essential for all of these network setups to detect and/or mitigate the adversarial effects.However,mostly in literature,the spoofresilient algorithms are studied for the interactions between only two agents:a spoofer and a normal[5–9].For example,[6]presents an application of spatial processing methods for spoofing detection and mitigation.Also,a GPS spoofing scenario is formulated as a constrained optimization problem and an effective solution is provided to compute the falsified GPS measurement of each time instant [7]. The false-data injection attack on unmanned vehicles is investigated in[8].Although, this differs a little from spoofing attacks. The attacker masquerades as a disturbance for control system of a vehicle and deviates its path smoothly.Furthermore,a gametheoretic approach is developed in[9]to counteract spoofing attacks.However,a common point all the above researches share is that there is no network of agents. Only two-side interplay scenarios are considered, where the spoofing or masquerading is the attacking method.Recently though,Gil et al. [10,11] focused on the sequels of spoofing attack on the network of agents. However, both of these references use physical fingerprints of communication signals to undo the attacks, which is a different approach and cannot resist against omniscient adversaries in practice. Despite [10], in our work, the attackers do not leave any sign and thus the regular nodes cannot identify them.Also,omniscient attackers in our setup could break any type of signal encryption and perform masquerading.Particularly,our emphasis is on the resiliency of a network in terms of its topology that is a more basic level of counteraction to cyber threats.Moreover,in [10], attackers cause an availability threat by jamming the server with fake identities,which is a special case of our adversarialmodel.Wecombineadversarialcapabilitiesofthe so-calledByzantinemodel,which is an integrity attack capable of sending inconsistent erroneous signals to the receivers introduced and used in[12,13],with spoofing,that is use of other nodes’identities to send data on their behalf,and introduce a novel and more powerful adversarial model calledsmart spoofer. In [14], resiliency of synchronous networks is investigated against mobile Byzantine adversaries that are different from our adversarial model. In our setting, smart spoofers can use the asynchrony of network communications to mislead the nodes with impersonated identities.

One of the targets of spoofers in network systems would be inserting erroneous values into the distributed state estimations performed by the nodes.Distributed state estimation algorithms are extensively studied in[15–18].However,all these research works focused on the interaction between dynamic system,observers and the graph topology.A minimum cost communication graph which enables limited communication for decentralized estimation is investigated in[15].The interplay between network connectivity,global observability,and system instability is studied in[16].Necessary and sufficient conditions for existence of distributed observers are studied in [17]. Also, Wang and Morse [18]generalized distributed observer design for LTI systems with singular transition matrices. None of the above research works consider communication security among the physical and cyber layers.The resilience of distributed observers against cyber attacks has recently received more attention. For instance, the resiliency of LTI systems has been investigated in[19,20]against Byzantine attacks.However,our adversarial model is more complex by considering the impersonation capability of adversaries. We also consider asynchrony and delays in communications and propose a randomization strategy for relaxing the imposed topology constraints for secure distributed estimation problem.

In the current paper,we consider impersonation on a network of distributed observers for an LTI system. Like the network communication settings in [21,22], the observers communicate with bounded delays and asynchrony; however,they must deal with stronger attacks,i.e.,smart spoofing. Similar to [19], the regular (un-attacked) nodes are partitioned to source nodes and follower nodes,where source nodes can detect the corresponding eigenvalues and via distributively constructing a directed acyclic graph(DAG),the associated state estimates disseminate through the network.In both DAG construction and estimation propagation,smart spoofers interfere to avoid convergence.We present a strategy based on local filtering that is able to defend against smart spoofing and define local sub-graphs to mimic the graph behavior for analysis of the estimation convergence, turning into sufficient conditions on network topology based on graph robustness that is a connectivity measure(see[13,23]for application of similar filtering algorithms in consensus problem). Consistency of the defined spoofing model with the network security literature,consideration of delays,asynchrony, and accurate assumptions in network communications make our proposed algorithms, update rule, and concluding results more practical in real world applications.In the development of our results and the proofs,we adopted the concept of motifs, the smallest possible subgraphs of the original network with certain properties,as a new proof technique.We analyze how the information is disseminated through the motifs.All in all,the main contributions of this paper to the literature are:

• Introducing, modeling and formulating a new type of cyber attack in asynchronous network settings which inherits the properties of both Byzantine adversaries and spoofing agents,called smart spoofing.

• Analyzing the vulnerability of asynchronous networks to smart spoofers and proposing a resilient distributed state estimation strategy for a class of LTI systems.

• Using motifs,as the smallest possible repeating patterns in a network, to mathematically analyze the topology constraints required for convergence of the distributed state estimation.

• Presenting a randomized update rule to relax the spoofresilient topology constraint required for convergence of the distributed state estimation.

The paper is organized as follows.The preliminaries and problem statement come in Sect.2.In Sect.3,we take a look at the resilient distributed estimation scheme and the local filtering-based algorithm that we used in this paper.Our main results are presented in Sect.4.We put forward the simulation results in Sect.5.Finally,we conclude the paper and discuss the future tendency of the research in Sect.6.

2 Preliminaries and problem statement

2.1 Notations

2.1.1 Graph theory

A directed graph is represented byG=(V,E),where the set of nodes and edges are represented byV= {1,...,N}andE⊆V×V,respectively.An edge from nodejpointing to nodeiimplies data transmission from nodejto nodeiand is denoted by(j,i). The neighborhood of thei-th node is defined by the setNi= {j|(j,i) ∈E}.A nodejis said to be an outgoing neighbor of nodeiif(i,j)∈E.A spanning sub-graph forGis a sub-graph ofGwhich contains every vertex ofG.Consider nodev1tovpofG.A path is a sequence(v1,v2,...,vp)inwhich(vi,vi+1)∈Efori=1,...,p−1.The length of a path is measured by its number of edges.A cycle is a sequence(v1,v2,...,vp,v1)in which(vi,vi+1)∈Efori=1,...,p−1 and(vp,v1)∈E.A directed acyclic graph(DAG)is a directed graph which has no cycles.

For the consensus-based state estimation rule designed in this paper,the critical topological notion is graph robustness,which is a connectivity measure of graphs(see[24]).

Definition 1(r-reachable set)For a graphG=(V,E)and a setC⊂V,we say thatCis anr-reachable set if there exists ani∈Csuch that|NiC|≥r,wherer∈N+.

Definition 2(Strongly r-robust w.r.t.S) For a graphG=(V,E), a set of nodesS⊂Vandr∈N+, we say thatGis stronglyr-robust with respect toS,if for any non-empty subsetC⊆VS,Cisr-reachable.

2.1.2 Linear algebra

The set of all eigenvalues of a matrixAis denoted byσ(A).The set of all marginally stable and unstable eigenvalues of a matrixAis denoted byσU(A)={λ∈σ(A)||λ|≥1}.We useaA(λ)andgA(λ)to denote the algebraic and geometric multiplicities, respectively, of an eigenvalueλ∈σ(A). An eigenvalueλis said to be simple ifaA(λ)=gA(λ)=1.

2.2 System dynamics and distributed observers

Consider the following discrete-time LTI system:

wherek∈N is the discrete-time index,x[k] ∈Rnis the state vector andA∈Rn×nis the system matrix.The system

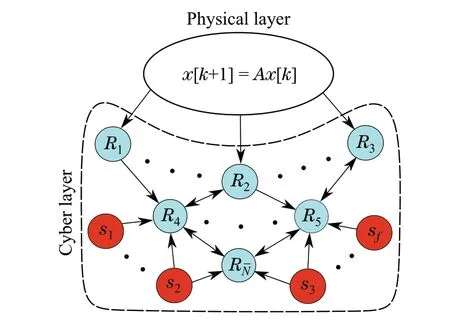
Fig.1 A typical cyber-physical system:in the physical layer,the plant dynamic(maybe unstable in some modes)propagates over time.In the cyber layer,the plant’s outputs are monitored by a network of distributed observers(R1,R2,...,R ¯N)while only some of them are directly connected to the plant. The network is threatened by adversarial nodes(s1,s2,...,s f)

is observed by anN-node networkG=(V,E). Access of thei-th node to the measurement of time instantkis given by

whereyi[k] ∈RriandCi∈Rri×n. For computational or control purposes, each node needs to estimate the entire system statex[k]. Nodes of the networkGare calleddistributed observersif they maintain and update the estimates using only their own measurements and those received from their neighbors.Figure1 shows the layout of a typical cyberphysical system threatened by adversarial nodes. Let ˆxi[k]denote the state estimate of nodeiat each time stepk.The following definition describes the objective of the distributed estimation scheme.

Definition 3(Omniscience) Over theN-node networkG,the distributed observers are said to achieve omniscience if limk→∞|ˆxi[k]−x[k]|=0,∀i∈{1,2,...,N}.

2.3 Adversarial model

We consider an adversarial model that is able to threaten the following system protection services:authentication,authorization,confidentiality,integrityandavailability. In what follows,we formally define the abilities of such an adversarial node.

Definition 4(Smart spoofer)An adversarial node is called asmart spooferif it has the following capabilities:

1. Theadversarialnodecanhavecompleteknowledgeabout the topology,plant dynamics,and information flow over the network at all time-steps.

2. The adversarial node can refuse to perform any preassigned algorithm and can send arbitrary values to each of its neighbors at the same time step.

3. The adversarial node can send its data with intended delays and asynchrony.

4. The adversarial node can impersonate other nodes and send arbitrary data with their identities.

The first two actions are performed by Byzantine adversaries, while the last one is performed by a threat calledspoofingormasqueradingin [1] that directly threatens the authentication among systems’ protection services. In fact,the introduced adversarial model is an advanced spoofing threat with additional capabilities of Byzantine adversaries that we callsmart spoofing. Note that we use the terms“spoof”and“impersonate”interchangeably in this paper.

It is apparent that no distributed estimation algorithm would succeed if all the nodes are adversarial.Therefore,the set of nodesVis partitioned into two subsets of regular nodes and adversarial nodes denoted byRandA=VR,respectively.Intheliteratureofdistributedfault-tolerantalgorithms,a common assumption is to assign an upper boundfto the total number of adversarial nodes in the network, which is known asf-total adversarial model.To consider a large number of adversaries in large-scale networks, locally bounded fault models are used,as in[25],defined below.

Definition 5(f-local smart spoofer model)A setAof smart spoofers isf-locally bounded if it contains at mostfsmart spoofers in the neighborhood of any of the regular nodes,i.e.,|Ni∩A|≤f,∀i∈VA.

Similarly, any distributed estimation algorithm fails if a smart spoofer can impersonate all the network nodes.Thus,to tackle the problem, we impose an upper bound for the number of nodes that smart spoofers can send data on their behalf as follows.

Definition 6(Capacity of smart spoofers) The maximum number of nodes that a smart spoofer can send data on their behalf at each time step,including itself,represents its capacity and is denoted byα≥1.

2.4 Problem statement

We aim to formulate the resilient version of omniscience problem (Definition3), where the network is under smart spoofers’attack with two challenging constraints on the network communications,i.e.,asynchrony and delays.Accordingly, we set the following assumptions on the network communications protocol remarking the practical aspects of our results.

Assumption 1All nodes update by a global clock. This means that the sampling timeTis the same for all observers.

Assumption 2All nodes communicate through serial links and have access to only the last data packet they have received from neighbor nodes.

Assumption 3All nodes make,at least,one update within ¯ksteps and communication delays are upper bounded by ¯τ.

Referring to the introduced LTI dynamic system and the observation model of the network, we put forth a more complicated version of the standard omniscience problem(Definition 3)in the following definition.

Definition 7(Resilient omniscience)Given a system dynamics of the form (1), a network represented by the graphG,and an observer model at each node given by (2), a state estimation design is said to achieveresilient omniscienceif limk→∞|ˆxi[k]−x[k]|=0,∀i∈R,regardless of the actions of anyf-locally bounded set of smart spoofers.

This paper investigates the design of a distributed estimation scheme,proper to cope with smart spoofers threatening a given cyber network that is observing an LTI system.For this purpose,based on the assumptions on the network communications protocol and the smart spoofer adversarial model,we first present the distributed estimation scheme under a specific network topology. Next, we analyze the required topology constraints which guarantee resilient omniscience of all regular nodes that update their estimates using the proposed estimation strategy.

3 Resilient distributed observers

Under Byzantine adversarial model introduced in [12], the network achieves omniscience by distributed observers proposed in[19].The design performs observation task by separating detectable and undetectable eigenvalues of the system and the related states. Here, we use a similar scheme with a different distributed estimation rule, proper for resilient omniscience defined in Definition 7. To this end, consider a Jordan canonical decomposition of state transition matrixAwith the following assumption on its eigenvalues. This assumption is made for sake of simplicity,is not restrictive,and can be relaxed by some extra mathematical efforts and the techniques denoted in[19],which is not the focus of this paper.

Assumption 4Eigenvalues ofAare real and simple.

This assumption allows us to diagonalizeAby the coordinate transformation matrixΨ=[ψ1,...,ψn],whereψ1,...,ψnarenlinearly independent eigenvectors ofA. Withz[k] =Ψ−1x[k],the system(1)is transformed into the form

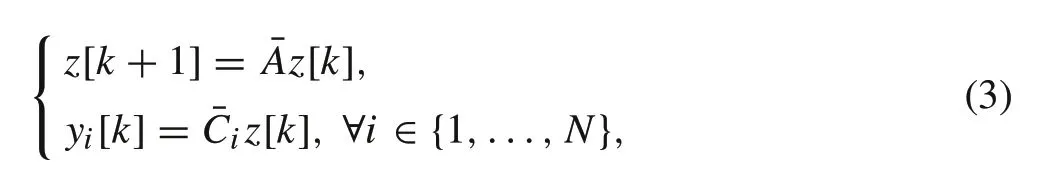
Definition 8(Source nodes and follower nodes) For eachλ j∈σU(A),the set of nodes that can detectλ jis denoted byS j,and is called the set of source nodes forλ j.The rest of the nodes are called follower nodes.

Each regular node,depending on being a source node or a follower node forλ j,adopts a different strategy for estimating the related states.

3.1 State estimation by source nodes

Referring to[19],each regular nodeirelies on its own measurements and uses a local Luenberger observer to estimate a patch of the statesDiassociated to allλ j∈Di.To this end,letΛi∈Rρi×ρi(recallρi=|Di|)be a diagonal matrix consists of the detectable eigenvalues inDiandDi∈Rri×ρistand for the columns ofcorresponding to those eigenvalues.Then we have

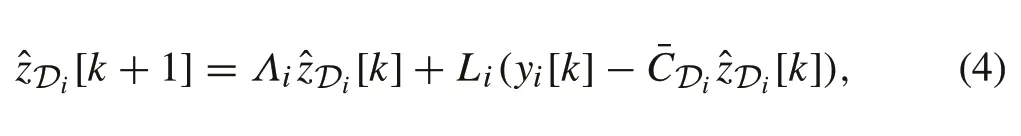
where∈Rρi×riis the observer gain matrix at nodei.Since the pair(Λi,Di)is detectable,Lican be chosen in a way that(Λi−LiDi)is Schur stable,so limk→∞|[k]−[k]|=0 based on Assumption 4.

3.2 Distributed state estimation by follower nodes

A regular nodeicannot estimate a portion of the states associated with its undetectable eigenvalues of the system. In fact,the regular nodeiis a follower node in estimating the sub-state related to the eigenvaluesλ j∈Uiand needs to receive information from its neighbors through a directed acyclic graph for eachλ j(defined later) rooted in the set of associated source nodes.In what follows,we propose an updating rule for the follower nodeiaccomplishing its estimation task in a network with communication delays andpartial asynchrony.1

There is a major difference between resilient distributed state estimation rather than resilient consensus using local filtering presented in previous research works such as[22].

1 The termpartial asynchronyrefers to the case where nodes share some level of synchrony by having the same sampling times;however,they make updates at different times based on bounded information delays[26].Considering asynchronous network communications and observability of dynamics of the physical layer is a new challenge in design of the update rule and leads to a totally different convergence analysis.Combining the ideas behind the consensus update rules in [19,22], we present a novel update rule with the following algorithm based on localfiltering method for nodeito update its own state estimate forλ j∈Ui.

1. Each regular nodei, at each time stepkwhen it wants toupdateits estimate,gathersthe stateestimate ofzj[k]lastlyreceived from only thenodes in⊆Ni(Nijrepresents the setof neighbors in the DAG related toλjthat is selected by Algorithm 1 for each regular nodei,which will be proposed later)and arranges them from the largest to the smallest.

2. Nodeidrops the largest and smallest(β+1)festimates(βwillbedefinedlater)andexecutesthefollowingupdate rule:

In practice,each nodeihas a memory for each of its neighbors wherestores themost recentlyreceiveddata.Nodeiuses the most recent estimate values received from its neigbors inin update rule(5),regardless of delays and asynchrony in communications.

4 Main results

In this section,we provide the main results of the paper giving the analysis of the spoof-resilient distributed estimation strategy and the topology constraints under which our adopted algorithms and update rule succeed.

First, we consider how harsh the misbehavior effects of a smart spoofer would be in the network. In Definition 6,we introduced the spoofing capacity in each time step.In the following lemma,we generalize capacity of smart spoofers for a period of time.

Lemma 1Let Assumption3hold and capacity of a smart spoofer be α.Then,each smart spoofer is able to send data on behalf of β=α¯k−1regular nodes within each consecutive¯k steps.

ProofAccording to Definition 6, a smart spoofer can send data on behalf ofαnodes including itself at each time step.Also,according to Assumption 3,all nodes have to make at least one update within consecutivesteps(note that if a node does not follow this rule can be detected as an adversarial node by the regular nodes).Consider the time intervalk+1 ≤t≤k+.Let the smart spoofer choose to make an update with its own identity att=ks,wherek+1 ≤ks≤k+ ¯k.Considering each consecutive ¯ksteps, the smart spoofershasα−1 capacity for impersonation atksandαcapacity in other−1 steps.Therefore,the smart spoofer is able to impersonateα−1 nodes overall within ¯ksteps, i.e.,α−1+α(−1)=α¯k−1. ■In fact,Lemma 1 indicates that we cannot simply replace the smart spoofers and impersonated nodes with Byzantine nodes.Because the key question is that how many Byzantine nodes have the same effect of a smart spoofer with capacityα. This is what we mathematically clarified in Lemma 1. Asynchrony lets the adversarial nodes spoof a specific number of regular nodes within each ¯ktime-steps.Besides,from adversarial nodes’perspective,this spoofing(and sending false-data packets) must be continued for all the future time—in every¯ksteps-in order to be effective.Thus,the distributed algorithms of regular nodes must be modified to be resilient against the attack.In other words,network providers need to be aware that in a network with asynchrony(almost all the networks are practically asynchronous), there is the possibility of stronger attacks rather than Byzantine attacks.The following necessary condition on the network communications formally states when a smart spoofer can impersonate regular nodes.

Proposition 1Consider a network of nodes interconnected by complete graph G,which contains smart spoofer s∈,where i∈R.Suppose that s is able to impersonate,at least,one regular node within each consecutive¯k steps(β> 0).Smart spoofer s can impersonate a regular node ℓ∈∩R for node i at a time instant t>k only if the packet which is broadcast by node ℓ at time instant t=k is received by node i with delayℓ[k]+τiℓ[k]>0.

ProofWe prove by contradiction. Considering Assumption 1,let nodeℓ∈broadcast a data packet att=kand nodei∈Rreceives the packet at the same time(τiℓ[k]=0)and use it for its next update at the same time(～kiℓ[k] = 0).Also, suppose that smart spoofersdecides to impersonate nodeℓfor nodei.There are two possibilities for the arrival time of the packet sent bystoi.The packet can arrive either before or after the timet=k(the time instantt=kis excluded as it contradicts Assumption 2).In case the packet sent bysarrives at any timet>k, the nodeihas already accepted the last packet it received,that is,the packet of nodeℓreceived att=k,and has already made an update.Otherwise,if the packet sent bysarrives at any timet＜k,theniwill receive the packet sent by nodeℓatt=kand since,according to Assumption 2,all nodes only access the last data packet they receive.In either case,the smart spoofersfails to impersonate nodeℓfor nodei, which is a contradiction.This completes the proof. ■

Note that the necessary condition of Proposition 1 is independent of amounts of communication delays. This is because we would like to deal with smart spoofers that can impose arbitrarily bounded amount of delays on their links to the regular nodes,that is,if a smart spoofer wants to impersonate nodeℓ∈, it can arrange to send the packet to nodeiafter nodeℓwith appropriate delay so that it will be received after the packet sent by nodeℓ.Then,nodeiaccepts a packet sent byswith identity of nodeℓas it is the last packet received.

According to Proposition 1, the best case for the regular nodeiis that bothiℓ[k] = 0 andτiℓ[k] = 0, so the smart spoofers in the neighborhood oficannot impersonate neighbors of the nodei. However, even if we suppose thatiℓ[k] = 0, i.e., nodeihas not any lag in updating its estimate using the last data received from nodeℓ,regular nodes cannot be sure about spoofing attack.In practice,the regular nodes cannot guess,before receiving a packet,whether it will be received with delay and,if so,how much the delay will be(although communication links’delays in real network systems are inevitable).Besides,as we said,smart spoofers can send data packets with intended delays.Therefore,the regular nodes must be aware that all the communications may be done with delays in each time step.Therefore,to consider the worst case,we develop our further results on required topology constraints by assuming that the necessary condition on delays is satisfied for all time in the network.

4.1 Spoof-resilient mode estimation directed acyclic graph(SR-MEDAG)

Recall the local filtering for resilient consensus-based estimation law(5).Inspired by the algorithm presented in[19],for construction of directed acyclic graphs associated with undetectable eigenvalues of an LTI system, we present a spoof-resilient algorithm which is distributively executed by all the regular nodes. The overall distributed estimation scheme constitutes the construction of these sub-graphs and the prescribed local filtering-based algorithm which are per-formed in parallel. In what follows, we define the directed acyclic graphs that are paths for information flow over the network.

Algorithm 1 SR-MEDAG construction algorithm

Definition 9(SR-MEDAG)Foreacheigenvalueλ j∈σU(A),the spanning sub-graphGj=(V,Ej)ofGis SR-MEDAG if it has the following properties:

Interestingly, it is not necessary for the regular nodes to knowj(in that case, they have to execute the construction algorithm for all the future time not up toj).Indeed,each regular nodeican begin updating its state estimates in parallel as soon as it setsci(j) = 1 forλ jalthough the SR-MEDAG construction phase has not been terminated yet.However,we know that the construction phase will be terminatedatsometimeinstantinthefuture(boundedbyj)when all regular nodes will be able to update their own state estimates corresponding to each of the undetectable eigenvalues using the distributed consensus-based rule(5).In this regard,consider that delay and asynchrony do not affect the output of the algorithm for each regular nodei.Because nodeiwaits until it receives the predefined messageχ jfrom a specified number of nodes regardless of the time it takes.Indeed,asynchrony and bounded delays only postpone termination of the algorithm.

Furthermore, one may concern that some of the regular nodes are exposed to be impersonated by smart spoofers at any time while they are executing the construction algorithm.In fact, each smart spoofer not only can impersonate regular nodes(by sending arbitrary messages other than the true messageχ jon behalf of them) but also can misbehave as follows:

(i) It chooses to transmit any message different from the true messageχ jfrom start to termination of the construction phase.

(ii) It transmits the true message before the counter value is triggered by a regular node.

(iii) It chooses not to transmit a message at all.

2 Weusedthetermbroadcastconsideringthecaseofwirelessnetworks.Regular nodes may transmit the information to their known outgoing neighbors in wired networks.

In the first case,regular nodes are able to identify the adversarial node as it goes against the rules of Algorithm 1.In the latter two cases,the adversarial node is undetectable by regular nodes relying just on local information.However,later we discuss constraints on the graph topology so that adversarial nodes fail to make any problem neither for the construction algorithm nor the estimation process.

It is noteworthy that the upper bound for the parameter¯K jin Algorithm 1 is a function of the parameterβ,which is the capacity that asynchrony provides for smart spoofers to impersonate regular nodes.This upper bound would be different if we consider simply more Byzantine nodes instead of spoofers and impersonated nodes.Actually,another contribution of our paper with respect to [19] is the MEDAG construction algorithm and its convergence time.In the case of synchronous networks, each regular node updates only once and goes to sleep, while, in asynchronous networks,regular nodes have to continue updating up to ¯K jtime-steps in order to complete the SR-MEDAG construction.

In the following theorem, we show that the sub-graphs distributively found by the regular nodes,after termination of the construction phase,satisfy properties of the SR-MEDAG.

Theorem 1If the SR-MEDAG construction phase terminates for λ j∈σU(A),there exists a sub-graph Gj satisfying all the properties of an SR-MEDAG.

ProofFirst,we prove by contradiction that the spanning subgraphGjis a directed acyclic graph. Suppose there is a directed cyclei Pi,whereiand the nodes inPbelongs toR.The pathPoriginates fromiwhich changes its counter valueci(j)from 0 to 1 and begins transmittingχ jto its neighbors at a time instantt=Let the last node on the pathPbeℓ.Clearly,nodeireceives data from nodeℓat a time instantt>. As an edge fromℓis pointing to nodei, nodeiis supposed to receive the messageχ jfrom nodeℓeven when its counter valueci(j)is set to 1.This contradicts what nodeihas to do according to Algorithm 1. The same argument holds for every regular node belonging toGj.

We intentionally used the minimum number of variables to be communicated in SR-MEDAG so as to avoid potential masquerading threats caused by those variables. For example,it is not possible for regular nodes to realize their layer order inGjas they cannot identify which of their parent nodes are spoofed. To clarify this, consider a regular nodeiin. The regular node has to receive 2(β+ 1)f+ 1 incoming edges from the nodes inwhich broadcast their layer numbers so that the nodeican realize its own layer number by sorting the received values and selecting the maximum as the previous layer number.However,smart spoofers can impersonate some of these nodes and send a wrong layer number behind of them. Thus, the nodeican be deceived about the maximum layer number it received.Interestingly,in our method,there is no need that the regular nodes know their layer orders since they only needs to know 2(β+1)f+1 of their parent nodes to succeed in the estimation phase.Therefore,the construction algorithm can still be executed distributedly.Moreover,our strategy succeeds even if some of the source nodes inS jare smart spoofers.

4.2 Analysis of the resilient distributed estimation strategy

In this section, we introduce a repeating pattern sub-graph which is used to simplify the analysis of our distributed estimation scheme. These sub-graphs are constructed and organized for each regular node according to its incoming edges from smart spoofers and other regular neighbors.Note that they may have overlaps in specific nodes and are defined as follows.

We aim to associate each motifto each nodeito ensure that a smart spoofer or an impersonated node cannot deviate the estimation of the nodei.In fact,each motif is the smallest sub-graph ofGjwhich is resilient against Byzantine attacks.Note that impersonated regular nodes are potential Byzantine adversaries since smart spoofers can use their identities to send arbitrary values to their neighbors.

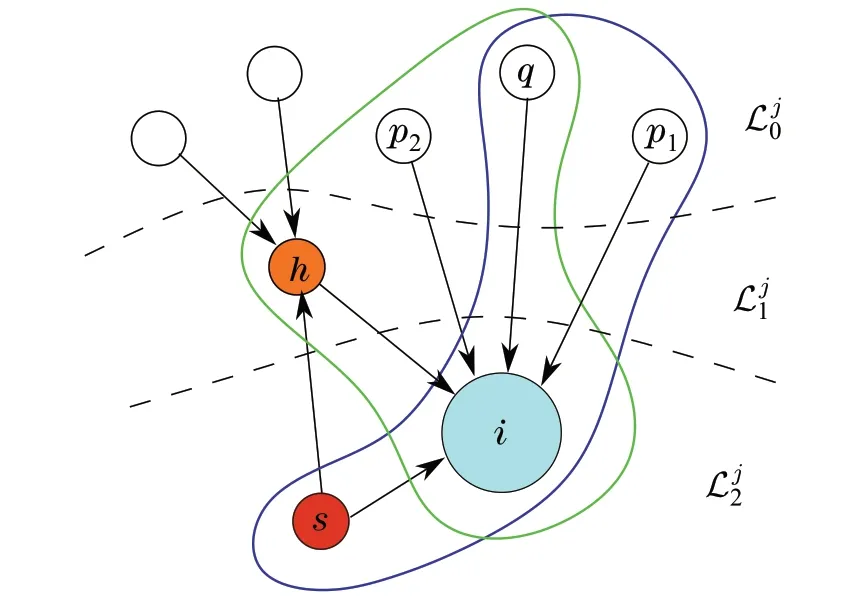
Fig.2 Motifsfoundin SR-MEDAGof Gj forf =1 and β=1with theregularnode iin,threeregularparentnodesof iin (p1and p2 areindependentnodes ofthemotifs andq is acommon node)anda parentnodeinwhich canbeimpersonated bya smartspoofer.Here,n ode his impersonated by the smart spoofer s for the nodei

Definition 11(Independent and common nodes)Consider ¯γmotifs associated withhlandpraround the regular nodeidenoted byGj i(l,r),r= 1,2,..., ¯γ. Letpγbe a regular node in the setVij(l,r),r=γ.Then,pγis an independent node ifpγ/∈Vij(l,r)∀r/=γ.A node that is not independent is called common.

The analysis strategy is to find the set of motifs around nodei∈Ljmsuch that they have only one common node.The following lemma determines the number of such motifs and investigates the possibility of this strategy(see Fig.2 for an example).

Lemma 2Consider the network G which contains an SRMEDAG Gj for each λ j∈σU(A).There exist at least(β+1)f motifs around each regular node i∈L,where each motif has at least an independent node.

ProofFor each regular nodei∈, referring to Definition 10, consider partitioning ofinto subsets {q},{pr},r= {1,2,...,}, and {hl},l= {1,2,...,}. Based on the first property of SR-MEDAGGj, we havei≥2(β+1)f+1.Underf-local smart spoofer model,there are at mostfsmart spoofers around the nodei,i.e.,|∩R|≥(2β+1)f+1. These regular nodes are parent nodes ofibased on the second property of SR-MEDAGGj. According to Lemma 1, at mostβ fof these parent nodes may be impersonated by the smart spoofers.Thus,at most(β+1)fof the nodes inN j iare whether smart spoofers or impersonated parent nodes of the nodeiwhich are partitioned as{hl},l={1,2,...,},i.e.,≤(β+1)f.We can organize at least(β+1)f+1 of the remaining parent nodes,which cannot be impersonated,to construct the motifs around the nodei.Based on Definitions 10 and 11,we pick a parent nodeqas a common node and leave the rest in the set of independent parent nodes{pr},r=1,2,...,,i.e.,≥(β+1)f.Since≥,we can find at least(β+1)fmotifs around the regular nodeisuch that all of them have one common parent nodeqand each associated with an independent parent nodeprand a nodehl.This completes the proof. ■

Figure2 exhibits two overlapping motifs.In this example,there is a smart spoofer node around the regular nodei,i.e.,f= 1. Also, it is supposed thatβ= 1. Thus, according to Lemma 2,two motifs are found around nodei.Note that smart spooferscan impersonate nodeh, so a motif has to be constructed with the nodehas the adversarial node.Also,nodeqis selected as the common node whilep1andp2are the two independent parent nodes of nodei.

Next, we use the notion of motifs to analyze estimation resilience of the networkGenhanced by the distributed estimation update rule (5) at each node against the adversarial nodes in the presence of communication delays and asynchrony. We start with regular nodei∈and generalize our analysis to the whole network afterwards.

Lemma 3Consider the network G which contains an SRMEDAG Gj for each λ j∈σU(A).Suppose that the state estimates of regular parent nodes of node i∈,for the state related to λ j,converge to zj asymptotically.Then,the local filtering-based algorithm governed by update rule(5)ensures thatlimk→∞|[k]−zj[k]| = 0in the presence ofcommunication delays and asynchrony under f-local smart spoofer model.

Now, we analyze resilience of the estimation of all the follower nodes in the whole networkGwith communication delays and asynchrony againstf-local smart spoofer model.

Lemma 4Consider the network G which contains an SRMEDAG Gj for each λ j∈σU(A).Then,for each regular node i∈R and each λ j∈Ui,the local filteringbased algorithm governed by update rule(5)ensures thatlimk→∞|[k]−zj[k]| = 0in the presence of communication delays and asynchrony under f-local smart spoofer model.

Due to the linear dynamics of the local Luenberger observers for source nodes and since the estimation error of each follower node is a linear combination of its unimpersonated parents,we infer the following corollary about the convergence rate of the follower nodes’estimation error.

Corollary 1Estimation convergence rate of all the follower nodes in the network is exponential as the estimation error of the source nodes converges to0exponentially.

Theorem 2Consider the network G which contains an SRMEDAG for each λ j∈σU(A).Then,the distributed estimation scheme governed by the Luenberger observers described by(4),and the local filtering-based algorithm governed by update rule(5),achieves resilient omniscience in the presence of communication delays and asynchrony under f-local smart spoofer model.

ProofBased on the observable canonical decomposition represented by (3), for each regular nodei, states of the dynamics system (1) are mapped and partitioned into two sub-stateszDi[k]andzUi[k]corresponding to the detectable and undetectable eigenvalues of the nodei, respectively.Using the designed Luenberger observers,i[k]converges tozDi[k]asymptotically.As an SR-MEDAG exists for eachλ j∈σU(A),the result of Lemma 4 also holds.Consequently,nodeiis able to estimatezUi[k]asymptotically even in the presence of communication delays, asynchrony and adversarial actions of smart spoofers. Combining these results,we infer that nodeican estimate the entire statez[k]which leads to resiliently observingx[k] using the transformationx[k]=Ψ z[k].This completes the proof. ■

4.3 Spoof-resilient graph topologies

In this section, we characterize graph topologies which ensures termination of the SR-MEDAG construction phase for eachλ j∈σU(A)under misbehavior of smart spoofers.

Lemma 5The SR-MEDAG construction phase terminates for λ j∈σU(A)if G is strongly3(β+ 1)f+ 1-robust w.r.t.S j.

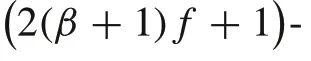
Note that the presented sufficient conditions on the topology will be the same as the case of Byzantine attacks,proposed in[19],if we set the parameterβ=0.It means that the estimation will converge for all regular nodes under a simpler topology,i.e.,strongly(3f+1)-robust w.r.t.S j, ∀λ j∈σU(A).This is consistent with the most important massage of our paper which asserts that asynchronous networks are more susceptible against cyber attacks; asynchronous networks can be threaten by adversaries that are stronger than Byzantine nodes, i.e., smart spoofers, which can use free time-steps between updates of regular nodes to impersonate some of them in order to mislead the others.

4.4 Time-varying networks

In the presented results so far,the observers over networkGwere supposed to be fixed, that is, the edge setEwas time invariant.We now reconsider the results with a partially asynchronous time-varying networkG[k]=(V,E[k])instead of the original time-invariant graphGearlier.To this end,similar to what is presented in [21], we define a jointly graph robustness measure as follows.

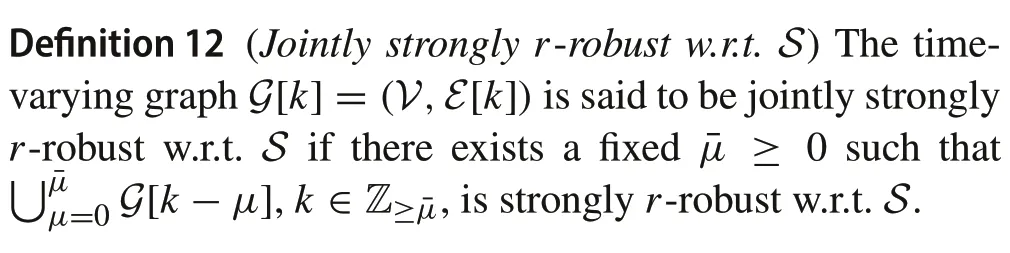
Referring to Lemma 1,the capacity of smart spoofers for impersonating regular nodes is bounded within each consecutivesteps byβ. Thus, the horizon parameter ¯μof time-varying graphG[k]has to satisfy the following inequality:

Note that, otherwise, each smart spoofer would have extra capacity to impersonate more thanβregular nodes after eachsteps.

Now,the following result states the extension of our main result(Theorem 3)for the case of time-varying networks.

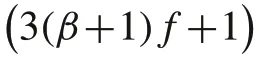
Similarly, reconsidering the case where smart spoofers do not impersonate any of the regular nodes during the SRMEDAG construction phase, the following result holds for time-varying networks.

Corollary 3Suppose that smart spoofers impersonate none of the regular nodes during SR-MEDAG construction phase.Then,the sufficient topology constraint on the network G[k]to achieve resilient omniscience is jointly strongly2(β+1)f+1-robust w.r.t.S j, ∀λ j∈σU(A),with condition(7).

These results follow Lemmas 3–5 as the time-invariant nature of the original graphGis not used in the proofs.

4.5 Randomized update rule

Consider the case that each regular node,at each time instant,randomly decides whether to update its state estimate or not.That is, the follower nodei∈Rupdates its state estimate at each time instantkwith the probability ofPi[k].Note that with such updates,the algorithm remains fully distributed.Even the probabilitiesPi[k]need not be identical.Intuitively,this is in alignment with Assumption 3 as the regular node will update at least once within each consecutive¯ksteps.With this strategy,the topology constraint required for resilient omniscience can be relaxed.This is because the smart spoofers cannot predict the update times in advance and need to use more of their spoofing capacity to make sure that the regular nodes,at each time step,receive and accept false data with fake identities;they cannot impersonate other nodes in a systematic manner in each consecutive ¯ksteps.In fact,regular nodes utilized randomization in update times as a defensive means against smart spoofers.

What follows is the modification of Theorem 3 for the suggested network with randomized updating strategy.

Theorem 4Resilient omniscience of a network with communication delays and asynchrony under the f-local smart spoofer model can be achieved using the proposed estimation scheme if each follower node i∈R,at each timeinstant k,updates using rule(5)with the probability ofPi∈(0,1]and if G is strongly3(β′+ 1)f+ 1-robustw.r.t.S j, ∀λ j∈σU(A),where β′=⎿β/¯k」+1.

ProofReferring to Lemma 1, each smart spoofer was able to impersonate at mostβregular nodes within ¯ksteps in case the smart spoofers knew when exactly each regular node updates its state estimate. Now, consider that each regular nodeimake an update at each time instantkrandomly with a probability ofPi[k]∈(0,1].Then,each smart spoofers∈Nicannot predict when exactly the nodeiupdates;so it has to impersonate the incoming neighbors of the nodeifor all the time steps within each consecutive ¯ksteps,that is¯ktimes.As a result,the smart spoofers need to dedicate more capacity to produce faulty data packets with the mimicked identities of the neighbors of the nodei.Thus,the smart spoofers will be able to impersonate ⎿β/」regular nodes for any of ¯ksteps and one regular node for a limited number of time-steps,i.e.,less than.In this situation,to ensure that the smart spoofers cannot impersonate any extra regular nodes,we defineβ′=⎿β/」+1.Accordingly,similar to the proof of Theorem 3,the required topology constraint for omniscience based on the parameterβ′is strongly3(β′+1)f+1-robust w.r.t.S j, ∀λ j∈σU(A). ■

Remark 4Based on Lemma 1,we haveβ′=⎿(α−1)/」.On the other hand,we know≥1.Therefore,it is concluded thatβ′=α−1 in the case of a synchronous network(=1)andβ′=αin an asynchronous network(>1).

5 Simulation results

In this section,we present a simulation example to demonstrate how a smart spoofer can misbehave and how it can be restrained in a given network of distributed observers.In particular,we show why the constraints on the network topology,proposed in Theorems 2 and 3,are critical for achieving resilient omniscience underf-local smart spoofer model in the presence of asynchronous communications and delays.To this end,consider the network illustrated in Fig.3.The directed edges of the graph represent all to one connections and edges pointing in both directions represent all to all connections. The network has three sets of regular nodesR1,R2,R3, and a smart spoofers(f= 1). The capacity ofsis assumed to beα= 1 and all of the nodes are supposed to make, at least, an update within= 2 steps. Thus, the parameter is set asβ=1.There are 2(β+1)fnodes in each of the setsR1andR2and 2(β+1)f+1 nodes in the setR3,where the nodes within each set are not connected.Furthermore,communication delays over the network are defined as follows:

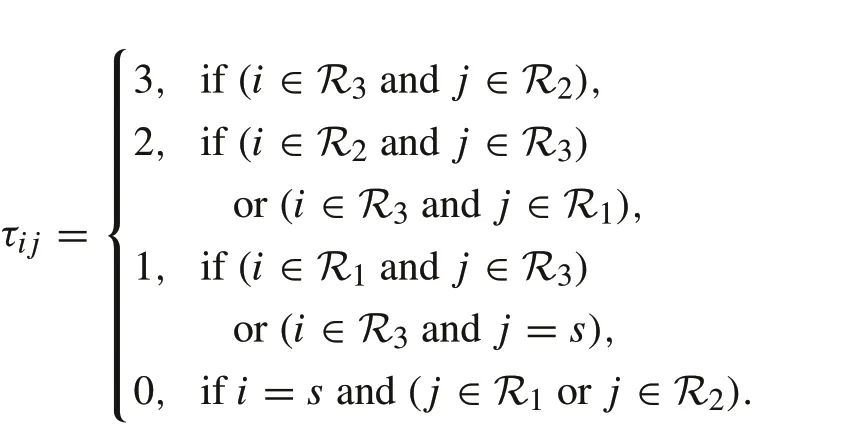
Note that the smart spoofer fully knows the dynamic system and the observation models of the regular nodes and calculates its own and the impersonated states estimations in a way that the targeting regular nodes fail to reach omniscience. Thus, to give a better intuition, we deal with the transformed dynamic system and states in our simulations;the original system can be analyzed accordingly.For sake of simplicity,we use the terms“send”and“receive”with(or), while our purpose is the original stateassociated to the.

The transition matrix of the original dynamic system and the initial state are assumed to be

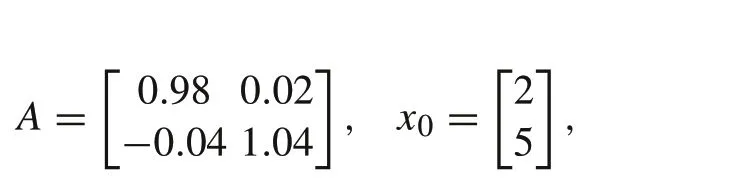
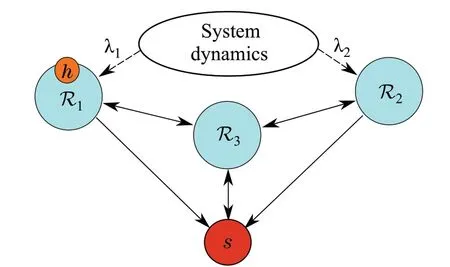
Fig.3 A sample network that is 2(β+1)f +1-robust w.r.t.λ j.Node h ∈R1 is impersonated by the smart spoofer s for the nodes in set R3

which,according to(3),are transformed by

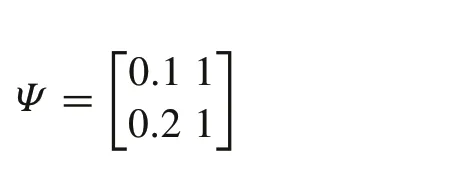
into the following diagonal system and initial state:

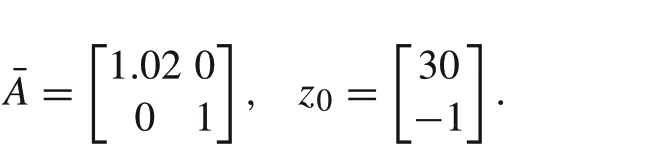
The first eigenvalue of the system(λ1=1.02)is unstable and the second one(λ2=1)is marginally stable.The observation modelofthenetworksystemisassumedtobeCi=[−1010],∀i∈R1,Ci= [2 −1], ∀i∈R2andCi= 0, ∀i∈R3.The transformation of the observation model is given byΨas= [1 0],∀i∈R1,= [0 1],∀i∈R2and ¯Ci= 0,∀i∈R3.This means that the nodes inR1are source nodes forλ1and followers forλ2as they can only detectλ1, the nodes inR2are source nodes forλ2and followers forλ1,and the nodes inR3are followers for bothλ1andλ2.Also,the nodes in the setR3and the nodesupdate at all time instants and the nodes inR1andR2update at time instantsk=m,m∈Z+.

We present the simulation results in two test scenarios.In both scenarios,the smart spoofer just impersonate only one node inR1and only for the statez1.Thus,all the nodes of the network will accurately estimate the statez2.In scenario 1,we show that the follower nodes forλ1can asymptotically estimatez1even though the smart spooferstries to mislead the follower nodes but the network finally achieves omniscience.However,in Scenario 2,the follower nodes cannot reach a true estimate ofz1as the required topology constraint for estimation(Theorem 2)is not satisfied.

Fig.4 Omniscience of the sample network: the regular source nodes in R1 asymptotically estimate z1 using Luenberger observers.The follower nodes in R2 and R3 can asymptotically estimate z1 despite of the efforts smart spoofer does for misleading them by impersonating the node h ∈R1.They also estimate z2 since there is no spoofing for λ2

Scenario 1The smart spoofer sends the message χs= 1to all the nodes in R3to pretend that it is a parent node for λ1.Although the smart spoofer can impersonate a regular node during the SR-MEDAG construction phase,it decides not to do so and goes through the estimation phase.The initial estimates of z1for nodes in R1are[0] = 100,i= 1,2and[0] = 0,i= 3,4.Also,we have[0] = 0,i∈R2,and[0]=0,i∈R3.Moreover,each regular node i∈R1uses a Luenberger observer with the gain=0.5to estimate z1.Starting the estimation phase,the smart spoofer s sends two sequences of estimate values to all the nodes in R3in a way that the receiving estimate values from the nodes in R1are eliminated in local filtering:(i)the estimate value[k] = 60,where k=m−1,m∈Z+,which keeps the smart spoofer s among the accepted neighbors of the nodes in R3as each node has to send a data packet at least in each consecutivesteps,(ii)a false estimate value[k]=30,where k=m,m∈Z≥0,on behalf of the node h= 1,h∈R1to the nodes in R3.As shown in Fig.4,all the regular nodes can estimate z1although the smart spoofer caused a deviation in the estimations of the nodes in R3(and accordingly the nodes in R2)up to time instant k=12.Note that the estimate value of[k]will not be filtered only if it converges to z1.In fact,referring to Lemma 3,estimate values of the smart spoofer are sandwiched by estimate values of the regular parent nodes,thanks to our proposed rule(5)and the network topology constraint discussed in Theorem 2.

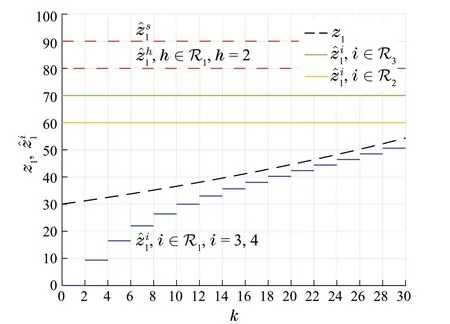
Fig.5 The smart spoofer s prevents the follower nodes for λ1 in R2 and R3 to estimate z1 by sending false estimate values on behalf of node h ∈R1 to all the nodes in R3

Scenario 2Here,the smart spoofer s sends a message χs=1to the nodes in R3while it impersonates the node p=1,p∈R1in the SR-MEDAG construction phase by setting the message χp= 0,i.e.,the node p cannot be a parent node of the nodes in R3for λ1.In other words,Algorithm 1 does not terminate in the case of λ1for the nodes in R3.In fact,the constraint on the network topology is not satisfied for the estimation of z1since the nodes in R3recognizes only2(β+1)f parent nodes for λ1.However,assume that the nodes in R3decide to start the estimation regardless of the termination of the SR-MEDAG construction phase.As a result,the smart spoofer is able to impersonate onemore regular node of the set R1this time in the estimation phase.The initial estimates of z1are given as[0]=10,i∈R1,i= 2,[0] = 0,i∈R1,i= 3,4,[0] = 6,i∈R2,and[0] = 7,i∈R3.Again,the smart spoofer s sends two sequences of estimate values to the nodes in R3in a way that the estimate values of the nodes i∈R1,i= 3,4,are eliminated in local filtering: i)the estimate value[k] =8,where k=m¯k−1,m∈Z+,which keeps the smart spoofer s among the accepted neighbors of the nodes in R3,ii)a false estimate value[k] = 9,where k=m¯k,m∈Z≥0,on behalf of the node h= 1,h∈R1,to the nodes in R3.Figure5 shows the consequence of spoofing in the estimations.TheinitialestimatevaluesofthenodesinR2and R3remain constant for all the future time.It is noteworthy that,not only the nodes in R3are affected by the spoofing,but the nodes in R2are also affected indirectly and none of them can reach omniscience for z1.

While we primarily analyzed the success or failure of the network omniscience in the transformed dynamic system,the main results are valid for the original dynamic system with different time histories of state values(Figs.6 and 7).

6 Conclusions

Combining Byzantine adversarial model and spoofing as a misbehaving technique, we introduced a new type of cyber attack called smart spoofing. Then, we investigated the problem of distributed observer design for LTI systems in the presence of this attack which uses the asynchrony in communications to threaten the network. Using a two-step distributed mechanism,including a pre-executing algorithm for recognizing the trusted neighbors and a local-filtering algorithm for removing possible incorrect values induced by the adversarial nodes, the regular nodes can achieve resilient observation over so-called strongly robust graphs.We proposed resilient topology constraints on static and time-varying networks under the proposed adversarial threat.Numerical simulations with a sample network validate our analytic results.The proposed designs are applicable to a vast range of networked systems. In future studies, we consider resilient consensus problems prone to the smart spoofing attacks.

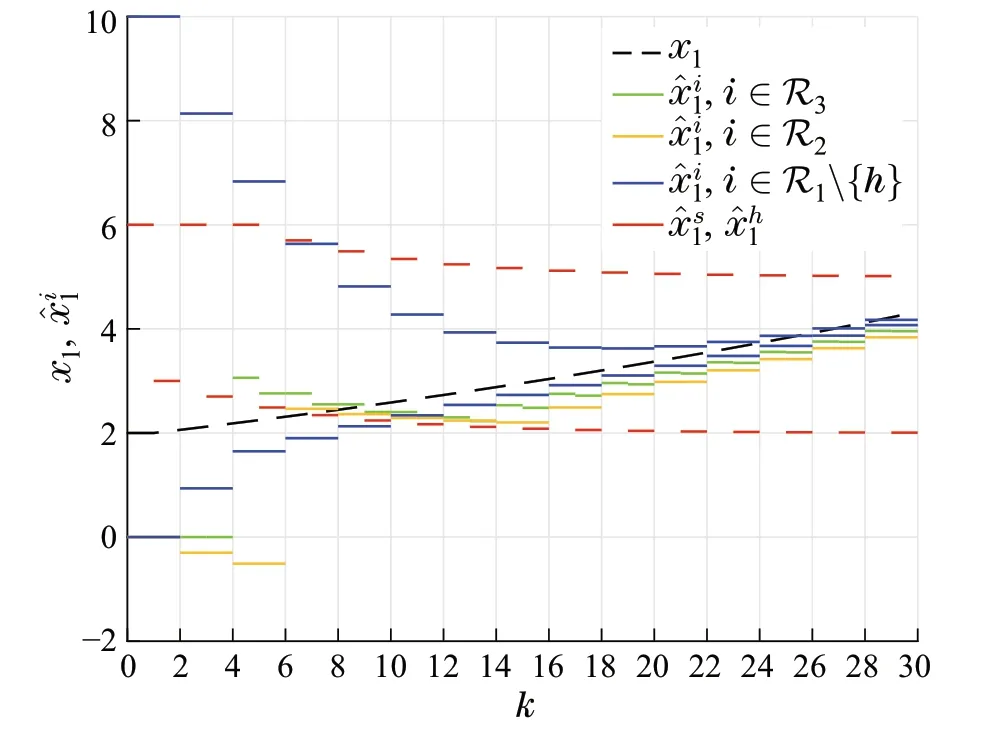
Fig.6 All the regular nodes truly estimate x1 while the smart spoofer s impersonates the node h ∈R1 for the nodes in R3

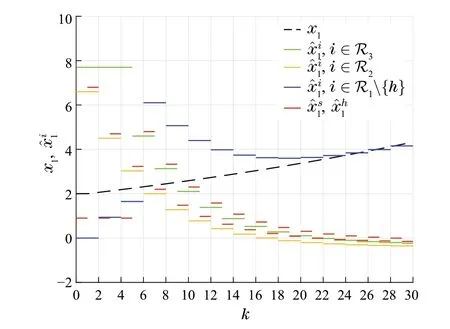
Fig.7 The regular nodes in R2 and R3 fail to estimate x1 if the smart spoofer s impersonates the node h ∈R1 for the nodes in R3

AcknowledgementsI offer my sincerest gratitude to Dr.Seyed Mehran Dibaji and Prof. Hideaki Ishii for the time they dedicated to me for useful discussions on the topic as well as their technical comments which significantly helped me to improve the quality of this paper.