Bipartite consensus for nonlinear time-delay multiagent systems via time-varying gain control method

Haiou Zhao·Yanan Qi·Yanjie Chang·Xianfu Zhang

Received:21 January 2022/Revised:16 May 2022/Accepted:8 June 2022/Published online:13 October 2022

©The Author(s),under exclusive licence to South China University of Technology and Academy of Mathematics and Systems Science,Chinese Academy of Sciences 2022

Abstract The bipartite consensus problem is addressed for a class of nonlinear time-delay multiagent systems in this paper.Therein,the uncertain nonlinear dynamics of all agents satisfy a Lipschitz growth condition with unknown constants,and part of the state information cannot be measured.In this case,a time-varying gain compensator is constructed,which only utilizes the output information of the follower and its neighbors.Subsequently,a distributed output feedback control protocol is proposed on the basis of the compensator.According to Lyapunov stability theory,it is proved that the bipartite consensus can be guaranteed by means of the designed control protocol.Different from the existing literature,this paper studies the leader–follower consensus problem under a weaker connectivity condition,i.e.,the signed directed graph is structurally balanced and contains a directed spanning tree.Two simulation examples are carried out to show the feasibility of the proposed control strategy.

Keywords Multiagent systems·Time-delay·Bipartite consensus·Time-varying gain·Output feedback

1 Introduction

Cooperative control of multiagent systems has attracted the attention of many scholars in the past few decades due to its broad application backgrounds,such as sensor networks,unmanned air vehicles,and industrial processes[1–3].Consensus control is a fundamental problem with high popularity in cooperative control [4]. It includes leaderless consensus and leader–follower consensus.One of the essential tasks of the leader–following consensus is to design distributed control protocols based on neighborhood information,such that the states of the followers track the states of the leader.Owing to the strong robustness and less communication requirements of distributed consensus protocols, many excellent strategies have been proposed from different perspectives for consensus control of multiagent systems. Single-integrator multiagent systems were studied in [5,6], multiagent systems for double integrator were investigated in [7,8], and high-order multiagent systems were considered in[9,10].

However,the above work only considers the cooperative relationship between agents, which implies that the entries in the adjacency matrix of the communication topology are nonnegative.In practical systems,cooperation and competition among agents may exist simultaneously.Based on this,the concept of the signed graph is proposed,where the positive and negative entries of its adjacency matrix represent the cooperation and competition interactions among agents,respectively.In addition,consensus control based on a signed topology is called bipartite consensus control.Bipartite consensus is that the agent converges to the corresponding value with the same module but for different signs. In [11], for the first-order multiagent systems, the bipartite consensus problem was introduced and studied for the first time. A time-delayed impulsive control strategy was proposed for second-order multiagent systems with switched topology to solve the bipartite consensus problem in [12]. In [13],the research of bipartite consensus was further extended to high-order multiagent systems.For general linear multiagent systems, state feedback and output feedback control were designed to achieve bipartite consensus in[14].

The time-varying gain control is an efficient method for handling leader–follower consensus problems in nonlinear multiagent systems. The prescribed finite-time consensus problem was handled by utilizing time-varying gain control methods for a class of uncertain second-order multiagent systems in [15]. For feedforward nonlinear multiagent systems,the leader–following consensus problem was solved by designing output feedback controllers with a time-varying gain in [16]. In [17], using the time-varying gain control approach,the leader–follower consensus problem of nonlinear multiagent systems was transformed into the construction of a time-varying function. For a class of nonlinear timedelay multiagent systems,the consensus problem was solved by designing a time-varying gain in[18].A time-varying gain control technique is used to handle the influence of unknown constants and realize the consensus of multiagent systems in[19].For feedforward nonlinear time-delay multiagent systems, a static low-gain controller and a time-varying gain method were proposed in[20],which showed that the latter improved the convergence speed and transient performance of the distributed consensus protocol.As one of the sources of destroying system stability and reducing system performance, time-delay often appears in practical systems [21].Many works considered the existence of time-delays in nonlinear multiagent systems[5,18,20,22,23].However,as far as we know,little attention has been focused on using the timevarying gain control method to solve the bipartite consensus problem of nonlinear time-delay multiagent systems.

In this paper, the bipartite consensus of nonlinear timedelay multiagent systems is addressed using the time-varying gain control method. Compared with the existing results,the contributions of this paper can be summarized as follows. First, with the help of the time-varying gain method,a bipartite consensus protocol is constructed for a class of uncertain nonlinear multiagent systems, which satisfy a Lipschitz growth condition with unknown constants. Specially, the time-varying gain effectively handles the effects of unknown constants. Second, different from the work in[17–20],where only cooperative interaction exists,this paper considers a more realistic situation, that is, some agents in the investigated graph may cooperate, while others may compete. Third, it is worth noting that the proposed control strategy shows great advantages in energy saving and flexible implementation. Specifically, since only the output information of the follower and its neighbors is utilized,the developed protocol economizes the communication bandwidth compared with[17].

The remainder of this paper is organized as follows.Section 2 describes the preliminary knowledge and problem description. Section 3 introduces the design of the control protocol.Two simulation examples are presented in Sect.4 to prove the effectiveness of the control strategy. The conclusion and future outlook are drawn in Sect.5.

2 Preliminaries and problem formulation

2.1 Topology theory

If there is a directed path{(k,k1),(k1,k2),...,(kl,i)}⊆Ebetweeniandk, the agentiis reachable from the agentk.Gis said to be strongly connected if there are directed paths for any two agents. The signed topologyGis called structurally balanced,if there are two subsetsVp,p= 1,2 that satisfyV=V1∪V2,V1∩V2= ∅,aik≥0 for alli,k∈Vp(p= 1,2),andaik≤0 fori∈Vp,k∈Vqwithp/=q(p,q=1,2).

An augmented signed topology ¯G={G∪0∪ES(i,0)} is employed to describe the communication between a leader numbered 0 andNfollowers indexed by 1,2,...,N,where ES(i,0) denotes a set of edges connecting leader 0 and followeri. A pinning matrix is defined asB=diag{b1,b2,...,bN},wherebi=1 if the agentican acquire the information of the leader andbi=0 otherwise.An augmented matrix is represented as ¯L=L+B.

Assumption 1The signed topologyGis structurally balanced and contains a directed spanning tree.

Lemma 1[24]Define the gauge transformation set Q:={diag{σ1,σ2,...,σN}∈ {±1},i∈V}.If the signed topology G is structurally balanced,there must be a matrix Q∈Q satisfying the entries of QAQ are nonnegative,i.e.,Define a matrix as.

2.2 System formulation

ConsiderN+ 1 agents given in the topology theory. The agenti,i=0,1,...,Nare modeled as

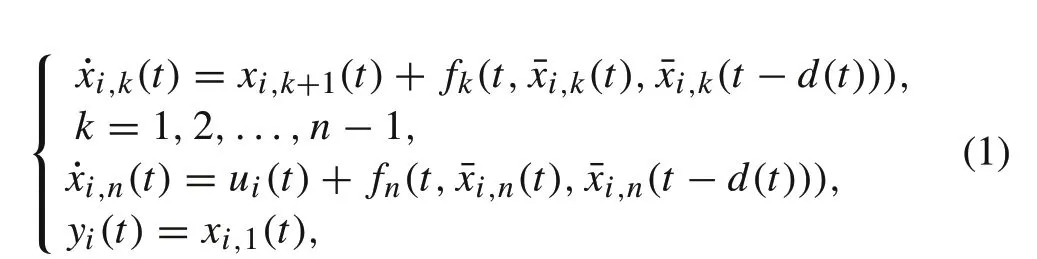
wherexi,k(t) ∈R,ui(t) ∈R andyi(t) ∈R are the state,input, and output of theith agent, respectively,u0(t) = 0,i,k(t) = [xi,1(t),xi,2(t),...,xi,k(t)]T,i,k(t−d(t)) =[xi,1(t−d(t)),xi,2(t−d(t)),...,xi,k(t−d(t))]T,the timedelayd(t) satisfies 0 ≤d(t) ≤d∗and its derivative ˙d(t)satisfies ˙d(t) ≤≤1, in whichd∗andare known constants,only the output is measured,andfk(·) : R+×Rk×Rk→R is an uncertain continuous function satisfies the following Lipschitz condition.

Assumption 2For any(t, ¯xi,k, ¯xi,k,d) ∈R+× Rk× Rk,k=1,2,...,n,the following condition holds:

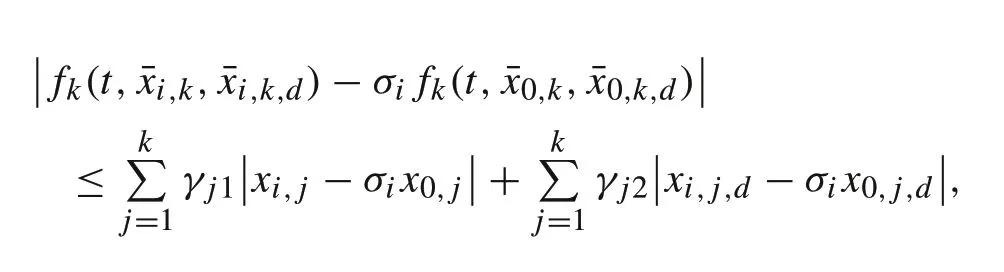
whereγ j1 andγ j2 are unknown nonnegative constants,xi,k,d=xi,k(t−d(t))andi,k,d=i,k(t−d(t)).

Lemma 2[22]For functions f≥0,g≥0,the following inequality holds:

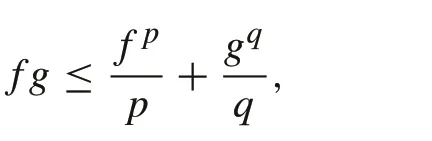
Remark 1Assumption 1 and signed topology theory are the basic assumptions for realizing bipartite consensus[24,25].Assumption 2 shows that nonlinear functions satisfy a Lipschitz condition with unknown constants. The nonlinear function satisfies the same form for each follower, which is a crucial assumption to realize the consensus.Compared with[18]and[19],the assumptions in this paper are further relaxed. Many practical projects can be modeled as system(1), such as chemical reactor systems [19] and pendulum systems[24].

3 Output feedback controller design

In this section, the bipartite consensus problem for system(1)is studied. For theith agent, the output consensus error is defined as

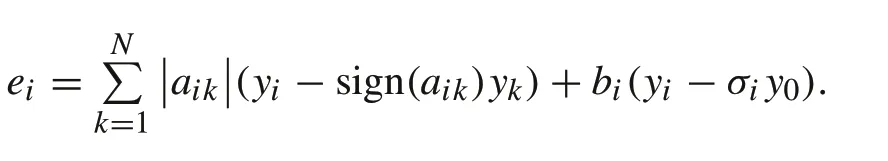
Sinceonlythesystemoutputismeasurable,acompensator for agentican be modeled as

one obtains

The output feedback controllers are designed as

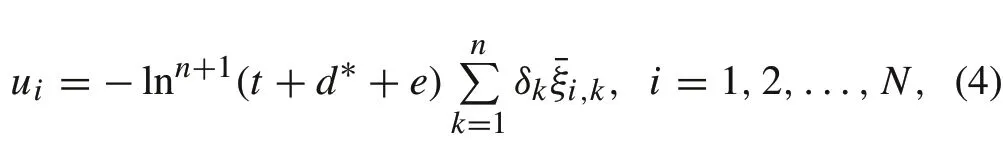
whereδk,k= 1,2,...,nare the parameters to be selected later.

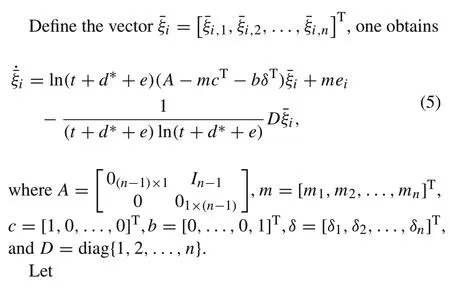
ηi,k=xi,k−σi x0,k−ξi,k,k=1,2,...,n,

and one obtains

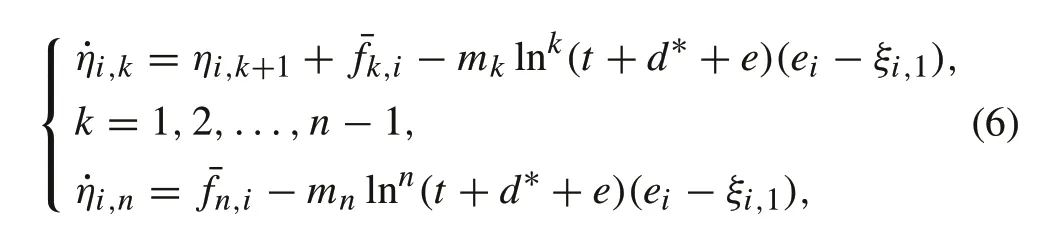
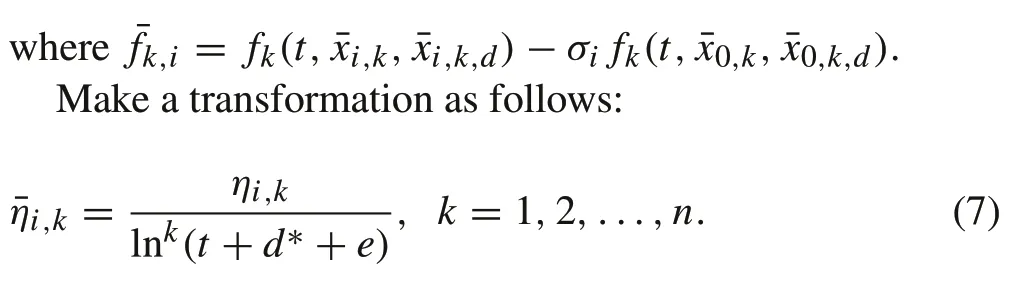
From(6)and(7),one has

Remark 2The compensator (2) only uses the output information of followers and their neighbors. Therefore, the computational burden of the algorithm is reduced. The distributed output feedback controllers(4)only call the corresponding compensator.The controllers reduce information transmissionandsavecommunicationbandwidth.Theconditions imposed on nonlinear terms are further relaxed,and the dynamic gain controller proposed in[18]cannot effectively address the consensus problem of system (1). To solve the influence of unknown constantsγ j1andγ j2,j=1,2,...,n,the time-varying gain with the logarithmic form is constructed.Moreover,the controller has a simple structure that can easily be implemented in practice.

Theorem 1Under a signed topology G,consider the multiagent system satisfying Assumptions1and2.The distributed output feedback controllers(4)are constructed such that the bipartite consensus of system(1)is achieved.

ProofAccording to Lemmas 2 and 3 in [18] and Theorems 1–3 in [26],is a Hurwitz matrix by selecting appropriate vectorsmandδ. Therefore, there must be two positive constantsμandι0, positive definite matrixP=diag{P1,P2,...,PN},Pi∈R2n×2n,i= 1,2,...,Nsatisfying

Choose a candidate Lyapunov function asV1=ΨTPΨ,its derivative along(11)is

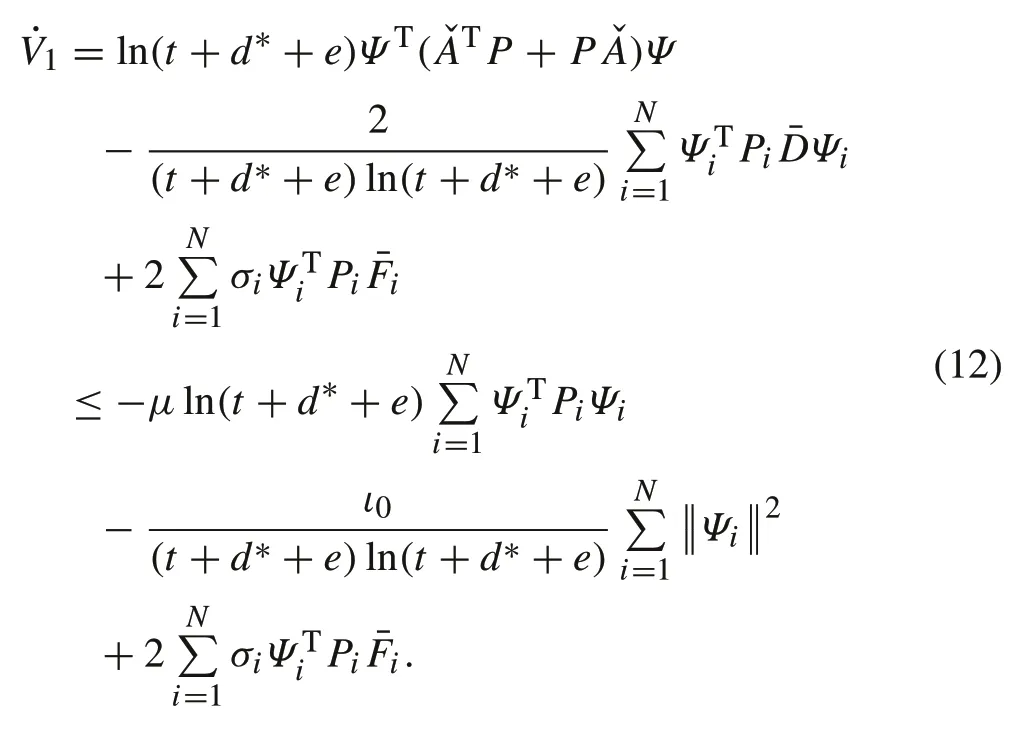
Based on Assumption 2,one obtains

whereξi,k,d=ξi,k(t−d(t)),andηi,k,d=ηi,k(t−d(t)).

Based on the definitions ofi,k, ¯ηi,k,i,kandi,k,it can be further obtained that

It follows from(14)and Lemma 2 that:

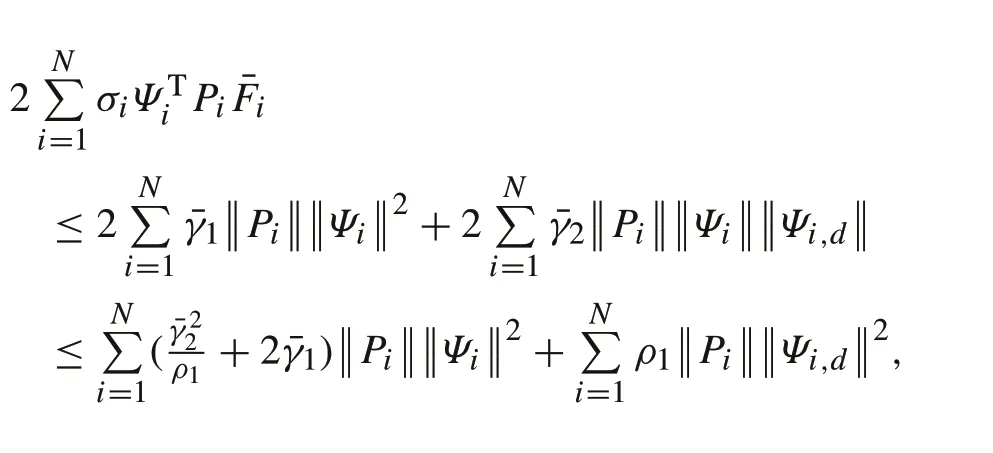
whereρ1is a positive constant.Therefore,one obtains

Choose a candidate function as

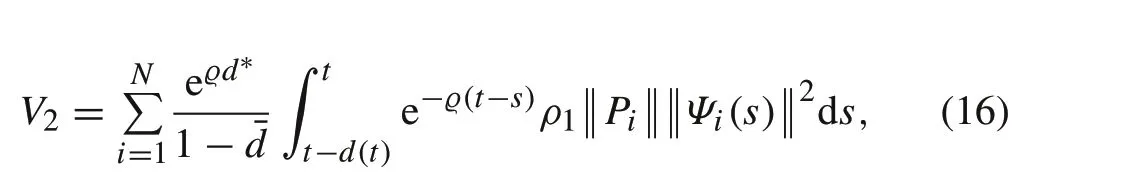
whereϱis a positive constant. Then, its time derivative is calculated as

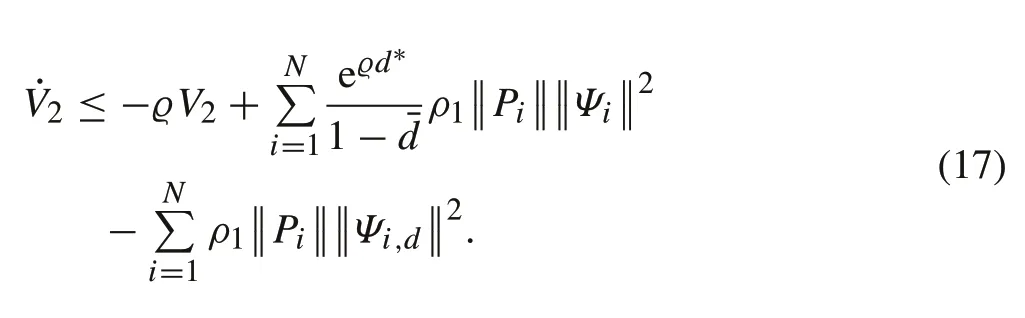
Based on the discussions above, a function designed asV=V1+V2.The derivative ofVsatisfies

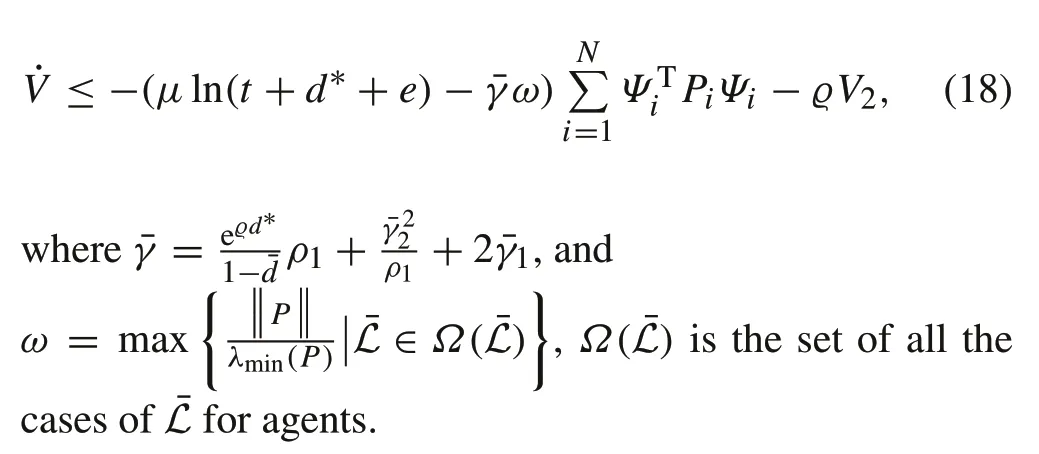
Therefore, there exists a positive constantκand a finite timet1satisfyingμln(t+d∗+e)−¯γ ω>κ,t∈[t1,+∞)and

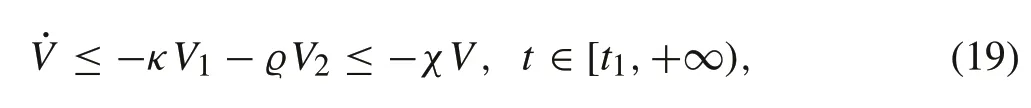
whereχ=min{κ,ϱ}.

Based on(19),one obtains

V(t)≤V(t1)e−χ(t−t1),

which means thatV1=ΨTPΨ≤V(t1)e−χ(t−t1)ont∈[t1,+∞).

Then,one has

Fort∈[t1,+∞),the following inequality holds:

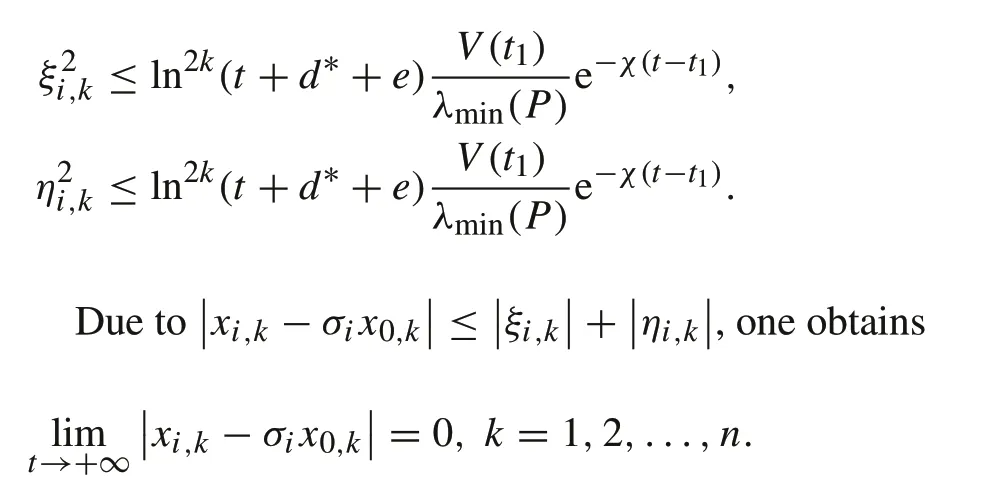
The proof of Theorem 1 is completed. ■

ThroughtheaboveanalysisandcombinedwithL’Hopital’s rule,although the time-varying gain lnk(t+d∗+e)tends to infinity when timettends to infinity,ξi,kandηi,kconverge to 0.It further shows that the bipartite consensus of system(1)is completed.In addition

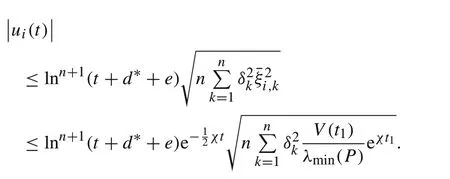
Remark 3The study of multiagent systems with cooperative andantagonisticinteractionsisofnotonlytheoreticalbutalso practical importance.Examples of bilateral monopoly structures, two-party political systems, and social networks are practical applications of bipartite consensus. Conventional consensus can be regarded as a particular case of bipartite consensus. The control strategy proposed in this paper can also be applied to the conventional consensus,expanding the scope of application.

4 Simulation examples

To illustrate the feasibility of the proposed control strategy,two simulation examples are given.

4.1 Example I

It follows from[18]that the two-stage chemical reactors with delayed recycle streams as agents can be modeled as

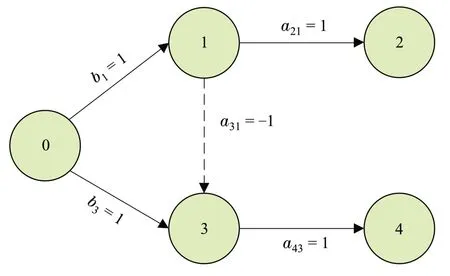
Fig.1 Topology of augmented graph ¯G

wherexi,1andxi,2are compositions,θi,1andθi,2denote the reactor residence times,βi,1andβi,1are reaction constants,ri,1andri,2denote the recycle flow rates,νi,1andνi,2are reactor volumes,αi,2is the feed rate,w1(·)andw2(·)denote the nonlinear functions describing the system uncertainties and external disturbances, andd(t) = 0.6+0.2 sintwithd∗= 0.8 and ¯d= 0.2. The topology is provided in Fig.1.Takeθi,1=θi,2= 10,βi,1= 0.02,βi,2= 0.05,ri,1=ri,2 = 0.2,νi,1=νi,2= 0.8,αi,2= 0.8,w1(·) =0.03xi,1,w2(·) = 0.25xi,2,d. It is clear that system (21)satisfies Assumption 2. Choose vectors asm= [2,1]T,δ=[14,3]T.

Then, the compensator for followeri,i= 1,2,3,4 are designed as follows:

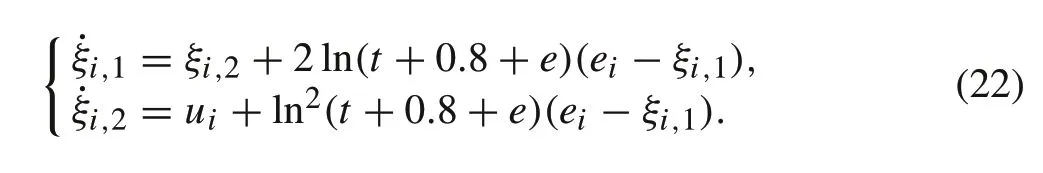
Based on the compensator (22), construct the controller for followeri,i=1,2,3,4 as

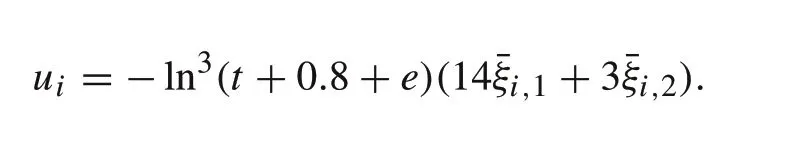
Without loss of generality,the initial conditions of agents are chosen randomly. The initial values are selected asxT0= [−0.5,1],xT1= [−0.3,12],xT2= [−0.6,−15],xT3= [0.4,−5],xT4= [−0.2,10],ξT1= [−0.4,0.1],ξT2= [0.1,−0.2],ξT3= [0.1,0.3],ξT4= [−0.2,0.1] ont∈[−0.8,0].

Figures2, 3, 4 show the simulation results of Example I. The output trajectories and reference signal are depicted in Fig.2. The trajectoriesxi,2and control inputsui,i=0,1,...,4aredepictedinFigs.3and4,respectively.According to the results in Figs.2,3,4,the control strategy proposed in this paper enables system(21)to achieve bipartite consensus,which is consistent with Theorem 1.

In contrast to the simulation example in [18], the timevarying gain controller with a logarithmic function proposed in this paper has a lower gain,and the response of the controller does not undergo abrupt changes. In addition, the control strategy proposed in this paper can simultaneously solve the conventional consensus problem of the simulation example in[18]and deal with the bipartite consensus problem.

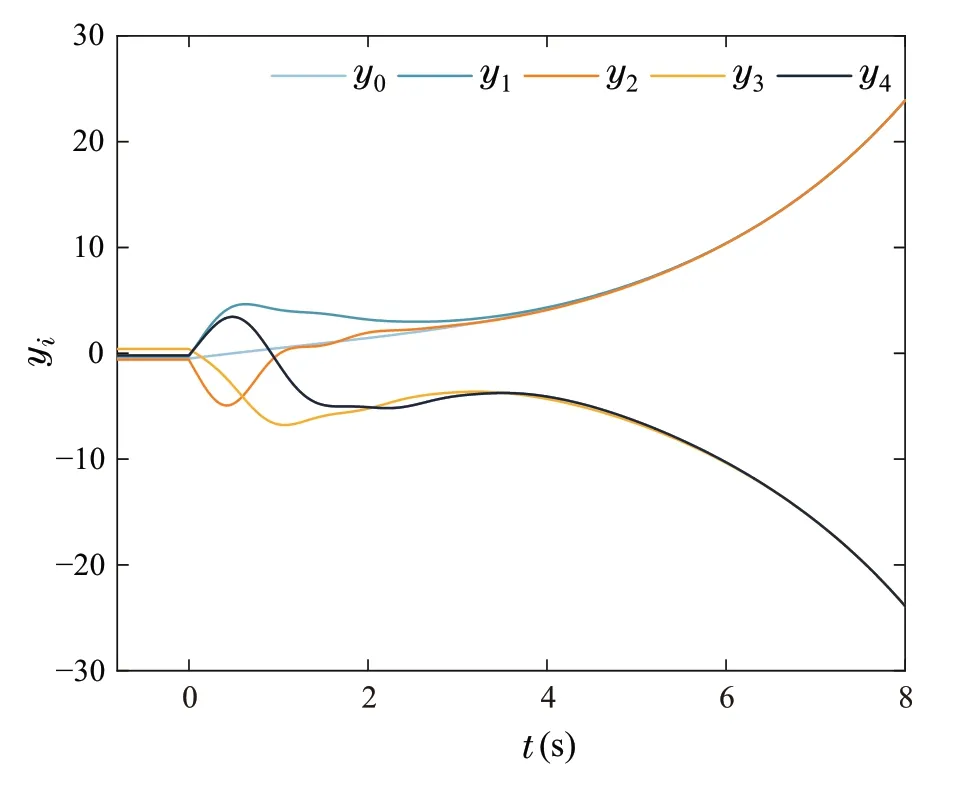
Fig.2 The responses of yi,i =0,1,2,3,4

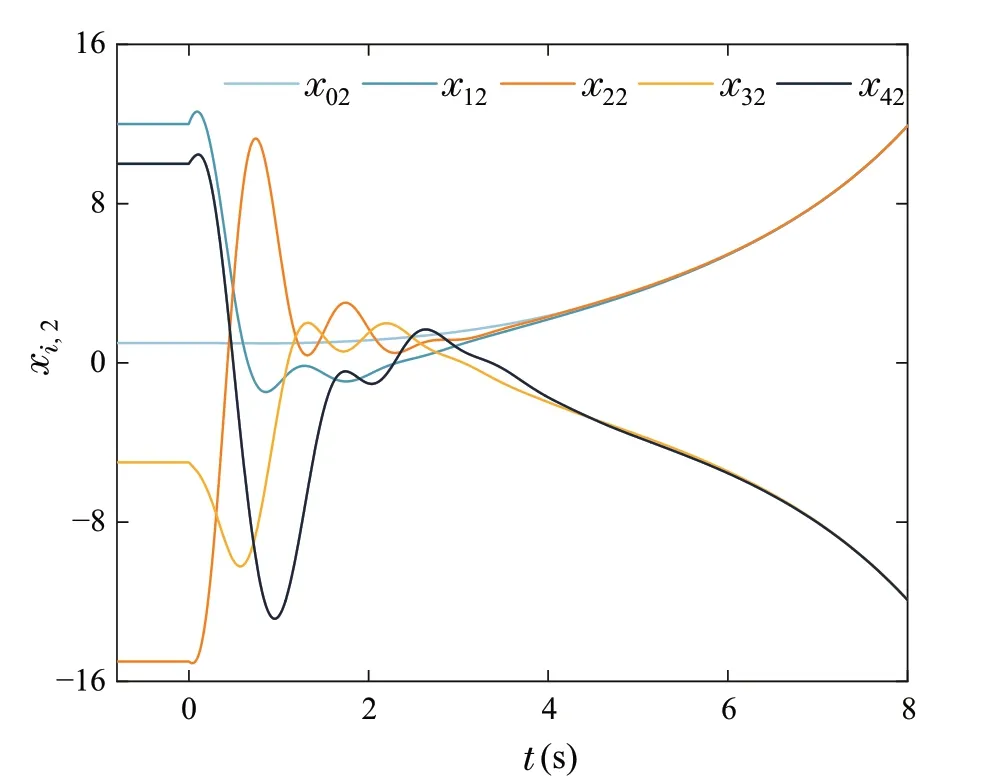
Fig.3 The responses of xi,2,i =0,1,2,3,4

4.2 Example II

Consider a multiagent system composed of a leader and four followers,and the dynamics can be described as

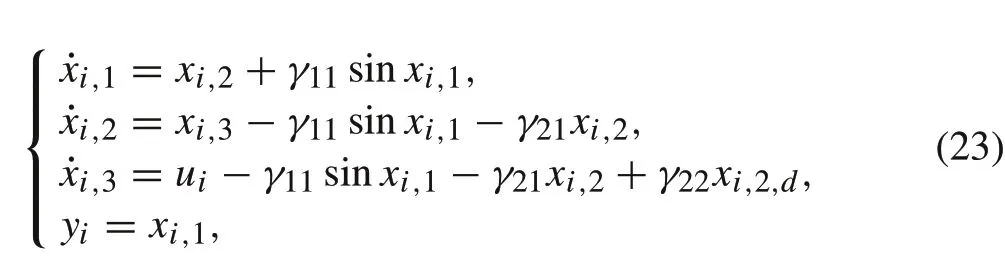
whereγ11,γ21andγ22are unknown positive constant, andd(t) = 0.6 + 0.2 sintwithd∗= 0.8 and ¯d= 0.2.The topology is provided in Fig.1. It can be noted that its dynamics satisfy Assumption 2 withf1(t,i,1,i,1,d) =γ11 sinxi,1,f2(t,i,2,i,2,d) = −γ11sinxi,1−γ21xi,2,andf3(t, ¯xi,3, ¯xi,3,d) = −γ11sinxi,1−γ21xi,2+γ22xi,2,d.Choose vectors asm=[0.85,0.4,0.1]Tandδ=[23.5,18,11.5]T.

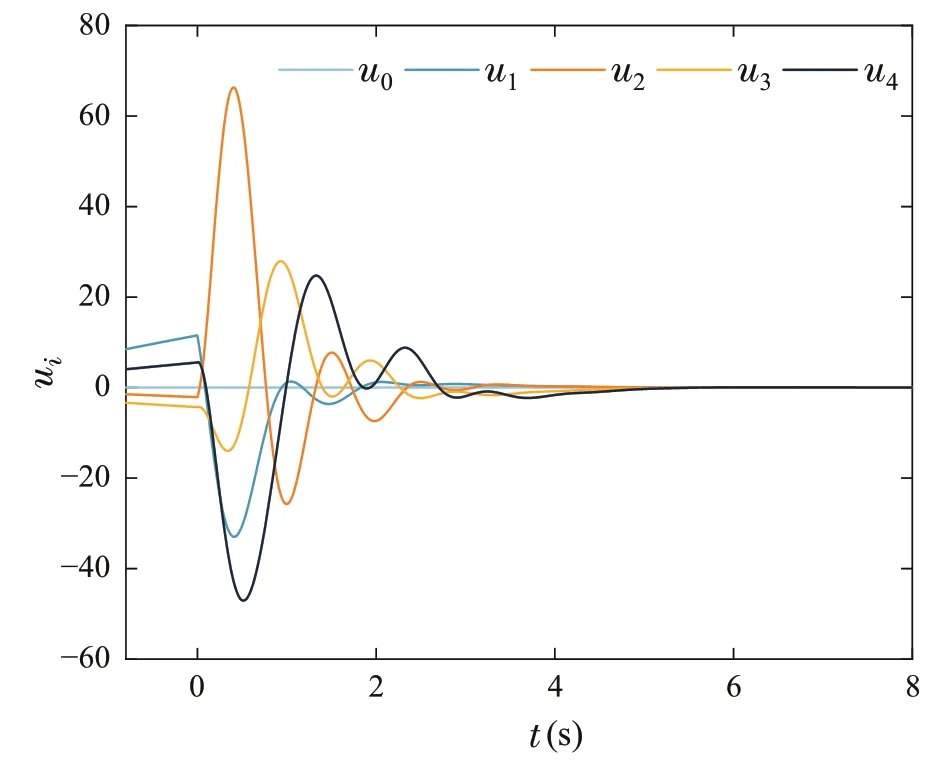
Fig.4 The responses of ui,i =0,1,2,3,4

Then, the compensator for followeri,i= 1,2,3,4 are designed as follows:

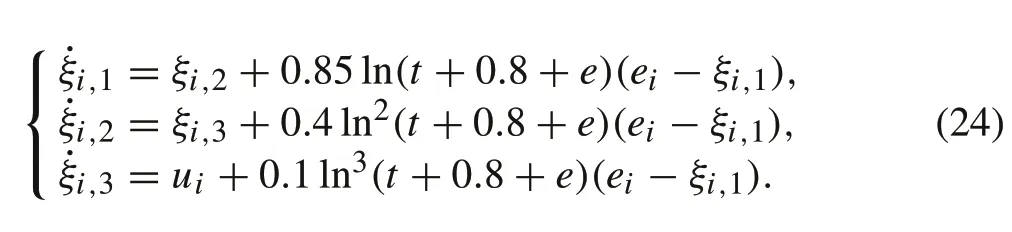
Based on the compensator (24), construct the controller for followeri,i=1,2,3,4 as

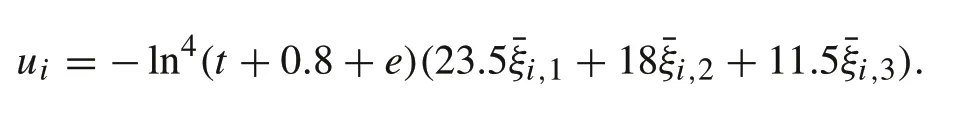
TheinitialvaluesareselectedasxT0=[1,0.55,0.4],xT1=[0.5,0.1,0.5],xT2= [0.3,0.7,0.7],xT3= [1.6,0.1,0.3],xT4= [0.8,1.2,1],ξT1= [2,0.5,0.2],ξT2= [1.5,0.5,1.1],ξT3=[0.7,1,0.4],ξT4=[1,0.3,0.8]ont∈[−0.8,0].

Figures5,6,7,8showthesimulationresultsofExampleII.In Fig.5,the time responses of the output and reference signal are presented.The trajectoriesxi,2andxi,3,i=0,1,2,3,4 are shown in Figs.6 and 7,respectively.Profiles of the control signals are described in Fig.8.In the light of Figs.5,6,7,8,it can be concluded that the control strategy proposed in this paper achieves the bipartite consensus of system(23).

5 Conclusions

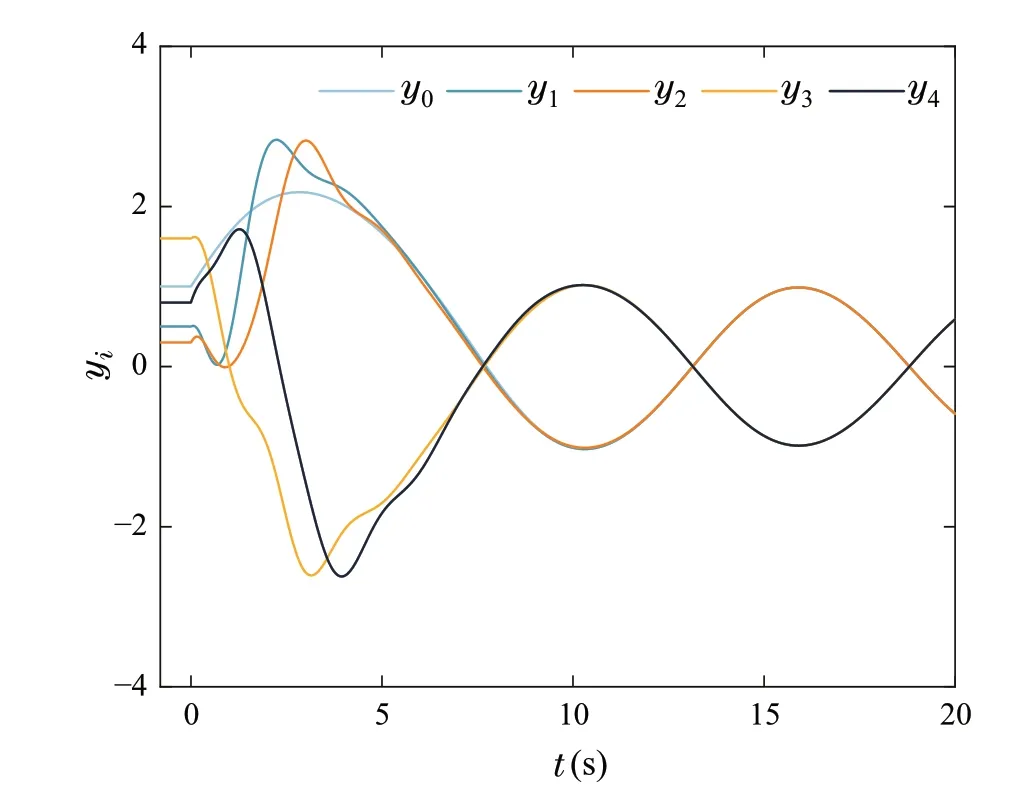
Fig.5 The responses of yi,i =0,1,2,3,4

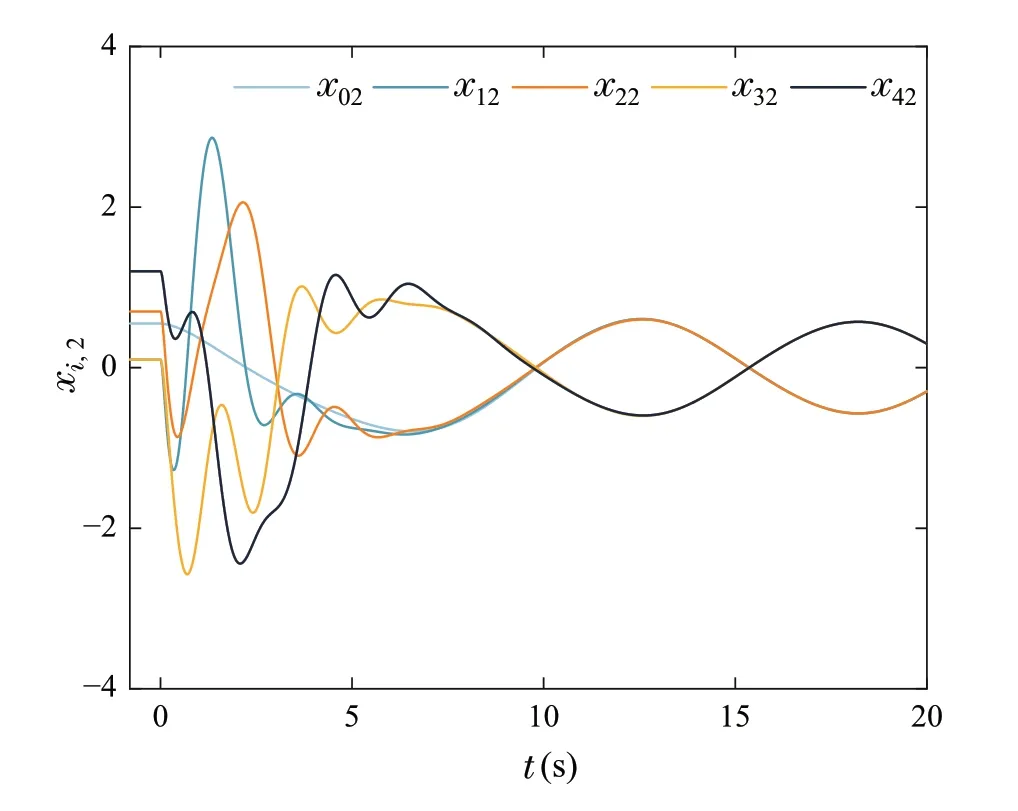
Fig.6 The responses of xi,2,i =0,1,2,3,4

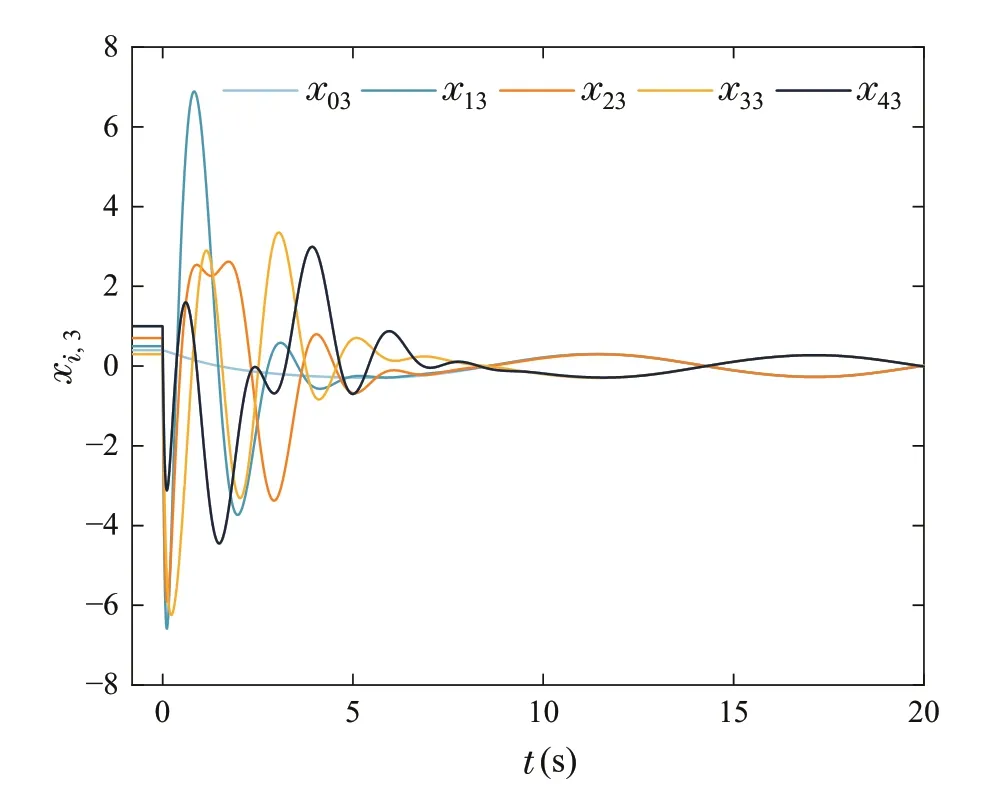
Fig.7 The responses of xi,3,i =0,1,2,3,4

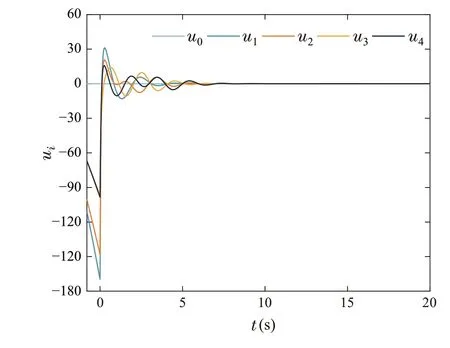
Fig.8 The responses of ui,i =0,1,2,3,4

In this paper,the bipartite consensus problem has been solved for a class of nonlinear time-delay multiagent systems in directedcommunicationnetworks withcooperativeandcompetitive interactions. According to the output information of each agent, we have designed a time-varying compensator to estimate the tracking error between the follower and the leader.Then,based on the adjacency matrix of a signed directed graph, a consensus protocol has been designed to guarantee that all agents achieve consensus with the same value but opposite sign. Finally, two simulation examples have been provided to show the effectiveness of the control strategy. A possible future work is to extend the algorithm to nonlinear time-delay multiagent systems with faults or attacks.