Design of semi-tensor product-based kernel function for SVM nonlinear classification

Shengli Xue·Lijun Zhang·Zeyu Zhu

Received:7 June 2022/Revised:4 August 2022/Accepted:16 September 2022/Published online:28 November 2022

©The Author(s),under exclusive licence to South China University of Technology and Academy of Mathematics and Systems Science,Chinese Academy of Sciences 2022,corrected publication 2022

Abstract The kernel function method in support vector machine(SVM)is an excellent tool for nonlinear classification.How to design a kernel function is difficult for an SVM nonlinear classification problem,even for the polynomial kernel function.In this paper,we propose a new kind of polynomial kernel functions,called semi-tensor product kernel(STP-kernel),for an SVM nonlinear classification problem by semi-tensor product of matrix(STP)theory.We have shown the existence of the STP-kernel function and verified that it is just a polynomial kernel. In addition, we have shown the existence of the reproducing kernel Hilbert space(RKHS)associated with the STP-kernel function.Compared to the existing methods,it is much easier to construct the nonlinear feature mapping for an SVM nonlinear classification problem via an STP operator.

Keywords SVM·Semi-tensor product·STP-kernel·Nonlinear classification·Reproducing kernel Hilbert space(RKHS)

1 Introduction

Binary classification has made a basic and crucial impact in pattern recognition and machine learning field.Support vector machine(SVM)was proposed in the late 1990s in[1]and has been successfully applied in many fields[2–9].Given a data set, the classical linear SVM model uses a hyperplane to divide the data points into two classes,while maximizing the margin between the two classes and minimizing the misclassification of data points. Accordingly, nonlinear SVM model borrows the idea of linear classification model to first transform the nonlinear classification problem into a linear separable problem by a feature mapping[10],and then design a linear hyperplane to separate two sets of the mapped points in the feature space using the linear classification technique.How to design nonlinear kernel functions in SVM classification problem is a key point.A proper kernel function can largely reduce the computation cost and simplify the nonlinear classification problem to a linear counterpart in a higher dimensional feature space. The polynomial kernel and the Gaussian kernel,etc.,are widely applied to nonlinear classification problems.So far,there have ever been no common and useful methods for constructing the kernel functions,even polynomial kernel functions.Therefore,we attempt to design an algorithm for the SVM polynomial kernel function based on semi-tensor product of matrices theory.

The semi-tensor product(STP)of matrices,proposed by Cheng in[11],is a generalization of the conventional matrix product and well defined for arbitrary two finite-dimensional matrices.STP has been applied to control theory[12],image compression[13],game theory[14]and logic reasoning[15].Recently,Cheng[16]used STP technique to transform multivariable polynomial into a linear structure form similar to single variable polynomial [16]. As a result, any homogeneous polynomial can be expressed as a power function under the frame of STP.That is,in the higher dimension space generated by STP operator,the homogeneous polynomial is of linear-like form(Refer to[16]for details).

Motivated by STP representation of multivariable polynomial in [16], in this paper, we propose a new kind of polynomial kernel functions, denoted by the STP-kernel,for nonlinear SVM model via a semi-tensor product. The proposed STP-kernel technique can produce the well-known polynomial kernel.Based on that,we study the existence of the STP-kernel and show the STP-kernel is also a Mercer’s kernel.Then,the reproducing kernel Hilbert space(RKHS)associated with the STP-kernel is investigated, and some interesting properties are obtained.Numerical examples are taken to illustrate the effectiveness and efficiency of the proposed STP-kernel function.

The rest of the paper is organized as follows.In Sect.2,we introduce some preliminary knowledge about semi-tensor product and SVM-based binary classification.In Sect.3,we define the STP-kernel function and show that it is a Mercer’s kernel.In Sect.4,we show that STP-kernel is a generalization of polynomial kernel.RKHS associated with STP-kernel is investigated in Sect.5.Section 6 concludes the paper.

2 Preliminaries

In this section, we introduce some preliminary knowledge about semi-tensor product and SVM-based nonlinear binary classification. For the symbols and notions of semi-tensor product in this paper,refer to[16].

2.1 Semi-tensor product

Definition1 [16]LetA∈Mm×n,B∈Mp×qandt=n∨pbe the least common multiple ofnandp.Then,the left STP ofAandB,denoted byA×B,is defined as

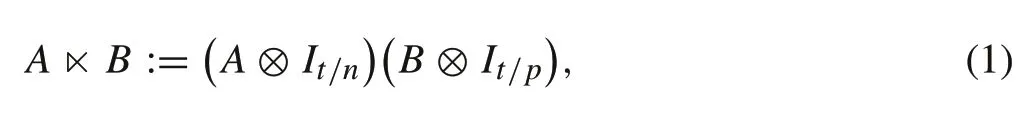
where ⊗is the Kronecker product.

Proposition 1[16]Let x∈Rm and y∈Rn be two column vectors.Then,x×y is well defined.Moreover,

x×y=x⊗y.

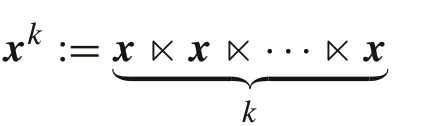
is always well defined.

From Proposition 2, STP can be regarded as an operator from a lower dimensional space to a higher dimensional space.

Definition 2Letx∈Rnbe a column vector,2 ≤k∈N+.Then,the STP operator×kis defined as follows:

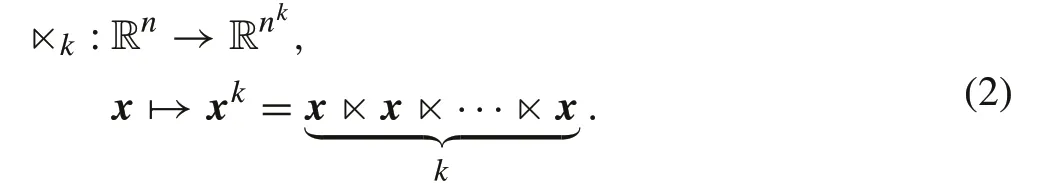
Remark 1

(1) It is easy to verify that ×k(ax) =a2×k(x), for allx∈Rn,a∈R,that is to say,the STP operator×kis a nonlinear operator.

(2) In the following text,we will sometimes useφ(x)=xkto represent×k(x)=xk.

By Proposition 2,letx=(x1,···,xn)T,it is easy to see that the components ofxkform a set ofkth degree homogeneous polynomials, denoted by, and define= R as zero-degree polynomials,i.e.,constants.Letf(x) ∈there exists a matrixF∈M1×nksuch that

Notexkis not a basis ofue to containing some redundant elements.That is,matrixFin(3)is not unique.

A basis of,called the natural basis and denoted byis defined as

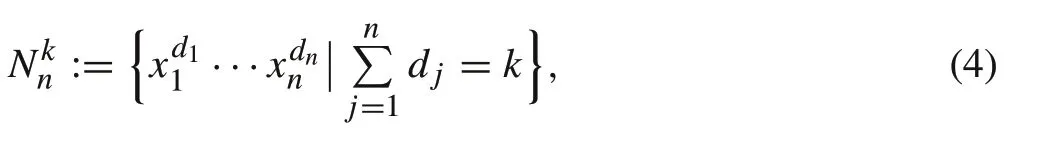
where 0 ≤d1≤d2≤···≤dn≤k,d j∈N.

Proposition 3[16]The cardinality(size)of Nkn is

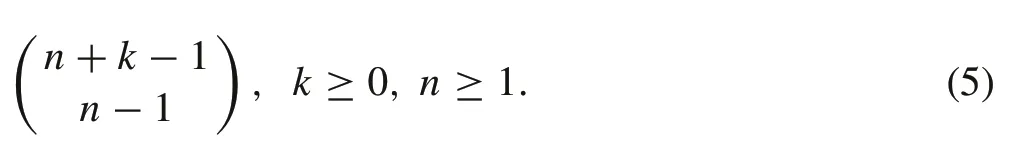
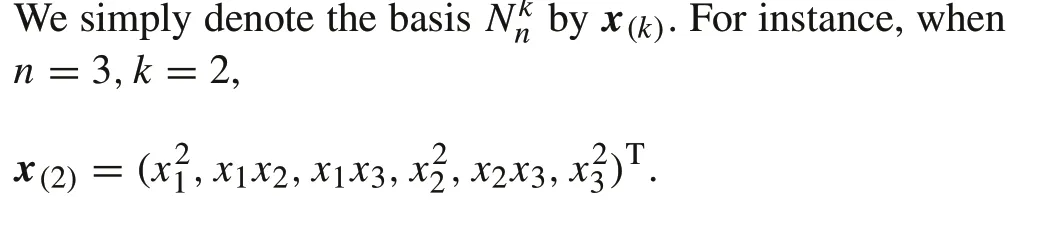
Next, we introduce how to represent the coefficient of a homogeneous polynomials inby a natural basisand vice versa.

Define matricesTB(n,k) ∈Ms×t,TN(n,k) ∈Mt×s,we have the following result(for details,please refer to[16,pp.440–441]):

Proposition 4[16]

2.Assume p(x) ∈is a kth degree homogeneous polynomial,and p(x)=Fxk=Sx(k),then

Example 1[16]Letn=2 andk=3.

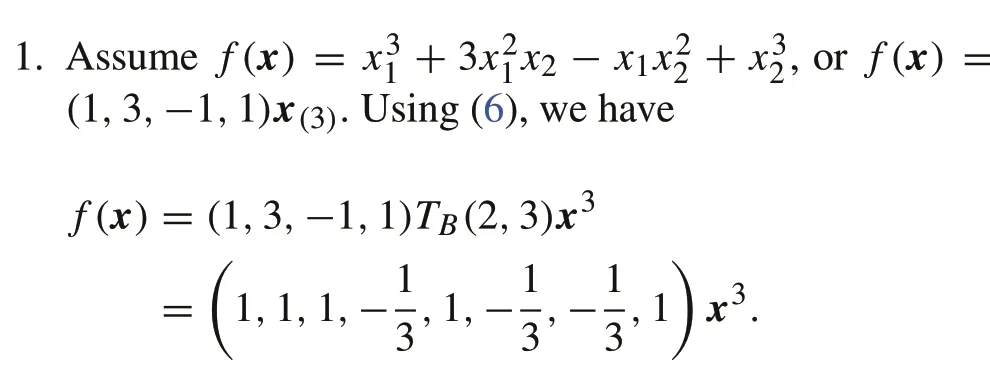
2. Assumef(x) =(1,2,1,1,−1,−1,−2,−1)x3.Using(6),we have

f(x)=(1,2,−2,−1)x(3).

2.2 SVM-based nonlinear binary classification

Given a data set of two classes as follows[17]:

The nonlinear classification task could be done by an SVM model with a kernel function[10],which is obtained by the following optimization model:

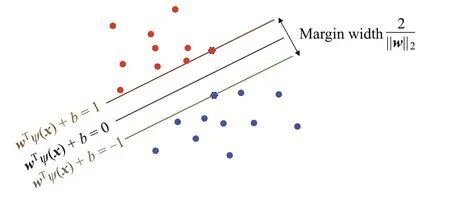
Fig. 1 The hyperplane f(x) = wTψ(x)+b of SVM in the feature space

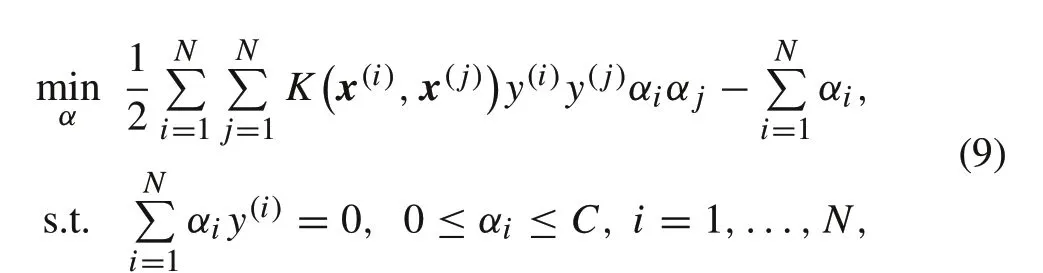
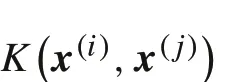
2.3 Positive definite kernel and RKHS

Definition 3 LetXbe an abstract set.We say thatK:X×X→R is symmetric whenK(x,t)=K(t,x)for allx,t∈X.

For the kernelKdefined onX×X,x∈X, we denote byKxthe function

Then, the following theorem describes the conditions for RKHS.

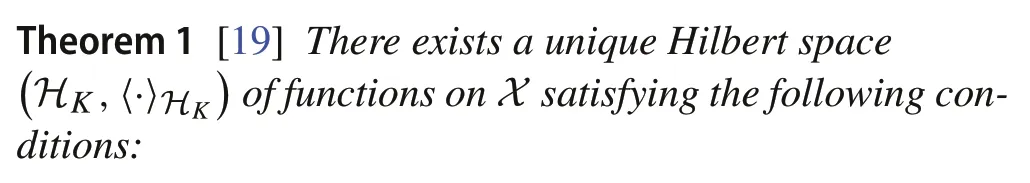
(1)for all x∈X,Kx∈HK,

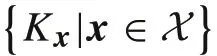
(3)for all f∈HK and x∈X,f(x)=〈Kx,f〉HK.

By Theorem 1,the Hilbert spaceHKis said to be aRKHS.The kernelKis said to bereproducing kernel.Property(3)in Theorem 1 is referred to as thereproducing propertyof the reproducing kernel.

Lemma 1[19]A RKHS of functions on X is characterized by its kernel K on X×X,then it is equivalent that K is a reproducing kernel and that K is a positive definite kernel.

Remark 2[20]Commonly,a positive definite kernel is calledMercer kernelor reproducing kernel.

From (8) and (9), we note that the kernel technique is a key point to solve the nonlinear classification problem, the choice of kernel function will determine whether a hyperplane separating the data in the feature space exists.So far,some widely used kernel functions are Gaussian(RBF)kernel and quadratic(2nd order polynomial)kernel,etc.

Here,we give two examples of kernel functions as follows.

We knowK(x,y) = 〈x,y〉is the well-known homogeneous polynomial kernel.

Example 3(Non-homogeneous polynomial kernel)LetX⊂Rn,a> 0,d∈N+,the non-homogeneous polynomial kernel is

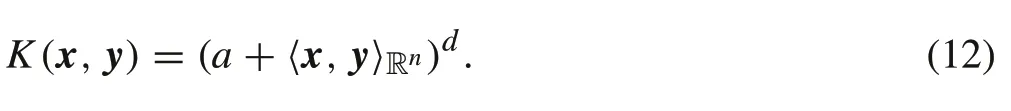
Leta= 0,it is simplified as a homogeneous polynomial kernel.

3 STP representation of polynomial kernel function

In this section, we claim that a polynomial kernel can be expressed as a form of semi-tensor product of a matrix. In fact,Cheng in[11]proposed that a multivariable polynomial can be expressed as a linear structure form similar to a single variable polynomial, which motivates us to construct STPbased polynomial kernel with linear structure in the higher dimension space.Here,we will use an example to verify our idea. For example, we assume the following homogeneous polynomialψ(x)is a nonlinear separable function in a given data space.

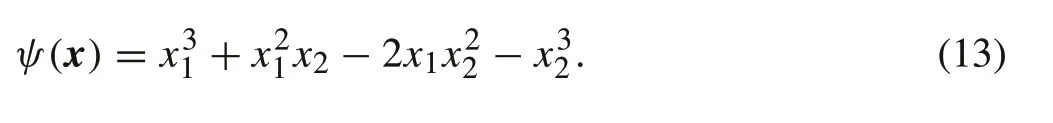
Its corresponding STP representation can be written as

whereA=(1,1,0,−2,0,0,0,−1)is a row vector,andx3is

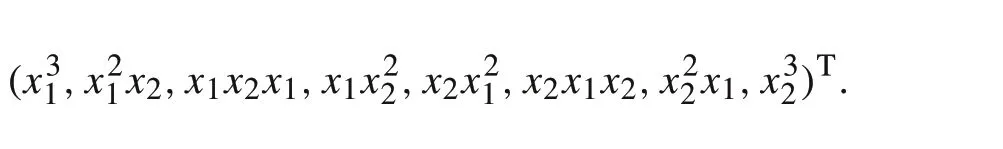
We note that(13),a nonlinear function in R2,is converted into a linear formψ(x) =Ax3in R8.In other words,from the perspective of SVM nonlinear binary classification, the STP operator ×3in Definition 2 can transform a nonlinear classifier(13)in the data space R2into a linear classifier(14)in a high dimension of feature space R8.

Motivated by the above example, we proceed to investigate the following common known example in SVM classification theory[1].

Figure 2 shows us how a nonlinear classification problem in R2is transformed into a linear classification problem in R3by a feature mapping as follows:

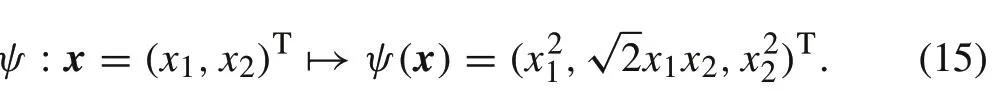
Then, the corresponding kernel function with respect toψ(·)is written as follows:

Now,we define a feature mappingφ(x)∈R4by the STP operator as follows:

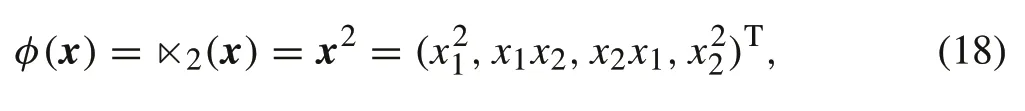
and the corresponding kernel function is written as

We note that (17) is identical to (20), i.e.,K(x,y) =K′(x,y).It implies semi-tensor product(18)can also specify the feature mapping(15)and construct a new kind of kernel function. One can also see that the feature mapping is not unique for a given kernel function. However, in practice, it is not easy to construct the feature mapping for a nonlinear classification problem.So far,even for the polynomial kernel,how to construct the feature mappingψorφof the kernelK(x,y)is unknown.Clearly STP provides a new approach to constructing the polynomial kernel function from the data space.In the sequel,we will investigate how STP generates a polynomial kernel function in theory.

4 STP-kernel generates polynomial kernel

In this section, we show that the nonlinear function based on STP is just a kernel function in SVM theory,called STPkernel.

Next,we will give the definition and criteria of the STPkernel.

Theorem 2STP-kernel

K(x,y)=〈φ(x),φ(y)〉Rnk

is apositivedefinitekernel,aMercer kernel,andalsoareproducing kernel.ProofBy Definition 4, we know that the kernel matrixKassociated with kernelKis symmetric,and it is easy to verify that

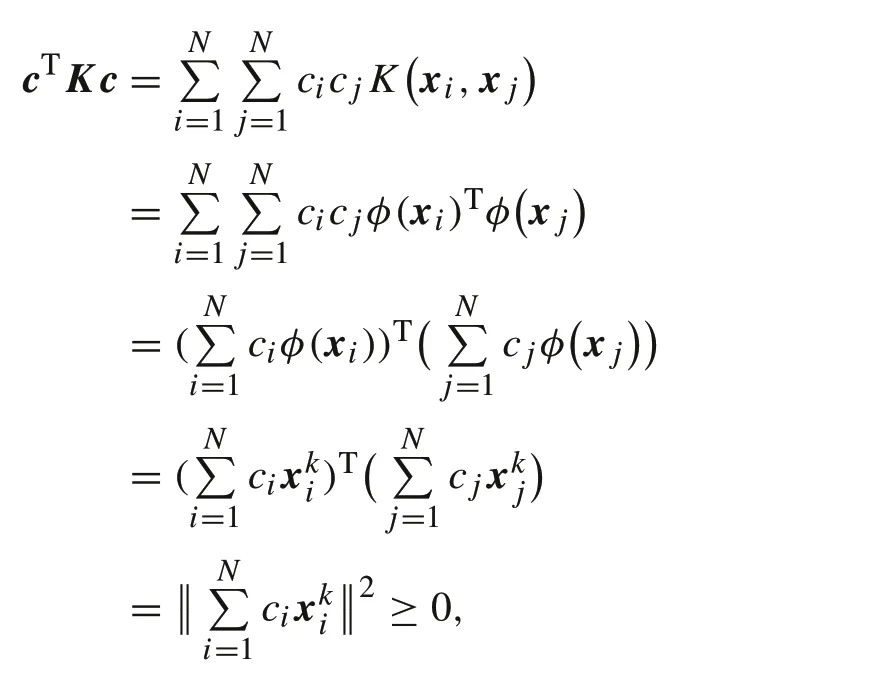
soKis positively definite. It follows that STP-kernelK(x,y)=〈φ(x),φ(y)〉Rnkis a positive definite kernel.By Remark 2,we know thatKis a Mercer kernel,also a reproducing kernel. ■

Next,we show that STP-kernel is a polynomial kernel.To begin with,we first introduce a lemma to support our result.

Lemma 2[21]For any positive integer m and any nonnegative integer n,the multinomial formula describes how a sum with m terms expands when raised to an arbitrary power n:

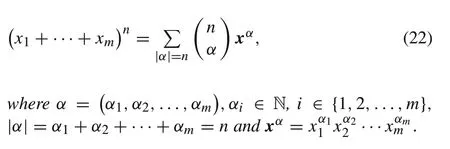
Proposition 5A STP-kernel generates a polynomial kernel,i.e.,

ProofWe only need to show

By Lemma 2 and (22), the right hand side of (24) can be written as

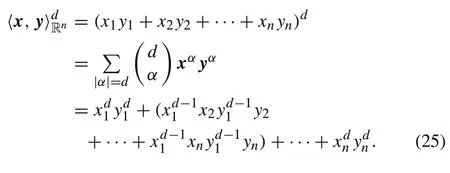
Let

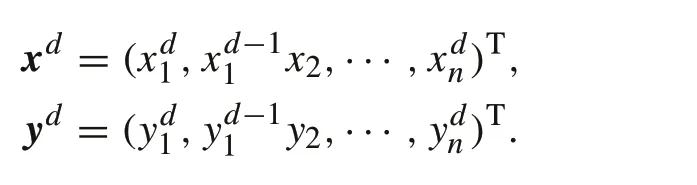
By rearranging every item in(25),we have

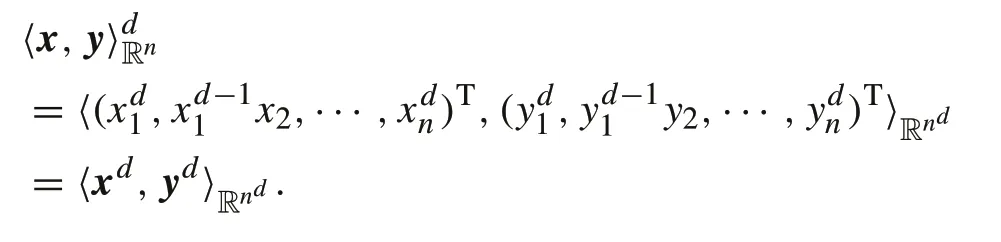
According to the definition of homogeneous polynomial kernel(11),the conclusion is drawn. ■

SoK(x,y)=〈x2,y2〉R4is a positive definite kernel.

It is natural we can generalize Proposition 5 to the nonhomogeneous kernel case.

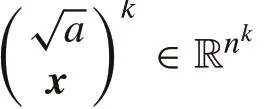
ProofThe proof isthe same as Proposition 5 ifwedefinex′=(√,xT)T∈RnandK′(x′,y′)=K(x,y).Leta=0,the homogeneous STP-kernel is obtained. ■

then

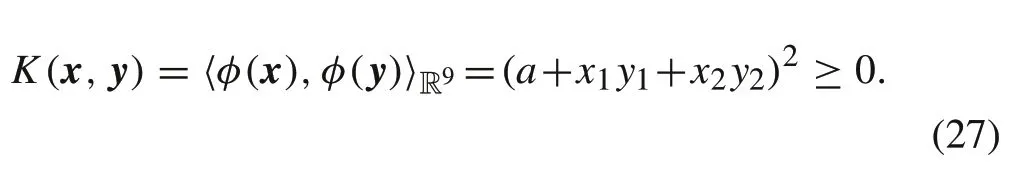
SoK(x,y)=〈φ(x),φ(y)〉R9is a positive definite kernel.

5 Reproducing Kernel Hilbert space of STP-kernel

In previous sections, we have shown STP-kernel is a reproducing kernel which determines a unique RKHS. In this section, we will investigate the structure properties of RKHS associated with homogeneous STP-kernel (nonhomogeneous STP-kernel can be done similarly).

We have already constructed STP-kernelK(x,y) =〈φ(x),φ(y)〉Rnkusing the feature mappingφ:x→xk,which maps everyndimensional data pointx∈Rnintonkdimensional feature space Rnk. Next, we show how we specify the RKHS of the STP-kernel. Let us describe it as follows.

For clarity, we will introduce some notations (Refer to the proof of Theorem 1 in[19]for details).Here we briefly introduce three Hilbert spacesHd,HKandH■:

HK:RKHS of homogeneous polynomial kernel;

Hd:Hilbert space of homogeneous polynomials;

H■:the RKHS of STP-kernel,

relations among which are explored more detailed in the sequel.

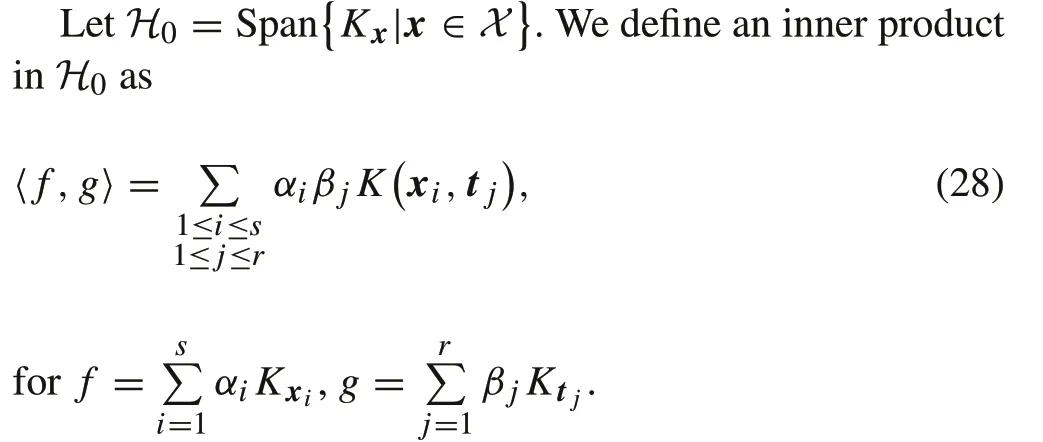
LetHKbe the completion ofH0with the associated norm.If the kernel ofHKis a homogeneous polynomial kernel with feature mapping

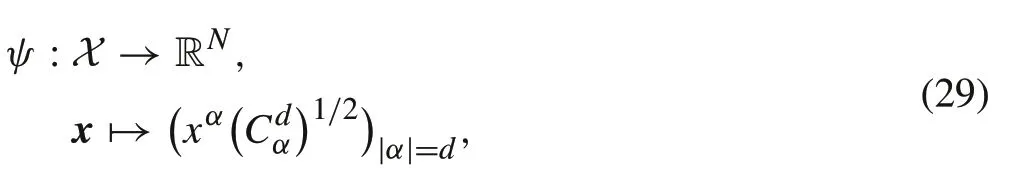
then,forx,t∈X,we have

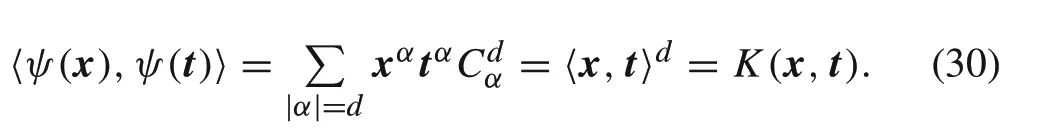
From Theorem 1,it concludes thatK(·,·)is a Mercer kernel,also a reproducing kernel.We can makeHdan inner product space by taking

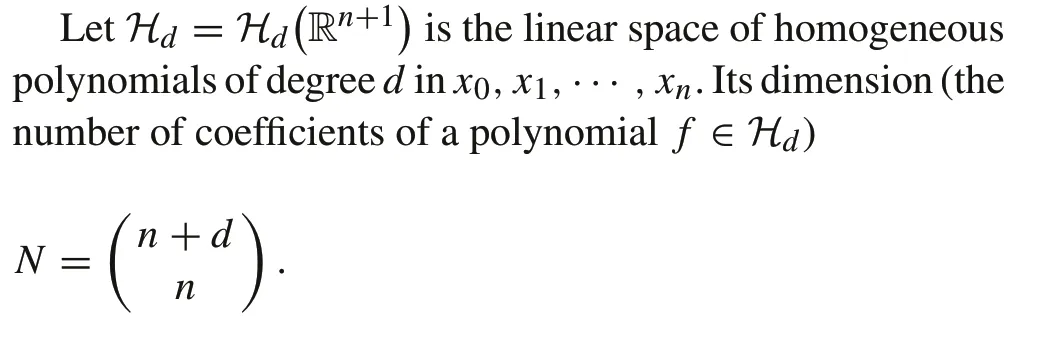
forf,g∈Hd,f= Σwαxα,g= Σvαxα. This inner product,called the Weyl inner product,satisfies

|f(x)|≤‖f‖w‖x‖d,

where‖f‖wdenotes the norm induced by〈·〉W,and‖x‖is Euclid norm ofx∈Rn+1.

Then,we have the following result aboutHKandHd.

Proposition 7[19]Both HK and Hd are isomorphic as function spaces and inner product spaces,denoted by HK∼=Hd.

Considering STP-kernel together with the above two kernels,we have the following theorem.

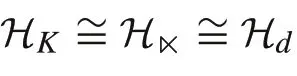
ProofWe only need to address two issues as follows:

1. They have the same generator setH0.

2. They have the same inner product though their expressions are different.

By Proposition 7,we have thatHKHdas RHKS,the remaining task for us is to verifyH■has the same generator setH0and inner product asHKandHd.The former can be seen by(23),the later can be seen obviously by Proposition 5. Relations amongH■,HKandHdcan be seen from the commutative diagram(Fig.3).

By the commutative diagram (Fig. 3), we have the following equations. Three pairs of equations in sides of the tetrahedron:

Three pairs of equations in underside of the tetrahedron:

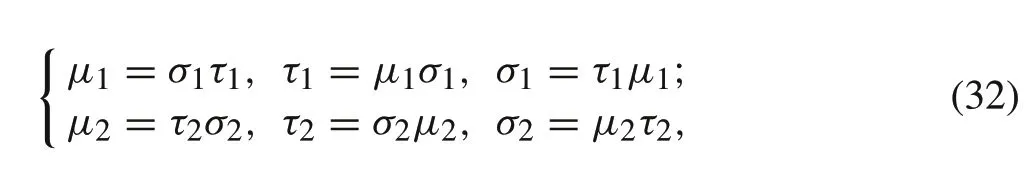
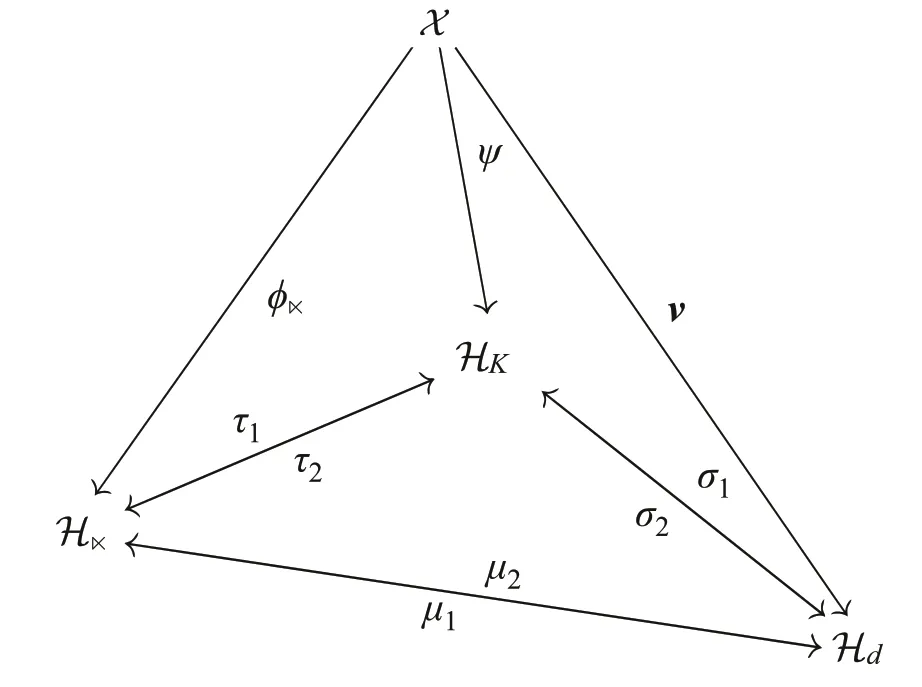
Fig.3 Commutative diagram

whereτ1→σ1→μ1→τ1is clockwise, whileτ2→μ2→σ2→τ2is anticlockwise.

Letx=(x1,x2,···,xn)T∈X⊆Rnand

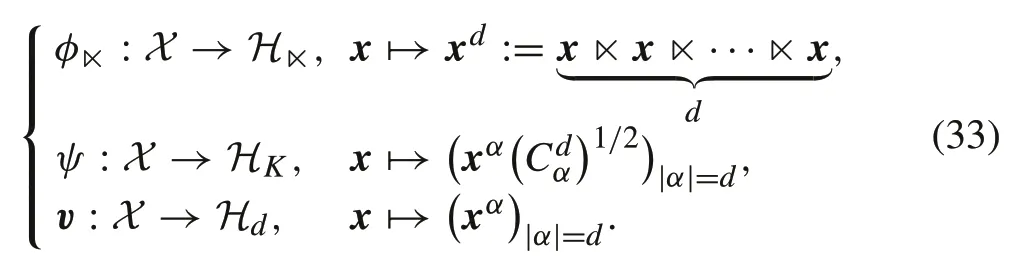
Then,linear mappingsσ1,σ2;τ1,τ2;μ1,μ2are defined as follows:

The proof of Theorem 3 shows us an algorithm for finding RKHSH,so the following result is trivial.

Proposition 8His the RKHS associated with STP-kernel,and it is a proper subspace ofRnk.

ProofIt can be induced directly from Theorem 3. ■

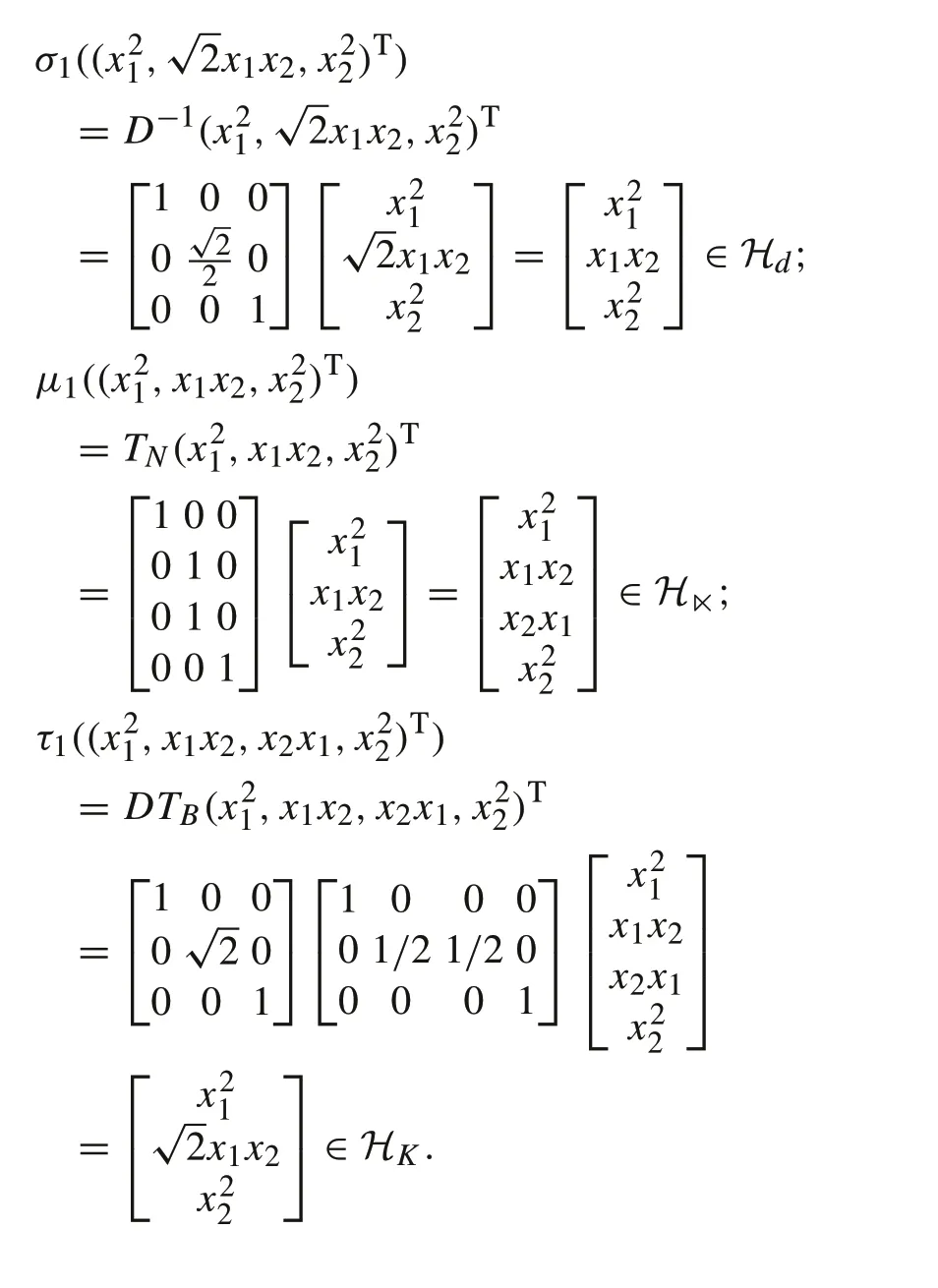
Next,we take an example to make clear the equivalence ofH,HKandHd.

Example 6Forn=d= 2,x=(x1,x2)T,then the feature mappings ofH,HKandHdare written as follows:

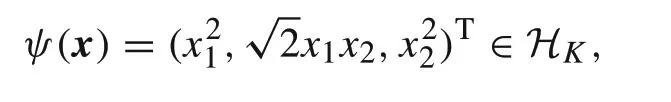
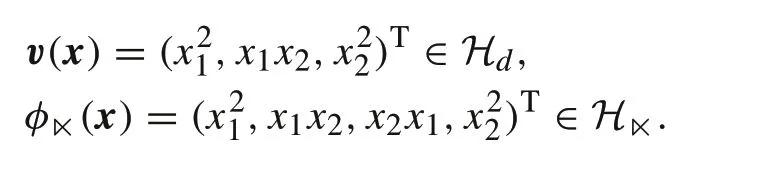
Then, by (32)–(34), transformations amongHK,Hd,H■are written as follows:

6 Conclusion

In this paper,the STP-kernel is first put forward for the SVMbased nonlinear classification.The proposed STP-kernel can produce the well-known polynomial kernel.Certain theoretical properties are studied,including the solution existence,reproducing properties of the STP-kernel. Particularly, we investigate relations between the STP-kernel and the polynomial kernel in theory.Numerical examples are conducted to investigate the effectiveness and efficiency of the proposed STP-kernel model.

AcknowledgementsWe thank Prof. Daizhan Cheng for giving some valuablesuggestions,andalsotheanonymousreviewersfortheirhelpful comments.