Non-iterative Cauchy kernel-based maximum correntropy cubature Kalman filter for non-Gaussian systems
2022-02-11AasthaDakRahulRadhakrishnan
Aastha Dak·Rahul Radhakrishnan
Received:20 May 2022/Revised:15 August 2022/Accepted:22 August 2022/Published online:17 October 2022
©The Author(s),under exclusive licence to South China University of Technology and Academy of Mathematics and Systems Science,Chinese Academy of Sciences 2022
Abstract This article addresses the nonlinear state estimation problem where the conventional Gaussian assumption is completely relaxed.Here,the uncertainties in process and measurements are assumed non-Gaussian,such that the maximum correntropy criterion(MCC)is chosen to replace the conventional minimum mean square error criterion.Furthermore,the MCC is realized using Gaussian as well as Cauchy kernels by defining an appropriate cost function.Simulation results demonstrate the superior estimation accuracy of the developed estimators for two nonlinear estimation problems.
Keywords Maximum correntropy criterion·Cubature Kalman filter·Non-Gaussian noise·Cauchy kernel·Gaussian kernel
1 Introduction
Nonlinear state estimation has great significance in signal processing,target tracking,information fusion,cooperative navigation,etc.,as most of the real-life problems are inherently nonlinear in nature[1–3].This nonlinear nature restricts the practitioners from obtaining an optimal solution, even after assuming that the uncertainties follow a Gaussian density.Hence,only sub-optimal solutions are available.Among suchsub-optimalsolutions,theextendedKalmanfilter(EKF)was the main estimator that practitioners relied on for many decades. However, the disadvantages of EKF such as poor estimation accuracy in the presence of high initial uncertainty and nonlinearity of models urged the practitioners to develop a new family of estimators.They were the unscented Kalman filter(UKF),cubature Kalman filter(CKF),cubature quadrature Kalman filter(CQKF),new sigma point Kalman filter (NSKF), etc. [4–7]. All these algorithms differ in the way they approximate the Gaussian prior and posterior with a set of deterministic points and weights.In many applications such as target tracking, power systems, etc., the Gaussian assumption for uncertainties is violated by significant outliers [8–10]. Under such conditions, the above-mentioned estimators result in poor estimation accuracy and may even fail to provide an estimate.
To handle non-Gaussian uncertainties, estimation algorithms, such as the particle filter (PF) [11] and Gaussian sum filter[12],are often preferred.However,they are associated with high computational load,especially in the case of PF.Moreover,in the presence of large non-Gaussian uncertainties,the estimation performance of Gaussian sum filters tends to degrade. Hence, an estimation algorithm that can effectively handle non-Gaussian uncertainties with moderate computational cost is the need of the hour. Recently, considerable attention has been paid to estimation algorithms developed based on the correntropy criterion starting from the correntropy Kalman filter for linear systems [13,14].However,it had the disadvantage of not considering the propagation of error covariance matrix [15,16]. To overcome this limitation, a maximum correntropy Kalman filter was derived, which used a fixed-point iterative method to limit the effect of non-Gaussian noise with a slight increase in computational cost[17,18].
Extension of this formulation based on maximum correntropy criterion (MCC) for nonlinear systems was reported in[19,20].However,the limitation of these algorithms was that they involve certain matrix inversion that could become singular in the presence of large non-Gaussian uncertainties[21,22].This numerical instability in the algorithm was overcome by the maximum correntropy unscented Kalman filter (MCUKF) formulation by reporting a series of algorithms like MCUKF-constant, MCUKF-adaptive, and the information filter [9]. However, the above-mentioned algorithms considered non-Gaussian uncertainties only in the noise associated with the measurements. While coming to non-Gaussian uncertainties in both process and measurement models,very few algorithms are available even for the linear systems[23,24].For nonlinear systems,algorithms available are iterative in nature resulting in increased computational cost[25].According to the best of the authors’knowledge,non-iterative state estimation algorithms for both nonlinear and non-Gaussian systems are not addressed in the literature.
In this work,a non-iterative estimation algorithm is proposed that can address the problem of nonlinear estimation where both the process and measurement uncertainties are assumed non-Gaussian.This is achieved by embedding the MCC based on Gaussian as well as Cauchy kernel functions in the traditional CKF.Recently,the Cauchy kernel has been reported in the literature as an alternative to the Gaussian kernel for achieving better estimation accuracy in the presenceoflargemulti-dimensionalnon-Gaussiannoise[26–28].Moreover,the Cauchy kernel is reported to give stable estimation performance for a larger range of kernel bandwidth in comparison to the Gaussian kernel[26].The developed estimation algorithms based on Gaussian and Cauchy kernels are termed as MCG−CKF and MCC−CKF,respectively.
2 Cubature Kalman filter(CKF)
Let us consider a nonlinear process and measurement model described in the discrete-time domain as
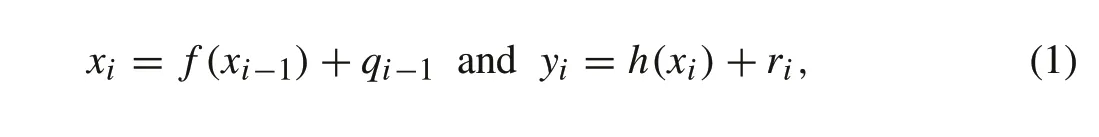
wherex∈Rnrepresents anndimensional state vector andy∈Rmrepresents themdimensional measurement vector.Here,f(·)andh(·)are known nonlinear functions representing process and measurement dynamics,respectively.
In the nonlinear Bayesian framework, integrals encountered are intractable in nature.Hence,a numerical approximationmethodhastobeadoptedforgeneratingasub-optimal solution.In CKF,this is achieved using the spherical radial cubature rule where the integral is decoupled into spherical and radial components[5].Then,these components are numerically approximated using the spherical cubature and Gauss quadrature rules,respectively.Let the intractable integral be expressed as
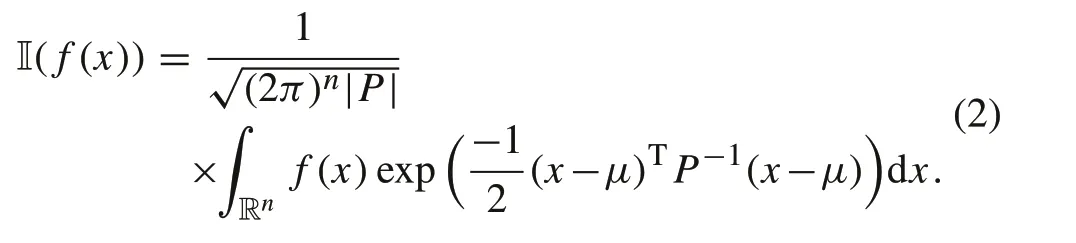
To express this integral in the spherical coordinate system,the transformationx=Sr Z+μis considered,whereSis the Cholesky decomposition ofPwith‖Z‖ = 1.Then,Eq.(2)becomes

Here,[u]iis the set of cubature points lying at the intersection points oftheunithyper-sphe√reandthecoordinateaxes.After achangeinvariablel=r/Eq.(3)becomes
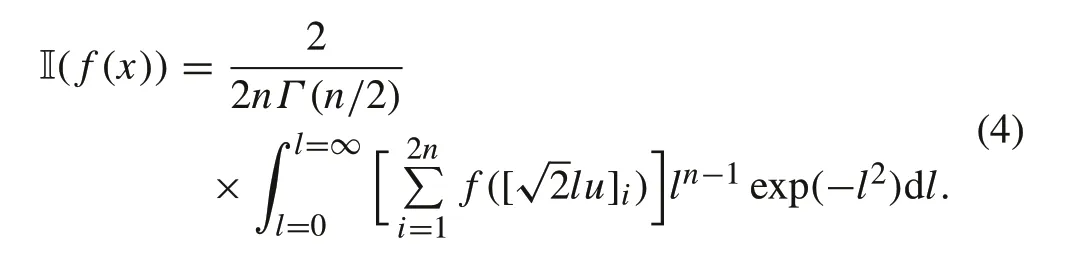

It is to be noted in Eq.(2)that the integral is assumed to be of the formf(x)×Gaussian density.Even though,in nonlinear state estimation,the densities encountered are non-Gaussian, they are still approximated as Gaussian. Hence,the spherical radial rule for the numerical approximation of integrals and the corresponding filtering framework provides an estimate with reasonable accuracy.However,this estimation accuracy can deteriorate in the presence of non-Gaussian uncertainties in the process as well as in the measurements[9,17]. This calls for a more robust CKF-based estimation framework that can effectively handle non-Gaussian uncertainties.To achieve this,the maximum correntropy criterion is used to reformulate the conventional CKF estimation framework.
3 Maximum correntropy criterion
Correntropy is a similarity measure of two random variablesXandY,defined as
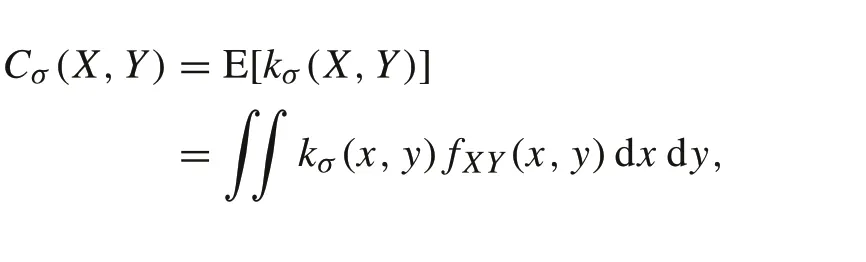
wherekσ(·)usually denotes a Gaussian kernel function and E[·]is the expectation operator.If only a finite number of data pointsNare available,then the sample estimator is given as
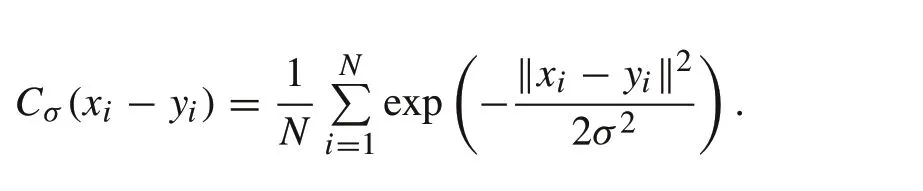
It is positive and bounded,and reaches its maximum if and only ifX=Y, thus leading to the maximum correntropy criterion (MCC). Correntropy can also be expressed as the weighted sum of all even order moments of(xi−yi)by taking the Taylor series expansion of the Gaussian kernel function given as
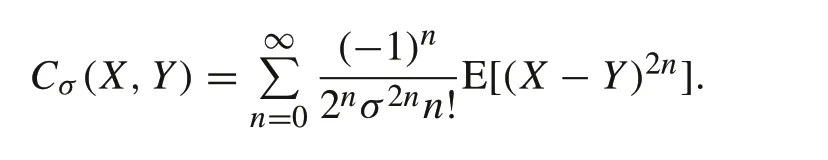
As an alternative to the Gaussian kernel,the Cauchy kernel could be used to define MCC for the development of estimators.The Cauchy kernel is defined as
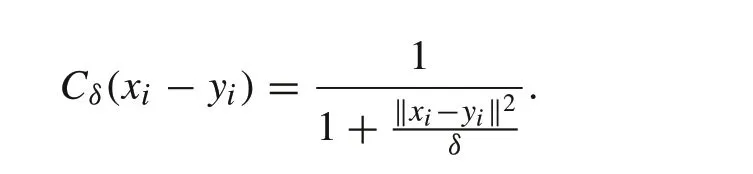
Here,δis a positive scalar representing the Cauchy kernel bandwidth.Similar to the Gaussian kernel,it can be shown that the Cauchy kernel also incorporates the higher order moments[29]given as
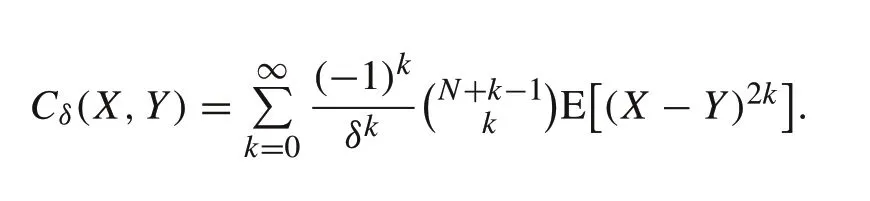
4 Derivation of Gaussian kernel-based maximum correntropy CKF(MCG–CKF)
To derive the MCC-based estimation algorithm for non-Gaussian systems,we consider a cost function

To guarantee the convergence of algorithm to a corresponding conventional state estimator(when the kernel bandwidthσbecomes infinity), the values for weights in Eq.(5) are taken asα=2σ2andβ=−2σ2.Then,Eq.(6)becomes
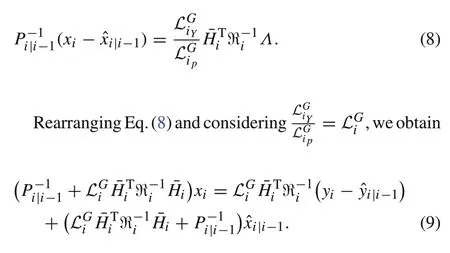
Sinceis related toxi,Eq.(9)represents a fixed-point equation that can be solved using the fixed-point iteration algorithm consideringxiequal to ˆxi|i−1in.However,as mentioned in[17,20]and[9],a single iteration is sufficient for achieving satisfactory estimation performance.Adopting the same approach leads to the modification of Eq.(9)as
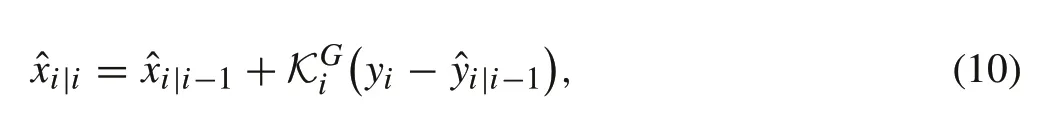
where

5 Derivation of Cauchy kernel-based maximum correntropy CKF(MCC–CKF)
To improve the performance in presence of large multidimensional noise,a nonlinear state estimator based on MCC and statistical linearization is developed based on the Cauchy kernel function.The corresponding cost function is defined as


Here also,is related toxi, and hence, Eq.(13) is a fixed-point equation that is to be solved using fixed-point iteration algorithm by assumingxiequal to ˆxi|i−1.Using the same justification that was adopted in the Gaussian kernel case that only a single iteration is required, the expression for posterior mean is obtained as

Theorem 1As the kernel bandwidth δ tends to infinity,the Cauchy kernel-based MC estimator reduces to the standard nonlinear state estimation algorithm.
ProofAs the time update is the same for the developed algorithms with respect to the standard nonlinear state estimators,the prior mean and covariance are unchanged. Hence, the focus shall be on the posterior mean and covariance. This implies that the Kalman gain equation has to be revisited.Whenδ→∞
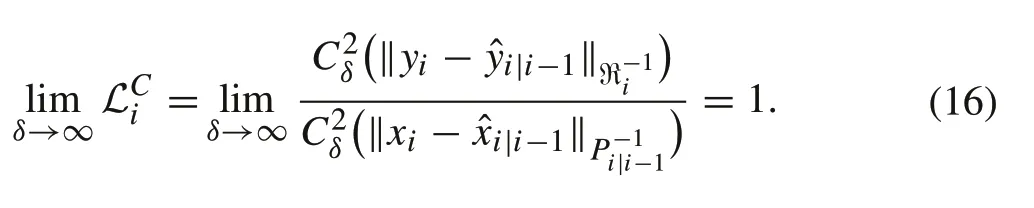
Substituting Ri,Eq.(16)andin,we have
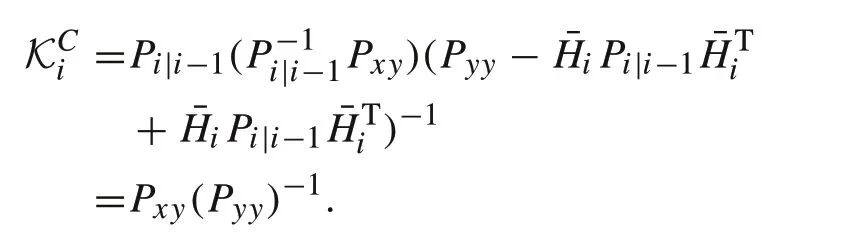
Since the expression ofis similar to the Kalman gain of standard nonlinear state estimator,posterior mean is also the same.From Eq.(15),the posterior covariancePi|ibecomes

Remark 1When the probability of occurrence of abnormal noise is very high,a smaller value ofδprovides better estimation accuracy.When the probability is less,a larger value ofδis preferred.
Remark 2The range ofδfor which robust and accurate estimation performance can be achieved is higher when compared to that ofσ. This means that more flexibility is associated with the choice ofδ,without hampering the estimation accuracy.
Remark 3The proposed algorithm can fail only if the scalar termsandendtoinfinity.Thiscanoccurintwoconditions:a)when sensor measurements are devoid of noise,and b)the assumed model is far off from the actual system.However, the sensor measurements are always noise corrupted,and for accurate state estimation,the assumed process model should resemble the dynamics of the actual system.
6 Algorithm for MCC–CKF
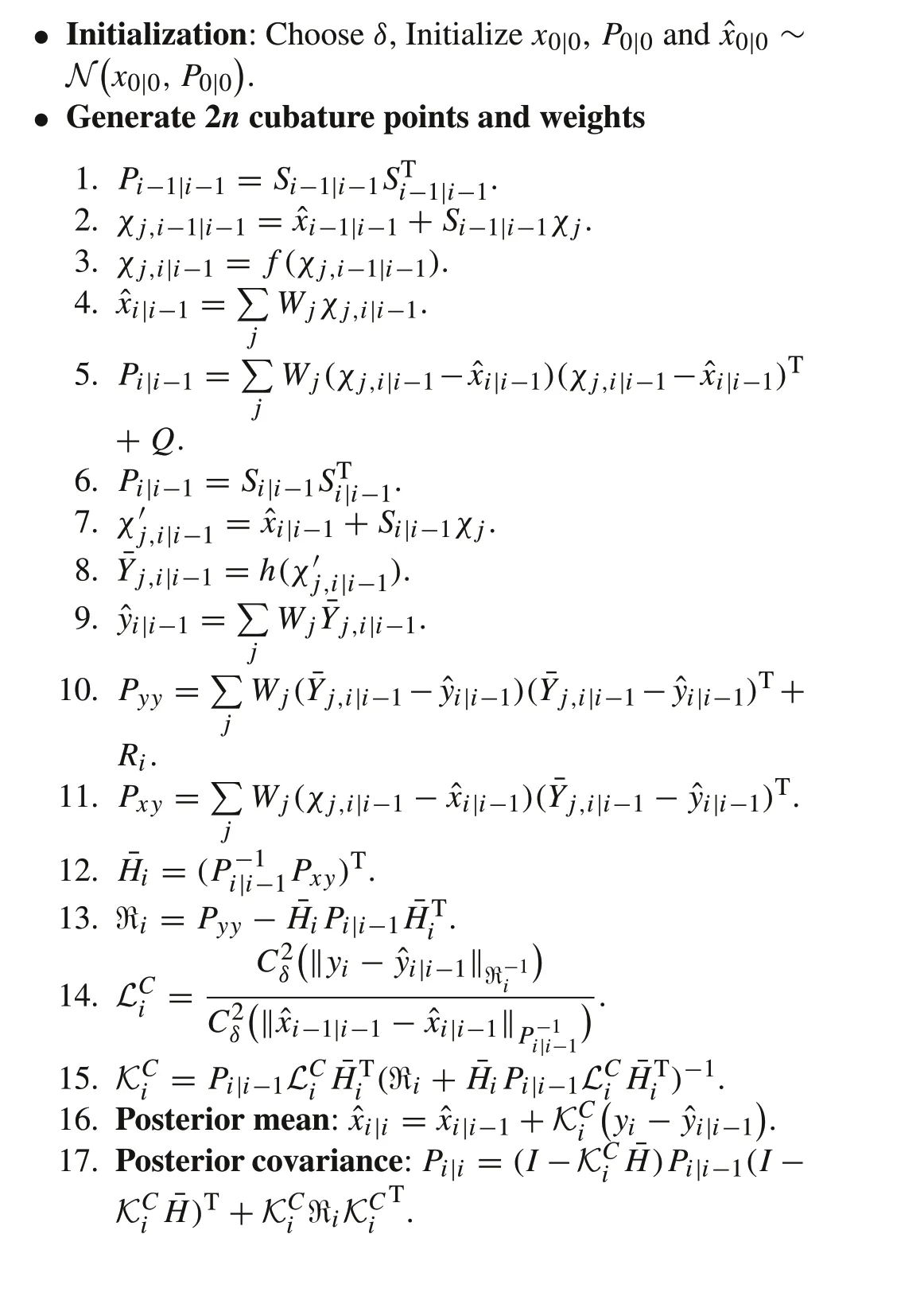
7 Computational complexity
Since the real-time implementation of the estimation algorithm is of utmost importance,the computational complexity of the proposed MCC−CKF is analyzed.The unit of computational complexity is usually measured in terms of floating point operations or flops.An addition,subtraction,multiplication, or division of two floating point numbers defines a flop.In Table 1,the computational complexity of each equation is given according to its numbering in Sect.6.Hence,it can be concluded that the total computational complexity of MCC−CKF is 14n3+16n2m+8n2+6nm+10nm2+3m2+5m+4n+4O(n3)+3O(m3)+2nO(f(·))+2nO(h(·)).Similarly,the computational complexity of MCG−CKF is analyzed and found to be two flop counts more than that of MCC−CKF.This is due to the extra flop counts required for the computation ofLGi.Furthermore,it can also be inferred that this is comparable with the computational complexity of the conventional CKF, which is 10n3+9n2+10nm+4n2m+6nm2+m2+m+2O(n3)+2nO(f(·))+2nO(h(·)).Now,with respect to the iterative MCC algorithms,the proposed algorithms have less computational complexity.This is because,for iterative algorithms,the computational complexity of corresponding equations will become a function of the number of iterations[17].However,for more clarity,the relative run-time of the algorithms is given in Table 6.

Table 1 Computational complexity of MCC −CKF
8 Simulations and results
To demonstrate the estimation accuracy of proposed algorithms MCG−CKF and MCC−CKF in comparison to the existing CKF, two nonlinear estimation problems are considered. The first problem is a 2D target tracking problem,whereas the second one is the popular Lorenz system.
8.1 Modeling of non-Gaussian noise
In this work,non-Gaussian uncertainties are modeled as glint noise. Glint noise is often mentioned in the radar target tracking literature where the measurement noise often shows non-Gaussian behavior because of the random wandering of the measured target position[10].It has a heavy-tailed non-Gaussian density with frequent outliers and has statistical
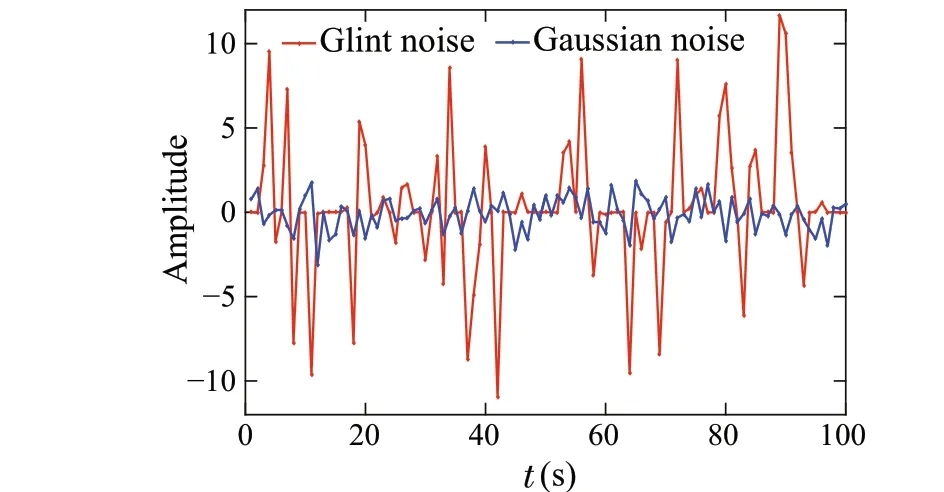
Fig.1 Glint noise
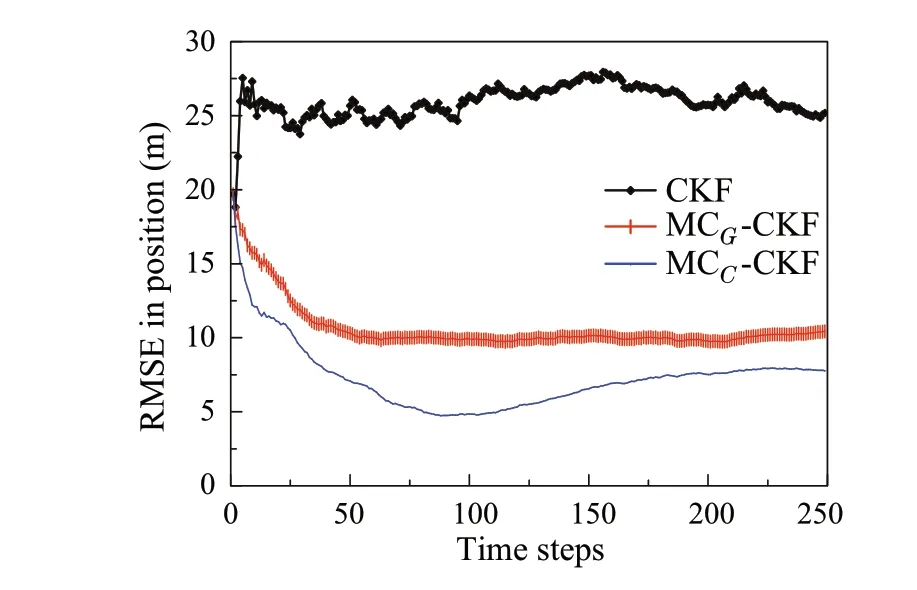
Fig.2 RMSE in position
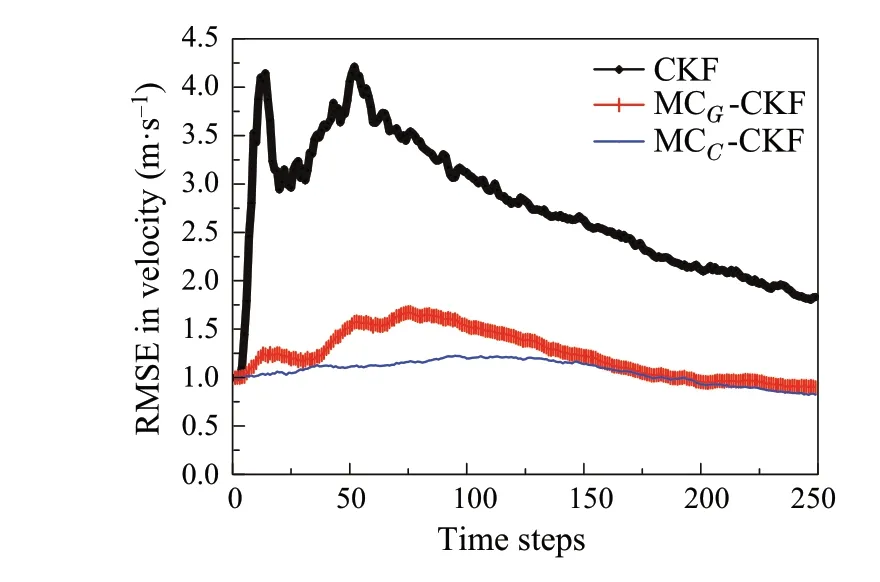
Fig.3 RMSE in velocity
characteristics that are significantly different from that of the white Gaussian noise.
An illustration for the same is given in Fig.1,where the plot indicates long-tailed behavior.The data in the tail region are known as outliers or glint spikes. Here, glint noise is modeledusingaweightedmixtureofGaussiandensities[30].It is represented asf(x)=(1 −∊)fg1(x)+∊fg2(x),where∊is the glint probability andfg1(x) ∼N(0,γ21),fg2(x) ∼N(0,γ22)withγ1/=γ2.
8.2 2D target tracking
A two-dimensional constant velocity target tracking problem is considered where the states to be estimated are the positionand velocity of the target.The measurements are range and azimuth angle obtained from a radar. The process model is represented as
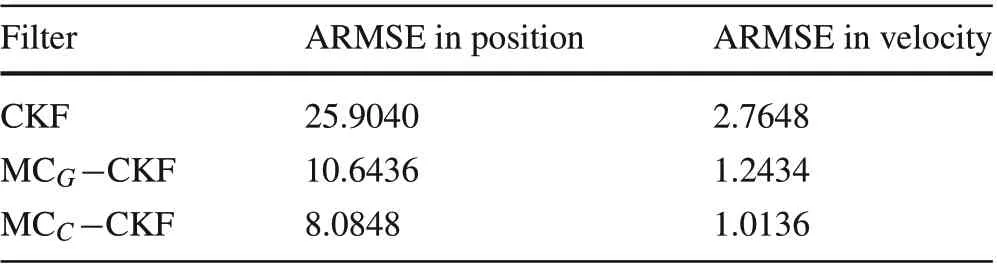
Table 2 ARMSE values in position and velocity
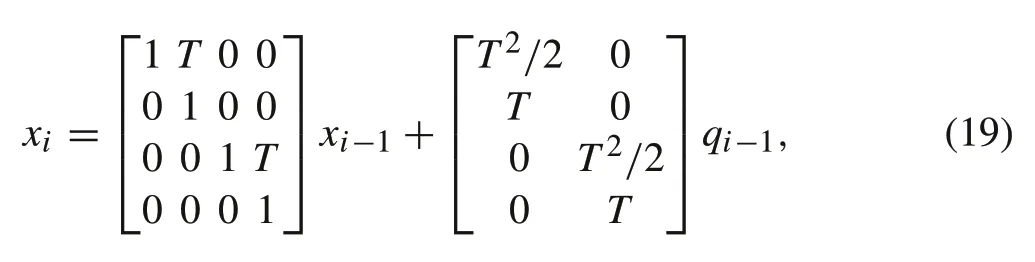
wherexi= [ξi˙ξi ηi˙ηi]Tis the system state.(ξi,ηi)denotes the position and(˙ξi, ˙ηi) denotes the velocity of target inxandydirections, respectively. Here,qiis the glint noise modeled as 0.6Nμ,diag{0.04,0.04}+0.4Nμ,diag{4,4}withμ= [0 0]Tand the sampling periodTis taken as 0.1s.The nonlinear measurement model is represented as
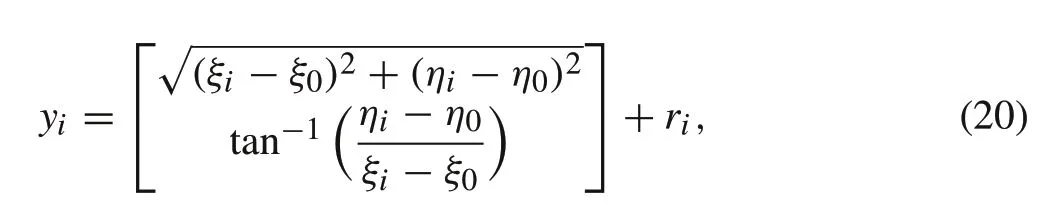
whereriis the measurement noise modeled as

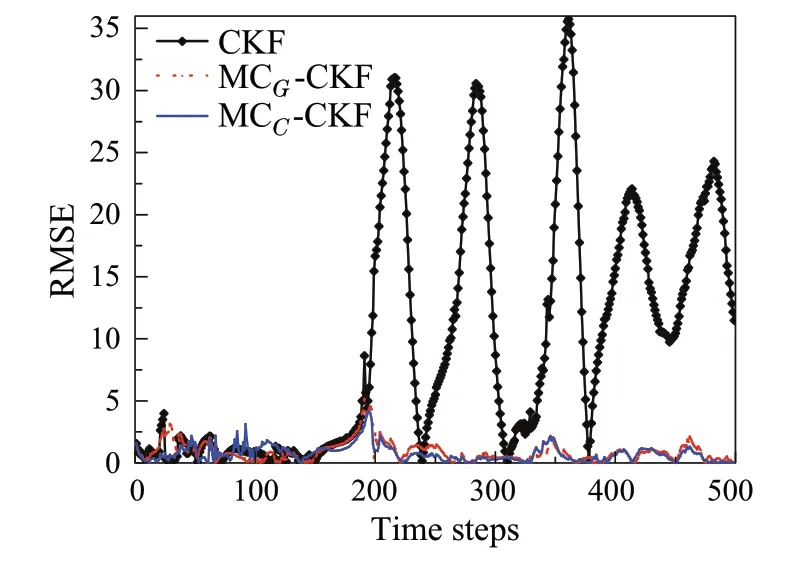
Fig.4 RMSE in x1
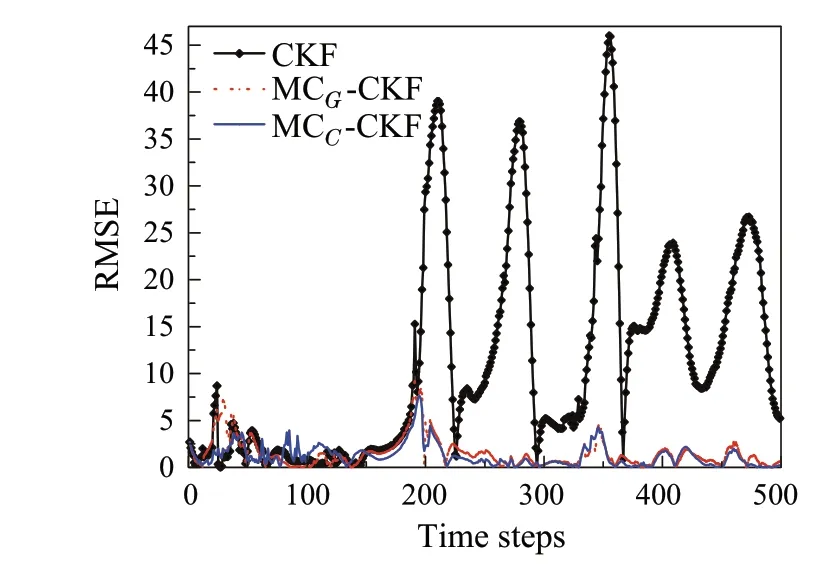
Fig.5 RMSE in x2
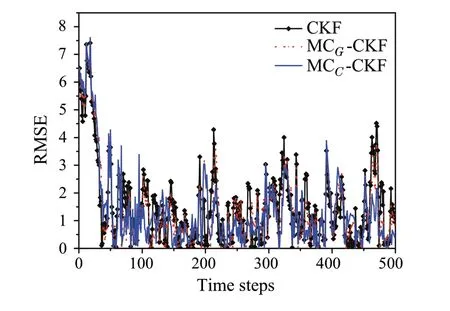
Fig.6 RMSE in x3
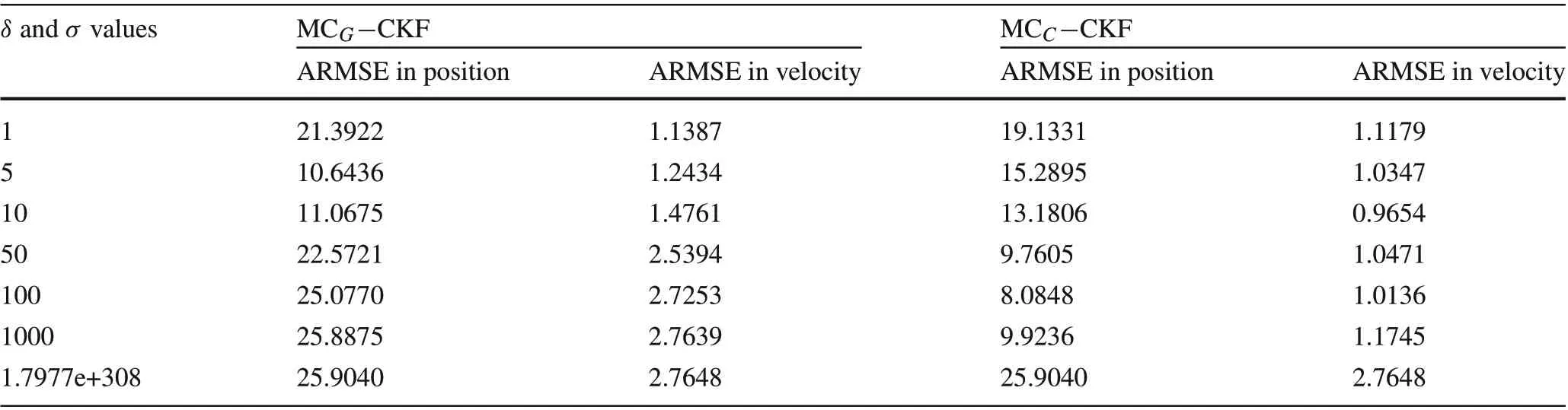
Table 3 Gaussian and Cauchy kernel bandwidth analysis on estimation accuracy
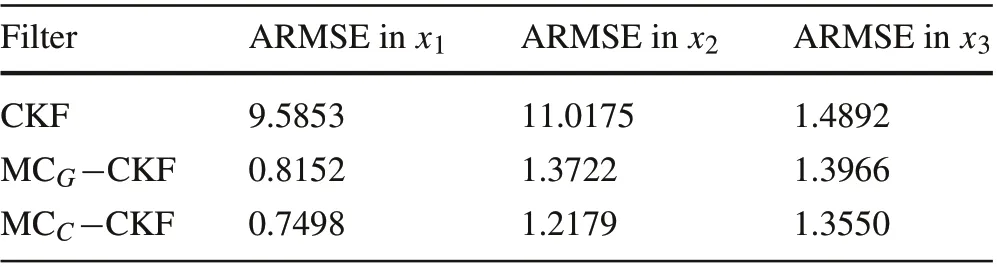
Table 4 ARMSE values in states x1,x2,and x3
To evaluate the performance of the developed estimators, root-mean-square error (RMSE) in resultant position and velocity is computed over 100 independent Monte Carlo runs where the simulation period lasted for 250 time steps.The RMSE in resultant position and velocity is evaluated and plotted in Figs. 2 and 3. From these figures, it can be inferred that the developed algorithms performed with superior estimation accuracy when subjected to glint noise in the process and measurements.At the same time,the estimation accuracy of the traditional CKF deteriorated significantly.Furthermore, it shall be noted that MCC−CKF performed with slightly higher estimation accuracy when compared to the MCG−CKF.From Fig.2,it shall be noted that the CKF incurred nearly five times more error than the developed MCC−CKF. This can be explained more precisely by calculating the average RMSE(ARMSE),that is the average of RMSE value over the time horizon. Table 2 shows the calculated ARMSE values and it can be observed that Cauchy kernel-based MC estimators incurred less estimation error than the Gaussian kernel-based MC estimator.All the simulations were carried out by taking Cauchy kernel bandwidth asδ= 100 and Gaussian kernel bandwidth asσ= 5,such that the best estimation accuracy can be achieved.
The effect on the estimation accuracy of developed filters according to their kernel bandwidth values is given in Table 3.Here,ARMSE is evaluated by varying the kernel bandwidth from unity to the largest possible value that the computing platform (MATLAB 2020a) can generate. As mentioned in Table 2,it can be observed that the least errors were incurred bythedevelopedalgorithms for kernel bandwidthvaluesσ=5 andδ= 100.Moreover,the convergence of the proposed algorithms to the conventional CKF is evident from Table 3.Whenσandδvalues assumed the largest possible value,i.e.,theoretically infinity,the ARMSE values of the proposed algorithms coincided with the ARMSE values of CKF.

Table 6 Relative run-time
8.3 Lorenz system
We consider the discrete-time Lorenz system which is one of the benchmark problems in nonlinear dynamics.The process and measurement equation is given by
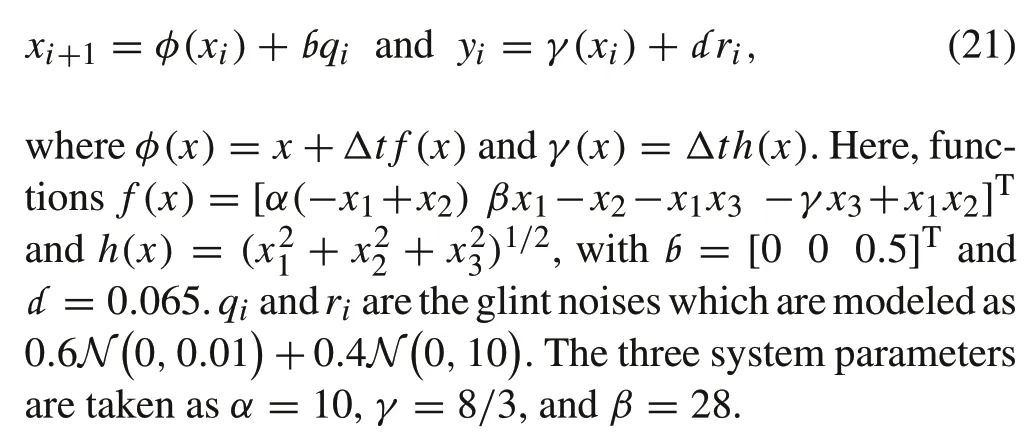
The initial truth value of state is taken asx0=[−0.2 −0.3 −0.5]Tand the sampling interval is taken asΔt= 0.01s. The initial posterior estimate is assumed as ˆx0|0= [1.35 −3 6]Twith initial error covarianceP0|0= 0.35I3.Figures4,5 and 6 show the RMSE in states for 100 Monte Carlo runs obtained by CKF, MCG−CKF and MCC−CKF.It can be observed that for the third state,no significant improvement has been achieved.However,for the other two states, the RMSE of the proposed filters is considerably less compared to the CKF.This illustrates the deterioration of estimation accuracy in the CKF when subjected to glint noise.
The same inference could be obtained from the ARMSE values given in Table 4,forσ=4 andδ=100.To demonstrate the effect of kernel bandwidth on accuracy, ARMSEfor variousσandδvalues is given in Table 5.From the table,it can be inferred that satisfactory estimation performance for MCG−CKF is obtained whenσ= 3,4 and 5. However, in the case of MCC−CKF, the range of values forδcan be varied from 70 to 200 without losing estimation accuracy. Moreover, when the bandwidth tends toward infinity,ARMSE values coincide with that of the conventional CKF.This again proves the convergence of proposed algorithms to the CKF,as mentioned in Theorem 1.
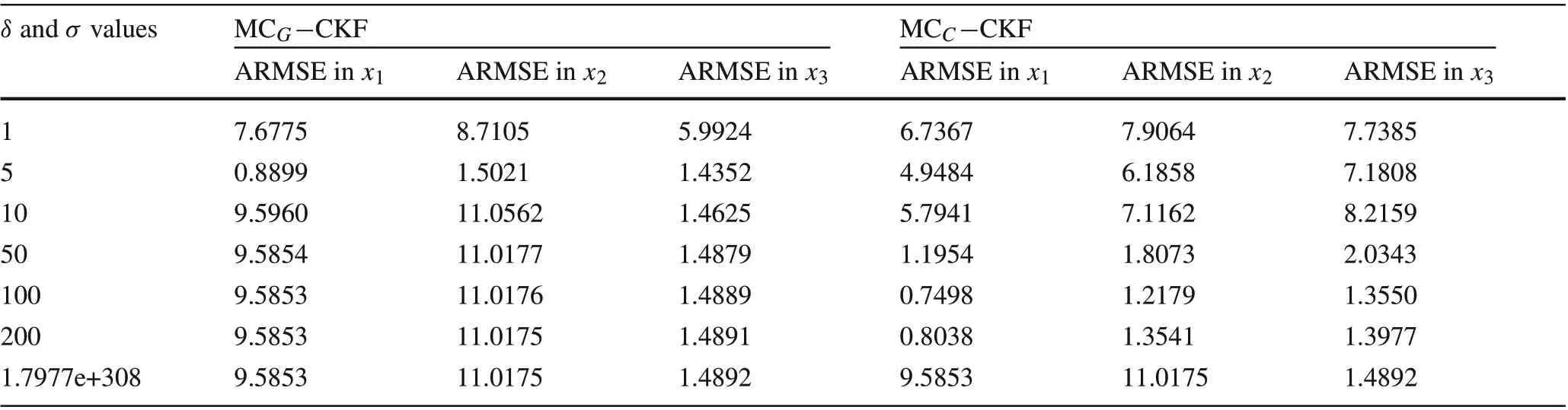
Table 5 Gaussian and Cauchy kernel bandwidth analysis on estimation accuracy
The relative run-time of the algorithms is computed and tabulated in Table 6.From this table,it can be observed that in comparison to the CKF,MCG−CKF and MCC−CKF have an increased run-time of 23%and 27%,respectively.Hence,it can be inferred that the proposed algorithms have almost similar run time.
9 Conclusion
In this work,new nonlinear estimation algorithms are developed to handle non-Gaussian noise in the process as well as in measurements,named MCG−CKF and MCC−CKF.It was developed by proposing the maximum correntropy criterion(MCC)as an alternative to minimum mean square error,by defining an appropriate cost function in terms of Gaussian and Cauchy kernel functions. From the simulation results,it can be inferred that the developed algorithms performed with improved estimation accuracy when compared to the conventional CKF, with MCC−CKF giving better estimation accuracy than MCG−CKF.Hence,it can be concluded that with proper choice of kernel bandwidth, the proposed algorithms can be a suitable alternative to the conventional CKF,when subjected to non-Gaussian uncertainties in both process and measurement models.
Funding This research was funded by SVNIT Surat Project No.2020-21/seed money/30.
杂志排行
Control Theory and Technology的其它文章
- State of health based battery reconfiguration for improved energy efficiency
- Design of semi-tensor product-based kernel function for SVM nonlinear classification
- Strong observability as a sufficient condition for non-singularity and lossless convexification in optimal control with mixed constraints
- Cooperative distributed state estimation:resilient topologies against smart spoofers
- Bipartite consensus for nonlinear time-delay multiagent systems via time-varying gain control method
- Discrete-time sliding mode control with power rate exponential reaching law of a pneumatic artificial muscle system
