对一道平面几何问题的探索

湖南省桃江县第一中学 (413400) 胡芳举

问题如图1，设P为ΔABC内一点，满足∠APB=90°+∠ACP，∠APC=90°+∠ABP，求证：P为ΔABC的内心.

图1

该题由湖南师大叶军教授提供，用几何法不难证明，接着叶老师又提出了如下两个探究问题：

变式1 设P为ΔABC内一点，满足∠APB=90°+∠ACP，∠APC=90°+∠PBC，则P为ΔABC的内心吗？

变式2 设P为ΔABC内一点，满足∠APB=90°+∠PCB，∠APC=90°+∠PBC，则P为ΔABC的内心吗？

本文将解答这两个变式，并提出几个新命题.

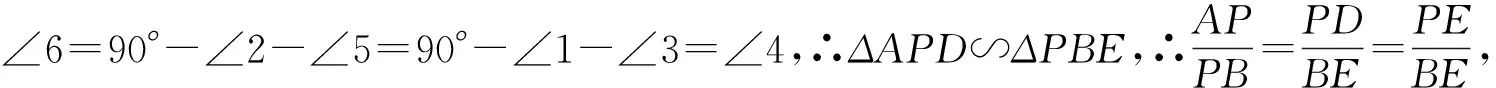
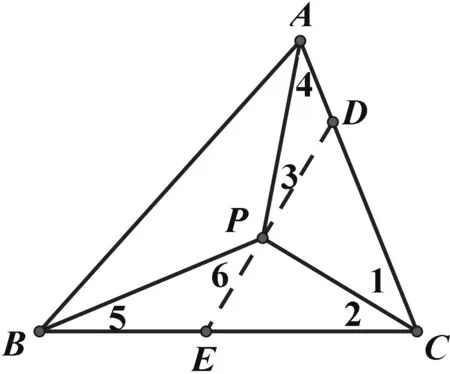
图2

变式2不成立，反例如下：任作钝角ΔBPC(使∠BPC为钝角，如图3)，再作∠CPQ=90°+∠PBC，则∠QPB=360°-∠CPQ-∠BPC=360°-(90°+∠PBC)-(180°-∠PBC-∠PCB)=90°+∠PCB，在射线PQ上任取一点A，则ΔABC满足题设条件，但显然点P不一定为ΔABC的内心.

图3

要变式2成立需要补充什么条件呢？经过进一步探索，得到了几个有趣的结论：

结论1 如图4，设P为ΔABC内一点，满足∠APB=90°+∠PCB，∠APC=90°+∠PBC，∠PAB=∠PAC，则P为ΔABC的内心或AB=AC.

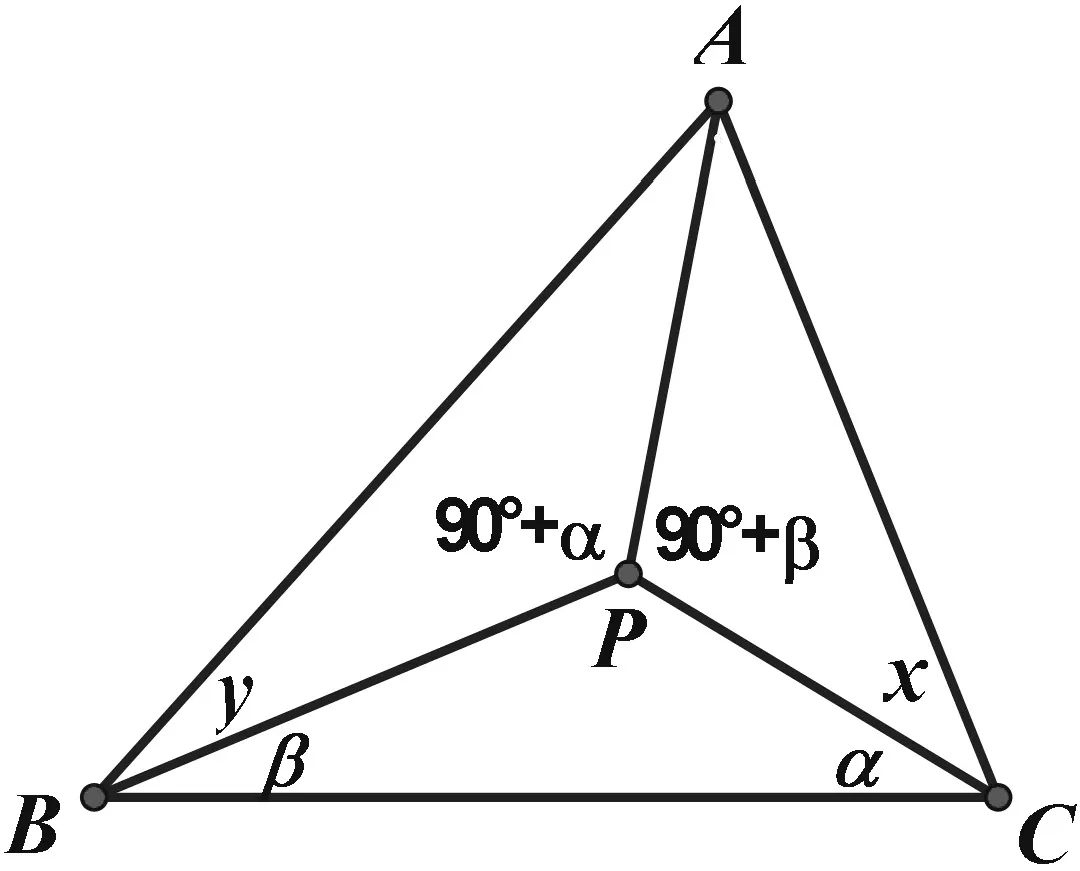
图4

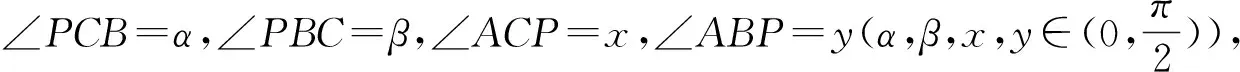
注：希望有读者能给出纯平面几何证明.

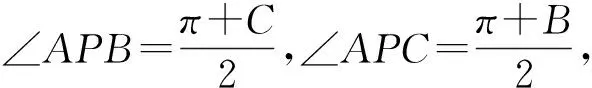
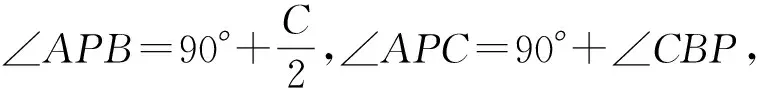
注：结论2，3，4可以仿结论1证明.