对一道课本习题的探究与拓展*

广东省中山市小榄中学 (528415) 吴银军

课本是我们教学的第一手资料，其中的多数习题具有较强的代表性，往往蕴含丰富的背景和深厚的内涵，值得广大师生深入的研究.笔者在讲授普通高中课程标准教科书(2019版)《选择性必修2》等差数列章节内容时，发现P25习题4.2第8题是关于两个等差数列的公共项问题，本文以该问题为例从解法和应用上作深入的探究，以期能抛砖引玉.

1 习题呈现与分析

有两个等差数列2,6,10，…，190及2,8,14，…，200，由这两个等差数列的公共项按从小到大的顺序组成一个新数列，求这个新数列的各项之和.

分析：该题考查的是等差数列问题，涉及到的知识点有两个等差数列的公共项构成新数列的特征，等差数列求和公式，考查了观察、分析、逻辑推理能力和等差数列前n项和公式的应用.这是一道平朴蕴奇，内涵丰富、极具拓展价值的优质试题.下面从这道试题的解法谈起，来探究和拓展两数列有公共项一类问题的解法，并从中得到一些启示.

2 探究解法 活跃思维

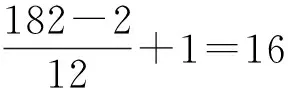
评注：考虑到该题中的两个数列均为等差数列，所以它们的公共项具有规律性,通过列举得到由两个数列的公共项构成的数列，进而求得新数列前n项和.在找公共项的时候，比较好的办法是在公差大的数列里面来找，因为间隔小，且项与项间隔相等，本解法适用于项数不多的、比较简单的两数列公共项问题.

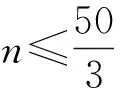
评注：依据两个等差数列的首项和公差的特征，不难看出两个数列的公共项所构成的新数列仍然是等差数列，且公差是两个等差数列公差的最小公倍数的规律求解.

由于该题是两个等差数列的公共项问题，从公共项的本质看，公共项也就是数列的相同项，不难求得两个数列的通项分别为4n-2,6n-4，也就是说关于m,n的不定方程4n-2=6m-4存在整数解，利用数的整除性解不定方程.

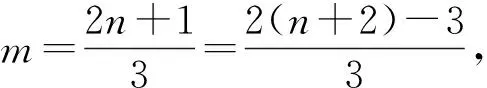
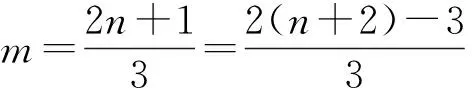
对于两个等差数列的公共项问题，还有没有更一般的方法呢？因为公共项就是两个数列中的相同项，我们从中选取一个数列，一般选取数列中的项增加“较快”的数列，假如该数列的第n项是两个数列的公共项，然后逐一递推验证该数列的第n+1项、第n+2项、……是否是两个数列的公共项，进一步从中找到规律，得到两个数列公共项从小到大排列的数列的通项公式.

评注：由解法4可知利用“递推找项法”求两个等差数列{an}、{bn}的公共项所构成的新数列{cn}的一般步骤为：(1)设ck=an=bm，从中得到项数m,n的关系；(2)在项数增加“较快”的数列({bm})中依次验证某个相同项(如bm)后面的递推项(bm+1,bm+2…)，并将其项的表达式与另一个数列{an}的通项比较，判断后面的递推项是否是另一个数列{an}的通项，从而发现新的公共项；(3)在发现的公共项ck,ck+1之间的递推关系得到新数列{cn}的通项公式.

3 提炼通法 总结升华

由以上解法不难看出，对于求两个等差数列{an}、{bn}的公共项所构成的新数列{cn}问题，“递推找项法”相对于解不定方程法更易于操作和理解，可以说，“递推找项法”是求两个等差数列{an}、{bn}的公共项所构成的新数列{cn}的一种“通性通法”. 其实“递推找项法”的应用远不止于此，它除了能解决两个等差数列的公共项问题以外，还可以解决两个等比数列的公共项问题，一个等差数列与一个等比数列的公共项问题，甚至于一个等比数列与多项式型数列的公共项问题.

4 拓展应用 拾级而上

(1)两个等差数列的公共项问题

例1 数列{an}与{bn}的通项分别为an=3n-1,bn=2n+1，它们的公共项由小到大排列得到的新数列{cn}，求数列{cn}的通项公式.

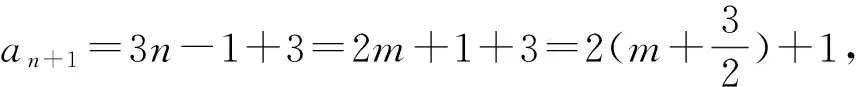
(2)两个等比数列的公共项问题

例2 数列{an}与{bn}的通项分别为an=3n,bn=9n，它们的公共项由小到大排列得到的新数列{cn}，求数列{cn}的通项公式.

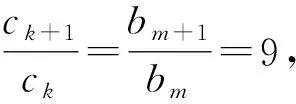
(3)等差数列与等比数列的公共项问题

例3 数列{an}与{bn}的通项分别为an=2n,bn=3n+1，它们的公共项由小到大排列得到的新数列{cn}，求数列{cn}的通项公式.

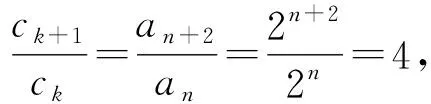
(4)等比数列与多项式的公共项问题

例4 数列{an}与{bn}的通项分别为an=22n-1,bn=n3，它们的公共项由小到大排列得到的新数列{cn}，求数列{cn}的通项公式.

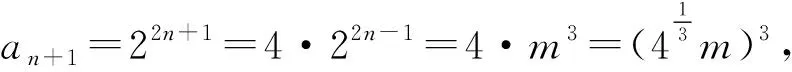
综合上述典例可知，“递推找项法”是一种在整体上从一个数列中寻找公共项的解题方法，这种方法通俗易懂，可操作性强，适用范围较广泛，是一种求两个数列公共项的“通性通法”.

5 解后反思 引领教学

课本既是学生学习的蓝本，又是教师教学的依据，课本中的例题、习题是教材编写者精心挑选或设计出来的，这些题目往往简明扼要、难度适当、编排合理，是一些难得的好题，它们在知识上具有典型性，在方法上具有示范性；所以我们要引导学生及时总结、反思和探究，寻求其内在的背景和数学思想，由会解一道题到会解一类题，形成有效的思维链，加强数学思维的拓展优化.另外，从不同的思维角度分析同一个问题，可以得到不同的解法，从数学知识本身的角度看，可以发现知识之间的相互联系，体会转化的过程，还可以构建知识网络体系，从而学生在学习过程中不仅掌握了基本的解题技能，还培养了思维的广阔性、深刻性、灵活性以及创新性，让学生对学习内容有一个整体认识，并将知识融会贯通，举一反三，开阔视野，活跃思维，才能实现解题探究价值的最大化.