利用“基本思路”解一道中考几何压轴题

湖南省常德市第三中学 (415000) 陆信明

中考几何压轴题综合性较强，一般需要构造辅助线求解，让学生心生畏惧，难以突破．究其原因，除了试题本身承载着选拔功能，有较高难度外，学生对一些重要的“基本思路”不重视、不熟练、理解不到位也是不容忽视的原因．在初中平面几何中，“基本思路”一般指依据教材中的一些基本定理、重要结论为待解决的问题所提供的解题方向，例如：要证明两直线平行，“基本思路”一般为证明同位角或内错角相等、同旁内角互补或证明平行四边形、中位线等．这些“基本思路”看似平淡无奇，实则作用巨大，下面本文结合2021年湖南省常德市中考数学几何压轴题对利用“基本思路”解题进行说明.

题目如图1，在△ABC中，AB=AC，N是BC边上的一点，D为AN的中点，过点A作BC的平行线交CD的延长线于T，且AT=BN，连接BT.

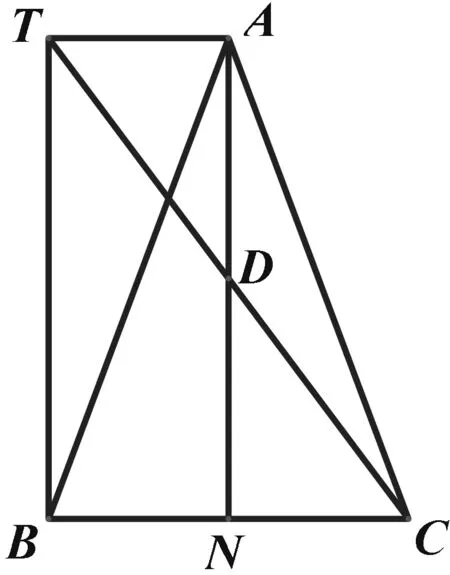
图1

(1)求证：BN=CN；

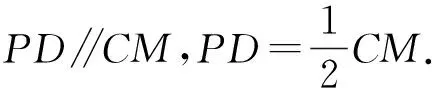
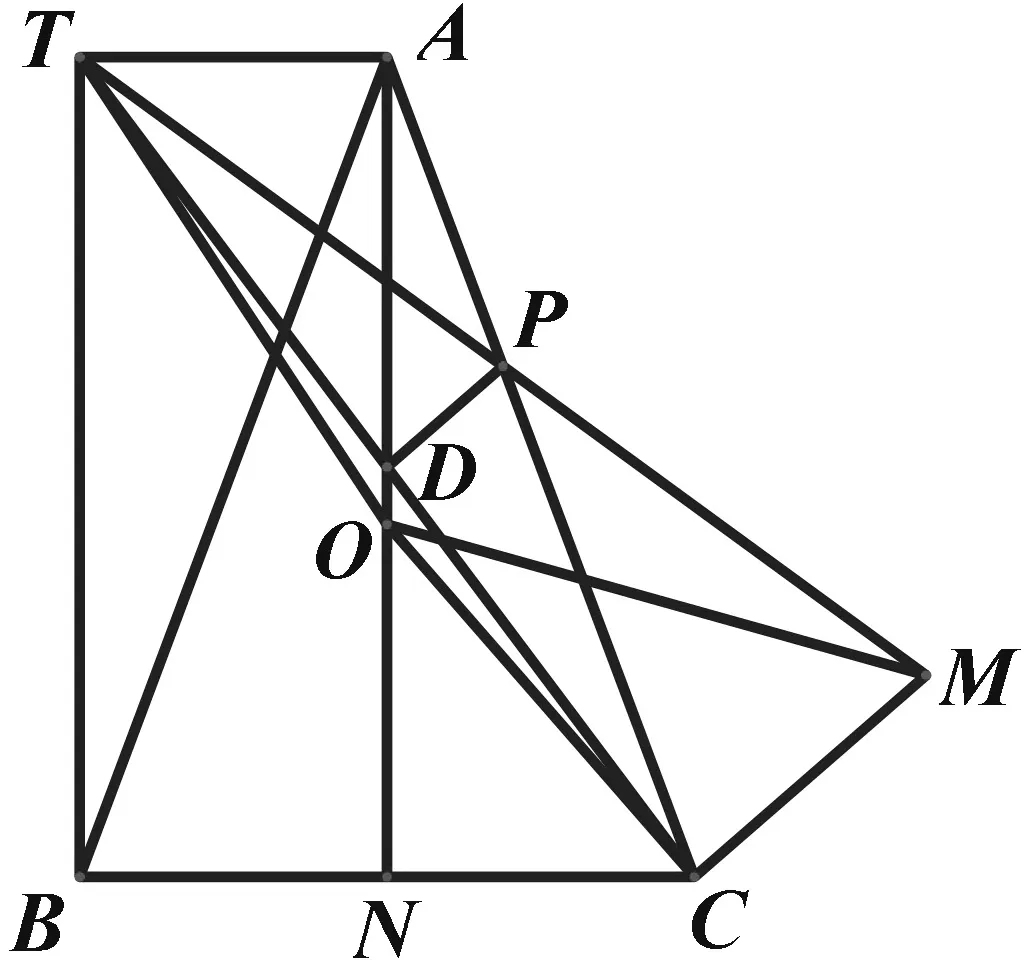
图2

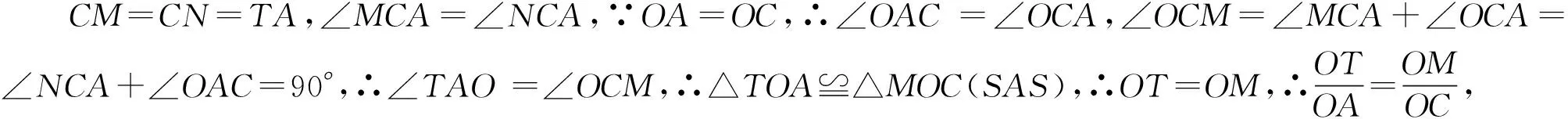
下面我们重点说明第(2)小题第②问.

由(1)可得点D是TC中点，问题转化为证明点P是TM中点即可．而证明中点，往往有构造全等三角形、等量代换、等腰三角形“三线合一”、构造三角形中位线等“基本思路”，由于本问是证明中位线，故“基本思路”只有前面三种.

基本思路一 构造全等三角形

由于TP、PM分别是△TAP、△MCP的边，而两三角形大小不同，故考虑使用“割补法”构造全等三角形来证明TP=PM.

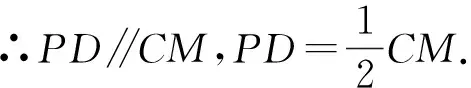
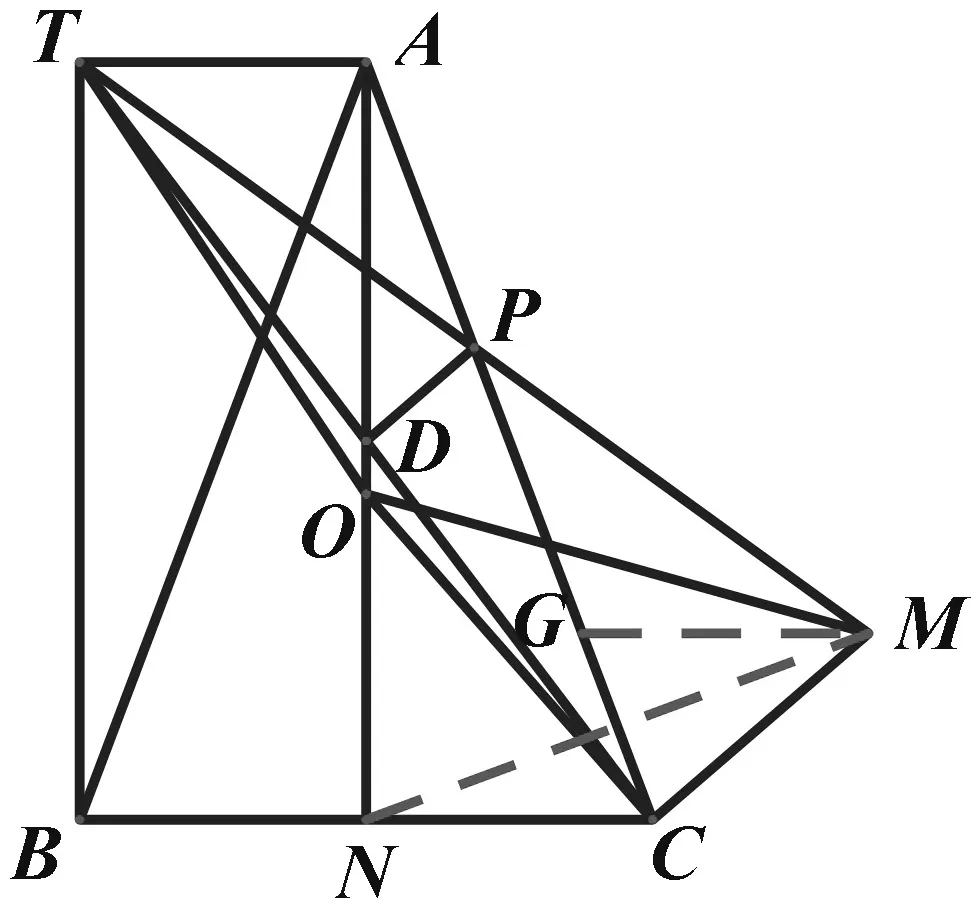
图3

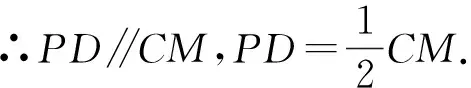
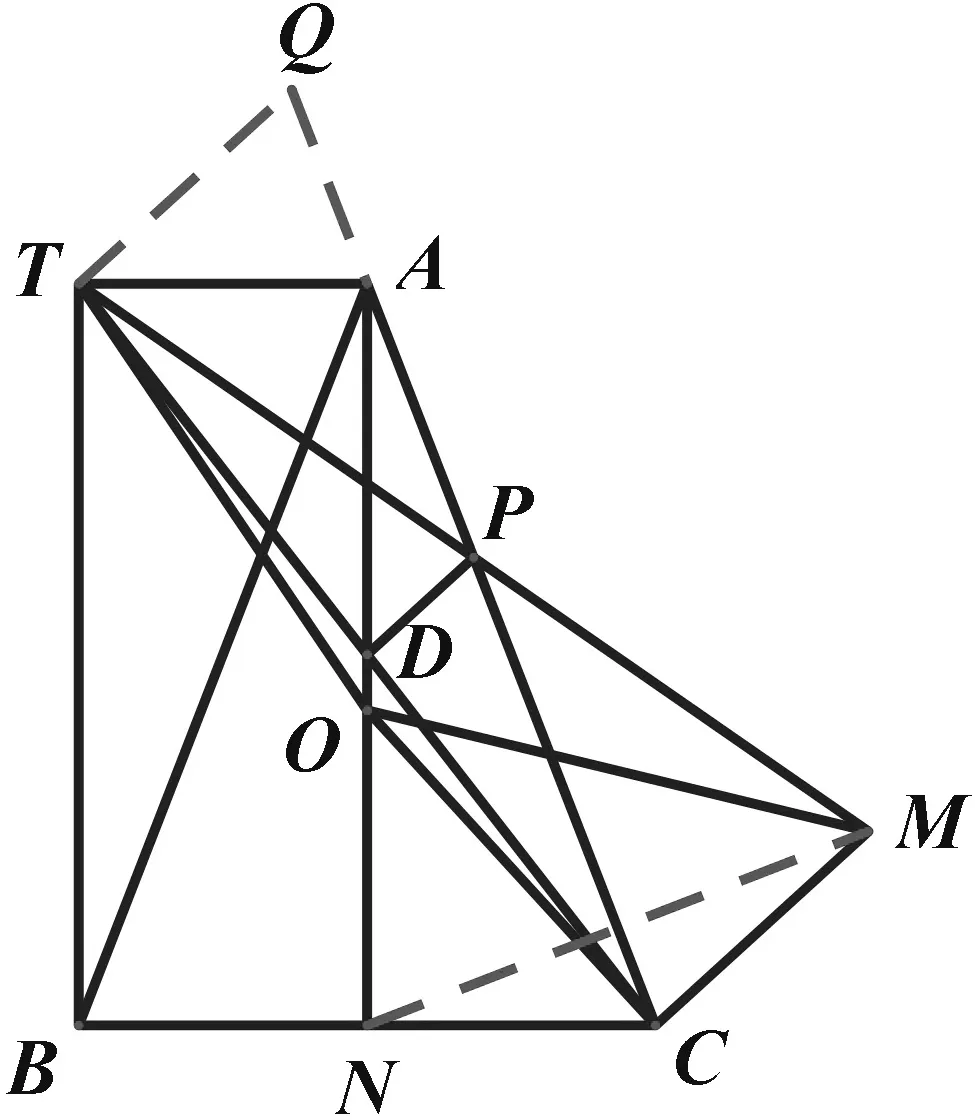
图4

基本思路二 等量代换

由题中“对称”这一条突出条件，能立即发现PM=PN，而要证明TP=PM，可考虑利用等量代换证明PT=PN即可.

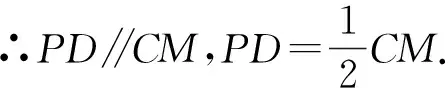
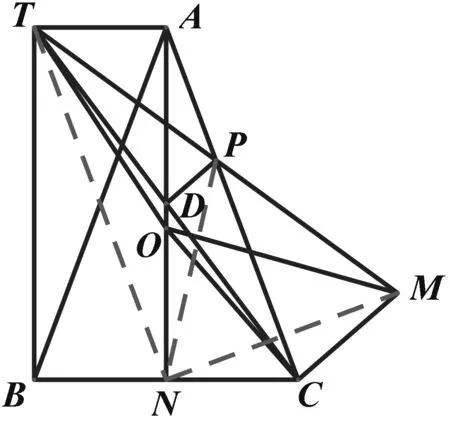
图5

基本思路三 等腰三角形“三线合一”

要证点P是TM的中点，观察到△OTM是等腰三角形，故考虑连接OP，利用等腰三角形“三线合一”证明OP⊥TM即可.

解法4：如图6，连接OP，由①有△TOM∽△AOC，∴∠PMO=

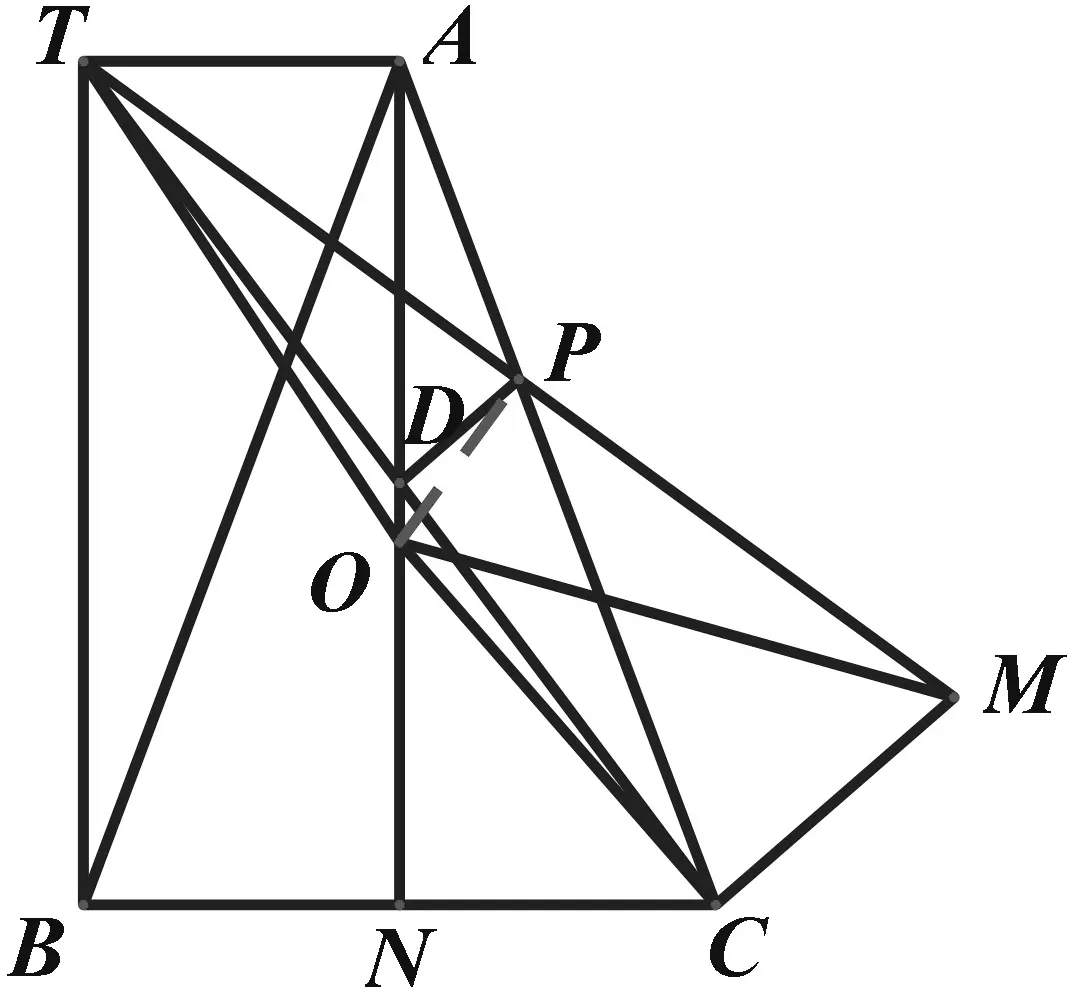
图6

解法5：如图7，连接OP，由①有△TOM∽△AOC，∴∠PMO=∠PCO，∵∠PHM=∠OHC，

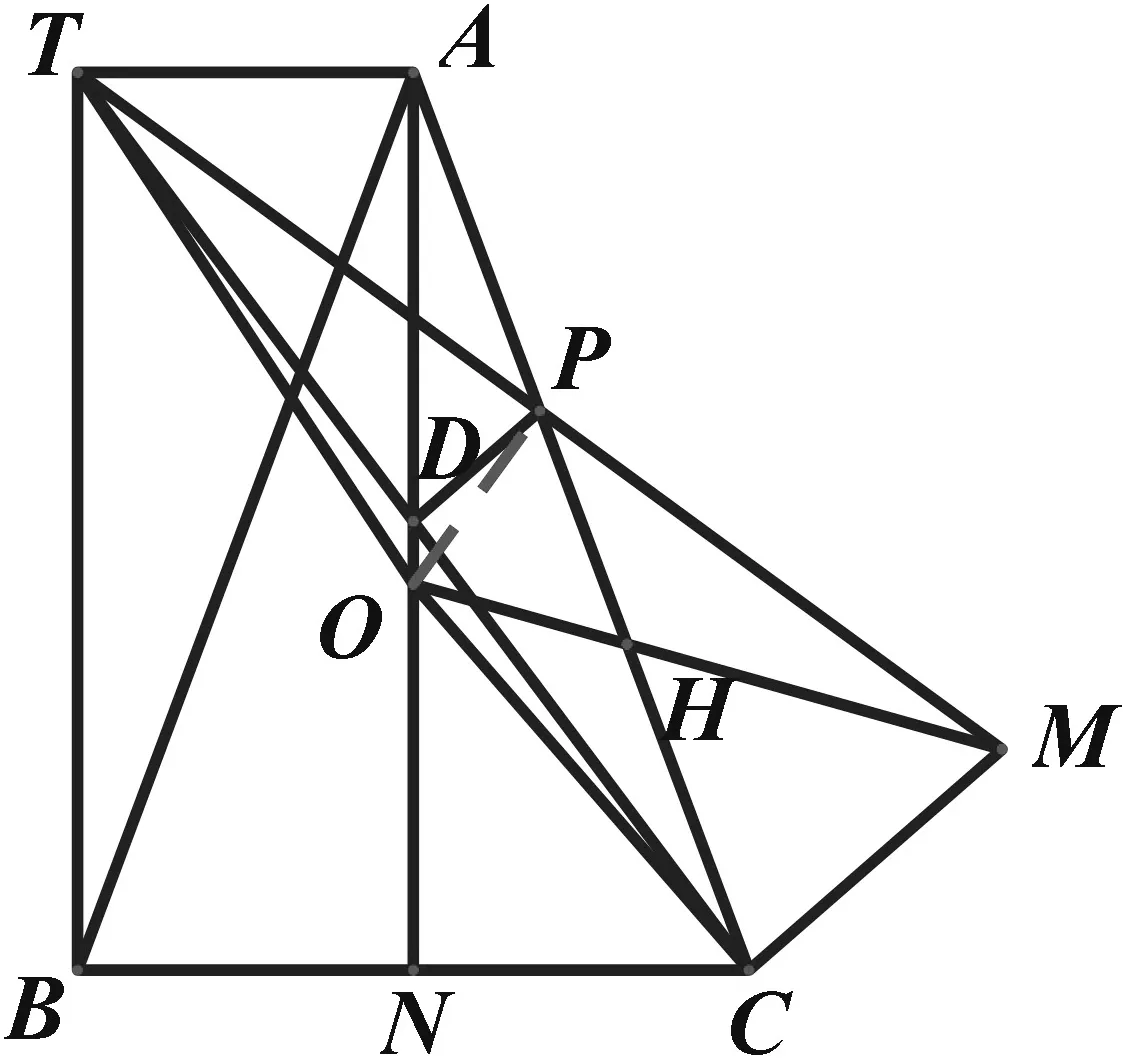
图7

以上两种解法均是在四边形PMCO中求证的，在四边形PATO也有类似的两种解法，在此不一一赘述.

通过以上说明我们可以发现：“基本思路”是依据基本定理、重要结论而形成的，是提升数学能力，发展数学核心素养的重要环节，利用“基本思路”解题符合理性思维的特征，有利于优化数学思维品质．在教学中，教师加强“基本思路”的引导，在练习中，学生注重利用“基本思路”思考，在深刻理解“基本思路”后，辅助线的添加就不再是天马行空仅凭感觉的，而是水到渠成、合情合理的，中考几何压轴题的突破也就变得顺理成章了.