截卵形弹丸斜穿甲均质薄靶剩余速度的理论分析

巨圆圆，杜志鹏，张 磊

（海军研究院，北京 100161）

0 引言

半穿甲战斗部对舰船目标主要通过战斗部穿甲进入目标内部一定距离后，再起爆装药，对目标内部结构、设备和人员进行毁伤。由于舰船目标的灵活性，战斗部往往以一定的入射角侵彻目标，而且不同着靶位置处目标的厚度也有一定差异。因此，研究战斗部斜穿甲后的剩余速度对提高反舰战斗部毁伤能力具有重要意义。

薄板在弹体冲击下的破坏模式主要有剪切冲塞和花瓣开裂两种[1]：钝头弹体冲击下，薄板的破坏模式主要是剪切冲塞；尖头弹体冲击下，薄板的破坏模式主要是花瓣型破坏。Zaid 等[2]通过假设靶板材料破坏后的位置得出轴向冲量的表达式，应用动量守恒原理得到弹体穿过靶板后的速度损失，然而基于动量守恒原理的分析忽略了靶板强度，所以在弹速较低时误差较大。Landkof 等[3]采用能量守恒原理进行正穿甲理论分析，认为靶板吸收的能量分别以裂缝扩展、花瓣弯曲以及靶板碟形凹陷的形式耗散掉。目前，对截锥形和尖形弹丸正侵彻薄靶的研究相对比较多[4-6]，而对截卵形弹丸斜侵彻薄靶的研究主要集中于实验和数值模拟方面。段卓平[7]利用模拟实验弹体对均质靶和单层加筋结构靶进行了穿甲实验，并建立了弹丸侵彻加筋结构靶的终点弹道计算模型。刘晓明等[8]对加筋板架和均质靶板抗截卵形动能弹穿甲进行了数值模拟研究，分析了靶板屈服应力、硬化模量、厚度和弹丸初始速度对弹丸剩余速度和靶板能量吸收的影响。

对截卵形弹丸斜穿甲均质薄靶的过程进行了数值模拟，靶板破口形貌和弹丸剩余速度均与实验结果相符，表明数值模拟方法和材料参数是合理的。在此基础上，对同一弹丸以不同入射角侵彻不同厚度薄靶的过程进行了数值模拟，得到了弹丸入射角和靶板厚度对弹丸剩余速度的影响。通过量纲分析的方法，分析得到了弹丸剩余速度的理论计算公式，通过验证，理论计算公式具有一定的有效性。

1 截卵形弹丸斜侵彻靶板过程模拟

1.1 有限元计算模型

文献[7]中实验弹为截卵型弹头，弹体长370 mm，弹径105 mm，截顶直径约为20 mm，弹头圆弧半径180 mm，弹重16.06 kg。弹丸有两种材料，外壳采用30CrMnSiNi2A 钢材，弹体内填装密度约为3.15 g/cm3的惰性材料。均质靶板采用921A 钢，厚度为15.2 mm。靶板四周刚性固定，弹丸和靶板之间采用面接触侵蚀算法。弹丸和靶板的有限元模型如图1 所示。

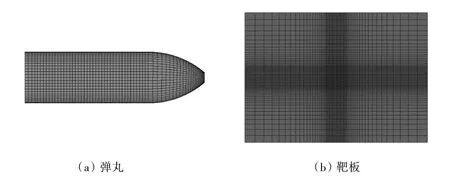
图1 弹靶有限元模型

炸药用弹性材料模型，弹体和靶板采用塑性动态硬化材料模型，在处理材料的破坏失效时，将等效塑性应变作为材料的失效判据，考虑应变率的影响，本构方程采用Cowper-Symmonds 塑性动态硬化材料模型[9]：

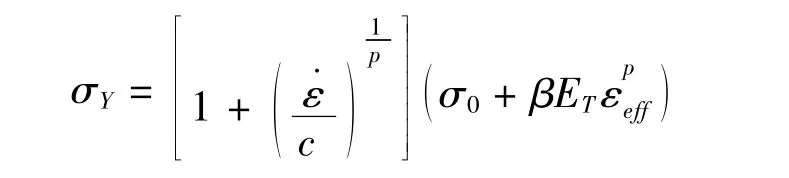
式中，滓0为静态屈服应力为材料的等效塑性应变，滓Y为动态屈服应力，茁为屈服应力强化因子，ET为塑性硬化模量，c、p为材料常数。所用材料参数见表1，其中，籽为材料密度，E为杨氏弹性模量，v为泊松比。

表1 弹靶材料参数

1.2 数值模拟结果与实验结果比较

图2 为弹丸以606.5 m/s 初速侵彻厚度为15.2 mm薄靶后靶板的破口形貌。靶板的主要破坏形式为冲塞型和花瓣型破坏，破口基本呈圆形，弹孔直径和弹丸直径基本相等，与实验现象相符，数值模拟剩余速度为583.30 m/s，与实验结果583.60 m/s 一致[7]。因此，数值模拟中选用的材料参数和计算方法是合适的。

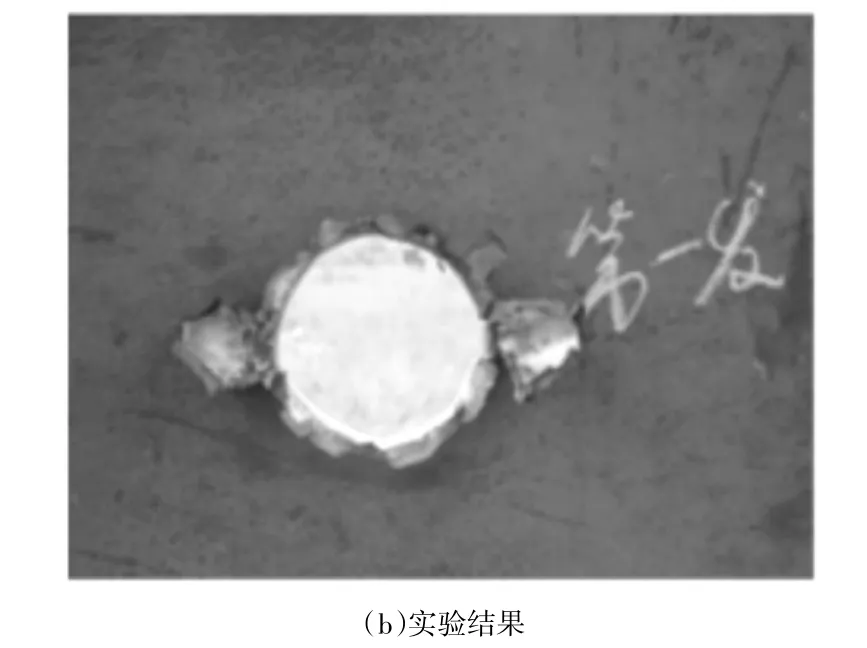
图2 薄靶破口形貌

2 截卵形弹丸斜侵彻薄靶剩余速度量纲分析

截卵形弹丸斜侵彻薄靶后剩余速度的主要影响因素包括：弹丸直径D、弹丸头部半径R、截顶直径d、弹丸密度籽、弹丸初始速度v0、入射角（弹丸速度与靶板法线的夹角）兹；靶板厚度H、薄靶材料的动态屈服极限滓y、断裂应力滓f、断裂应变着f和应变率着觶f。

弹丸剩余速度vr是上述变量的函数，即

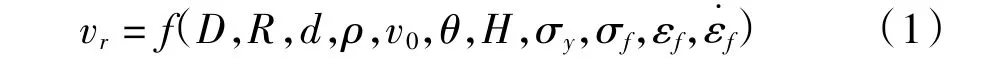
选取D、籽、v0为基本物理量，对上式进行无量纲化，有

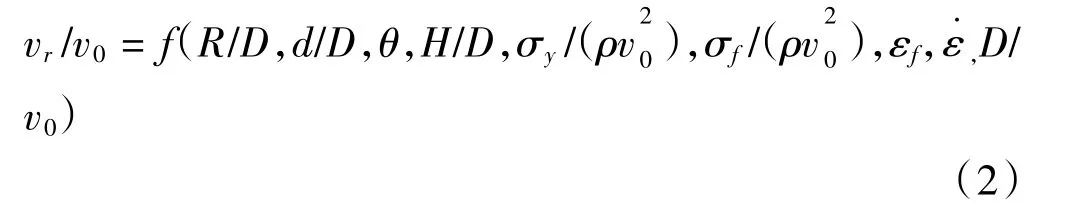
如果模型和原型中弹丸形状、密度籽、初始速度v0以及薄靶材料均保持不变，弹丸初速约为600 m/s，应变率保持不变，则上式可简化为

从上式可以看出，模型和原型中弹丸形状、弹丸密度、初始速度以及靶板材料保持均不变时，弹丸相对剩余速度vr/v0仅与入射角兹和靶板相对厚度H/D两个无量纲量有关。

3 截卵形弹丸斜侵彻薄靶剩余速度理论公式

3.1 入射角及薄靶厚度对弹丸剩余速度的影响

图3 为弹丸剩余速度随入射角和靶板厚度的变化。可以看出，弹丸剩余速度随着入射角和靶板厚度的增大而减小。靶板厚度相同时，入射角越大，剩余速度减小越明显，入射角较小时（<10毅），剩余速度减小缓慢；入射角相同时，剩余速度随靶板厚度增大而明显减小。

图3 弹丸斜侵彻薄靶后的剩余速度

3.2 弹丸剩余速度理论公式拟合

弹丸以不同入射角侵彻不同厚度靶板后的剩余速度曲线，如图4 所示。弹丸剩余速度vr/v0与入射角余弦cos兹基本呈线性关系，对靶板厚度为H= 20.0 mm的情况进行拟合（图4（a）），拟合曲线为

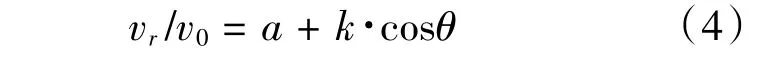
式中，a= 0.86、k= 0.09。

考虑靶板厚度对剩余速度的影响，如图4（b）所示，拟合曲线为

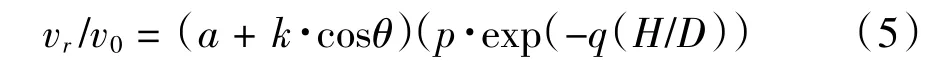
式中，p= 1.09、q= 0.5。

可以看出，弹丸剩余速度随着入射角余弦的减小（入射角增大）呈线性减小，随着靶板厚度增加呈指数减小。另外，数值模拟结果相对拟合曲线分布比较集中，拟合公式和数值模拟结果符合较好。

3.3 弹丸剩余速度理论公式数值验证

为了验证拟合表达式的有效性，对相同弹丸斜穿甲不同厚度靶板进行了数值模拟。表2 为数值模拟结果和理论预测结果的比较，可以看出，误差在1%以内，说明拟合公式具有一定的有效性。

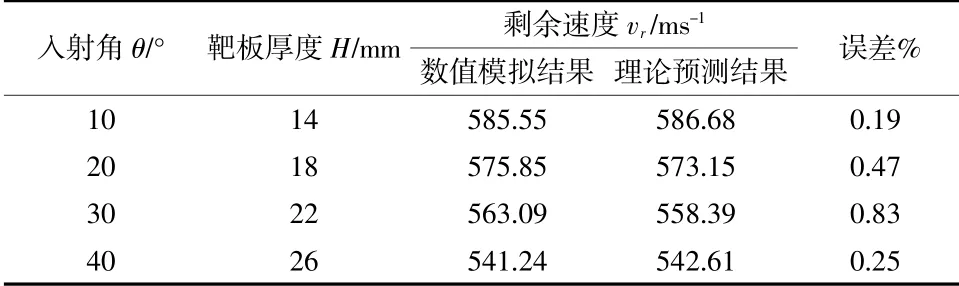
表2 数值模拟结果和理论预测结果比较

4 结语

对截卵形弹丸斜穿甲均质薄靶的过程进行了数值模拟，靶板破口形貌和弹丸剩余速度均与实验结果相符，表明数值模拟方法和材料参数是合理的。在此基础上，对同一弹丸以不同入射角侵彻不同厚度薄靶的过程进行了数值模拟，得到了弹丸入射角和靶板厚度对弹丸剩余速度的影响。通过量纲分析的方法，分析得到了弹丸剩余速度的理论计算式，通过验证，理论计算式具有一定的有效性。