电磁超声回波信号降噪方法研究

张延兵，许世林，顾建平，张 颖，张 维

（1.江苏省特种设备安全监督检验研究院，江苏 南京 210000；2.常州大学 环境与安全工程学院，江苏 常州 213164；3.东北石油大学机 械科学与工程学院，黑龙江 大庆 163318）

0 引言

电磁超声检测是无损检测领域出现的新技术，该技术利用电磁超声传感器（Electromagnetic Acoustic Transducer，EMAT）能够实现非接触检测。超声波源直接在检测对象中产生，回波振幅不受接触压力的影响，对表面粗糙度也不敏感，具有精度高、无需耦合剂、适用于高温检测以及容易激发各种超声波性等优点，因此被广泛应用于多种工业检测中，如测厚、探伤、材料晶格结构检测及材料应力检测等[1-4]。但由于电磁超声回波信号弱，为增大信号，往往采用较高的增益值，在增大回波缺陷信号的同时也增大了噪声信号，这导致信号的信噪比远远低于压电超声信号。对于这个问题，目前多采用硬件电路降噪，对于回波信号降噪软件处理方法的研究并不多[5，6]。硬件降噪有一定的效果，但由于使用环境多样以及自动化快速检测的需要，还需要对缺陷信号降噪处理方法进行研究。因此，针对电磁超声检测过程中的回波信号含噪问题，采用小波阈值降噪以及基于经验模态分解（Em原pirical Mode Decomposition，EMD）的小波阈值降噪方法这两种方法对电磁超声信号进行降噪处理，并采用信噪比（Signal-Noise Ratio，SNR）及均方根误差（Root Mean Squard Error，RMSE）这两个指标作为降噪优劣的评价标准，前者越大越好，后者越小越好，从而探究最有效的电磁超声信号降噪处理方法，以期提升电磁超声检测技术在工业应用时信号识别准确率。

1 降噪方法原理

1.1 小波阈值降噪原理

小波降噪阈值降噪是基于小波分解方法进行的。首先，需要选择合适的小波基和分解层数来分解噪声信号，得到了不同的低频部分及高频部分，如图1 所示。噪声信号往往包含在d1、d2、d3中，小波阈值去噪是按一定的阈值规则选取阈值后，再处理小波分解系数，最后重建一些处理后的系数，得到去噪信号[7]。

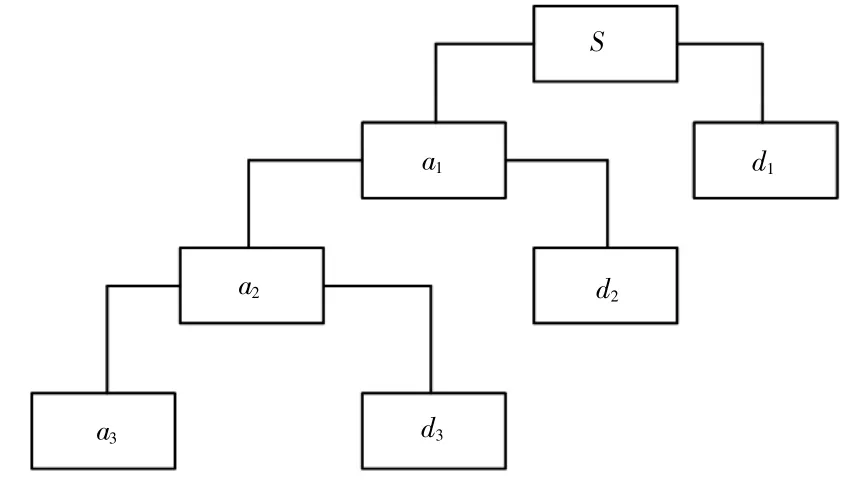
图1 小波分解

目前常用的阈值主要有4 种：rigrsure 阈值、sqt原wolog 阈值、heursure 阈值和minimax 阈值。在决定阈值规则种类后，需要根据待处理信号确定阈值重调方法，有“one”，“sln”，“mln”3 种。阈值判定函数有硬阈值及软阈值两种。

1.2 EMD 原理

EMD 也是将信号分解成相互独立的不同成分，与小波分解及傅里叶变换不同的是其不需要基函数。主要依靠自身在时域上的信号特征进行分解，具有一定的自适应性，适用于不同类型的信号分解。分解得到的不同的imf 分量中的高频分量通常被视为噪声，剔除这些成分之后进行重构达到降噪的目的，然而，这些分量中容易出现模态混叠的现象，因此提出了集合经验模态分解（Ensemble Empirical Mode Decom原position，EEMD）。EEMD 的主要原理是将白噪声添加到信号中形成新信号，然后执行EMD 分解，以获得imf 分量，然后继续添加新的白噪声，重复分解，最终将得到的imf 分量做平均[8]。EMD 和EEMD 用于分解信号，然后使用小波阈值对分量进行去噪。

2 电磁超声信号降噪效果对比

由于使用实际电磁超声检测信号无法获得真实不含噪信号，因此此处分析釆用对比处理后信号有用成分幅值及无回波位置信号平稳性作为对比方案。含噪信号釆用实际电磁超声回波信号，使用超声波标准试块CSK-I-A，将传感器放置在试块上方，对准试块圆弧的圆心，测量100 mm 圆弧，微微调整使得波形出现，传感器测试方法如图2 所示。测量过程采用的自发自收模式，记录下回波波形，如图3（a）所示。对波形进行FFT 变换,得到频域图如图3（b）所示。为了便于展示，将频域图的纵坐标幅值归一化，归一化处理公式如下：

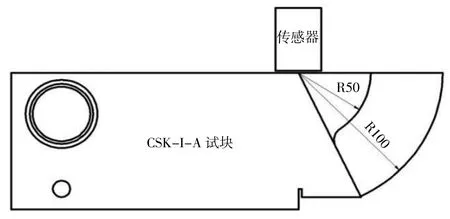
图2 传感器测试实验

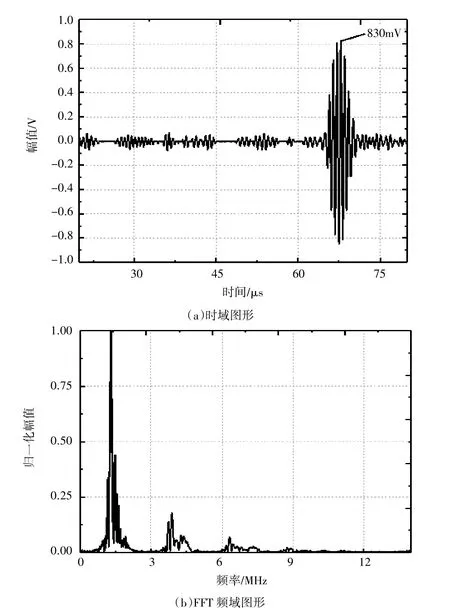
图3 实际含噪电磁超声信号

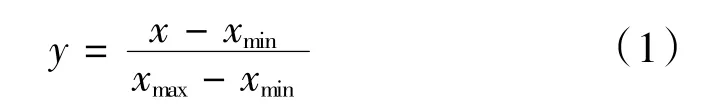
式中x为原始值，y为归一化后的值。后续使用两种方法分别对该波形进行降噪处理。

2.1 基于小波阈值降噪方法评价分析

图4（a）是使用sqtwolog 和minimax 阈值进行小波阈值降噪处理后的信号，使用“db4”小波，分解为4层，使用“mln”重调方法和软阈值函数。图（a）中显示，2 种阈值均能很好地去除信号中的噪声，使用mini原max 阈值时对信号造成的损失最小，信号幅值仍有760 mV，大于使用sqtwolog 时的740 mV，仍能保持较好的信号幅值。图4（b）显示，在处理后的信号中高于3 MHz 的部分被去除，保留了激发频率附近区间的信号成分。说明该方法保留低频率成分，去除高频率成分。使用minimax 阈值时，信噪比SNR 和均方根误差RMSE 的值分别为8.7582 和0.8158，而使用sqtwolog阈值规则时，信噪比SNR 和均方根误差RMSE 的值分别为7.1590 和0.9807，进一步表明使用minimax 阈值规则时，信号的降噪效果更好。

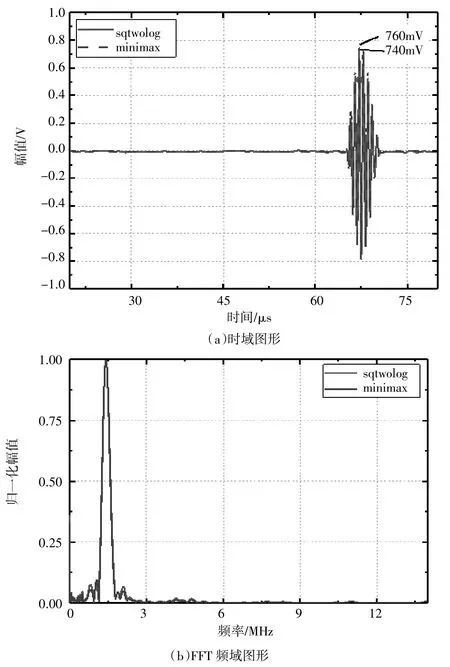
图4 不同阈值方法小波阈值降噪处理后的信号

2.2 基于EMD 和EEMD 的小波阈值降噪

使用基于EEMD 的小波阈值降噪方法处理后的信号（图5（a）），使用minimax 阈值，其余设定与前文小波降噪一致。图5（a）中显示，此方法能良好地去除信号中的噪声，而且保留了原始信号有用成分，能量没有损失，仍为830 mV。图5（b）显示，该方法相对于前两种，对于不同频率信号的处理效果结合了二者的特点，去除高于3 MHz 的信号成分，也降低了激发频率附近区间的能量。此时降噪后信号的信噪比SNR和均方根误差RMSE 分别为10.2420 和0.6877，相较于小波阈值降噪方法，信号的降噪效果进一步优化。

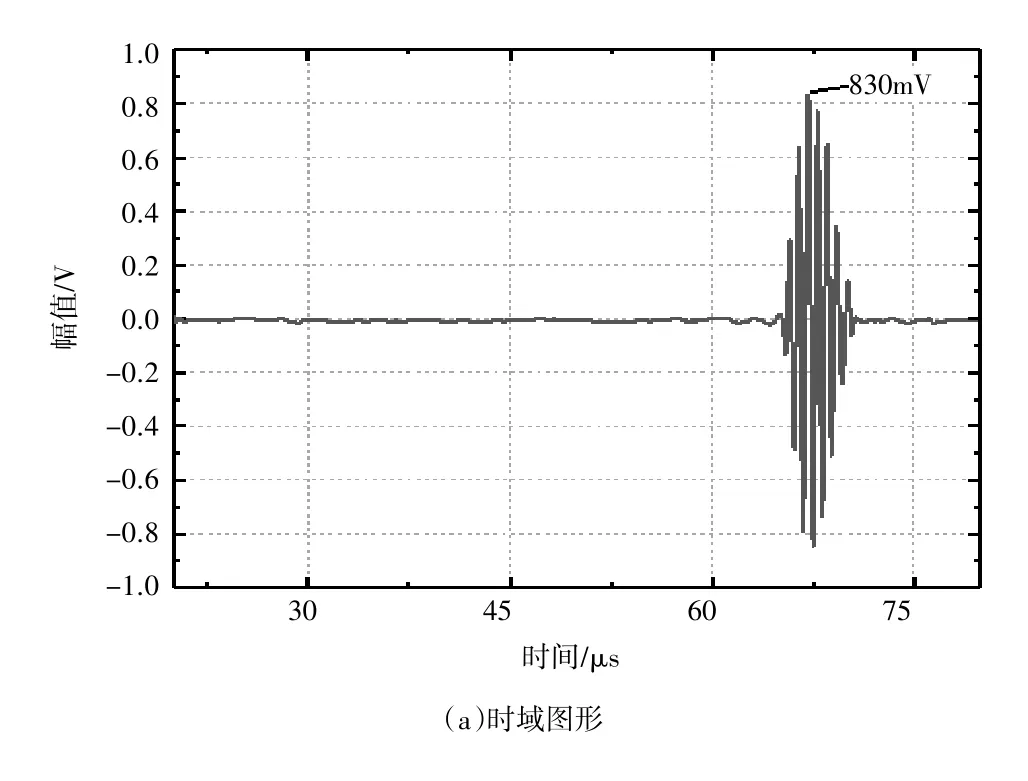
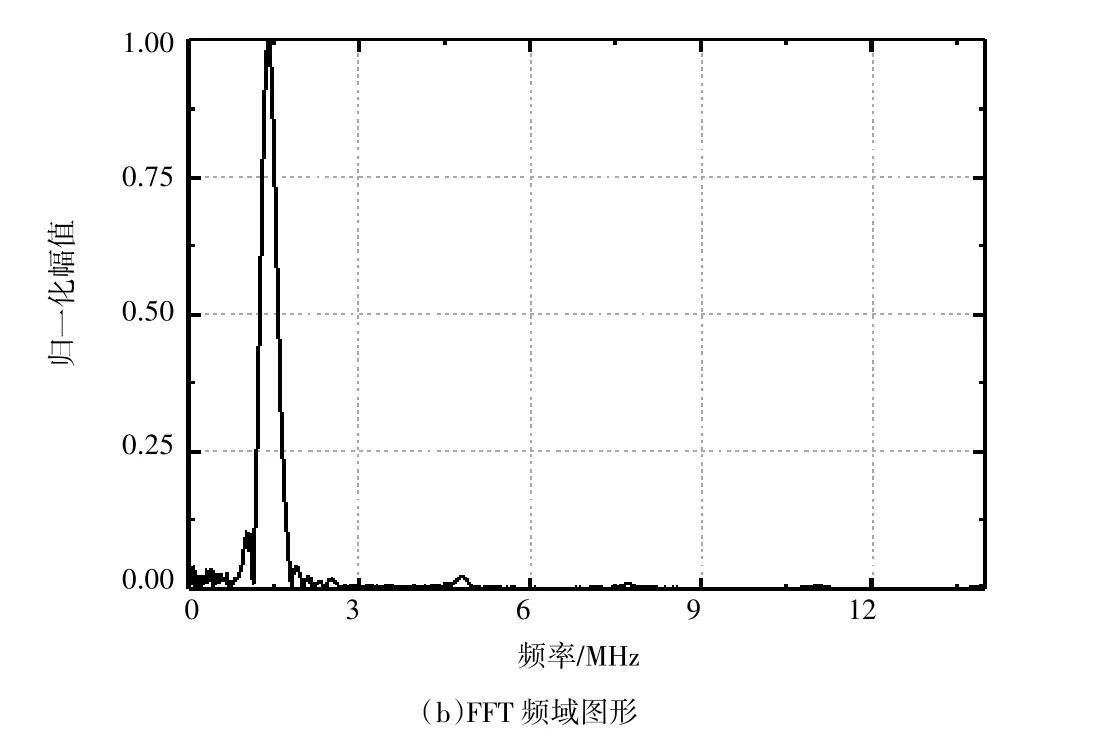
图5 基于EEMD 的小波阈值降噪处理后的信号

通过以上两种方法的对比，可以发现小波阈值方法能够去除电磁超声检测信号中的噪声，但是对信号能量有一定的损失，使用基于EEMD 的小波阈值降噪方法能够良好降噪，并且保留有用成分，便于后期检测的阈值判定。

3 结语

针对电磁超声信号噪声多的问题，使用信噪比及均方根误差两个性能指标评价了两种不同的信号降噪方法，将之应用于实际电磁超声信号降噪效果对比，发现小波阈值降噪方法会造成信号能量损失，而将信号EEMD 处理后，再使用小波阈值降噪方法处理之后得到分量进行重构，能够在保留缺陷回波信号有用成分的幅值不变的同时，很好地消除了信号中的噪声。