分层流中潜艇共振激发内孤波的传播

杨俊彦，杜永成，杨 立

（海军工程大学 动力工程学院,武汉 430033）

0 引 言

1834年8月，John Scott Russell首先发现了在自由表面上传播的孤立波，这是当时传统Airy理论所无法描述的。1895年，Korteweg与Devries发现了孤立波传播满足的非线性模型，描述了内孤波的演化过程。孤立波理论在内波研究中的应用始于20世纪60年代，1966年，Benjamin[1]首先导出了浅水界面波单向传播的KdV 方程，这一方程对小振幅内波的传播误差较小；针对在深海中传播的内波，Benjamin（1967）[2]和Ono（1975）[3]给出了在无限深流体中界面波传播的Benjamin-Ono 方程，简称BO 方程；Joseph（1975）[4]推导了一个有限深度的内波传播方程。以上模型均属于一维内孤波传播模型。Kubota（1978）[5]和Lee(1974)[6]等人提出了中长波内波的传播方程，即ILW 方程。当水深趋于浅水时，其解趋于KdV方程；当水深趋于深水时，其解趋于BO方程。

对海洋中内孤波的传播和演化，人们常用KdV 方程或浅水有限深度方程来研究。由于KdV 方程能很好地处理非线性效应和色散效应之间的平衡，且方程简单，许多水下孤立波传播的数值模型都是基于KdV 理论。Koop 与Butler、Segur 和Hammack 检验了KdV 方程和有限水深方程的有效性，发现即使在KdV 方程的假设条件仅有少量满足的条件下，它仍具有很好的适用性。Shishkina(1994)[7]在热分层水槽中，实验研究了细长拖曳模型共振激发的内孤波，发现激发的内孤波与KdV方程描述的内孤波波形是一致的。

在实际海洋中航行的潜艇，由于潜艇激发的内波幅值较小[8]，大约为10 米量级，高阶非线性影响较小，本文采用KdV方程来研究潜艇激发内波的传播特性。

1 非线性内波的KdV方程模型

1.1 KdV方程内波模型

在Boussinesq近似下，1996年，Lamb和Yan[9]给出了无粘不可压缩流体的二维控制方程组：

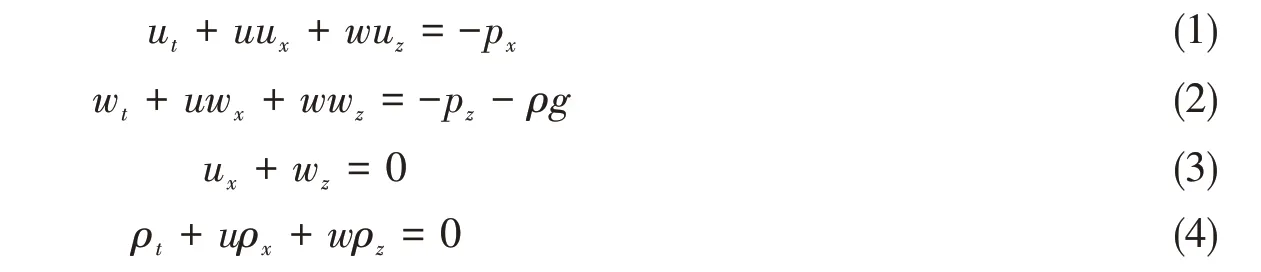
式中：u(x,z,t)、w(x,z,t)分别代表水平与垂向流速；t为时间；g代表重力加速度，正向为垂直向上方向；ρ代表无量纲的密度，相应的有量纲密度为ρ0(1+ρ)；ρ0表示为参考密度；p为无量纲压强，对应的有量纲的压强为ρ0g(H-z) +ρ0p，H代表水的深度。在海底，取z= 0；在z=H处，认为是刚性海面。

在公式（1）与（2）中消除压强p，导出的流函数Ψ(x,z,t)和密度扰动控制方程为[10]

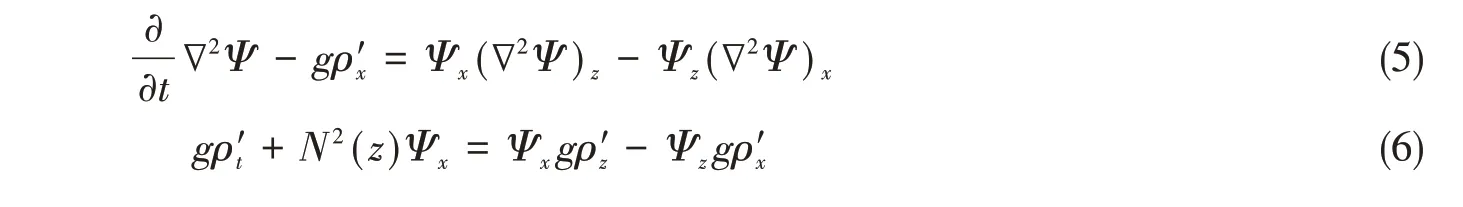
式中，

密度ρ可表示为背景的平均密度与扰动密度ρ'之和，N代表环境的浮频率。对于小振幅长内波，流函数Ψ(x,z,t)可用小参数渐进展开[10]：

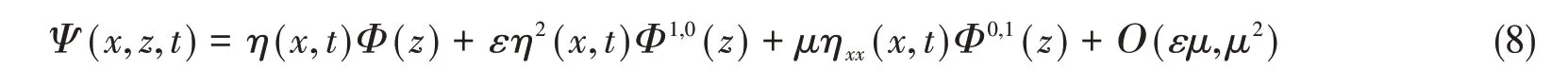
式中，μ=H2/L2，ε代表内波波动振幅与深度之比，η(x,t)为内波的幅值，Φ(z)为内波垂向位移的模态函数，上标（i,j）代表对应于O(εi μj)项的垂直结构函数。将式（8）代入式（5）和式（6），可得求解流函数Ψ(x,z,t)幅值的方程，即EKdV方程[11]：

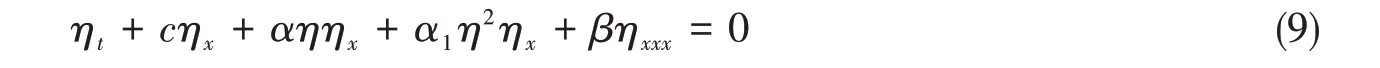
式中，c为长内波相速度（long wave phase speed），α表示平方非线性系数，α1代表立方非线性系数或称高阶非线性系数，β表示色散系数。对潜艇激发的内波，由于波幅较小，可忽略高阶非线性项的影响，当α1=0时，方程（9）变为KdV方程：

内波垂向位移的模态函数Φ(z)可由下式计算[10]：

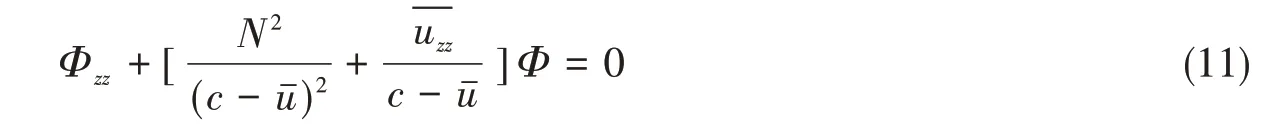
1.2 非线性和频散系数计算

2004年，Grimshaw等[11]给出了公式（10）中非线性系数和色散系数的计算公式：

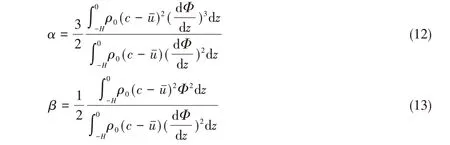
根据蔡树群和甘子钧（1995）[12]在无Baussinesq 近似下的Thomson-Haskell 方法（简称T-S 法）可求解得到Φ(z)的数值解和相速度c。由Φ(z)和方程（12）～（13），可计算得到非线性系数和色散系数。对常系数KdV方程，其理论解为

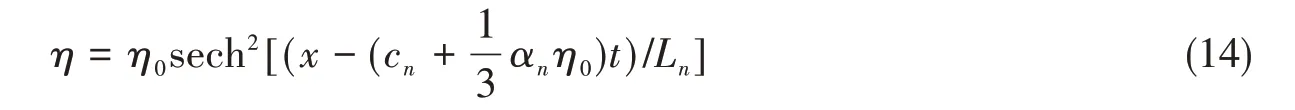
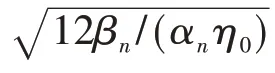
式中，η0为孤立波的振幅。

2 KdV方程数值求解方法

求解非线性KdV 方程的数值解法有多种，如有限差分法和伪谱法（pseudospectral method）等。1965年，Zabusky与Kruskal[15]采用有限差分方法给出了KdV方程的数值解。

本文采用全隐有限差分方法数值求解KdV方程，对式（10）的时间项取

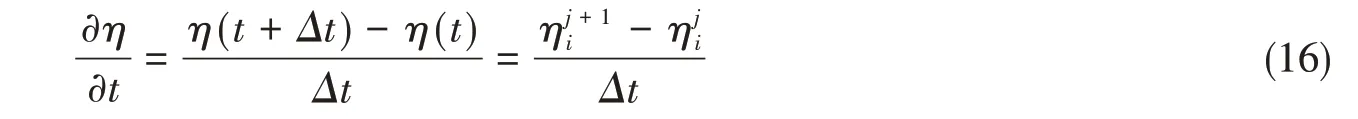
式中，j为时间序号，i为单元序号。式（10）中的一、三阶导数项取

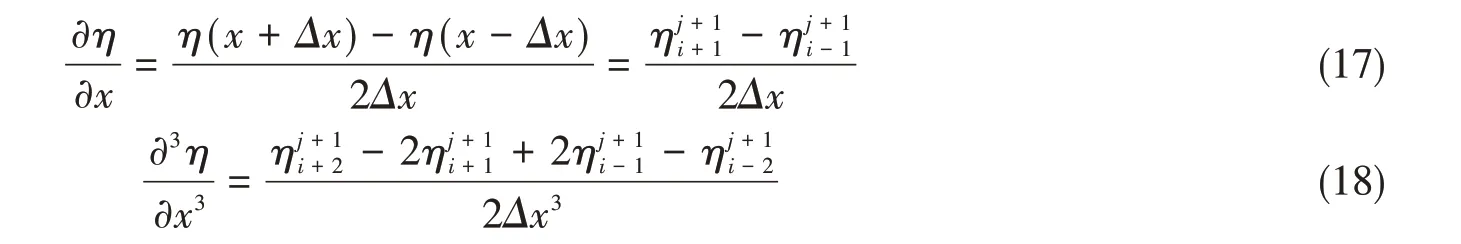
式（10）中的η项取为

将公式（16）～（19）代入式（10），可得KdV方程的全隐式差分格式为

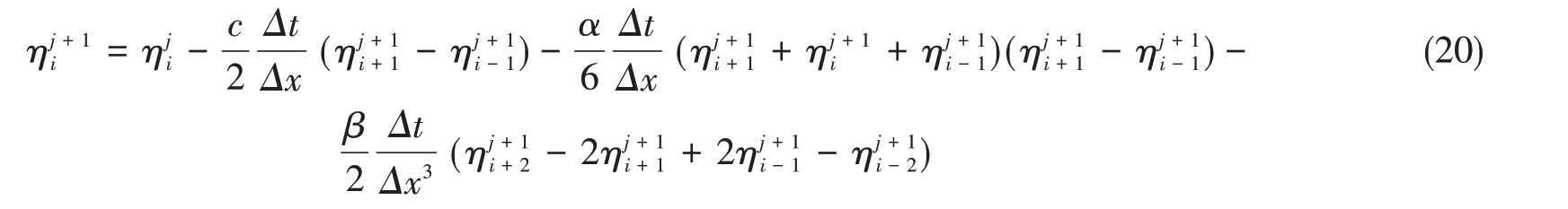
式中，Δt为时间步长，Δx为空间步长。

3 潜艇激发内波的传播

3.1 内波传播模型验证

Shishkina（1996）[7]在热分层环境中进行了孤立波的共振成生实验，实验水槽中的温度、密度和浮频率分布如图1所示。当模型速度与第二模态内波相速度相等时，将产生第二模态孤立波，实验得到的激发内波频率为0.100 6 rad/s。实验测量得到的孤立波波速为V2=0.013 6 m/s，内孤波幅值为η0=0.006 m,内波的特征半倍波宽为L2=0.6 m。

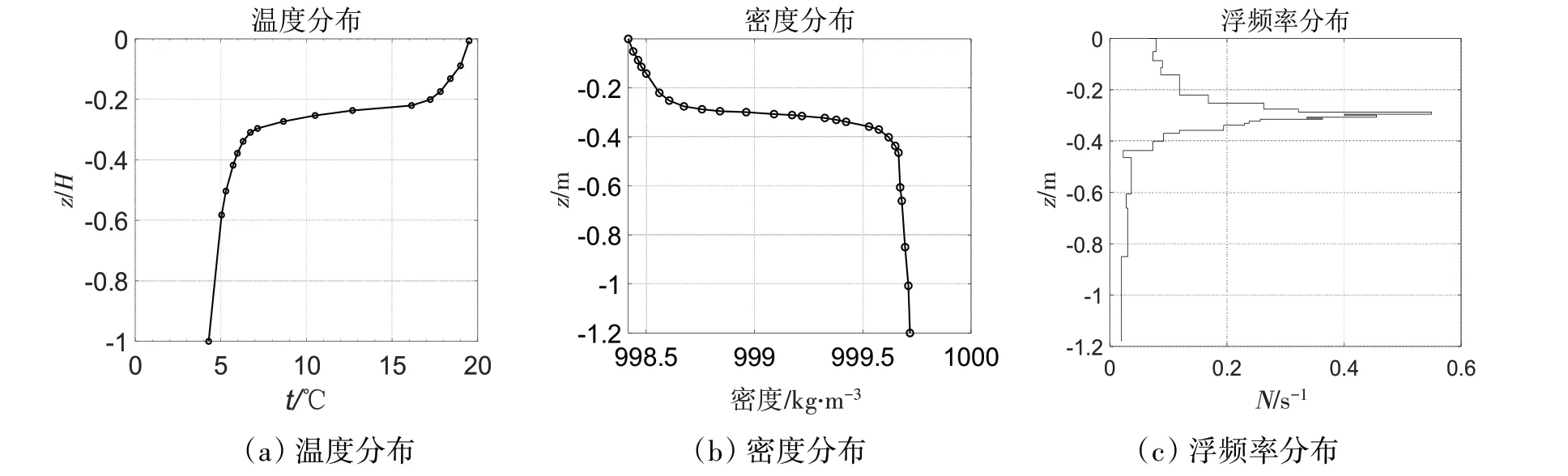
图1 Shishkina（1996）实验的温度、密度和浮频率分布Fig.1 Distribution of temperature,density and buoyancy frequency in Shishkina's（1996）experiment

根据内波理论可计算出在该实验条件下的前3模态的水平波数kh为1.282、7.367 7、10.268 rad/m,相速度ch为0.078 4、0.013 6、0.009 8 m/s，如图2 所示。计算得到的各模态内波波函数见图3。根据内波KdV 方程非线性系数和色散系数计算公式（12）和（13），可计算得到内波第一至第三模态非线性系数α分别为0.025、1.68和0.071 6,色散系数β分别为0.017 6、0.000 232和0.000 155。

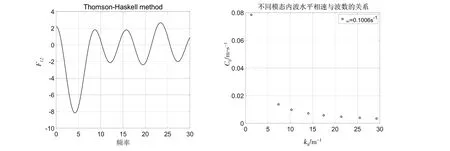
图2 由TH方法计算得到的内波水平相速与波数的关系Fig.2 Relationship between horizontal phase velocity of internal wave and wave number calculated by TH method

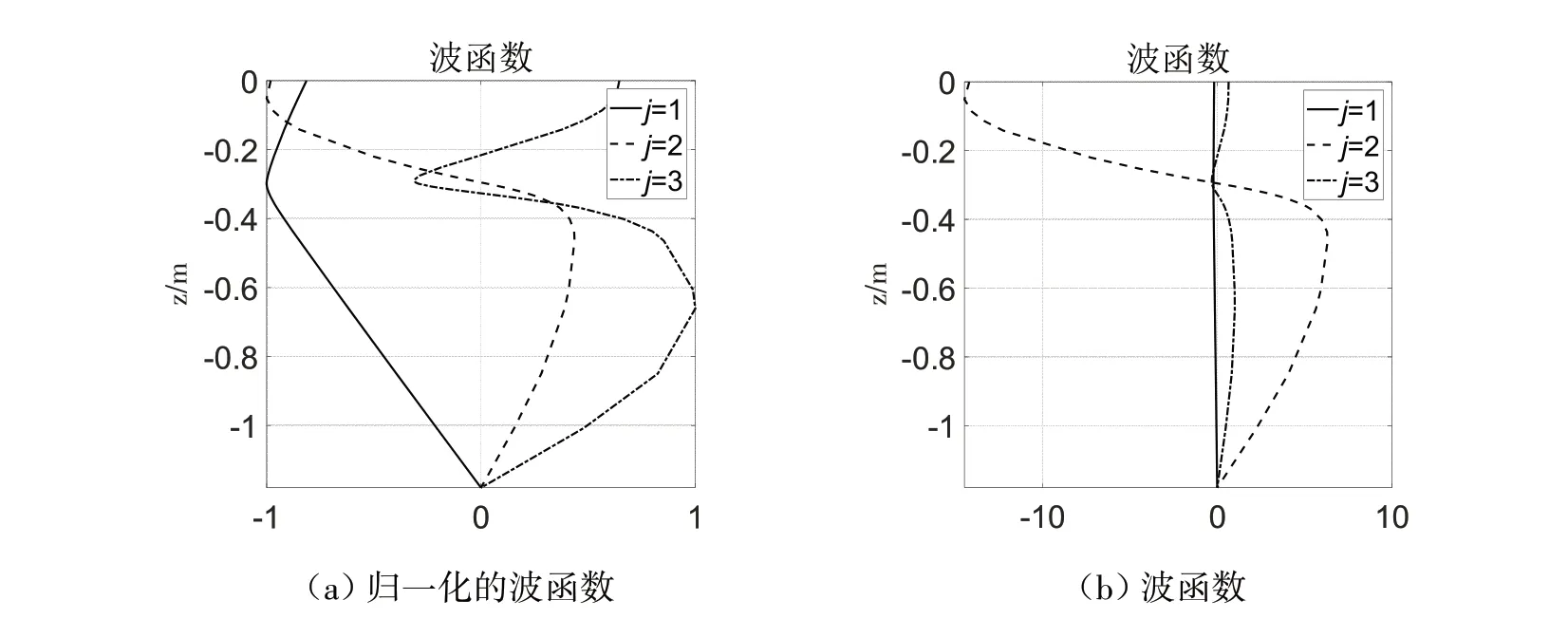
图3 由TH方法计算得到的内波波函数Fig.3 Wave function of internal wave calculated by TH method

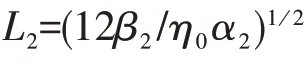
3.2 内波的传播计算与讨论

对实验激发的第二模态内孤波，计算得到非线性系数α=1.68,色散系数β=0.000 232。由KdV 方程的孤波解，可给出初始时刻的孤波波形，利用KdV 方程计算可得到内波随时间和空间的演化。图4和图5为不同时刻激发的第二模态内孤波的空间分布。由图可见，在一定初始幅值条件下，内孤波随时间幅值逐渐增大，在140 s 时内波幅值为0.006 5 m,与实验在同时刻测量得到的内波幅值0.006 m 相比，基本一致，误差为8.33%，说明利用KdV方程可以较为准确地模拟内波幅值随时间的演化。

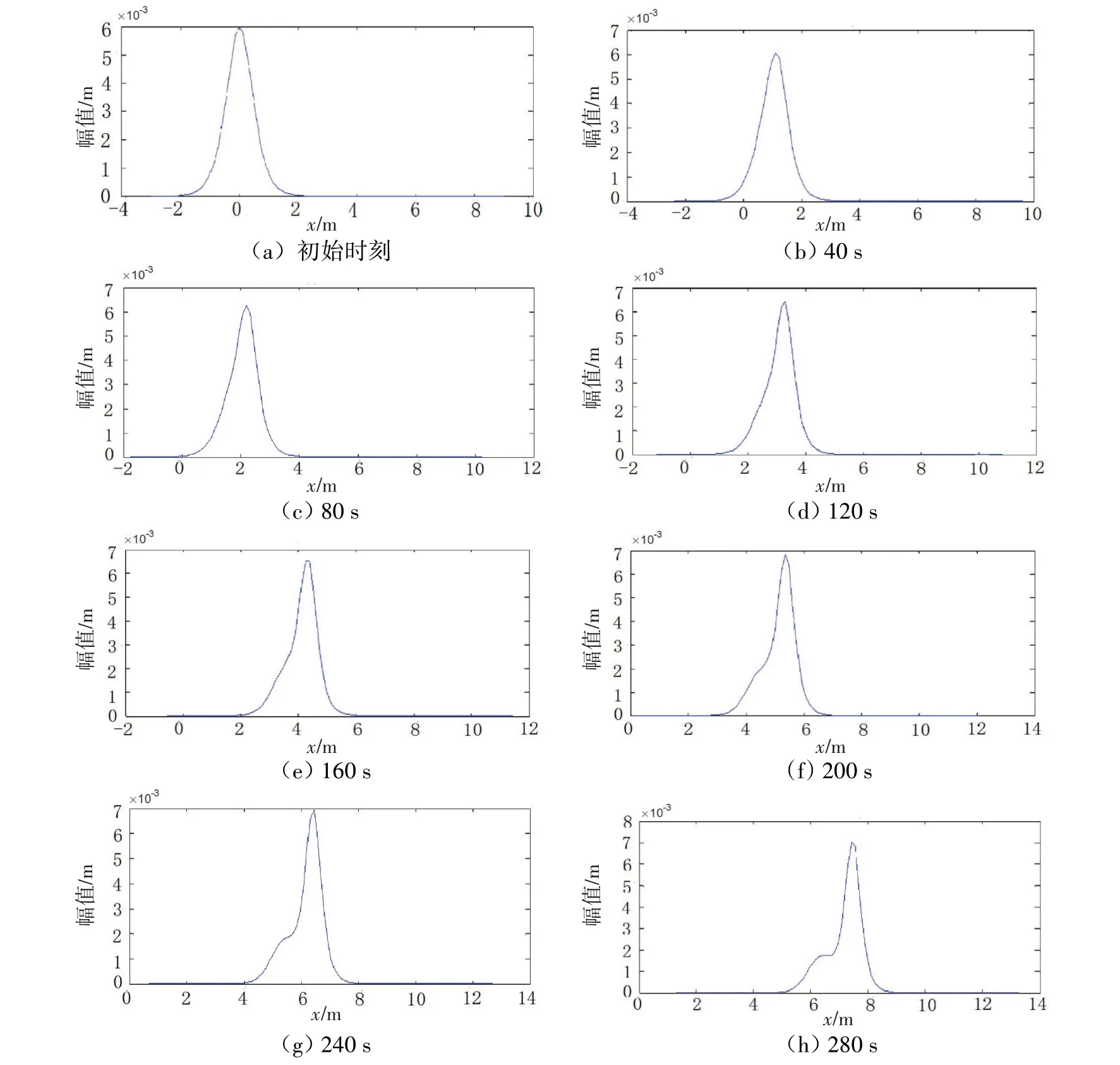
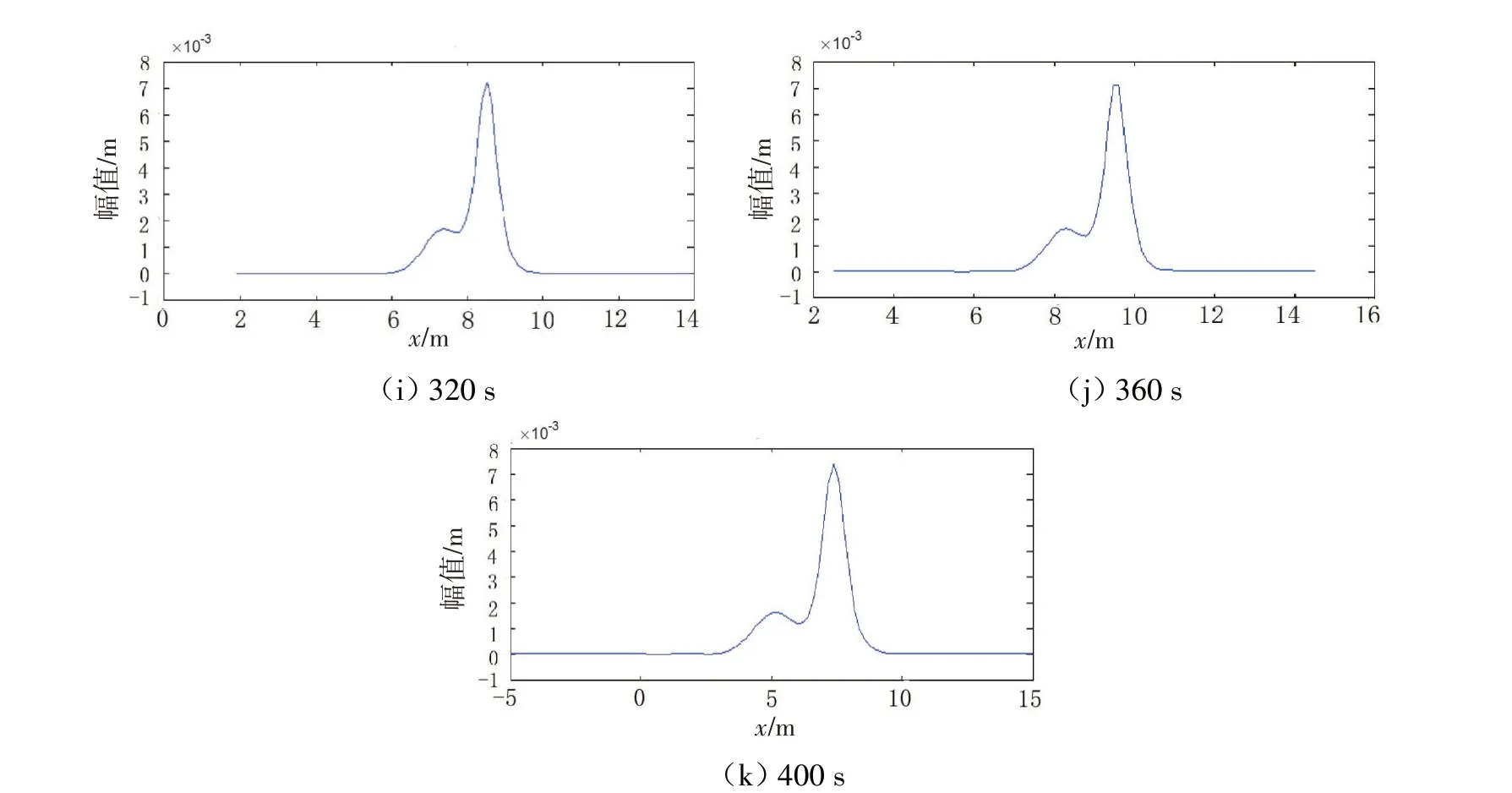
图4 不同时刻内孤波的空间分布Fig.4 Spatial distribution of solitary waves at different times

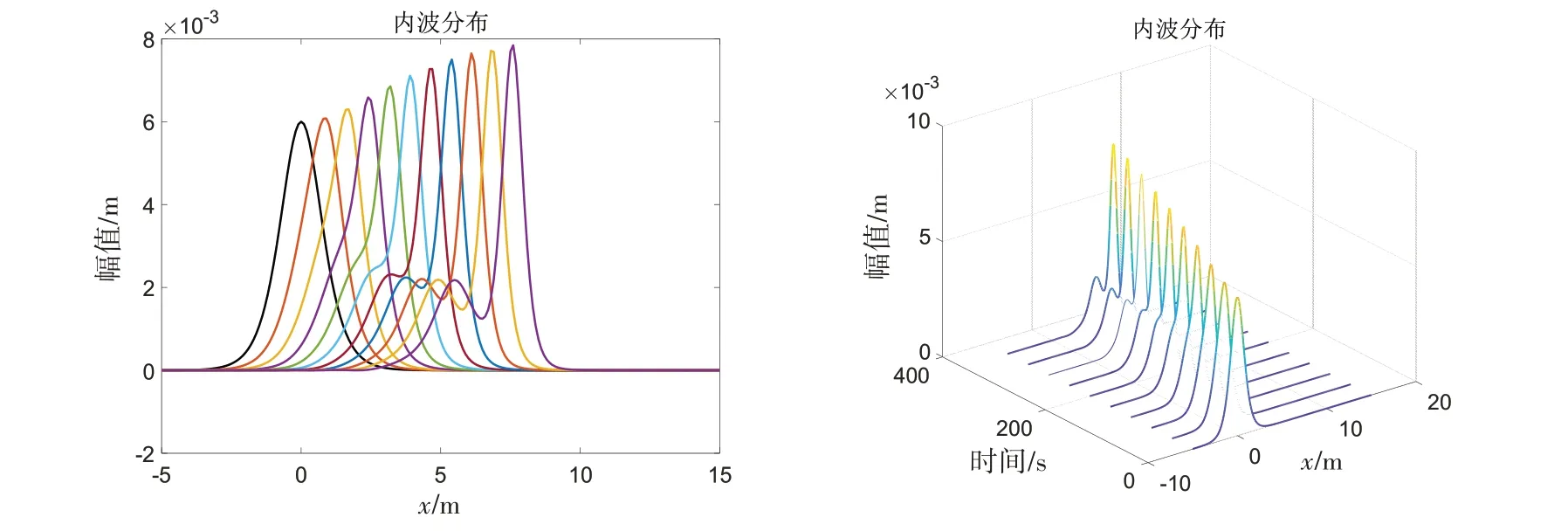
图5 内孤波随时间空间的演化Fig.5 Evolution of solitary waves with time and space

对激发的第一模态内波,由计算得到非线性系数α=0.025,色散系数β=0.017 6，利用KdV 方程计算可得到内波随时间和空间的演化。图6和图7为第一模态内波随时间与空间分布。由图可见,对初始幅值为一定值的内孤波，随着时间的演化，内孤波的幅值逐渐减小，并产生色散效应，与实验观测结果一致，如图8 所示[14]。对第三模态内波，由于非线性效应较弱，色散效应相对较强，内波的时间空间演化规律与第一模态内波类似。

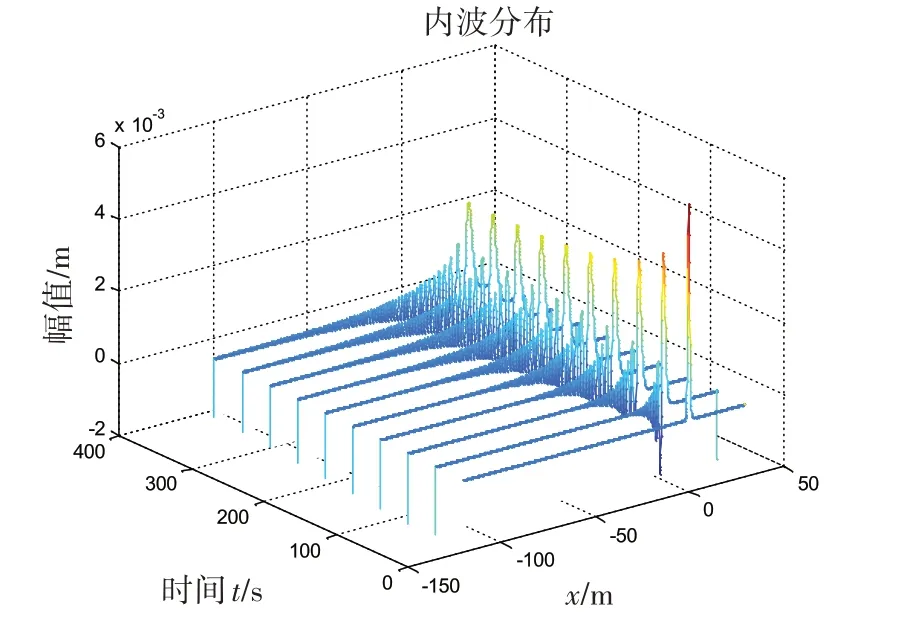
图6 内波随时间空间的演化Fig.6 Evolution of internal waves with time and space

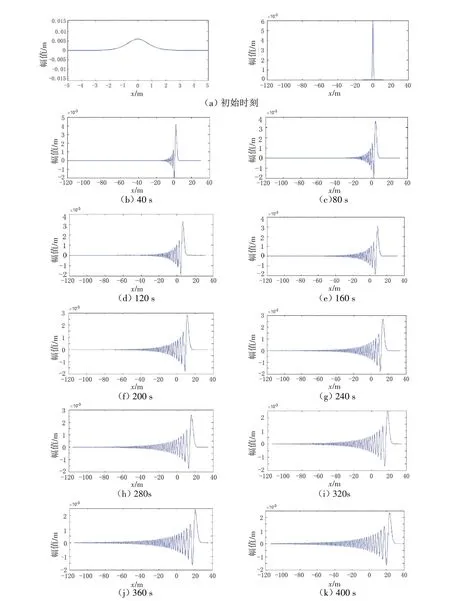
图7 不同时刻内波的空间分布Fig.7 Spatial distribution of internal waves at different times

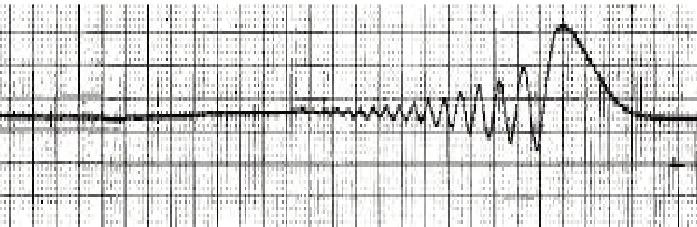
图8 Koop等实验得到的色散内波波列[14]Fig.8 Dispersiver wave train obtained by Koop et al[14]

4 结 语

当潜艇航速与内波各模态的水平波速相等时，潜艇运动将共振激发内孤波。本文考虑色散效应、非线性效应的影响，建立了潜艇内波传播的非线性KdV 数学模型，采用TH 数值方法求解内波各模态的波函数，由已知的当地浮频率计算出内波非线性KdV 数学模型中的色散系数和非线性系数。采用有限差分方法求解KdV 方程，获得了潜艇内波的传播规律。利用前人研究得到的实验数据对潜艇激发的内孤波的传播进行了验证，计算得到的内波传播相速度和内波幅值与实验测量结果的误差均小于20%，说明KdV模型能有效描述潜艇激发的内孤波的传播。

本文采用了无粘不可压缩流体二维控制方程研究潜艇激发的内孤波的传播。由于潜艇激发的内波通常是三维的，下一步将进一步开展潜艇激发三维内波的传播规律研究。