考虑表面粗糙度与轴瓦变形的水润滑轴承动力特性系数计算

冷子珺，吕芳蕊，焦春晓，塔 娜，饶柱石

（1.上海交通大学 a.振动、冲击、噪声研究所；b.机械系统与振动国家重点实验室，上海 200240；2.河海大学机电工程学院，江苏 常州 213022）

0 引 言

船舶推进轴系的支撑特性对轴系动力学性能具有重要影响：轴系中各滑动轴承的动力特性系数会影响轴系的临界转速、转子涡动振幅和推进轴系的稳定性等等[1]，并且在进行轴承-转子系统动力学分析时，轴承的动力特性系数是必要的边界条件[2]。推进轴系的各轴承中，水润滑艉轴承的运行工况最为恶劣：悬伸在船体外的螺旋桨导致轴颈在轴承中倾斜，造成水膜承载力的巨大损失；加之水的粘度低，艉轴承中的水膜必须极薄才能提供足够的承载力，以至于艉轴承运行在混合润滑(mixed lubrication,ML)状态[3]——表面粗糙度对轴承特性有着不可忽略的影响[4-5]。与此同时，艉轴承轴瓦一般为非金属柔性材料，在巨大的承载压力下轴瓦极易变形，这将改变艉轴承内的水膜厚度与压力分布，从而影响轴承特性。由于上述原因，建立在光滑刚性轴承基础上的流体动力润滑理论(hydrodynamic lubrication,HL)难以满足水润滑轴承的动态特性分析需求，需要专门对水润滑轴承的动力特性系数进行研究。

目前，国内外学者已经进行了大量的相关研究。为了考察弹性变形对轴承动力特性的影响，研究者们利用弹性流体动力润滑(elastohydrodynamic lubrication,EHL)理论进行了相关研究。Jain 等[6]采用一阶摄动法计算了考虑轴瓦静态变形的动力特性系数，发现大偏心率下轴承的刚度阻尼明显减小。但其他学者对Jain 的方法持有异议：Zhang 等[7]认为在利用摄动法推导轴承的刚度阻尼时,仅考虑轴瓦静态变形而忽略轴瓦因轴颈位置摄动产生的动态变形，所得到的刚度阻尼只适用于轴颈微幅振动的情况。相应地，Zhang等[7]采用影响系数法计算了轴瓦动态变形并推导了动力特性系数，发现在高偏心率下考虑动态变形的刚度阻尼明显区别于仅考虑静态变形的情况。Kuznetsov 等[8]和周广武[9]建立了和Zhang 类似的模型，分别用平面应变模型与弹性半无限体理论计算了轴瓦变形。在此基础上，Lahmar等[10]研究了轴颈涡动频率对弹流润滑模型下轴承动力特性系数的影响。Liu 等[11]计算了考虑轴瓦静态变形的水膜刚度，并将水膜刚度与轴瓦结构刚度加权平均作为水润滑轴承的综合支撑刚度。对于非金属柔性轴承，推导动力特性系数时考虑因轴颈摄动产生的轴瓦动态变形明显更为合理。但是上述研究在计算动态变形时均假设变形与压力成正比，这种假设只考虑了轴瓦的刚度效应，仅将稳态时的静力学变形关系沿用到动态分析中，忽略了非金属材料的阻尼特性[12]以及轴瓦惯性的影响。此外，大偏心率下，表面粗糙度对轴承特性的影响同样不可忽略[4-5]，但是弹流润滑模型并不能体现粗糙度的作用。

综上所述，针对艉轴承这样的柔性轴承，相关研究主要集中在轴瓦变形对轴承动力特性系数的影响，忽略了水膜很薄时同样重要的表面粗糙度。与此同时，前人在计算轴瓦的动态变形时仅考虑了轴瓦的刚度效应，忽略了非金属材料的阻尼特性与轴瓦惯性。另一方面，对轴颈倾斜这样的特殊工况，相关研究主要是在动力润滑下进行的，同样没有考虑粗糙度的影响。本文在传统轴承动力学分析模型的基础上考虑了轴瓦的刚度、阻尼和轴承质量以及可能存在的接触刚度、阻尼，提出了水润滑轴承动力学特性分析模型。基于该模型推导了考虑表面粗糙度与轴瓦变形的扰动压力雷诺方程并计算水膜动力特性系数，对比了混合润滑模型与动力润滑模型、弹流润滑模型下轴承的动力特性系数并分析其差异，深入讨论了轴颈倾斜与粗糙度对水润滑轴承动力特性系数的影响。本文提出的模型与动力特性系数计算方法可完善柔性轴承-转子系统动力学分析。

1 数学模型

1.1 水润滑轴承动力学特性分析模型

传统轴承动力学分析模型适用于表面光滑的刚性轴承。但是，水的低粘度以及艉轴承低速重载的工况特点导致最小水膜厚度与表面粗糙度处于同一量级，此时表面粗糙度不仅影响实际水膜厚度，甚至可能彼此接触。除此以外，水润滑轴承采用非金属柔性轴瓦，轴颈稳定运转时，轴瓦将产生静态变形；当轴颈在轴承内涡动时，水膜压力的动态变化会导致轴瓦产生动态变形。为了表征以上特点，建立如图1所示的水润滑轴承动力学分析模型。

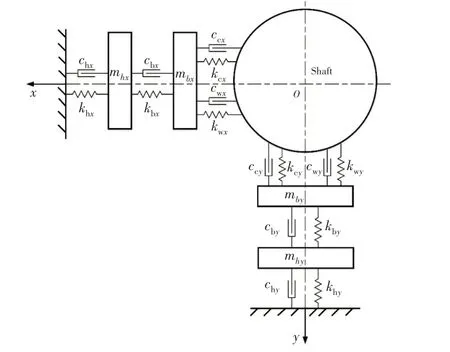
图1 水润滑轴承动力学分析模型Fig.1 Dynamic analysis model of water lubricated bearing

图1 中，下标x、y代表物理量的作用方向，kw、cw为水膜刚度、阻尼，kc、cc为粗糙峰接触刚度、阻尼[20]，kb、cb为轴瓦刚度、阻尼，kh、ch为船体基础刚度、阻尼，mb为轴承质量，mh为船体基础质量。图中未标出水膜的交叉刚度、阻尼。上文提及的水润滑轴承特点在图1 中体现如下：粗糙度的效果体现在两个方面，首先，在最小膜厚区域，粗糙度改变了水膜的真实厚度，会对水膜动力特性产生直接影响；其次，轴承、轴颈表面的粗糙峰彼此接触时，会产生接触刚度和阻尼。在轴瓦变形方面，静态变形可由轴承的稳态分析得到，动态变形则由轴承的二自由度集总参数模型表示。轴瓦的动态变形由水膜压力的动态增量引起，在图1 中由串联弹簧、阻尼表征这一受力-变形关系。此外，除了轴瓦刚度kb外，非金属材料的阻尼cb与轴瓦质量mb均被计入了模型。若船体基础的刚度和阻尼不可忽略，则可继续串联在模型中。

虽然该多自由度模型不能将轴承的动力特性通过简明的刚度和阻尼系数表示，但是粗糙度效应、轴瓦变形以及非金属轴瓦的刚度、阻尼与轴承质量均被纳入了轴承动力学分析模型，有利于提高柔性轴承支撑时轴系响应的预报精度。同时，该模型中水膜力增量与轴承座运动方程的表征并不复杂，易于组装至轴系动力学模型中。此外，轴瓦结构刚度、阻尼与水膜刚度、阻尼的串联，使水膜动力特性系数计算与轴瓦动态变形解耦，计算水膜刚度阻尼时只需考虑轴瓦静态变形，一定程序上简化了水膜动力特性系数的计算。

下文将重点讨论考虑轴瓦变形与表面粗糙度的水膜动力特性系数计算。

1.2 水膜动力特性系数理论分析方程

图2 所示为典型的水润滑轴承结构示意图。轴承中心为O，轴颈中心为Oj，两者存在偏心距e，轴颈以角速度Ω旋转。轴颈半径为r，轴承长度为L，轴瓦表面P点处的膜厚为h，u、v为P点在x、y方向的弹性变形。角度坐标Φ、φ满足Φ=φ+θ，θ为偏位角。Fx、Fy分别为x、y方向的轴承承载力，轴颈关于坐标轴的倾角θx、θy、θz满足右手法则。

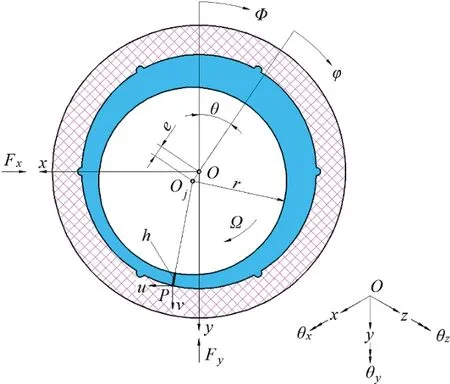
图2 水润滑轴承结构示意图Fig.2 Water lubrication bearing structure diagram

以轴承稳态的膜厚、水膜压力为基础求解动态特性系数。考虑粗糙峰对水膜压力的影响，本文采用考虑表面形貌的雷诺平均方程[21]描述水膜压力分布

式中，φx、φz为压力流量因子，φs为剪切流量因子，φc为接触因子[22]，为平均水膜压力，h为水膜厚度，μ为水的动力粘度，为综合粗糙度，σ1、σ2分别为表面1、2 粗糙峰高度的均方根，U1、U2分别为表面1、2 的速度。φx、φz、φs、φc的计算方法见文献[21-22]。假设粘度为常数，刚化轴承的静态变形，将式（1）无量纲化，得到

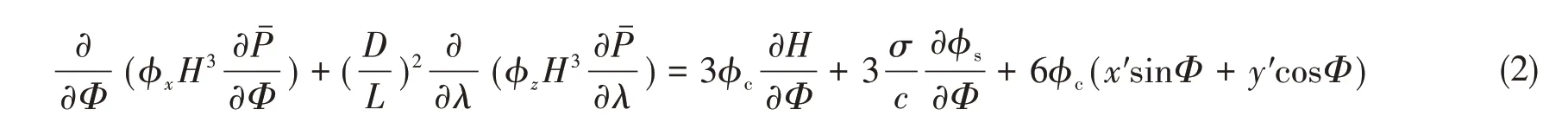
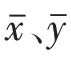
式中，H0为平衡位置的无量纲膜厚分布，δu为无量纲化的弹性变形导致的膜厚增量。

将水膜压力作泰勒展开，忽略2阶以上小量，得到

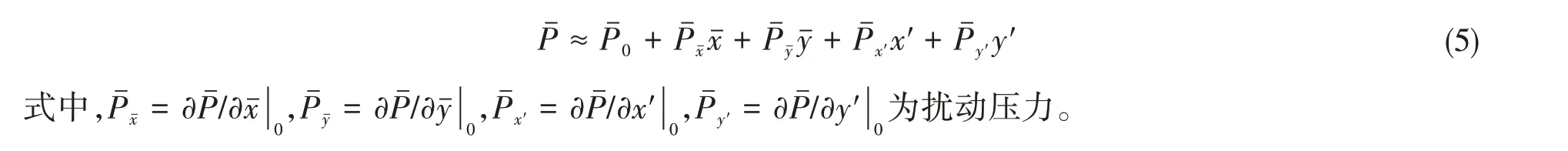
在平均流量模型中，粗糙度对水膜的影响由流量因子体现。为考察粗糙度对水膜刚度、阻尼的影响，流量因子也需要摄动展开。流量因子已被拟合为膜厚比h/σ的函数，保留线性项将流量因子作泰勒展开，得到

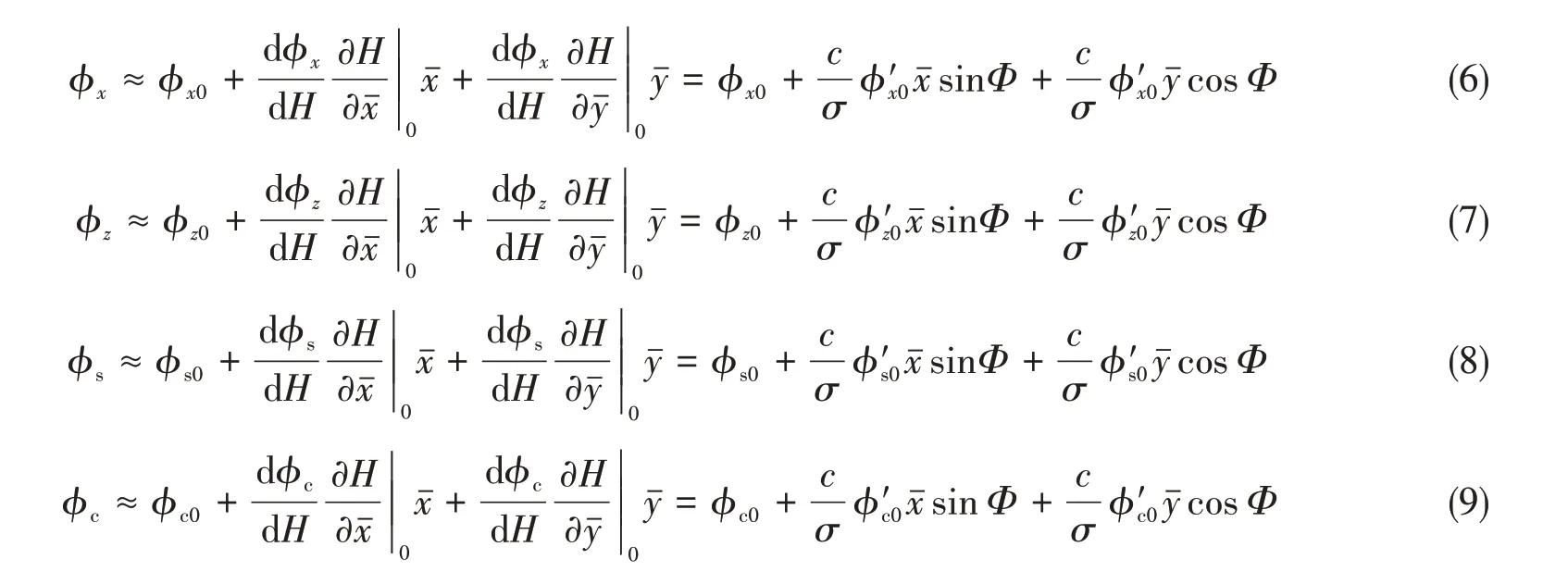
其中，流量因子关于扰动求导时应用链式法则，

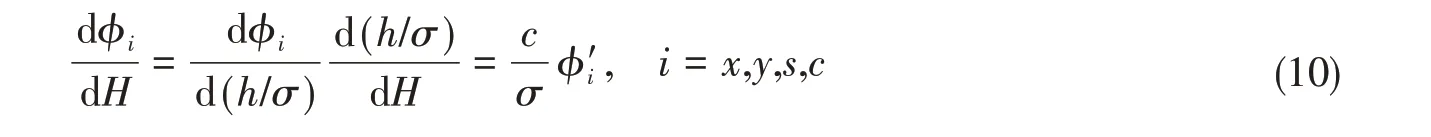
将式(3)、式(5)、式(6)-(9)代入式(2)进行整理，得到稳态雷诺方程和扰动压力雷诺方程

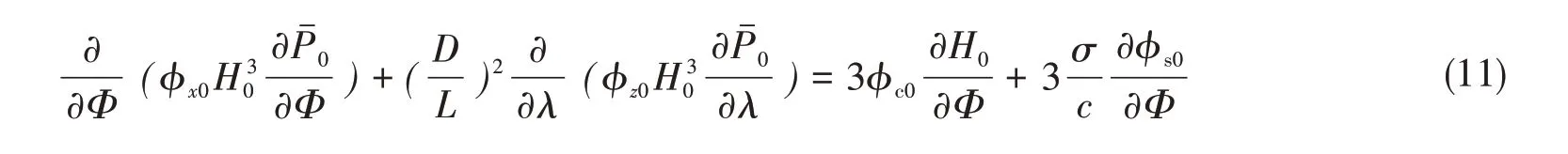
求解式（12）～（15），再对各扰动压力积分，得到无量纲水膜刚度、阻尼为

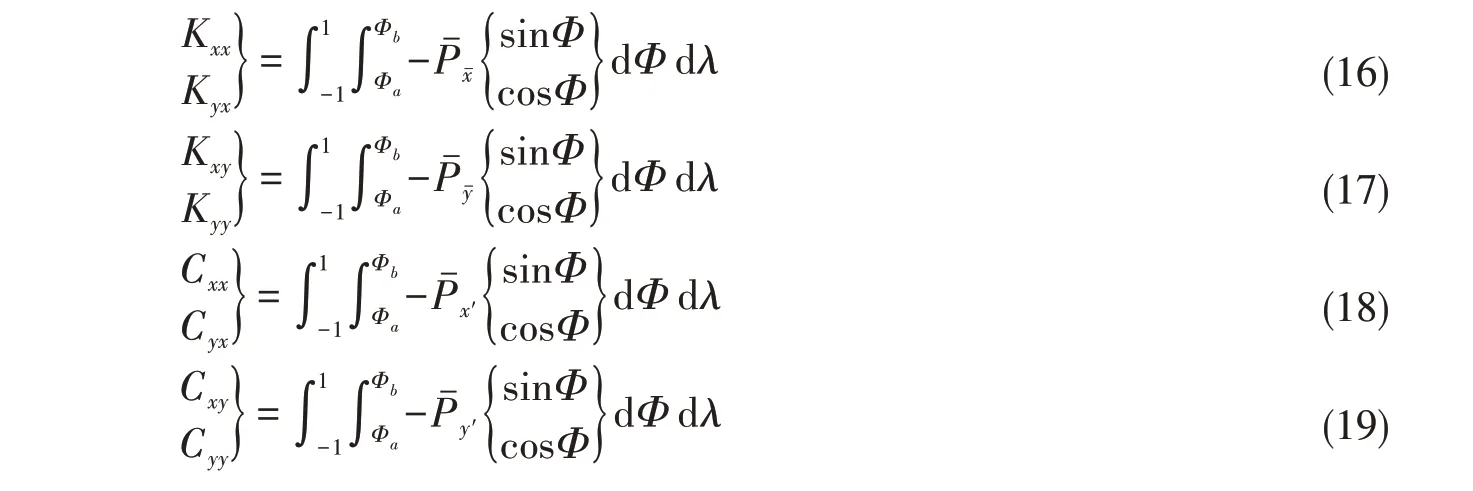
2 数值计算方法

本文采用有限差分法离散雷诺方程，以超松弛迭代法求解。采用20节点实体单元建立轴瓦的有限元模型计算轴瓦变形，粗糙峰接触采用弹塑性接触模型[20]。为简化计算，有限差分网格与有限元网格的节点一一对应，其网格协调关系如图3所示。

图3 有限差分网格与有限元网格的协调关系Fig.3 Coordination between finite difference grid and finite element grid

求解水润滑轴承动力特性系数的流程如图4所示。水润滑轴承主要由下瓦承载，本文对张角为150°的圆轴承下瓦，采用节点密度为65×65 的有限差分网格。经验算，该网格密度下的计算结果与更细密网格的计算结果相比，水膜刚度阻尼的相对变化极小。

图4 水润滑轴承动力特性系数计算流程图Fig.4 Flow chart of the calculation of dynamic characteristic coefficients of the water lubricated bearing

3 水润滑轴承动力特性系数计算

3.1 模型验证

小偏心率时轴瓦变形极其微小，且膜厚比h/σ≫4，轴承处于流体动力润滑状态。此时按照式（11）～（15）计算得到的动力特性系数应与动力润滑模型的计算值相同。本文以2×150°圆轴承为例（轴承参数见表1），与文献[1]中的标准值进行对比，结果如表2所示。

表1 验证模型轴承参数Tab.1 Parameters of the bearing for verification

表2 2×150°圆轴承无量纲水膜刚度、阻尼系数Tab.2 Dimensionless stiffness and damping coefficients of 2×150°circular bearing

续表2

对比可知，采用本文计算方法的动力特性系数值与标准值非常接近，验证了本文算法的正确性。

3.2 粗糙度与轴瓦变形对水膜动力特性系数的影响

为考察粗糙度与轴瓦变形对水膜动力特性系数的影响，设置4个算例如下：算例1，既考虑粗糙度也考虑轴瓦变形(混合润滑状态，ML)；算例2，仅考虑轴瓦变形(弹流润滑状态，EHL)；算例3，仅考虑粗糙度(刚性混合润滑状态，rigid ML)；算例4，既不考虑粗糙度也不考虑变形(动力润滑状态，HL)。轴承尺寸与工况参数如表3所示，分别计算偏心率为0.95与0.98两种工况下的动力特性系数，结果如图5-6所示。

表3 轴承参数Tab.3 Bearing parameters used in analysis(2×150°circular bearing)

首先对比算例2（EHL）和算例4（HL），分析变形对刚度阻尼的影响。由图5～6可知，偏心率为0.95时，弹流润滑状态下y方向的刚度系数小于动力润滑状态下的数值；随着偏心率增至0.98，弹流润滑状态下的动力特性系数明显小于动力润滑状态下的动力特性系数。这与前人的研究结论一致[6]：考虑了轴瓦弹性后，大偏心率下水膜厚度因轴瓦变形明显增大，导致了水膜刚度阻尼的减小。

图5 偏心率为0.95时动力特性系数随表面粗糙度的变化曲线Fig.5 Dynamic coefficients of water film versus surface roughness when ε=0.95

对比算例3（rigid ML）和算例4（HL），分析粗糙度对刚度阻尼的影响。表面粗糙度很小时，刚性混合润滑状态与动力润滑状态下的动力特性系数接近。在两种偏心率下，刚性混合润滑状态的刚度系数均随着粗糙度提高先增大后减小，但偏心率为0.98 时刚度峰值对应的粗糙度小于偏心率为0.95 时的对应值。偏心率为0.95时，刚性混合润滑状态下，cyy以外的阻尼系数随着粗糙度提高先增大后波动地减小；而偏心率为0.98时，cyy以外的阻尼系数随着粗糙度提高直接波动地减小。粗糙峰对kyy和cyy的增幅效果尤其显著：对kyy具有增幅作用的粗糙度范围大于其他刚度系数，cyy在两种偏心率下均随着粗糙度提高波动地增大。在平均流量模型中，粗糙度的影响由流量因子体现。粗糙峰高度的增加，会增大水膜的流动阻力，也减小了两表面间的实际水膜厚度，因此水膜刚度和阻尼随着粗糙度增大而增大。但是随着粗糙峰高度增加，最小膜厚比不断减小，当最小膜厚比小于某一阈值时，根据平均流量模型，粗糙峰高度继续增大会导致更多的粗糙峰彼此接触，减少表面间的通流面积与流量，流量因子将逐渐减小至0。所以粗糙峰对水膜刚度阻尼的增幅作用被流量减少所抵消，刚度阻尼随着粗糙度进一步增大而下降。此外，通过刚性混合润滑在2种偏心率下的动力特性系数对比可知，大偏心率或小间隙轴承对粗糙度更加敏感，因为此时粗糙度的增加更易使最小膜厚比低于增长阈值，致使水膜刚度阻尼减小。

对比算例1（ML）和算例3（rigid ML），分析粗糙度与轴瓦变形对刚度阻尼的综合影响。表面粗糙度很小时，混合润滑状态与弹流润滑状态下的动力特性系数接近。考虑变形后，水膜刚度、阻尼随粗糙度的变化类似于刚性混合润滑状态：在两种偏心率下，混合润滑状态的动力特性系数均随粗糙度提

高先增大后减小，且各刚度、阻尼系数峰值对应的粗糙度大于刚性混合润滑状态下的对应值。除此以外，混合润滑状态下y方向的刚度阻尼随粗糙度的增长率小于刚性混合润滑状态下的增长率，这在偏心率为0.98 时尤为明显。分别计算混合润滑与刚性混合润滑在刚度阻尼上升至峰值处的最小膜厚比，两种模型在刚度、阻尼峰值处的最小膜厚比较为接近。根据上述现象可知，引入轴瓦变形并没有彻底改变粗糙度对水膜刚度、阻尼的影响规律。由于变形增大了水膜厚度，相同的粗糙度下，混合润滑状态具有更大的最小膜厚比，相应地提高了最小膜厚比阈值对应的粗糙度。混合润滑状态下的阻尼系数依然能随粗糙度略有上升而不是直接下降，也是因为变形延迟了最小膜厚比阈值的到来。此外大偏心率下变形主要集中在承载的y方向，故y方向粗糙度对刚度、阻尼的增幅效果受水膜厚度增大影响而有所削弱。

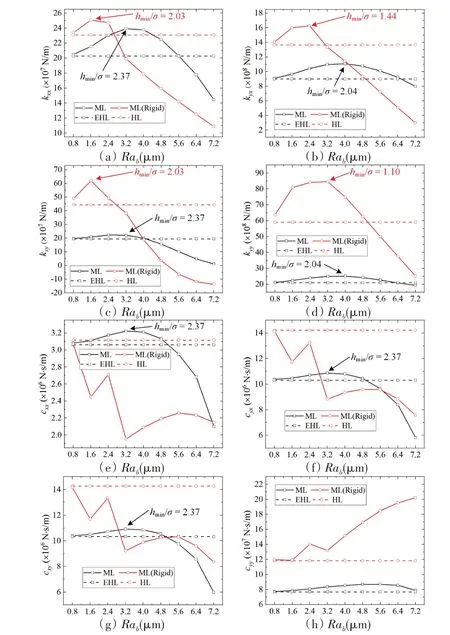
图6 偏心率为0.98时动力特性系数随表面粗糙度的变化曲线Fig.6 Dynamic coefficients of water film versus surface roughness when ε=0.98

3.3 倾角对水润滑轴承动力特性系数的影响

本节讨论轴颈倾斜对水润滑轴承动力特性系数的影响，轴承参数见表4。艉轴在螺旋桨重力作用下挠曲变形，导致轴颈在轴承中倾斜，影响水膜压力分布。本文计算轴颈发生纵向倾斜，即θx＞0 时的动力特性系数。设置不同的外加载荷与轴承表面粗糙度（包括轴承光滑的弹流模型）构成对比。

表4 轴承参数Tab.4 Bearing parameters used in the analysis(2×150°circular bearing)

图7～8 展示了不同载荷与粗糙度下动力特性系数随倾角θx的变化曲线。由图可知，在特定载荷与粗糙度下，水膜的刚度和阻尼系数随倾角的增大而增大，但kxy会在载荷和倾角较大时下降。此外，粗糙度对刚度和阻尼的影响规律相同。倾角较小时，各粗糙度以及光滑轴承的水膜刚度和阻尼十分接近，但是动力特性系数随倾角的增长率与表面粗糙度呈反比，当倾角较大时，粗糙轴承的刚度和阻尼明显小于光滑轴承的刚度和阻尼。上述现象在轴承载荷较大时更为明显。

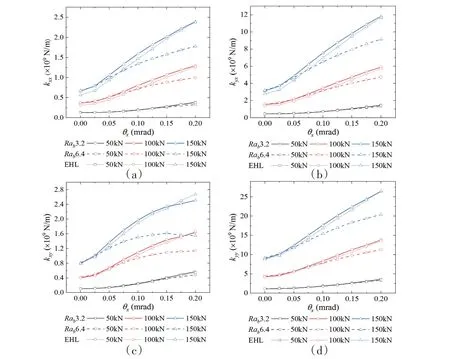
图7 刚度系数随倾角的变化曲线Fig.7 Stiffness coefficients versus misalignment angle

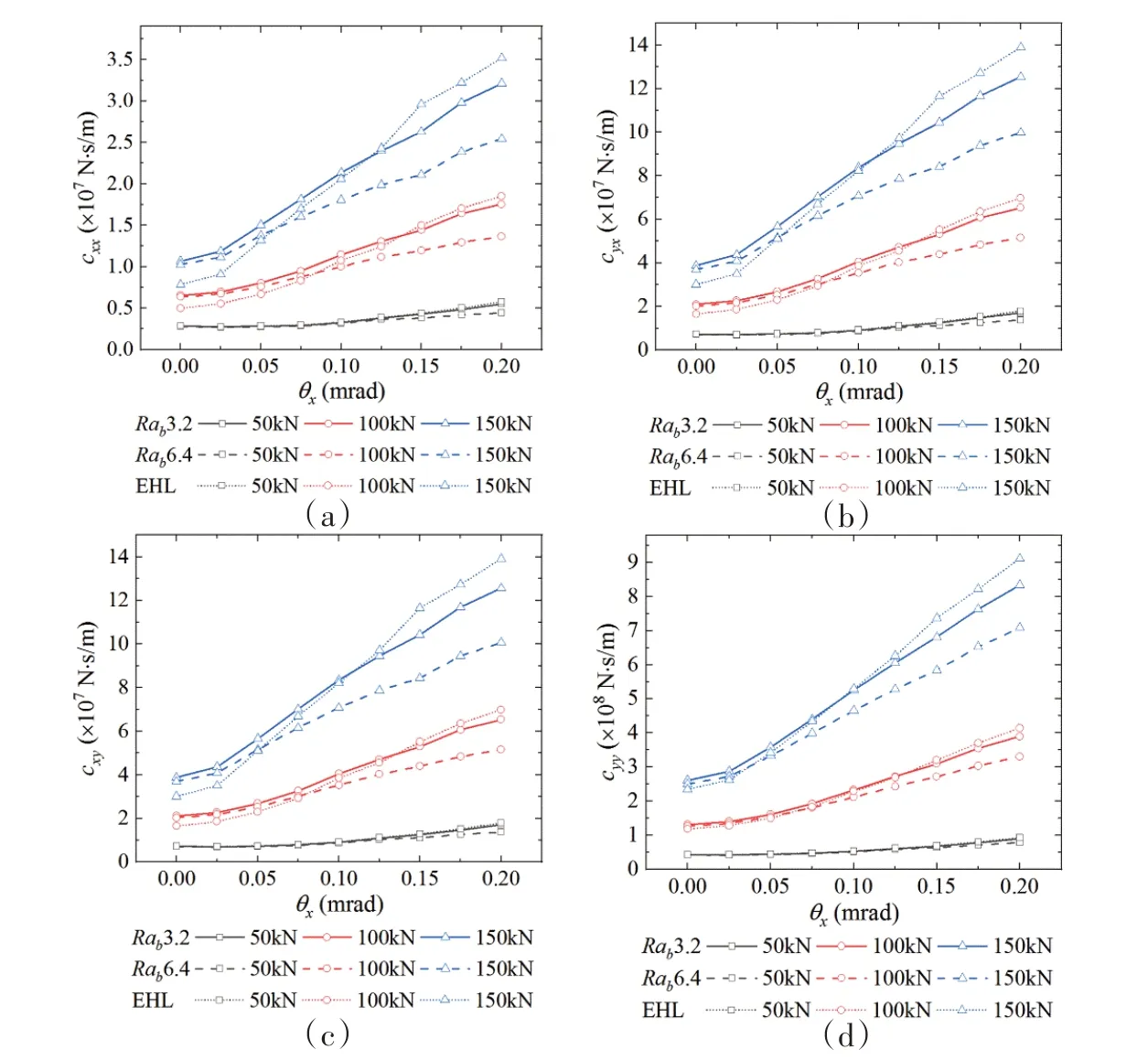
图8 阻尼系数随倾角的变化曲线Fig.8 Damping coefficients versus misalignment angle

为了解释上述规律，给出计算工况下各轴承的最小水膜厚度hmin随倾角的变化曲线，如图9所示。对外载荷一定的轴承，其最小水膜厚度随着倾角增大而减小，这是因为倾角增大后轴承必须运行在更大的偏心率下以弥补倾角增大造成的承载力损失。相应地，最小水膜厚度的减小会导致水膜刚度和阻尼的增大。此外，从图9中还能观察到固定载荷与倾角下，最小水膜厚度与粗糙度呈正比。并且，不同粗糙度间最小水膜厚度的差异随着倾角增大而增大，当倾角较大时，粗糙轴承的最小膜厚明显大于光滑轴承。Wang 等[5]曾经指出，粗糙度具有提高水膜承载力的作用。当倾角增大，主要承载区向轴颈下沉端移动。在倾角增大的过程中，逐渐收缩的承载区域以及越来越薄的水膜，让粗糙度在承载方面的作用愈发凸显——粗糙轴承能用更厚的水膜承载起相同的外载。因此，在固定外载作用下，当倾角较大时，粗糙轴承的水膜刚度阻尼更小。

图9 最小水膜厚度随倾角的变化曲线Fig.9 Minimum film thickness versus misalignment angle

4 结 论

本文在传统轴承动力学分析模型的基础上考虑了轴瓦刚度、阻尼和轴承质量以及可能存在的接触刚度和阻尼，提出了水润滑轴承动力学特性分析模型。基于该模型推导了计入轴瓦弹性变形与粗糙峰影响的扰动压力雷诺方程。通过在不同工况下求解该方程，得到以下结论：

（1）当最小膜厚比较大时，粗糙度提高能增大水膜刚度和阻尼；但是随着粗糙峰高度增加，最小膜厚度比不断减小，当最小膜厚比小于某一阈值时，粗糙度继续增大会导致刚度、阻尼下降。，由此可推知，大偏心率或小间隙轴承将会对粗糙度更加敏感，若此类轴承的表面粗糙度过大，很可能会引起水膜刚度和阻尼的下降。

（2）大偏心率下轴瓦变形会导致水膜刚度和阻尼减小，并且变形提高了最小膜厚比阈值对应的粗糙度，扩大了使水膜刚度和阻尼获得增幅的粗糙度范围，但是变形也削弱了承载方向粗糙度对刚度阻尼的增幅。

（3）承受固定载荷的轴承，轴颈倾角增大会导致水膜刚度和阻尼增大。同时，轴颈倾斜会强化表面粗糙度在承载方面的作用，粗糙轴承的水膜的刚度和阻尼在倾角较大时明显小于光滑轴承的刚度和阻尼。